Journal of Software Engineering and Applications
Vol. 5 No. 1 (2012) , Article ID: 16677 , 4 pages DOI:10.4236/jsea.2012.51007
A New Method Which Combines Arithmetic Coding with RLE for Lossless Image Compression
![]()
Sciences and Technologies of Image and Telecommunications Higher Institute of Biotechnology, Sfax, Tunisia.
Email: {karimabdelmoula2004, mas_atef}@yahoo.fr, medsalim.bouhlel@enis.rnu.tn
Received October 7th, 2011; revised November 10th, 2011; accepted November 25th, 2011
Keywords: Adaptive Arithmetic Coding; Static Arithmetic Coding; Arithmetic Coding; Lossless Compression Image; Run Length Encoding
ABSTRACT
This paper presents a new method of lossless image compression. An image is characterized by homogeneous parts. The bit planes, which are of high weight are characterized by sequences of 0 and 1 are successive encoded with RLE, whereas the other bit planes are encoded by the arithmetic coding (AC) (static or adaptive model). By combining an AC (adaptive or static) with the RLE, a high degree of adaptation and compression efficiency is achieved. The proposed method is compared to both static and adaptive model. Experimental results, based on a set of 12 gray-level images, demonstrate that the proposed scheme gives mean compression ratio that are higher those compared to the conventional arithmetic encoders.
1. Introduction
The need for data compression is growing day by day because of the fast development of data intensive applications that place a heavy demand on information storage and to meet the high data rate requirements of bandwidth transmission systems such as multimedia [1].
Compression is the coding of the data to minimize their representation by removing the redundancy present in them, keeping only sufficient information that can be effectively used in the decompressing phase to reconstruct the original data. The compression of images is motivated by the economic and logistic needs to conserve space in storage media and save bandwidth in communication.
AC is the most powerful technique for statiscal lossless encoding that has attracted much attention in the recent years. It provides more flexibility and better efficiency than the celebrated Huffman coding does [2].
[3] AC has been widely used as an efficient compression algorithm in the new standards such JPIG2, JPEG 2000 [4] and H.264/AVC [5]. In [6] Howard et al. give a new paradigm of lossless image compression, with four modular components: pixel sequence, prediction, error modeling and coding. In [7], HOWARD et al. showed that high-resolution images can be encoded and decoded efficiently in parallel. They present an algorithm based on the hierarchical MLP method used either with Huffman coding or with a new variant of AC called quasiarithmetic coding. The coding step can be parallelized even though the codes for different pixels are of different lengths. Parallelization of prediction and error modeling components is straightforward. In [8], CARPENTIERI presents a new lossless image compression algorithm based on AC. The algorithm proposed appropriately selects, for each pixel position, one of a large number of possible, dynamic, probability distributions, and encodes the current pixel prediction error by using this distribution as a model of the arithmetic encoder. In [2], HAI et al. presents a new implementation of bit-level arithmetic coding by the use of integer additions and shifts. The new algorithm has less computation complexity and is more flexible to use, and thus is very suitable for software and hardware design.
In addition, the concept RLE used to record the number of repeating bits is applied for simplicity and efficiency.
In this paper, we propose a new method of lossless image compression based on combining AC with the RLE. The proposed method is compared to both static and adaptive model.
The rest of this paper is organized as follows. In Section 2, we briefly discuss the AC. Section 3 presents the RLE encoding technique. In Section 4, we describe the proposed method for lossless image compression. In Section 5, we discuss the experiments and the results. Finally, the conclusion of this paper will be discussed in Section 6.
2. Overview of AC
AC [9-12] is a statistical coder and it very efficient for data compression. In addition, AC has been widely used in many standards including JPEG2000, JPIG2 and H. 264/AVC.
The aim of AC is to define a method that provides code words with an ideal length. Like for every other entropy coder, it is required to know the probability for the appearance of the individual symbols.
AC is the most efficient method to code symbols according to the probability of their occurrence. The average code length is very close to the possible minimum given by information theory.
The AC assigns an interval to each symbol whose size reflects the probability for the appearance of this symbol. The code word of a symbol is an arbitrary rational number belonging to the corresponding interval.
The entire set of data is represented by a rational number, which is always placed within the interval of each symbol. With data being added, the number of significant digits rises continuously.
The principle of AC is the input stream. It is read symbol by symbol and appends more to the code each time a symbol is input and processed. To understand this method it is useful to imagine the resulting code as a number in the range (0, 1) that is the range of real numbers from 0 to 1 not including one. The first step is to calculate or at least estimate the frequency of occurrence of each symbol.
3. Overview of RLE
Most bitmap file formats such as TIFF, BMP and PCX use RLE as a data compression algorithm. It was created to compress any type of data regardless of the information it contains.
While this method is of little interest for compressing ordinary text, it can be a surprisingly effective for compressing binary images or low levels, containing little information, or with a disproportion of white/black pixels.
In addition it has excellent performance where a concentration of energy of the image is made. The RLE technique here is simply to describe the image line by line or column by column, by encoding only the tracks of constant color.
RLE is one of the oldest, the simplest and most used methods. Its whole secret is to identify and eliminate redundancies in the encoding of information in a more compact form.
Its principle is based on counting the number of identical patterns in the data range studied and is used to reduce the physical size of a repetition of string. This repeated string called passage is thus typically encoded into two parts. The first which is the number of repetitions, is called the counter and the second is the value of the passage.
A new packet is generated whenever the character changes or the number of characters exceeds the maximum value of the counter. Thus, the more the patterns are repeated, the better the results are.
RLE is used in image compression either as a standalone tool or as an element of a larger processing chain. Compressing an image using RLE is based on the observation that if we select a pixel in the image at random, there is a good chance that the neighbors of the pixel will have the same intensity value. This is particularly true for binary images. For grayscale and color images, RLE is normally used following the transform and quantization step.
The idea behind the RLE is that if a data item d occurs at n consecutive times in the input stream, compression can be achieved by replacing the n occurrences with the single pair nd. The n denotes the number of consecutive occurrences or the run length of data item d, thus the name run length encoding.
The Figure 1 presents an example of RLE compression.
4. Proposed Method
Figure 2 shows a new method which combines arithmetic coding with RLE for lossless image compression.
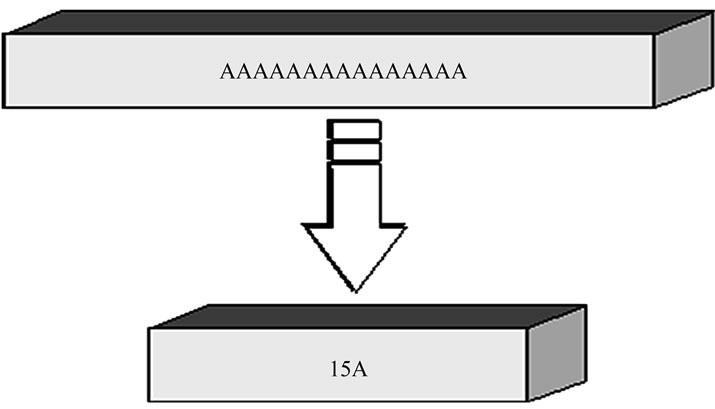
Figure 1. Example of RLE compression.
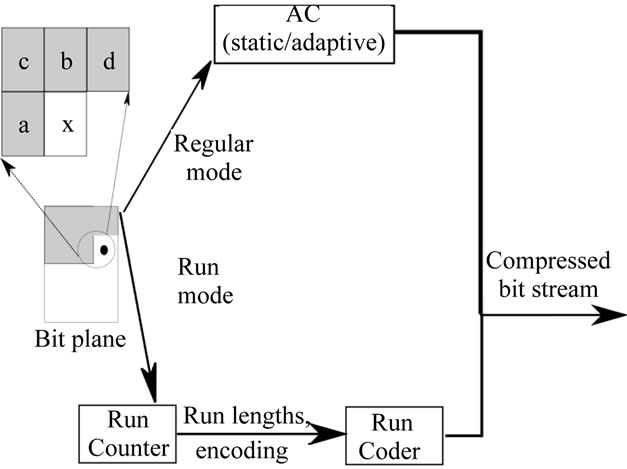
Figure 2. Our approach: Block diagram.
The algorithm of this approach is to apply the following operations:
1) Decompose the image into blocks of pixels.
2) Apply the algorithm encoding of a single component.
Next we apply the following steps for encoding of a single component.
Step 0. Initialization:
1) Encode the first line with AC (static or Adaptive);
2) Initialize to 0 the number of repetition;
3) Set current sample x to the first sample in the image.
Step 1. Compute the “local gradients” g1 = a - c, g2 = c - b, g3 = b - d.
Step 2. If g1 = g2 = g3 = 0, go to “run” mode processing.
Otherwise, continue in “regular” mode.
Step 3. Go to Step 1 to process the next sample.
The run mode processing steps are summarized in:
Step 1. Read the new samples until either x ≠ a or the end of the line is encountered.
Step 2. If the run was interrupted by the end of a line, append the value of a and the number of repetitions to the output stream and go to Step 1 of the main algorithm. Otherwise, increment the number of repetitions.
From the images presented in Figure 3 we can see that in the bit plane number 4 (Figure 3 (g)) the image contains noise and the number of consecutive sequences of 0 and 1 decreases.
Based on what is shown in (Figure 3), from bit plane 4, the number of homogeneous areas decreases and there is a lot of noise. In the case of this reduction, we have nothing to gain either with AC or with a combination of RLE with the AC.
For this purpose in the experiment result, we just use our approach to compress the bit planes 7, 6 and 5 while the other bit planes are not compressed because nothing is gained.
The repeated count given by the RLE is encoded on 8 bits because tests have shown that when using a number above or below 8 there is nothing to be gained because the file size will always increase.
5. Experiment Result
In this section, we discuss the results the of image compression by combining the AC with the RLE. Indeed, to validate our approach, we compared it with the AC (static and adaptive model), in terms of compression. However, all the results in this paper are presented using a test set of 12 images [13], demonstrate that the proposed scheme gives mean compression ratio that are higher those compared to the conventional arithmetic encoders.
The varying size of the images is chosen for the validation of our approach. All the images are grayscale (8 bits/pixel).
 (a)
(a) (b)
(b) (c)
(c) (d)
(d) (e)
(e) (f)
(f) (g)
(g) (h)
(h)
Figure 3. Lena bit plane: (a) Lena bit plane 7; (b) Lena bit plane 6; (c) Lena bit plane 5; (d) Lena bit plane 4; (e) Lena bit plane 3; (f) Lena bit plane 2; (g) Lena bit plane 1; (h) Lena bit plane 0.
The results in Table 1 contain both the entropies after the compression ratio calculated as a ratio between the size of the files containing the original image and the compressed image.
The compression ratio is defined by:

The compression ratio is calculated by dividing the size of the original image by the size of the compressed file.
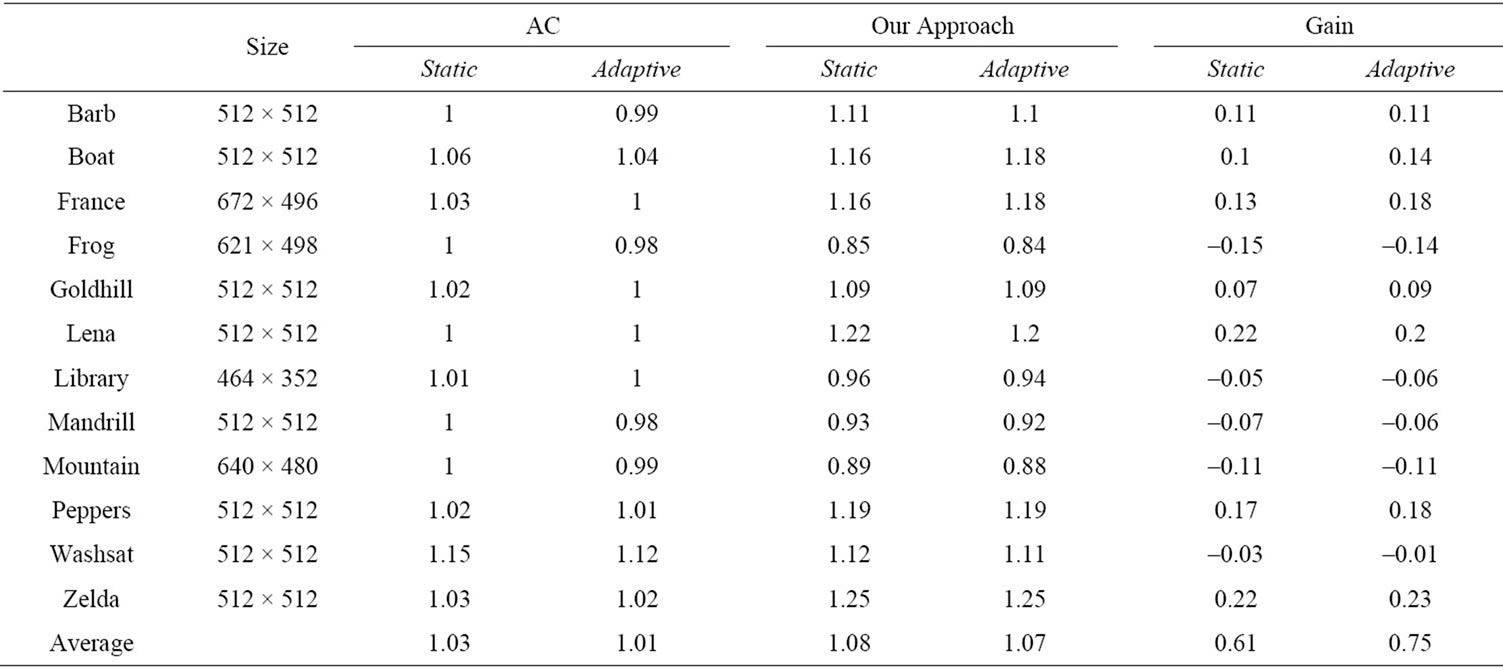
Table 1. The compression ratios of the 12 images.
6. Conclusion
In this paper, we proposed a lossless image compression algorithm based on the combination of the AC with the RLE. In our algorithm, we exploit both the efficiency of the RLE in lossless image compression and the advantages of the AC with its two models (Static an Adaptive) to provide an algorithm which can be very useful in many applications such as medical imaging.
REFERENCES
- S. Mahapatra, J. L. Nunez, C. Feregrino and S. Jones, “Parallel Implementation of a Multialphabet Arithmetic Coding Algorithm,” IEE Colloquium on Data Compression: Methods and Implementations, IEE Savoy Place, London, November 1999, pp. 91-95.
- M. Hai, J. Zhang and X. Ni, “An Improved Arithmetic Coding Algorithm,” Journal of Shanghai University (English Edition), Vol. 8, No. 4, 2004, pp. 455-457. doi:10.1007/s11741-004-0056-9
- A. Masmoudi, W. Puech and M. S. Bouhlel, “A New Joint Lossless Compression and Encryption Scheme Combining a Binary Arithmetic Coding with a Pseudo Random Bit Generator,” International Journal of Computer Science & Information Security, Vol. 8, No. 1, 2010, pp. 170-175.
- ISO/IEC FCD 15444-1, JPEG2000 Image Compression Standard, 1999.
- Joint Video Team JVT of ISO/IEC MPEG and ITU-T VCEG, Joint Committee Draft (CD), May 2002.
- P. G. Howard and J. S. Vitter, “New Methods for Lossless Image Compression Using Arithmetic Coding,” Information Processing & Management, Vol. 28, No. 6, 1992, pp. 765-779.
- P. G. Howard and J. S. Vitter, “Parallel Lossless Image Compression Using Huffman and Arithmetic Coding,” Information Processing Letters, Vol. 59, No. 2, 1996, pp. 65-73. doi:10.1016/0020-0190(96)00090-7
- B. Carpentieri, “A New Lossless Image Compression Algorithm Based on Arithmetic Coding,” Lecture Notes in Computer Science, Vol. 13, No. 11, 1997, pp. 54-61. doi:10.1007/3-540-63508-4_105
- P. G. Howard and J. S. Vitter, “Arithmetic Coding for Data Compression,” Proceedings of the IEEE, Vol. 82, No. 6, 1994, pp. 857-865. doi:10.1109/5.286189
- G. G. Langdon, “An Introduction to Arithmetic Coding,” IBM Journal of Research and Development, Vol. 28, No. 2, 1984, pp. 135-149. doi:10.1147/rd.282.0135
- A. Moffat, R. M. Neal and I. H. Witten, “Arithmetic Coding Revisited,” ACM Transactions on Information Systems, Vol. 16, No. 3, 1998, pp. 256-294.
- I. H. Witten, R. M. Neal and J. G. Cleary, “Arithmetic Coding for Data Compression,” Communications of the ACM, Vol. 30, No. 6, 1987, pp. 520-540.
- “The Waterloo Fractal Compression Project. Waterloo Repertoire Grey Set 2,” University of Waterloo, Ontario. http://links.uwaterloo.ca/Repository.html

