Journal of Service Science and Management
Vol.08 No.04(2015), Article ID:58690,9 pages
10.4236/jssm.2015.84053
Fore Sighting and Estimating the Risk of Investing in the Construction of Power Plants Using AHP
Shayan Hosseini1, Gevork Gharehpetian2, Fereshteh Farzianpour3*
1Electrical Engineering School, Amirkabir University of Technology, Tehran, Iran
2Iran Grid Secure Operation Research, Amirkabir University of Technology, Tehran, Iran
3Department of Health Management and Health Economics, School of Public Health, Tehran University of Medical Sciences, Tehran, Iran
Email: riercom@yahoo.com, grptian@aut.ac.ir, *farzianp@sina.tums.ac.ir
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 24 June 2015; accepted 7 August 2015; published 10 August 2015
ABSTRACT
Today, with advances that have occurred in electricity industry and technology of manufacturing all kinds of power plants whether renewable or perishable, making decision to choose the type and kind of an ideal plant is very important and strategic. For any weakness in determining short, medium and long term parameters affecting deciding whether technical, economical, environmental, social, political , and so on may cause irreparable damage. Also timing and fore sighting factors should be taken into account in decision-making equations. Selecting the type suitable for use in power plants connected to the network or independent sector is the main part of task. Therefore, because there are many variables and factors in the text and the margin of such a task, bed and plant kind selection is very difficult and time consuming. This choice is ultimately influenced by many technical and non-technical measures that are each divided into further subcategories. Due to repetition of this operation in the discussion of issues, finding an efficient way in this area would be very useful. In this paper, a hierarchical decision-making procedure for the selection of the ideal power for productivity and satisfaction in the operation of taking is introduced. That can be generalized to other types of construction and operation concepts in technologies of power plants.
Keywords:
Fore Sighting, Risk Estimation, Construction of Power Plants, AHP

1. Introduction
If one or a series of investments believe that a power plant during its lifetime benefit for facilities will invest for facilities and devices of production [1] . More specifically, benefit from the plant should be more than the cost of construction and operation of power plants; of course by taking into account environmental, political economy and other peripheral factors in building that power plant which are considered little in calculations of building power plant or are not considered at all, so that these parameters can easily be ignored [2] ; while these apparently insignificant points may appear gradually after opening of a plant and finally, we conclude that such environmental harm or political geography harm of building of a plant may be more than the benefits of electricity produced by that plant if other technologies used to produce electricity at the plant would be better and greater benefits to be achieved and we are less affected of some of those aspects [3] . In addition, this benefit should be more than the benefit that investor is achieved from other economic activities with similar risk level [4] . In this paper, we assume that to power the new power plant connected to the grid or stand-alone or network is our basic requirements [5] . The plant can be designed in a large or small scale production or in the form of distributed generation which will provide the electricity needs of consumers. Then after describing the literature of topic, we will describe the way of calculating, estimating and comparing the weight of investment risk to build different power plants to do this. We use the technique of hierarchical decision or AHP [6] - [10] .
2. Literature Review
The decision to invest in new power plant the investor should calculate all the long term marginal costs and the price of electricity in the plant may be sold to predict [6] . Until the predicted price is more than the long term marginal price of plant building a plant is logical [11] . In an open electricity market this logic can be used to invest in production capacity [12] . Relying on this type of decision leads to what is called commercial development [13] . It is important to note that the use of distributed generation and plant construction Power plant construction right near the consumer in cases is unvoiced [14] . For example, in remote areas away from the power grid or where the power consumption is small and electrical transmission lines and power losses due to the cost of the cable is irrational [15] . Decision about what distributed generation technology should be used is so important [16] . In practice, the decision about investing in a new production plant is considerably more complicated than what the theory suggests. In fact, both sides of the equation are affected by the considerable amount of uncertainty [17] . For example, delays in construction and fluctuations in the price of fossil fuel power plants or swinging in the wind and sun and using storage devises in renewable energy power plants on the other hand can affect long-term marginal costs [18] . In more sensitive cases reliability topic and use of reserve capacity and power quality issue is also considered [19] . On the other hand, manifestly forecasting gradual changes in whole- sale electricity prices in a long period of time is difficult, because demand may change, competitors may enter the market or new efficient technologies for production may be developed [20] . Development of commercial plants is often only possible when supported by main and secondary contracts [21] . In fossil fuel power plant main contracts guarantee Supply of fuel at a fixed price, that renewable power plants are exempt of it [22] [23] . Subcontracts guarantee that energy produced by power plant to sell at a price which is fixed [6] . Such agreements price risk is often very little controlled by the owner of power plant so they are eliminated [7] . Thus, the owner of power plant is undergoing the risk associated with the operation of the power plant [10] . A production power plant like any other machine is designed for optimal performance in specific years. Investors that decide to build a production power plant make their decisions based on an estimate of lifetime. Typically for power plant this lifetime is changed from 20 to 40 years [24] . Nevertheless as an example some of the hydropower plants considerably live longer [25] . To use the perspective of a potential investor factors that are useful in building a new production power plants are considered. The failure of existing power plants when they are insufficient profitability should be considered. About provision of production capacity from the perspective of consumers, it should be noted that such a major role in the economic activity of electricity for industrial and personal welfare of the community that consumers are demanding system that guarantee a reliable supply of electrical energy. Consumers expect the power supply not only when demand is not subject to fluctuation but when some generators or productive resources due to technical issues are also available and inexpensive to produce [26] [27] . Hence, it should consider that whether profits from the sale of electric energy the total production capacity available to meet consumer expectations arises is whether sufficient or not? Since the answer is negative in many of the electricity markets. Be sure obligation or incentive bonus and other added value should be considered that encourage manufacturing companies or individuals who are able to provide the necessary capacity needed to community [23] .
3. Fore Sighting in Selection of Power Plants for Manufacturing
In selection of suitable power plants for the manufacture many factors are involved [7] . These include factors such as technical and non-technical as economic, time, environmental, social and political again, each of which is divided into smaller elements, as an example to build a power plant about the environmental factors can be said that; which arise the following factors, soil contamination, weather and as well as the effects of power plant construction is an important challenge in regional climate change on ecosystems and organisms that live in the region which can referred to either visual or noise pollution and or being a power plant in the migration of birds and other animal species [26] [27] . As you can see there are many minor factors to study. However sometimes these minor factors magnification over the time. As an example in design and selection we should not forget wildlife and nature. Summary selection of suitable power plants to build and exploit it depends on so many factors and these dependences and unknown and variables make decision making process difficult. The most important things to know about the type of power plant to construct and justify the need to build it view as geographical proximity or remoteness of the construction of the national power grid to connect to the local network or the use of power plants for use in either of distributed generation will noted (Table 1) [28] -[30] .
The next steps in parallel, technical and economic factors entered the field of elected, what type of technology and the capacity should be used to build power plants and that cover which amount of the initial investment and the rate of return on technology investments Technology of construction of primary energy consists of two categories:
A. Fossil fuel power plants or mortal
B. Renewable Power plants
That each spectrum has its own advantages, disadvantages and threats and must analysis any particular geographic location. Factors and other parameters exist that may at first glance to be less valuable than technical and economic factors that can confirm or deny construction of a power plant that we called all the effective factors in construction of a power plant in the first row of Table 1 It includes the following: Geographical location: influences of climate and weather conditions, Technical: having technical science, complexity of the technology used to obtain power quality, Economic: availability of fuel. Fuel prices [28] -[30] .
The total cost of materials Equipment and setup. As well as maintenance and ground, Time: time to build, time startup or coming into orbit, useful life. Administrative: Office personnel to build, repair and maintenance. Environment: soil pollution, water, air, audio etc. Social and cultural rights: a positive impact on productivity, Political: sanctions and the arrival of new technologies, Cultural and natural heritage: damage, the area of land required, structural architecture: design art, finally, the tourism: a positive impact on an attraction. Although there are more details to mention that we betake to say them in this article, they are also listed in the first column of the table types of power plants. Within this table, we consider general and absolute technical and non-tech- nical specifications and feature a variety of power plants intended for construction. It should be noted that this table default and theoretical and complete expert system given the expertise is changeable and generalized. As you can see in this table numerical parameters are not faced with symmetric error but with a complex and heterogeneous asymmetric other highly nonlinear time-varying weights have been exposed to human factors were also strongly affected, So there is no escaping that we have to decide and choose the most efficient plant for the manufacture of any particular geographical area MADM techniques to take advantage of these issues [23] .
3.1. Providing AHP Solutions in Order to Make Decisions and Choices
In the construction and operation of all types of power plants due to exposure to various factors, there are many variables affecting the decision and the choice is difficult. In this selection there is technical and non-technical problem and they are often impossible to be collected [16] . The best way is using a scientific and practical decision-making practices. In this regard, it seems hierarchical cluster analysis approach (AHP) is the best option available. AHP’s approach to decision making is to choose one among several similar cases according to various criteria. In other words, it is a multi-criteria decision making [17] . Criteria can be listed as a separate division. Most of the time, it can be interpreted so that the number of main criteria and then in the main criteria are several other criteria. How to use the AHP can be summarized as follows:
Table 1. General and absolute description of technical and non-technical characteristics of different types of power plants for building.
1) Modeling of an issue as a hierarchical system that has the specific objective.
2) Prioritized on the basis of some of the judgments of the ranking is done by comparing two binary.
3) This judgment is combined with a set of priorities for ranking achieved.
4) The harmony of judgments is evaluate.
5) According to the process done final result was obtained (Figure 1).
So the structure and algorithm like what is shown in picture number one is obtained [19] . Select the type of power plant for construction and operation establishment and implementation of a hierarchical structure in Figure 2 is suggested, since taking into account all the circumstances leading to better results. The criteria are divided into two categories: technical and non technical measures. It has all the aspects to be considered. These two main criteria as shown in picture number 2 are divided to minor criteria. The model is shown in Figure 2. Each power plant is evaluated according to its all criteria. Furthermore, each station through its main criteria is measured by the standards of most technical or non-technical.
3.2. Evaluation Tables
After identifying the criteria, different types of power plants are rated against a specific criterion. In this context, a table like Table 2 is produced for each criterion then the tables are given to statistics expert group of professionals and experienced researchers in this area. Till each of them rate, weight and do paired comparison according to Table 3, Some measures, such as costs are quantitative and do not need for paired comparison. It should be noted that in the weighting table whatever the cost is less higher scores are given to those options. And their class ranking can be achieved. But other criteria that are qualitative or are combination of qualitative and quantitative should be analyzed by an expert system and also be paired comparisons, as an example to prepare the annual cost of a thermal power plant can use the following formula: E × H × F = Annual production costs.
Which E is equal to the estimated annual production based on MWh, H = Heat rate at rated output based on Btu\kWh, F = fuel expected cost based on Mbtu. Which can be said about E: E = Coefficient of utilization\MW nominal capacity of the plant × 8760 hour\year.
It should be said about the estimated annual, it is expected that ideally power plant should be worn at all times with full capacity utilization. In practice it is not possible, because power plant is shut down periodically for maintenance, also, errors inevitably arise which will lead to unscheduled exit, so In relation to E ,thus exploiting coefficient which is a number less than 100% should be used [30] . After weighting each of power plant in relation to each other and a specific criterion, now criterion should be weighted and compared in relation to themselves, to determine how much each of the criteria are worth. To do this table like Table 4 is designed and given to the previous expert and statistic group, till Table 3 does the weighting. After scoring and paired comparison matrix for the criteria its turn for math calculation the values should be changed to the norm tables, to this must
Figure 1. Formulated structure and algorithm of hierarchical decision making process (AHP).
Figure 2. Hierarchial diagram proposed for selecting kind of power plant for construction.
Table 2. Comparison of different types of power plants to a specific criterion.
Criterion 1.
Table 3. Definition of devoted weights in comparison (AHP scale).
When the element I is compared with j one of the above numbers will be assigned to it. also in comparison I with j reverse number will be assigned (xji = \1 xij) and also all diagonal elements of this matrix is the number one.
Table 4. Comparison of different criteria to measure the upstream.
Technical and non-technical criteria or other criteria.
be for all tables the number in each column should be divided to the total of that column and then calculate the arithmetic mean of each row of the table.
With this work for any of a variety of plants, to the specific criteria, one number is get. This number is the number obtained by performing the same operation on the table. Values are multiplied. Then, for each type of power plant to have a number of different criteria, that the total numbers indicate the final weight of power plants, and this final weight will be the base for the final decision making about selected power plant to construction and operation, However, after evaluating the inconsistency rate that during the following 5 steps will be calculated.
3.3. Steps Measurement Inconsistency Rate
Step 1. Obtain the total weight (WSV): The relative weights of the vector obtained by multiplying a matrix of paired comparisons: WSV = D × W.
Step 2. Obtain the compatibility (CV): Divided by the weighted sum of the vector components of the vector of relative weights are obtained.
Step3. Calculation of the largest matrix of paired comparisons (max): The adjustment is calculated from the mean vector elements.
Step 4: calculation of inconsistency Index (II): Is given by the formula:
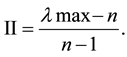
Step 5: calculation of inconsistency price (IR): Is given by the formula:
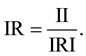
Here IRI (Random inconsistency index) is the value that is get from Table 5. The values of this table is based on the simulation of a large number of paired comparison n\n matrices obtained [8] .
If the inconsistency rate is less than or equal with 0.10 (IR 0.10); in paired comparisons there are consistent you can continue to work or decision-maker should review the paired comparisons.
Among other points that should be considered very, is the managers overall strategy. As an example If the overall goal is to minimize the annual and periodic costs of power plants instead initial investment has no restriction, can have a dramatic effect on the rate and also in contrast to the case and the factors influencing the selection process and decisions of senior managers to type of power plants it is true [8] .
4. Conclusion
Making decision for choosing the best option of power plant, for construction and exploitation, is one of the most important steps in efficiency of and reform of consumption pattern of primary sources in the production, that is also very important and plays a vital role in achieving national smart grid and in order to reach maximum functionality and realize existing potentials (beginning from extraction of primary resources to the targeted use and productivity). As it is seen in the present paper, lots of points and criteria should be considered for choosing power plant, that often or sometimes they cannot be gathered together. In this regard, a clear framework for selecting the type of power plant is very important and useful. It should be noted that the mentioned factors and criteria in this article can be extended to other criteria in this way there is no limit. The mathematical calculation method which is presented in this paper is based on an average and it can be generalized to other methods that each article has its own demands such as: eigenvectors, least squares, logarithmic least squares, rows or weighted least squares geometric mean. In addition, it should be noted that expert group and statistics that weight the tables and the final result is obtained through comparison of their weighting, they are one of the most important parts of the job and better results will be obtain if experienced experts are selected and brainstorm and think tanks are formed. Finally, the last point is determining the overall strategy of managers and announcing it to the experts who rate is so important and it would be better that the managers themselves are also specialists and experts and have the overall view of SWOT (strength, weaknesses, opportunities and threats) analysis of problem.
Table 5. Random inconsistency index (IRI).
Acknowledgements
This research was a part of the Ph.D. Research of the first author, conducted in senior research expert in elec- trical energy engineering, Power Technology Development Center. The authors would like to thank all participants in this research, particularly key informants and managers who participated in the research.
Competing Interests
The authors declare that they have no competing interests that may be perceived to influence the results and discussion reported in this manuscript.
Cite this paper
ShayanHosseini,GevorkGharehpetian,FereshtehFarzianpour, (2015) Fore Sighting and Estimating the Risk of Investing in the Construction of Power Plants Using AHP. Journal of Service Science and Management,08,526-535. doi: 10.4236/jssm.2015.84053
References
- 1. Kahraman, C. (2015) Fuzzy Multi-Criteria Decision-Making: Theory and Applications with Recent Developments. Semay Danesh Press, Tehran, 86-103
- 2. AKKOÇ, S. and Vatansever, K. (2013) Fuzzy Performance Evaluation with AHP and TOPSIS Methods: Evidence from Turkish Banking Sector after the Global Financial Crisis. Eurasian Journal of Business and Economics, 6, 53-74.
- 3. Avazpour, R., Ebrahimi, E. and Fathi, M.R. (2013) A 360 Degree Feedback Model for Performance Appraisal Based on Fuzzy AHP and TOPSIS. International Journal of Economy, Management and Social Sciences, 2, 969-976.
- 4. Deng, H. (1999) Multi-Criteria Analysis with Fuzzy Pair-Wise Comparison. International Journal of Approximate Reasoning, 21, 215-231.
- 5. Fang, C.H., Chang, S.T. and Chen, G.L. (2010) Competency Development among Taiwanese Healthcare Middle Manager: A Test of the AHP Approach. African Journal of Business Management, 4, 2845-2855.
- 6. Kirschen, D.S. and Strbac, G. (2004) Fundamentals of Power System Economics. c, 101-286.
http://dx.doi.org/10.1002/0470020598 - 7. Melón, M.G., Beltran, P.A. and Cruz, M.C.G. (2008) An AHP Based Evaluation Procedure for Innovative Educational Projects: A Faceto-Face vs. Computer-Mediated Case Study. Omega, 36, 754-765.
http://dx.doi.org/10.1016/j.omega.2006.01.005 - 8. Shafii, M., Hosseini, S.M., Arab, M., Asgharizadeh, E. and Farzianpour, F. (2016) Performance Analysis of Hospital Managers Using Fuzzy AHP and Fuzzy TOPSIS: Iranian Experience. Global Journal of Health Science, 8, 1916-9744.
- 9. Karsak, E.E. (2002) Distance-Based Fuzzy MCDM Approach for Evaluating Flexible Manufacturing System Alternatives. International Journal of Production Research, 40, 3167-3181.
http://dx.doi.org/10.1080/00207540210146062 - 10. Kuo, M.S., Tzeng, G.H. and Huang, W.C. (2007) Group Decision Making Based on Concepts of Ideal and Anti-Ideal Points in Fuzzy Environment. Mathematical and Computer Modeling, 45, 324-339.
http://dx.doi.org/10.1016/j.mcm.2006.05.006 - 11. Torfi, F., Farahani, R.Z. and Rezapour, S. (2010) Fuzzy AHP to Determine the Relative Weights of Evaluation Criteria and Fuzzy TOPSIS to Rank the Alternatives. Applied Soft Computing, 10, 520-528.
http://dx.doi.org/10.1016/j.asoc.2009.08.021 - 12. Tsai, H.Y., Chang, C.W. and Lin, H.L. (2010) Fuzzy Hierarchy Sensitive with Delphi Method to Evaluate Hospital Organization Performance. Expert Systems with Applications, 37, 5533-5541.
http://dx.doi.org/10.1016/j.eswa.2010.02.099 - 13. Van Laarhoven, P.J.M. and Pedrcyz, W. (1983) A Fuzzy Extension of Saaty’s Priority Theory. Fuzzy Sets and Systems, 11, 199-227.
http://dx.doi.org/10.1016/S0165-0114(83)80082-7 - 14. Yang, T. and Hung, C.C. (2007) Multiple-Attribute Decision Making Methods for Plant Layout Design Problem. Robotics and Computer-Integrated Manufacturing, 23, 126-137.
http://dx.doi.org/10.1016/j.rcim.2005.12.002 - 15. Zadeh, L.A. (1965) Fuzzy Sets. Information and Control, 8, 338-353.
http://dx.doi.org/10.1016/S0019-9958(65)90241-X - 16. Ayag, Z. and Ozdemir, R.G. (2006) A fuzzy AHP Approach to Evaluating Machine Tool Alternatives. Journal of Intelligent Manufacturing, 17, 179-190.
http://dx.doi.org/10.1007/s10845-005-6635-1 - 17. Basligil, H. (2005) The Fuzzy Analytic Hierarchy Process for Software Selection Problems. Journal of Engineering and Natural Sciences, 2, 24-33.
- 18. Bojadziev, G. and Bojadziev, M. (1998) Fuzzy Sets Fuzzy Logic Applications. World Scientific Publishing, Singapore.
- 19. Bozdag, C.E., Kahraman, C. and Ruan, D. (2003) Fuzzy Group Decision Making for Selection among Computer Integrated Manufacturing Systems. Computer in Industry, 51, 13-29.
http://dx.doi.org/10.1016/S0166-3615(03)00029-0 - 20. Chang, Y.H., Cheng, C.H. and Wang, T.C. (2003) Performance Evaluation of International Airports in the Region of East Asia. Proceedings of Eastern Asia Society for Transportation Studies, 4, 213-230.
- 21. Chan, F.T.S. and Kumar, N. (2007) Global Supplier Development Considering Risk Factors Using Fuzzy Extended AHP-Based Approach. Omega International Journal of Management Science, 35, 417-431.
http://dx.doi.org/10.1016/j.omega.2005.08.004 - 22. Chen, C.T., Lin, C.T. and Huang, S.F. (2006) A Fuzzy Approach for Supplier Evaluation and Selection in Supply Chain Management. International Journal of Production Economics, 102, 289-301.
http://dx.doi.org/10.1016/j.ijpe.2005.03.009 - 23. Chou, T.Y. and Liang, G.S. (2001) Application of a Fuzzy Multi-Criteria Decision Making Model for Shipping Company Performance Evaluation. Maritime Policy and Management, 28, 375-392.
http://dx.doi.org/10.1080/03088830110049951 - 24. Ertugrul, I. and Tus, A. (2007) Interactive Fuzzy Linear Programming and an Application Sample at a Textile Firm. Fuzzy Optimization and Decision Making, 6, 29-49.
http://dx.doi.org/10.1007/s10700-006-0023-y - 25. Ertugrul, I. and Karakasoglu, N. (2009) Performance Evaluation of Turkish Cement Firms with Fuzzy Analytic Hierarchy Process and TOPSIS Methods. Expert Systems with Applications, 36, 702-715.
http://dx.doi.org/10.1016/j.eswa.2007.10.014 - 26. Hakimi, P.N. and Hozhabr K.K. (2008) Efficiency Comparative Analysis of Big Industries Sector in Iran Provinces: By Using Stochastic Frontier Function. Journal of Knowledge and Development, 16, 115-140.
- 27. Zare Naghadehi, M., Mikaeil, R. and Ataei, M. (2009) The Application of Fuzzy Analytic Hierarchy Process (FAHP) Approach to Selection of Optimum Underground Mining Method for Jajarm Bauxite Mine, Iran. Expert Systems with Applications, 36, 8218-8226. www.elsevier.com/locate/eswa
http://dx.doi.org/10.1016/j.eswa.2008.10.006 - 28. Al-Eraqi, A.S., Mustafa, A. and Tajudin, K.A. (2010) An Extended DEA Windows Analysis: Middle East and East African Seaports. Journal of Economic Studies, 37, 115-139.
- 29. Wu, D., Liang, L., Huang, Z. and Li, S.X. (2005) Aggregated Ratio Analysis in DEA. International Journal of Information Technology & Decision Making, 4, 369-384.
http://dx.doi.org/10.1142/S0219622005001593 - 30. Xu, Z. (2008) On Multi-Period Multiattribute Decision Making. Knowledge-Based Systems, 21, 164-171.
http://dx.doi.org/10.1016/j.knosys.2007.05.007
NOTES

*Corresponding author.




