Journal of Biomedical Science and Engineering
Vol. 5 No. 10 (2012) , Article ID: 23797 , 6 pages DOI:10.4236/jbise.2012.510075
Two types of systems and three types of paradigms in systems philosophy and system science
![]()
Surgut State University, Surgut, Russia
Email: Valery.Eskov@Gmail.com, *firing.squad@mail.ru, Filatovamail@mail.ru, filatov_mik@yandex.ru
Received 3 April 2012; revised 14 August 2012; accepted 29 August 2012
Keywords: Vector of States; Quasiattractor; Chaos; Glimmer
ABSTRACT
Now it is evident that nature and society have a great number of special systems which very differ from traditional objects (systems) of physics, chemists and engineering. For such special (synergetic-chaotic) systems we propose the special third paradigm and construct five basic properties of (unique) systems and on 13 differences in the methods, basic concepts about such systems. The introduction of such basic properties and differences are presented in the article. We postulate the humanity evolution, dynamic of social and political systems, biosphere of Earth, the human organism and his functional systems and many other systems (Universe at all) have all five such properties and must be described according to special synergetic paradigm. Now the authors presents all these special properties and the special table where the differences between deterministic-stochastic systems (and its theoretical approaches) and the synergetic systems (complexity, self-organization systems) were presented more conveniently.
1. INTRODUCTION
More than a century of systems theory development (end of the 19th century—A. Bogdanov, beginning of the 20th century—L. von Bertalanffy, middle and end of the 20th century—N. Wiener и W. R. Ashbу’s cybernetics) has made the humanity to realize that there are three global paradigms in the world. Let us recall that the last (and more global) definition of paradigm was presented by Thomas Kuhn (in his famous book “The structure of scientific revolutions”): “universally recognized scientific achievements that, for a time, provide model problems and solutions for a community of researches”. As a result of paradigm understanding we can research, model and does some future prognosis; what type of theory we can construct according to the paradigm and how we can interpret the prognosis if it realize or not realize. So the global paradigm must be interpreted not only nature but systems dynamics. There are some other definition of paradigm (see the Oxford English Dictionary “a pattern or model, an exemplar” for example) but the global understanding of such word (paradigm needs more wideness interpretation and are only three global paradigms: deterministic-stochastic paradigms (DSP) as two types of bounded paradigms and our, third (chaotic-self-organization) paradigm (TP)). The last we use for unique, third type of systems with chaotic initial, intermediate and final states of its state vector 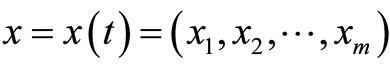 .
.
In W. Weaver’s (1948) representation [1] it may be understood as the abstract classes of systems: “organized simplicity”, “disorganized complexity”, “organized complexity”. If we abstract from the attempt of giving more precise definition to these three types of systems, suggested by W. Weaver, the classification of the authors will be presented in details and definitely [2]. According to three types of global paradigms: stochastic paradigm, (for description of “disorganized complexity” [1]; deterministic paradigm (for understanding and describing “organized simplicity” [1]; and the third (chaotic-selforganization) paradigm describing “organized complexity”, [1])).
Details of the authors’ interpretation and the classification of three types of systems (the background of new classification) are expounded in the first volume of the edition “The Third Paradigm” (the edition will contain 6 volumes and soon will be published, the author is V. M. Eskov). But the authors are to give a brief representation of some basic principles for a clear and formulized view of several fundamental ideas. Otherwise, the novelty and significance of the investigation will be obscure. The authors are going to give new ideas for the world, humanity and other philosophical aspects of systems theory for different specialists from all spheres, including cultural areas.
Briefly, the world science in the field of systems theory is in a systems crisis (we are sorry for tautology), connected with the unwillingness to apprehend the presence of the third type of systems, difficult understanding by different scientific schools, that stirs up irreconcilable discussions. In the USA this type of systems is defined as the complexity and nonlinear dynamics [3], in Europe (H. Haken)—as synergetic systems, in other cases they are defined as complex, self-organizing systems [1,2,4-7]. But all of these are only little part of all, global definitions of complexity—the system of third type according to our classification.
However, the complexity, self-organization, nonlinear dynamics of its behavior does not actually cover their basic, fundamental, key properties, which could be formalized (the concept of complexity, self-organization are not formalized, and simple system may also have nonlinear dynamics, not connecting with the special third type systems). Generally, everything is critical and uncertain, and hence there is basis for a heated discussion, rejection and resentment. Against this background, the main confusion was initiated discussion between H. Haken, and I.R. Prigogine, that has not finished (to the displeasure of both sides). One of the authors of the message (V. M. Eskov) revealed in his book the reasons of this controversy and suggested that the real withdrawal from the system crisis [2].
1.1. Why Are There Two Types of Systems but Three Types of Paradigms?
In his final address to the future generations I. R. Prigogine said “The Die Is Not Cast” [8] about the existence in nature (in society as well) unique (individual and unique) systems (objects, phenomena), that are quite impossible to investigate in the framework of determinism (and we shall add, stochastically too). Prigogine acknowledges that modern science, studying the complexity of the world, deny determinism: they insist that nature is creative at all levels of its organization. The future is not given to us in advance. The authors of the article defined 30 years ago clearly that the “complexity” in the objects of nature with a unique, complex, synergistic (self-organizing) properties of systems cannot be studied within the framework of determinism or stochastics.
In this regard, it should be emphasized that the tragedy of I. R. Prigogine was connected with feeling of (or even understanding) the existence in nature and society of the third, special type of systems. Unique, rare systems being in a continuous “glimmer” and constant teleological evolution, where the huge difference (not like the fluctuations stated by I. R. Prigogine and L. D. Landau) in a continuous “glimmer” that determine the evolution and final state. Understanding of all the contradictions I. Prigogine had always to serve this deterministic-stochastic approach (or paradigm, as defined by the authors of the report)—DSA (or DSP).
To describe the complex and unique systems of the third type DSP is not suitable. Here we need the third paradigm (TP), which is based on 5 basic properties of (unique) systems and on 13 differences in the methods, basic concepts about the state of these unique systems in relation to other deterministic and stochastic systems (we combine them in DSP-type systems). First, the united type of systems is based on two different paradigms (deterministic and stochastic), and, despite their great differences, the similarities between them are essential and fundamental. It is based on the fact that the initial state of any deterministic or stochastic system should be reproducible any number of times, without any restrictions. It is the main feature of the scientific content (in the DSP) in the study of the first type of systems (but subordinated, supposedly, to two different paradigms). Let us consider in more detail the history of differences and communalities in the definition of these two types of systems that the authors combine into DSA-systems. At the same time (before the beginning of this presentation), we note that I. Prigogine stood in the mode of DSA, despite the existence of an understanding and existence of the third paradigm, and the second (non-DSP)-type systems.
The early scientific history demonstrates different types of mind when describing nature. We know a famous Greek proposition about continuously changing the objects properties (in nature proposition about river states: “panta rhei”). Now we understand that the Greek scientists had primitive knowledge about our modern theory of chaotic systems and about objects with chaotic dynamics.
On the other hand, a famous and outstanding Chinese philosopher Confucius (with Dao presentation) and his followers told that there were three types of each man’s social and psychological stage. The first stage of human mind is that everybody has deterministic (according to social laws) state (like for a little child we do input interrupted control to restrict his non-mind freedom). The second one, everyone lives in the stochastic world (everyone can choose the trajectory of his life among some different possibilities). The third one, Dao’s principle makes the choice of the synergetic trajectory of his life possibilities (it is a great possibility of his own choice). Three Dao’s states illustrate the fractal property of different “human-comparable” dynamic systems: the transformation from the deterministic to stochastic stage and after that to the synergetic stage.
As to Dao’s transformation we have similar evolution for human society from traditional (the authors named it deterministic) to technological (named stochastic) society. And a final stage of social evolution is synergetic (knowledge, postindustrial) society—SKPS. Such transformation (deterministic, stochastic and synergetic (chaotic) types of systems) we can observe in science evolution too. I. Newton’s and P. Laplace’s determinism (XVII-XIX centuries) was transformed into stochastic approaching (the beginning of the twentieth century in physics). And now we observe the transformation of stochastic paradigm to final synergetic (chaotic) paradigm (the last third type of paradigm).
So these fundamental laws of science evolution lay down the foundation of the synergetic paradigm and its description of special synergetic complexity (with chaotic-self-organization properties) but deterministic-stochastic paradigms (DSP) may be used for physical, chemical and technical systems because we can repeat and reproduce all states of such DSP-systems (correctly or with some fixed distribution). But for such synergetic systems now it isn’t possible to do strong identification of real distinctions between approaching according to DSP and according to the methods of synergetic paradigm. In science the strong understanding of such distinctions is lacking. We shall demonstrate a special table of differences of the initial state of system’s state vector (SSV)  in phase space of states (PSS)-
in phase space of states (PSS)-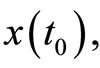 intermediate states of
intermediate states of  ) and the final state of SSV in PSS
) and the final state of SSV in PSS  from three types of paradigms (deterministic, stochastic and synergetic (chaotic)).
from three types of paradigms (deterministic, stochastic and synergetic (chaotic)).
There is a great affinity between deterministic and stochastic paradigms because we can define correctly (and reproducibly) the initial state of SSV  and the final state of DSP systems can be defined precisely or with some distributions (see Table 1).
and the final state of DSP systems can be defined precisely or with some distributions (see Table 1).
There are global laws of fractal evolution of different dynamic systems (for example: unique man, humanity, mankind mind). On the other hand, we have such transformation for science when we observe the change of deterministic paradigm to stochastic paradigm and at the end of such transformation we will create a synergetic paradigm. Let us consider the basic principles as laws for such transformation.
The change of three paradigms according to global dynamic system laws of evolution (deterministic-stochastic-synergetic transformation) has some regularity for scientific evolution. It is based on the notions “certainty” and “uncertainty” [1,8,9]. These notions are connected with three basic stages of any dynamical systems (as complexity). The initial stage is being modeled by system’s state vector (SSV) x in phase space state and  must be defined very correctly. So we must easily repeat each initial state (
must be defined very correctly. So we must easily repeat each initial state (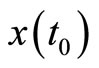 for t = 0 must be definite). Such processes must be certainly repeated for deterministic systems. The same condition we have for deterministic systems for intermediate and final stages of their dynamics. It is possible in physics, chemistry and techniques but it isn’t possible for biological, medical, social, political dynamic systems (BDS, MDS, SDS, PDS) with chaotic behavior of their dynamics. For deterministic processes we must know the initial stage, some mathematical models for systems descriptions and all intermediate, final stages must be defined exactly and correctly. Such processes are given in Table 1 where every stage (the case of full definiteness) is presented as a “+”, when the stage isn’t correctly defined we have “±” and if we don’t know anything about system's dynamics we have “−” (the case of full indefiniteness).
for t = 0 must be definite). Such processes must be certainly repeated for deterministic systems. The same condition we have for deterministic systems for intermediate and final stages of their dynamics. It is possible in physics, chemistry and techniques but it isn’t possible for biological, medical, social, political dynamic systems (BDS, MDS, SDS, PDS) with chaotic behavior of their dynamics. For deterministic processes we must know the initial stage, some mathematical models for systems descriptions and all intermediate, final stages must be defined exactly and correctly. Such processes are given in Table 1 where every stage (the case of full definiteness) is presented as a “+”, when the stage isn’t correctly defined we have “±” and if we don’t know anything about system's dynamics we have “−” (the case of full indefiniteness).
For initial state the second row (presents the probability systems) of Table 1 presents the definite initial stage of SSV in PSS and it must always have “+” (the stage must be repeated unlimitedly). But for intermediate stages 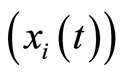 and for the final stage of such processes we have unknown value of SSV in PSS (at final we know only its distribution). Table 1 presents “±” for intermediate stages and “−” for the final stage of such systems with stochastic behavior (see the second row).
and for the final stage of such processes we have unknown value of SSV in PSS (at final we know only its distribution). Table 1 presents “±” for intermediate stages and “−” for the final stage of such systems with stochastic behavior (see the second row).
The third row of Table 1 presents all stages of synergetic systems’ dynamics according to I. Prigogine’s version of complexity behavior (synergetic systems with nonlinear dynamics). For such version the initial stage must be defined precisely and for other stages we have complete uncertainty (“−” and “−” for second and third columns). The uncertainty has great differences in comparison with probable indefiniteness (see the 2nd row and 3rd column) because chaotic processes are not repeatable in principle. But H. Haken’s proposition (about synergetics) has deeper roots (as I. Prigogine’s version) and for these real cases the authors introduces the fourth row where the initial state isn’t defined. Now the authors

Table 1. The role of definiteness (certainty—“+”) and indefiniteness (“–”) in four types descriptions of biological dynamic systems.
postulates: the initial state of every BDS (medical, social, political and other “human-measurable” systems) featured to be uncertain because SSV in PSS performs continuous movement (chaotic movement in specific phase space volume that the authors named as quasi-attractor VG). The chaotic movement in quasi-attractor of SSV till this day was ignored by all researches. We all think that x0(t) = const for t = 0 and dx/dt = 0 but in real nature every SSV in PSS for such complexity (synergetic systems) performs the continuous movement in some VG and parameters of VG—present the real state of BDS (and other synergetic system’s states, not only initial ones).
The authors with many other colleges try to construct modern compartmental-cluster theory of bio-systems (CCTB) where all these special properties of compartmental-cluster structure of biological dynamic systems (BDS) are taken into account [2,10-12].
1.2. Five Properties and Thirteen Differences between the Third Paradigm and DSP
Now we have a special theory (CCTB) where the basic postulate of H. Haken’s proposition was presented [2,10, 12] and the compartmental-cluster theory of bio-systems with modeling of compartmental and cluster structure of different similar systems was described [10-12]. Indeed the CCTB are based on H. Haken’s postulate [4,5] where behavior of separate elements is not investigated and systems have the compartmental-cluster structure (the first basic property of synergetic systems presented by the authors, see Table 2 below) [2,10].
The second property of BDS (and other similar synergetic systems) is connected with “glimmer” property. It means that there are not stationary regimes for BDS or from other way for state vector x(t) we have not dx/dt = 0 and x(0) = const for every time of BDS existence. The authors postulates that every complexity (synergetic BDS) can be described by the system state vector (SSV) in PSS has uninterrupted movement SSV in phase space of state. So all these synergetic systems (BDS, political, social, physical states of separate man or all society) are considered to be “glimmering systems” [2,7].
The third basic property of BDS (and other synergetic systems) is connected with special theological properties. For example, we think mankind has some final purposes (the laws of our self-organization have some theological trajectory). It may be the end of our civilization and the beginning of a new evolution of biosphere. But it doesn’t mean that we don’t have any choice for changing such trajectory of mankind theological future. The authors dreams that synergetic society will do the parallel civilization in Space (not only one) and we shall continue our life in other world (on other planets) if the Earth achieves a catastrophe. So the theological property is the third basic property of BDS and other synergetic systems [2,7].
The forth property of BDS is connected with “glimmering” property but it is not the same because we named it “evolution” [1,2,4-7]. The glimmering processes may be realized in a special volume of phase space named by the authors as a “quasi-attractor”. The volume characterizes the status of BDS (and other synergetic systems) and it is connected with micro-chaotic movements of SSV in phase space. The micro-chaotic movements of all parameters of SSV characterize the glimmering processes of BDS (and other synergetic systems) and nowadays it is a special second property of BDS. The evolution and glimmering property differ from each other because evolution is a macro-property of SSV moving in PSS (for long time) and glimmer is a microproperty of synergetic systems. But all of these properties are the main properties of such systems. So we have many different systems in nature (mankind, separate man, biosphere, Universe ∙∙∙) which we must describe according to synergetic paradigm and its apparatus (including theological property, microand macro-chaotic regimes with evolution and glimmer, compartmental-cluster structure). Such synergetic objects and systems differ from physical, chemical, technical systems and objects and all of these special properties we can demonstrate in special Table 2.
The one that weighs most heavily on proponents of the deterministic/stochastic approach and the most “extravagant” property of BDS, is the property of exceeding the three-sigma limits (for a Gaussian distribution, the probability of falling outside these limits is P < 0.003). In principle, for biological dynamical systems, all evolution of the living occurs beyond the three-sigma limit, i.e., there are huge “biofluctuations”, deviations from the average values. It is specifically such systems, in particular people (geniuses) who create new (also going far beyond the limits of established boundaries) theories and approaches, and new directions in science. All biological processes going beyond the three-sigma boundary should be detected, studied, and measured, and we need to build models for them within the framework of the new theory of chaos and synergetics. The most popular presentation of our fifth biosystem property for economical and political system’s was illustrated in famous monograph of N. Table [9].
In fact, Table 2 includes all five special properties of synergetic systems—complexity (compartmental-cluster structure, “glimmering property” and absence of stable state, theological and evolutionary properties and some properties connected with uniform distribution of all parameters of system’s state vector in phase space and with its existence in special quasi-attractor—the volume of


Table 2. The differences between the approaches of deterministic-stochastic paradigm (DSP) and synergetic paradigm (SP).
phase space where the state vector performs its continuous movement). All these five properties and some other differences illustrate the difference between DSP and SP (their approaching) indeed. We can investigate or neglect such idea as we did before in science. But reality exists out of our mind.
2. CONCLUSIONS
It is evident now that mankind constructs three types of global approaching for scientific describing of different natural and social processes: deterministic, stochastic and synergetic (chaotic) approaching (the last is our construction because our micro-chaos is very different from traditional interpretation of chaos). These three directions of science have some common roots but there are many different details in their construction and development. We must say that three paradigms laying the foundation of the three types of sciences ant it are useful not only in science itself but DSP and SP can describe the evolution of mankind, separate man, the evolution of culture, religion and science at all.
The third paradigm and its applications are not finished and its developments continued now. Not only classic synergetics (but it is different direction as theory of complexity, nonlinear dynamic theory and the theory of self-organizations and chaos) may be useful for description of very special systems which are very differ from physical, chemical or technical systems. For such special synergetic systems we have five very special properties: the contract property of compartmental-cluster structure; evolution property and micro-chaotic movements of its state vector in phase space (with uniform distribution of its parameters in special volume of the phase space named by the authors as quasi-attractor) signed as glimmer; theological property and the possibility overrunning three-sigma’s interval (the property neglected famous statistical property).
The last fifth property indicates that overrunning three sigma’s interval must be investigated actively in case of synergetic systems and the distribution of state vector parameters may be uniform for such systems. The latter proposition turned out to be just a hypothesis but we can’t study and prove this proposition in principle because all synergetic systems have evolution and theological properties. We can't check the systems with continuous and permanent evolution. The similar situation we have in probability theory for J. Bernoulli’s theorem (when frequency P*(A) approaches its probability P(A) with some probability for repeating of the experiments unrestrictedly large (n→∞)). But for synergetic system it is not possible situation because there is not stable state (dx/dt ≠ 0 at all) and such system have uninterrupted evolution.
So the humanity evolution, dynamic of social and political systems, biosphere of Earth, the human organism and his functional systems and many other systems (Universe at all) have all five such properties and must be described according to special synergetic paradigm. Now the authors presents all these special properties and the special table where the differences between deterministic-stochastic systems (and its theoretical approaches) and the synergetic systems (complexity, self-organization systems, ∙∙∙) were presented more conveniently. As a result all of it we must talk about three types of science: deterministic science (as ideal presentation), the stochastic science (more as a real presentation) and the synergetic (complexity, etc.) science (for description of special objects with five properties and special micro-chaotic regimes).
According to the classification (see Table 2) we should investigate the microand macro-chaotic regimes of such synergetic systems and as a result we should calculate the parameters of quasi-attractors. It has been proved and presented that there are differences between I. Prigogine’s and H. Haken’s approaches like now the existing of differences between deterministic-stochastic theory and synergetic theory. The last is evident according to Tables 1 and 2.
REFERENCES
- Weaver, W. (1948) Science and complexity. Rokfeller Foundation, New York.
- Eskov, V.M. (2011) Third paradigm. Samara: Ofort, Samara, 240 p.
- Ebeling, W., Erdmann, U., Dunkel, J. and Jenssen, M. (2000) Nonlinear dynamics and fluctuations of dissipative toda chains. Journal of Statistical Physics, 101, 443-457. doi:10.1023/A:1026407415248
- Haken, H. (1995) Principles of brain functioning: A synergetic approach to brain activity, behavior and cognition (Springer series in synergetics). Springer, New York.
- Mainzer, K. (2007) Thinking in complexity: The computational dynamics of matter, mind and mankind. Springer, New York.
- Bertalanffy, L.V. (1950) An outline of general system theory. British Journal for Philosophy of Science, 2, 134-165. doi:10.1093/bjps/I.2.134
- Wallerstein, I. (1999) The end of the world as we know it: Social science for the twenty-first century. University of Minnesota Press, Minneapolis.
- Prigogine, I.R. (2000) The die is not cast. World Futures Bulletin of the World Futures Studies Federation, 25, 17-19.
- Taleb, N. (2007) The black swan: The imact of the highly impropable. Random House, New York.
- Eskov, V.M. (1996) Models of hierarchical respiratory neuron networks. Neurocomputing, 11, 203-226. doi:10.1016/0925-2312(95)00048-8
- Eskov, V.M., Eskov, V.V. and Filatova, O.E. (2011) Characteristic features of measurements and modeling for biosystems in phase spaces of states. Measurement Techniques, 53, 1404-1410. doi:10.1007/s11018-011-9673-4
- Eskov, V.M., Eskov, V.V., Braginskii, M.Y. and Pashnin, A.S. (2011) Determination of the degree of synergism of the human cardiorespiratory system under conditions of physical effort. Measurement Techniques, 54, 832-837. doi:10.1007/s11018-011-9812-y
NOTES
*Corresponding author.

