Journal of Biomedical Science and Engineering
Vol.5 No.2(2012), Article ID:17641,5 pages DOI:10.4236/jbise.2012.52012
Estimating the number of data clusters via the contrast statistic
![]()
Department of Medical Biophysics, Medical Informatics and Biostatistics, National Medical University, Donetsk, Ukraine
Email: liakh@dsmu.edu.ua, vitaliy.gurianov@dsmu.edu.ua, olgor22@yahoo.com, rogder1964@dsmu.edu.ua
Received 13 September 2011; revised 7 November 2011; accepted 21 November 2011
Keywords: SOM Neural Network; Clustering; Gap Statistic; Silhouette Statistic
ABSTRACT
A new method (the Contrast statistic) for estimating the number of clusters in a set of data is proposed. The technique uses the output of self-organising map clustering algorithm, comparing the change in dependency of “Contrast” value upon clusters number to that expected under a uniform distribution. A simulation study shows that the Contrast statistic can be used successfully either, when variables describing the object in a multi-dimensional space are independent (ideal objects) or dependent (real biological objects).
1. INTRODUCTION
The first stage of data analysis is in its presentation. Cluster analysis can be used for analyzing of multi-dimensional data set [1]. Cluster analysis groups objects based on the information found in the data describing the objects. The goal is that the objects in a group will be similar to one other and different from the objects in other groups. There are many different clustering techniques. One of them is the self-organizing map (SOM) [2] with its related extensions is the most popular artificial neural algorithm for use in unsupervised learning, clustering, classification and data visualization. One of the major challenges in cluster analysis is estimation of the optimal number of “clusters”.
There have been many methods proposed for estimating the number of clusters: gap statistic [3], silhouette statistic [4], jump methods [5], prediction strength [6], methods based on mixture models and inference of Bayesian factors [7,8].
Nowadays this method and its like are widely used for solving various bio-medical problems. Thus, in paper [9] we are offered the method of features phenotype modeling and iterative cluster merging using improved gap statistics. A Gaussian Mixture Model (GMM) is employed to estimate the distribution of each existing phenotype, and then used as reference distribution in gap-statistics. Applying of this algorithm proves very fruitful for imagebased datasets.
In many of bio-medical issues we have to deal with a very large data set [10]. Considerable interest is studies in genes cauterization [11,12]. Thus, study [13] presents method of clustering analysis of large micro array datasets with individual dimension-based clustering (CLIC), which meets the requirements of clustering analysis particularly but not limited to large micro-array data sets. CLIC is based on a novel concept in which genes are clustered in individual dimensions first and in which the ordinal labels of clusters in each dimension are then used for further full dimension-wide clustering. CLIC enables iterative sub-clustering into more homogeneous groups and the identification of common expression patterns. The method in question enables to carry out a very substation analysis of data-sets; however its application is a laborious, full-time job.
While solving biological and especially medico-biological problems we often face the problem of defining not only the optimal number of clusters which characterize this or that pathology, but also of estimating the number of independent factor attributes, i.e. decrease of space dimensionality. One of the reasons that cause it is a high cost of medical attention.
Exposing of strongly correlating attributes will make it possible to lessen the amount of attributes that are necessary for the analysis, and also to cut the number of medico-biological parameters, that characterize this or that pathology. The methods have enumerated don’t solve this problem.
In this paper we suggest a new method called Contrast statistics that enables to estimate effectively the optimal number of clusters, also making possible to estimate the number of independent factorial attributes. Since many methods of estimating the optimal clusters number [9,13] are based on the methods of Gap statistics and Silhouette statistics, which are nowadays considered classical, it’s only natural that these are the methods we used for the comparative analysis with our method. The second section presents the method description. The third contains the results of this method application.
2. METHOD
Let X be a set with N points in a m-dimensional data space. Data is distributed in k clusters (O1, O2,  , Ok are centres of these clusters). We examine a C point, which belongs to the O0 cluster. Then we define the Contrast of C(Cr) by Eq.1
, Ok are centres of these clusters). We examine a C point, which belongs to the O0 cluster. Then we define the Contrast of C(Cr) by Eq.1
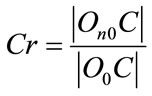 (1)
(1)
where 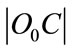 is Euclidean distance C to the centre it’s cluster,
is Euclidean distance C to the centre it’s cluster, 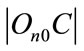 is Euclidean distance C to the nearest cluster besides its own nearest. Points with large
is Euclidean distance C to the nearest cluster besides its own nearest. Points with large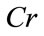 , are well clustered, whereas those with small
, are well clustered, whereas those with small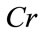 , tend to lie between clusters. Then we characterize quality of the division (k clusters) by Eq.2 (Contrast index)
, tend to lie between clusters. Then we characterize quality of the division (k clusters) by Eq.2 (Contrast index)
 (2)
(2)
Intuitively, when points concentrates in the cluster centres, Contrast (k) will have a high value, when points are distributed uniformly, this value will be low. It will enable us to make a conclusion about the efficiency of the division into the given number of clusters.
3. RESULTS
3.1. Uniform Dataset
We generated datasets (10,000 points uniformly distributed) in m-dimensional space. Then we divided data in k clusters, using SOM technique. Then we calculated Contrast (k) of the division. Figure 1 presents results of the calculation for m = 3, 4, 6, 12 and k = 2, 3,  , 64.
, 64.
The following conclusions can be formulated from this analysis (Figure 1):
1) In the situation of uniformly distributed points (under condition of not great clusters number) dependence Contrast index upon clusters number is described by Eq.3:
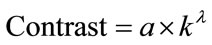 (3)
(3)
where a and l are constants.
2) l (Eq.1) is a positive value and it decreases when dimension of space m increases.
3) When clusters number are great (for the given dimension of space m) the Contrast index doesn’t depend on k (Contrast = Const).
3.2. Computational Implementation
Figure 2 represents an example of Contrast statistic calculation. Five clusters in 4-dimensional space were simulated (total 10,000 points). Contrast indexes for k = 2, 3,  , 36 clusters were calculated.
, 36 clusters were calculated.
The algorithm optimal number of clusters computation can be proposed:
1) Cluster the observed data, varying the total number of clusters from k = 1, 2,  K, calculating Contrast (k).
K, calculating Contrast (k).
2) Obtain the regression line (ln(Contrast) vs ln(k)), which corresponds to uniform distribution, using great k values.
3) Estimate dimension of space number via line slope.
4) Finally choose the optimal number of clusters via Contrast (kopt) greatest deviates from the regression line.
3.3. Contrast Statistic and the Others Techniques
There have been many methods proposed for estimating the optimal number of clusters: Gap statistic [3], Silhouette statistic [4] and so on. In the case of [3] with a large number of model examples the effectiveness of the proposed by author Gap statistics is most convincingly
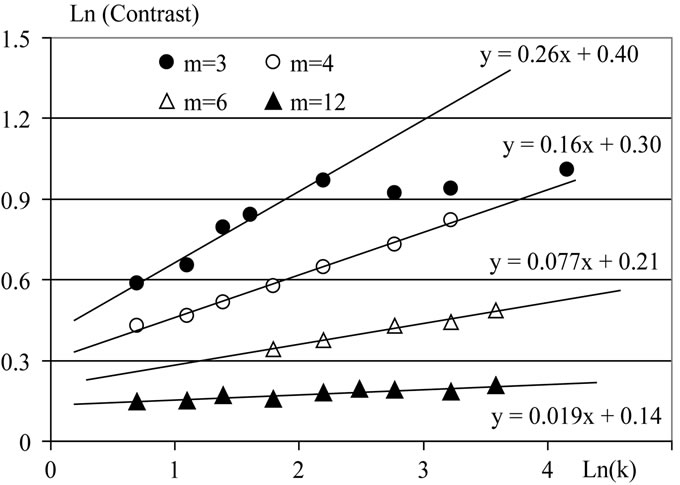
Figure 1. Results for uniformly distributed points in m-dimensional space. The functions y(x) are shown (y = ln(Contrast), x = ln(k)).

Figure 2. Results of Contrast statistic calculation for 5 clusters dataset in 4 dimensional space. Line corresponds to uniformly distributed points in 4-dimensional space.
demonstrated. For application of this approach in the case of k-means the value is calculated by Eq.4,
 (4)
(4)
where —average Euclidean distance from the object to the centre of its cluster in the case of objects distribution under analysis in i-cluster (the quantity of objects in the referent distribution being equal to those the distribution under analysis ). In [3] we presume to compute the
—average Euclidean distance from the object to the centre of its cluster in the case of objects distribution under analysis in i-cluster (the quantity of objects in the referent distribution being equal to those the distribution under analysis ). In [3] we presume to compute the  value for several reference samples on the basis of which we calculate the average value and compute the standard deviation of this value sd (i). As the optimal clusters number such a minimal k is chosen, for which
value for several reference samples on the basis of which we calculate the average value and compute the standard deviation of this value sd (i). As the optimal clusters number such a minimal k is chosen, for which 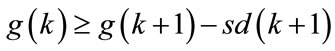 [3].
[3].
While computing Silhouette statistics [4] in the case of cauterization by method of average k, for every j-object of the distribution under analysis the value is calculated by Eq.5.
 (5)
(5)
where a(j) is the average Euclidean distance from the objects to the other objects of the same cluster, b(j) the average Euclidean distance from the object to the objects of the nearest cluster, to which it doesn’t belong. The optimal number of clusters k should be considered as such, for which the average (for all the objects) values s(j) is maximal.
Further on we demonstrate the comparative analysis of application for the optimal cluster number selection the Contrast statistic, the Gap statistic and the Silhouette statistic.
For estimation the Contrast statistic efficiency we analyze some datasets:
1) Datasets simulated in a multi-dimensional space (independent variables), small and large point’s number.
2) Datasets simulated in a multi-dimensional space (dependent variables), small and large point’s number.
3) Practical datasets (real medical and biological data, dependent variables), small and large point’s number.
We applied three different methods for estimating the optimal number of clusters: Gap statistic, Silhouette statistic, Contrast statistic.
The following results can be formulated:
1) For independent variables the Gap statistic is an efficient method of optimal clusters number calculation. The similar results give both Silhouette statistic and Contrast statistic.
2) For dependent variables the Gap statistic isn’t the efficient method. There is a problem on generation of reference distribution (unknown true number of space dimension). Both Silhouette statistic and Contrast statistic can be efficiently used.
3) Total time of Silhouette statistic calculation is as square of cluster size, total time of Contrast statistic calculation is as cluster size.
4) Additionally Contrast statistic allows estimating dimensional number of space for dependent variables (slope the regression line, using great k values) however one of the shortcomings of the estimation is that it is possible only with a small number of independent variables (m < 12).
3.4. Examples
There are measurement data for 150 irises specimen, in equal parts (50 specimen each) belonging to three species (iris setosa, iris versicollor, iris virginica) [14]. For each iris specimen 4 parameters are known. Sepal length, sepal width, petal length, petal width. The task was first set by Fisher and its frequently used in mathematical statistics as a test-trial. While performing the correlation analysis the correlation connection for all the coordinates has been revealed. For finding out the minimal clusters number of this objects set the above proposed method has been applied. The set has been consequently broken up into 1, 2,  , 16 clusters, and for each of these cases Gap statistic, Silhouette statistic, Contrast statistic have been calculated. Figure 3 presents results of the calculation.
, 16 clusters, and for each of these cases Gap statistic, Silhouette statistic, Contrast statistic have been calculated. Figure 3 presents results of the calculation.
Analysis performed for the model task indicates that Gap statistics, Silhouette statistic and Contrast statistics all define the optimal cluster number as equaling to four.
A substantial analysis for each one of the separated clusters clearly demonstrates the biological importance of the solution obtained. In addition to the obtained optimal clusters number, considering the Contrast index dependency on k, we may safely assume, that the number of independent variables, in which the mentioned objects are distributed, is close to 3.
Contrast statistics method was used for analysis of Data of the National Insulin-treated Diabetics Register [15]. Clustering was conducted on a 6324 patients data holding sample. During the SOM mapping, the number of clusters varied from 25 to 3. The clearest data representation structure turned out to be with 3 clusters.
The distinction of the mortality cases from diabetes for differentiated clusters is statistically essential on the significance level p < 0.05 (chi-square test). Difference in disability occurrence in these clusters have the significance level p < 0.05. This allows to conclude, that cluster differentiation in 135-deimensional item space has not just been conducted formally, but content-dependent. In this case, following the analysis results we can say that “less serious cases” were related to the 1st cluster, “most
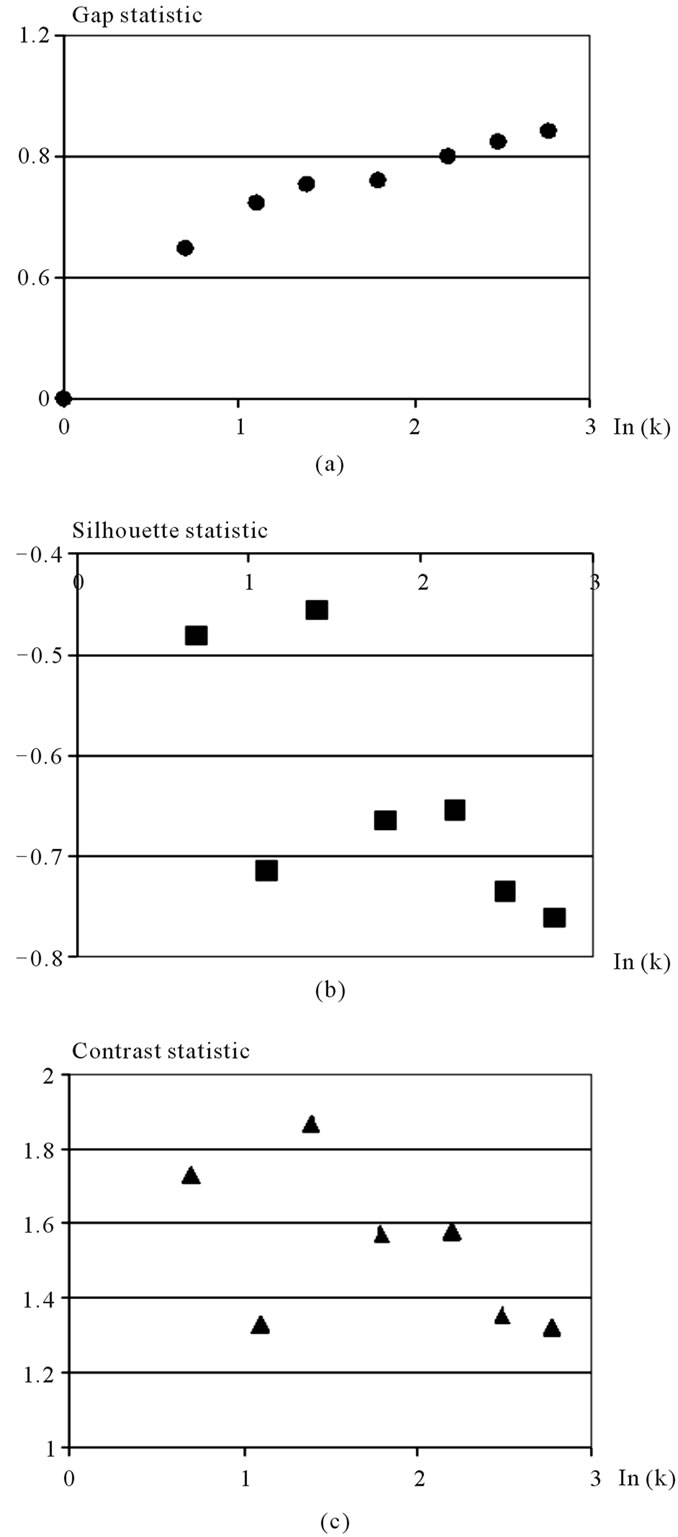
Figure 3. The results of analysis of Ln statistics index dependency of the Ln number of division clusters of the Fisher’s Irises example (4—dimensional space, 3 kinds of flowers) (a) Gap statistic; (b) Silhouette statistic; (c) Contrast statistic.
serious” related to the 3rd cluster. The 2nd cluster contained modest cases [15].
4. CONCLUSION
New Contrast statistic technique the number of data clusters estimation is proposed. The method can be efficiently used for the real large medical and biological dataset. Contrast statistic additionally allows estimating dimensional number of space (only in the case of small space dimentionality) for dependent variables.
![]()
![]()
REFERENCES
- Behbahani, S. and Nasrabadi, A. (2009) Application of SOM neural network in clustering. Journal Biomedical Science and Engineering, 2, 637-643. doi:10.4236/jbise.2009.28093
- Kohonen, T. (1982) Self-organized formation of topologically correct feature maps. Biological Cybernetics, 43, 59-69. doi:10.1007/BF00337288
- Tibshirani, R., Walther, G. and Hastie, T. (2000) Estimating the number of cluster in a dataset via the gap statistic. Technical Report, Department of Biostatistics, Stanford University, Stanford.
- Dudoit, S. and Fridlyand, J. (2002) A prediction—Based resampling method for estimating the number of clusters in a dataset. Genome Biology, 3, 1-21. doi:10.1186/gb-2002-3-7-research0036
- Sugar, C. and James, G. (2003) Finding the number of clusters in a dataset: An information-theoretic approach. Journal of the American Statistical Association, 98, 750- 763. doi:10.1198/016214503000000666
- Tibshirani, R. and Walther, G. (2005) Cluster validation by prediction strength. Journal of Computational & Graphical Statistics, 14, 511-528. doi:10.1198/106186005X59243
- Guo, P., Chen, P. and Lyu, M. (2002) Cluster number selection for a small set of samples using the Bayesian Ying-Yang model. IEEE Transactions on Neural Networks, 13, 757-763. doi:10.1109/TNN.2002.1000144
- Gangnon, R. and Clayton, M. (2007) Cluster detection using Bayes factors from over-parameterized cluster models. Environmental and Ecological Statistics; 14, 69-82. doi:10.1007/s10651-006-0007-7
- Yin, Z., Zhou, X.B., Bakal, C., Li, F.H., Sun, Y.X., Perrimon, N. and Wong, S.T.C. (2008) Using iterative cluster merging with improved gap statistics to perform online phenotype discovery in the context of high-throughput RNAi screensBMC. Bioinformatics, 9, 264.
- Sharma, A., Podolsky, R., Zhao, J. and McIndoe, R.A. (2009) A modified hyperplane clustering algorithm allows for efficient and accurate clustering of extremely large datasets. Bioinformatics, 25, 1152-1157. doi:10.1093/bioinformatics/btp123
- Medvedovic, M. and Sivaganesan, S. (2002) Bayesian infinite mixture model based clustering of gene expression profiles. Bioinformatics, 18, 1194-1206. doi:10.1093/bioinformatics/18.9.1194
- Qin, Z.S. (2006) Clustering microarray gene expression data using weighted Chinese restaurant process. Bioinformatics, 22, 1988-1997. doi:10.1093/bioinformatics/btl284
- Yun, T.Y., Hwang, T.H., Cha, K. and Yi, G.-S. (2010) CLIC: Clustering analysis of large microarray datasets with individual dimension-based clustering. Nucleic Acids Research, 38, W246-W253. doi:10.1093/nar/gkq516
- Kim, J.H., Kohane, I.S. and Ohno-Machado, L. (2002) Visualization and evaluation of clusters for exploratory analysis of gene expression data. Journal of Biomedical Informatics, 35, 25-36. doi:10.1016/S1532-0464(02)00001-1
- Khalangot, N., Gurianov, V., Misko, L. and Harris, N. (2004) Analysis of large diabetic registers: Methodology and some results. Proceedings of the Ninth International Symposium on Health Information Management Research, Sheffield, 15-17 June 2004, 145-150.

