Intelligent Information Management
Vol. 4 No. 4 (2012) , Article ID: 21410 , 10 pages DOI:10.4236/iim.2012.44021
Syntax-Tree Regular Expression Based DFA Formal Construction
Department of Computer Science, King Faisal University, Hofuf, KSA
Email: {nazafar, falsaade}@kfu.edu.sa
Received May 7, 2012; revised June 16, 2012; accepted July 9, 2012
Keywords: Automata Theory; Compiler Verification; Lexical Analyzer; Automated Tools; Z Specification
ABSTRACT
Compiler is a program whose functionality is to translate a computer program written in source language into an equivalent machine code. Compiler construction is an advanced research area because of its size and complexity. The source codes are in higher level languages which are usually complex and, consequently, increase the level of abstraction. Due to such reasons, design and construction of error free compiler is a challenge of the twenty first century. Verification of a source program does not guarantee about correctness of code generated because the bugs in compiler may lead to an incorrect target program. Therefore, verification of compiler is more important than verifying the source programs. Lexical analyzer is a main phase of compiler used for scanning input and grouping into sequence of tokens. In this paper, formal construction of deterministic finite automata (DFA) based on regular expression is presented as a part of lexical analyzer. At first, syntax tree is described based on the augmented regular expression. Then formal description of important operators, checking null-ability and computing first and last positions of internal nodes of the tree is described. In next, the transition diagram is described from the follow positions and converted into deterministic finite automata by defining a relationship among syntax tree, transition diagram and DFA. Formal specification of the procedure is described using Z notation and model analysis is provided using Z/Eves toolset.
1. Introduction
A compiler is itself a computer program which translates computer program written in source language into an equivalent machine code. The translation process is called compilation divided into phases reducing complexity of the compiler. The source code is always written in a higher level language in comparison to machine code. The higher level languages are usually complex in nature and consequently increase the level of abstraction between source code and the resulting machine code. Therefore, the increased complexity requires formalizing such abstract structures for construction and verification of a compiler.
Compiler construction is considered as an advanced research area due to the size and complexity of the code generated. The design and construction of a fully verified compiler will remain a challenge of the twenty first century. Although there exists much work on compiler construction and verification but it needs further investigation. This is because the bugs in the compiler can lead to an incorrect machine code even the source program is completely verified to be correct. Bugs which are detected in the executable machine code might be due either the source program or the compiler itself. It means writing correct compiler is more important than writing a correct program to be compiled which has led the scientific community to investigate in this area.
Formal methods are mathematics-based techniques used for specification and verification of systems [1]. The process of verification means applying formal techniques to verify the properties of systems to be correct. Formal verification targets the program to check its semantics by giving precise meanings to that program. Formal specification is a mathematical description of a system in terms of set theory and first order or higher logic. The benefits of using mathematics in systems development are obvious. Although, there are some disadvantages of using mathematical notations but the application of formal methods has proved that its use is required for correct modeling and specification of systems [2].
Lexical analyzer is an important part of compiler which scans input stream dividing groups into tokens. The tokens are sequences of characters which have meanings in collective format. The preliminary results of this research describing formal construction of syntax tree from regular expression were described in [3]. In that research, some errors and inconsistencies were identified which are fixed and refined here. In this paper, direct formal construction of deterministic finite automata (DFA) based on regular expression is presented using Z notation. Regular expression, which is in fact the source program, is described by defining all of its possible constructs and variables. The regular expression is augmented by joining a special symbol at the end. An abstract syntax tree is described based on the augmented regular expression. The operators of the regular expression are assumed as internal nodes and alphabets are taken as children nodes of the syntax tree. Then formal description of three important operators checking null-ability and computing first and last positions of all the internal nodes of the syntax tree are described. Nullable is a Boolean function having value true or false and its value depends upon the type of node. First and last position functions are collection of identifiers of a node computed based on its children. The nullable and positions functions are used for description of the follow position function used for transition diagram. Finally, the diagram is converted into deterministic finite automata by defining a relationship among syntax tree, transition diagram and DFA. Formal specification of the algorithm is described using Z notation and model analysis is provided using Z/Eves toolset.
Although integration of approaches has become a wellresearched area in computer science [4-6] but there does not exist much research work on construction and verification of compiler by linking formal techniques and automata theory. Dong et al. have described an integration of timed automata and Object Z [7,8]. R. L. Constable has presented formal description of few important concepts of automata theory [9,10]. A formal relationship is explored between Petri-nets and Z notation in [11]. Formal analysis of UML is presented in [12,13] using B. An introduction to algebraic structures is investigated using fuzzy automata in [14]. A formal procedure of fuzzy automata and language theory is discussed in [15]. An important notion of algebraic and automata theories is presented in [16]. Rest of the paper is organized as follows:
In Section 2, an introduction to Z is given. In Section 3, reasoning to construct verified complier is provided. Formal construction of DFA is described in Section 4. Formal analysis of the model is presented in Section 5. Conclusion and future work are discussed in Section 6.
2. An Introduction to Z Notation
Formal methods are mathematical approaches used for describing properties of software systems using computer tools. These techniques are based on discrete structures such as logic, sets, relations, functions, graphs and automata. Formal approaches may be classified as property oriented and model descriptive. Property based methods are used to describe software in terms of properties and invariants. Model oriented methods are used to construct model of a system emphasizing statics and dynamics of a software system. Although there are various formal notations, the integration of formal and existing approaches for complete and consistent description of systems is still required at the current stage of development of formal methods.
There exist various traditional methods which are used for expressing software specifications using computer tools for checking properties of systems. The use of such methods requires a full commitment because the specification of the system must be used to construct a complete and consistent model which will be assumed as a baseline for the further development. For incomplete models such methods are not effective, however, for a complete validation and verification of large scale software specification, it needs to apply mathematics-based techniques to overcome the weaknesses of these traditional approaches. Experience of applying formal notations shows that it is a best option for modeling complex particularly safety critical systems for checking and verifying the properties.
Z notation is a model centered approach based on fundamental structures such as, sets, sequences, bags, relations, functions and, predicate and propositional logic used at an abstract level of specification [17]. The Z is usually used for specifying behavior of sequential programs by the abstract data types and has standard set operators, including union, intersection, comprehensions, Cartesian products and power sets. The Z allows organizing a system into its smaller components using a powerful data structure named schema. The schema defines a way in which state of a system can be specified and further refined by describing detail of a system. Schema has two parts one for variables definitions and other for defining properties of the variables. Refinement is a promising way of Z supporting verifiable transformation from an abstract specification into an executable code. Specification described in Z can further be refined and transformed to an implemented system.
3. Lexical Analyzer
The primary objective of compiler construction is to prove that it is correct and error free. Constructive formulation of showing correct compiler in terms of syntax and semantics translation processes from source to target languages effectively is a major issue in compiler construction. As a sub-problem, compiler verification has become an open research problem in compiler construction. Compiler verification is an area of software engineering in which it is required to prove that compiler behaves exactly as the language description. Software testing and use of formal approaches are two main techniques for validation and verification in construction of a compiler. Testing of compiler has various disadvantages similar to testing of other computer programs. It is impossible to prove by testing that a compiler is completely correct, error free and optimized. There exists much research work showing and referring that most of the tested compilers have bugs and errors [18]. Therefore, it is required to find approaches for correct and optimal construction of compiler. Application of formal methods in compiler verification is an alternative way to find proofs ensuring correctness and reducing complexity of code of construction procedure. It is realized that construction of a fully verified compiler has become a challenge of the twenty first century [19].
The main functionality of a compiler is to translate a source code into an executable and optimized machine code. An accuracy in compiler construction has much importance because the bugs in the compiler can lead to an incorrect code even the source program is verified. Functionality of lexical analyzer is to scan the input stream of characters from left to right and grouping it into tokens. The tokens are sequences of characters having meanings in a grouped format. Verification of lexical analyzer is an important phase of compiler. There are two primary methods for implementing the lexical analyzer. The first one is a hard coded program to perform the scanning tasks in which main loop in the program reads characters one by one from the input program and uses a switch statement to process it. The output of the procedure is a sequence of tokens from the source program. The second one uses regular expressions and automata theory to model the scanning process. In this method, the source program is read character by character beginning with the start state. After reading a character, the transition function is used to move from current state to the next one. In a final state, it is checked if the token read is reserved word, it is passed to the token stream as output, otherwise, its name is put in the symbol table if does not exist already. After a final state is reached, an associated action is performed and the same process is continued. If we are not able to reach a final state an error is encountered. In this case, error handling called upon is used for error recovery. The input is a regular expression and output is a collection of tokens identified by an automaton [20].
4. Formal Specification
In this section, at first, benefits of formal specification are addressed. Then direct formal construction of deterministic finite automata based on regular expression is presented using Z notation. A syntax tree is constructed from regular expression before construction of the automaton.
4.1. Importance of Specification
Formal specification is a description of a system using mathematical notations and abstract models in terms of set theory and first order or higher order logic. The benefits of using mathematics in system development are obvious, for example, the models are precise and un-ambiguous unlike the model described in natural languages which are often used for traditional description and specification of systems. There are some disadvantages of using mathematical notations. For example, people understand more use of natural languages than complex mathematical structures in the area of computer science. However, the uses and benefits of formal methods are observed in modeling and designing of computer systems.
4.2. Definitions
Symbol is an abstract entity. Letters, digits and punctuation are examples of it. Alphabet is a finite set of symbols used to build larger structures. In automata theory, alphabet is usually denoted by the Greek letter sigma ∑.
Example: ∑ = {a, b, c} is an alphabet, where a, b, c are symbols, and abcb is a structure.
Empty String: consists of zero symbol and is denoted by ε.
∑*: is a set of all possible strings that can be generated from a given alphabet ∑.
Regular Expression: is a rule to define the set of words that are valid tokens in a formal language. The regular expressions are usually built up from three operators named as concatenation, alternation and repetition.
4.3. Regular Expressions
Formal specification of extended regular expression is given in this section. Then regular expression is generalized by removing the special symbol as an end character which is used to show the end of input string given to the lexical analyzer. Internal node of the syntax tree is defined to have information including left and right positions, and nullable variables. The syntax tree is described based on the given regular expression. Then functions for computing left positions, right positions and nullable operator for every node of the syntax tree are described. Further, follows of all internal nodes are computed. Finally, deterministic finite automata is described based on the transition diagram constructed from the syntax tree. Although we are well-acquainted with the regular expressions but a brief review is given below before its formal description.
In formal specification of extended regular expression, four main components are assumed as listed in the schema ERE given below. The first one is terminals which is a collection of all the alphabets of the language. The second is a set of operators representing internal nodes in the syntax tree. The operators has values concatenation, alternation (union) and repetition. The third one is a collection of symbols which is a finite set of symbols other than operators and terminals representing children in the syntax tree. The fourth component is extended regular expression represented by ere and is a sequence of symbols. The Symbol, Terminal and Operator are sets at an abstract level of specification over which operators, for example, union, intersection and complement cannot be defined.
[Symbol]; Terminal = = Symbol Operator = = Symbol In first part of the schema ERE, definitions of variables describing extended regular expression are given. Invariants over the variables are defined in the second part of the schema in terms of properties. The invariants prove the well-defined-ness of the variables. In definition of variables, terminals has a type of power set of Terminal. The symbols has a type of power set of Symbol. The variable operators has a type of power set of Operator. The last one regular expression has a sequence type consisting of alphabets, operators and symbols.
In the schema, star, conc and or symbols are used to represent repetition, concatenation and alternation. The symbols, lp, rp and hash are used to represent left parenthesis, right parenthesis and hash symbol. The hash symbol is put at the end of file as mentioned above.

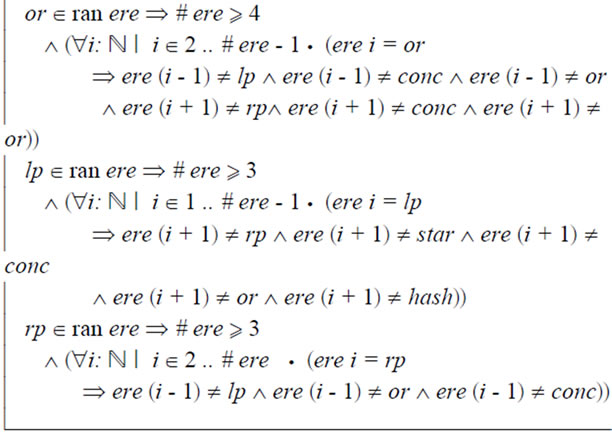
Invariants: 1) The intersection of sets terminals and operators in the grammar is an empty set. 2) Each element in the set of terminals is an element of set of symbols. 3) Each element in the set of operators is also an element of set of symbols. 4) The repetition, concatenation and alternation are elements of the set of operators. 5) The left parenthesis, right parenthesis and hash are elements of the set of symbols. 6) The last element of input string is hash symbol showing end of file. There does not exit hash symbol in rest of the input string. 7) If the regular expression is non-empty, then its left most element cannot be the alternation, repetition or concatenation operator. Further, the first element cannot be right parenthesis. 8) If the regular expression is non-empty, then its right most element cannot be the alternation or concatenation operator. The last element cannot be left parenthesis. 9) If repetition symbol is an element of regular expression then cardinality of the regular expression is more than 2 and on the left of repetition symbol there must be either terminal or right parenthesis. 10) If concatenation operator is an element of the regular expression then cardinality of the regular expression is more than 2. Further, on the left of the concatenation operator there must be either a terminal or it should be the right parenthesis. Furthermore, a terminal or left parenthesis must be on the right hand side of the concatenation operator. 11) If an alternation operator is an element of the regular expression then cardinality of the regular expression is more than 3. The left parenthesis, concatenation operator and alternation operator cannot be on the left hand side of the alternation operator. Further, right parenthesis, concatenation operator and alternation operator cannot be on the right hand side of the alternation operator. 12) If left parenthesis is an element of regular expression then cardinality of the regular expression is more than 2. Further, the right parenthesis, repetition operator, concatenation operator, alternation operator and hash symbol cannot be on the right hand side of the left parenthesis. 13) If right parenthesis is an element of regular expression then cardinality of the regular expression is more than 2. In addition to it, left parenthesis, alternation operator and concatenation operator cannot be on the left hand side of the right parenthesis.
We have described formal definition of extended regular expression. Our objective is to construct deterministic finite automata from extended regular expression based on the construction of syntax tree. The syntax tree is a tree having left and right children which might be itself trees. The left and right children may not contain the hash symbol (end of input symbol). Therefore, the extended regular expression is generalized to describe regular expression using the RE schema given below. The range subtraction operator in Z notation is used to remove the hash symbol from the extended regular expression defined above.

4.4. Syntax Tree Construction
The syntax tree from the augmented regular expression is described below. Before description of the syntax tree a generic definition of an internal node of the tree is given below using the schema Node. The schema consists of eight variables. The first one is sn termed as sequence number (node identifier) which is of type of natural number. The second number is node type. There are four types of nodes that is terminal, internal, null and hash node. The third one is operator type associated with a node. The operator variable has four types namely, alternation, concatenation, repetition and null. The fourth and fifth variables represent the left and right children of the tree. The sixth and seventh variables represent the first and last position of a node of the syntax tree and are of types of power set of natural numbers. The last one is nullable variable having two values either true or false to check nullability of a node.

Invariants: 1) If node is an internal one then sequence number is zero. 2) If the node is null type then nullable variable has true value, the first and last position variables are empty, and left and right children are null tree. 3) If the node is terminal type then nullable variable has false value. Further, the operator type is null. The first and last position variables contain only the sequence number of the node.
The syntax tree is described using the schema SyntexTree given below by defining a relationship between regular expression and syntax tree. The schema consists of five components in addition to the ERE schema. The first one represents the null tree. The second one represents the root identifier. The third one defines all the possible nodes of the syntax tree. The fourth is used to define a relationship between parent and the children in addition to the parent identifier. The last one is a function defining follows of all the sequence nodes. The description of ERE schema components are already given in the definition of extended regular expression.

Invariants: 1) The null tree and range of parent function are disjoint. 2) The union of null tree and the nodes in the parent function belong to the tree. 3) The domain and range of parent function belong to set of all the nodes of the tree. 4) Each element in the set of nodes of the tree is either in the domain or in the range of the parent function.
4.5. Operators Specification
Formal specification of nullable, first and last positions, and follow functions is given in this section. Nullable is a Boolean function having value true or false. First and last position functions are collection of identifiers of the node computed based on the children nodes. All of these functions take syntax tree as input in first part of a schema and verification properties are defined in the second part of the schema.
The nullable variable of the node is checked and verified based on values of the nullable variables of the children using the Nullables schema. Three types of nodes namely, alternation, concatenation and repetition are assumed. The first two functions, that is, nullable and positions will be used for the description of follow position function. After computing follow positions of the internal nodes of the abstract syntax tree deterministic finite automata will be constructed in the next sub-section.

Invariants: 1) If the node of the syntax tree is alternation type then it is nullable if and only if one of its children is nullable. 2) If the node of the syntax tree is concatenation type then it is nullable if and only if both of its children are nullable. 3) If the node of the syntax tree is repetition type then it is nullable if and only if its child is nullable.
The first position function of a node n is a set of positions in the sub-tree rooted at n that correspond to the first symbol of at least one string in the language described by a part of the regular expression rooted at n. The last position function of the node n is the set of positions in the sub-tree of the syntax tree rooted at n that correspond to the last symbol of at least one string in the language described by the sub-expression of the regular expression rooted at n. The first and last position functions are described by the schema LRPositions.

Invariants: 1) If a node of the syntax tree is an alternation type then its first position is union of first positions of its left and right children. 2) If the node is an alternation type then its last position is union of the last positions of its left and right children. 3) If the node is concatenation and its left child is nullable then first position of the node is union of first positions of its left and right children. If left child is not nullable then first position of the node is same as first position of its left child. 4) If the node is concatenation and its right child is nullable then last position of the node is union of last positions of its left and right children. If right child is not nullable then right position of the node is same as last position of its right child. 5) If the node is repetition type then first and last positions of the node are same as first and last positions of its child respectively.
Formal specification of the follows position function is described based on the nullable and, first and last position functions. The procedure of computing follows position is described and its explanation is given as invariants. After computing follows, the transition diagram can be created. Based on the transition diagram, the deterministic finite automata is constructed in the next subsection.
È
Invariants: 1) If a node n of the syntax tree is an alternation or concatenation type, n1 and n2 are its children then for each element x in the last position of n1, the new follows of x = follows of x already computed union first position of n2. 2) If a node n of the syntax tree is repetition type then for each element x in the last position of n, the new follows of x is equal to old follows of x union first position of n.
4.6. Construction of DFA
The Kleene theorem [21] states that a deterministic finite automata (DFA) can be converted into a regular expression and vice versa. An efficient and correct conversion is one of the important area of research in the formal theory of languages. For this purpose, several methods have been proposed [22-28]. In this paper, formal construction of deterministic finite automata is described from the regular expression based on the syntax tree directly. The formal mechanism of syntax tree construction is described above by the supporting algorithms. The formal specification of DFA construction is provided in the following.
The formal specification is described by using the schema DFA which consists of five component in addition to SyntexTree schema. The DFA schema defines a relationship between syntax tree and deterministic finite automata. The syntax tree is converted into DFA by extracting the information and storing into the required components, namely, initial state, set of all states, alphabets, transition function and set of final states of the required automata. The definitions of the components are given in first part and relationship between syntax tree and automata is provided in the second part of the schema.
È
Invariants: 1) The initial state is an element of set of all the states of the resultant automata. 2) Each element in the set of final states is an element of set of total states. 3) For every state and for every alphabet there is a transition in the automata. 4) Initial state is root of the syntax tree. 5) Alphabets of the automata are same as terminals of the grammar. 6) The transition function is defined based on the follows positions of every terminal. For every state s1 and for every alphabet a there exists a state s2 where s2 is union of collection of follows of all the element of s1 calculated at node a. Hence, there will be a function from s1 to s2 by reading a. 7) The state is final if it contains hash symbol.
5. Formal Analysis
Formal analysis for the Z specification is provided in this section. Although computer tools improve quality of software systems but there does not exist any real computer tool which may assure complete correctness of a model. That is why even the specification is formally well-written using any of the specification language, it may contain potential bugs and errors. Hence, an art of writing a formal specification does not provide any guarantee that the system underhand is complete, consistent and correct. If the formal specification is analyzed and validated using computer tools, it increases quality and confidence over the system to be developed. On the other hand, we have observed that knowledge and experience of using computer tools is an art which must be practiced before model analysis.
There exists various tools for analyzing the Z specification. The Z/Eves is a one of the powerful tools used here for analyzing the specification for construction of DFA directly from a regular expression. A snapshot of the specification analysis is presented in Figure 1.
In the Figure, the first column on the left hand side shows syntax checking. The second column in the Figure represents further analysis and proof correctness of the specification. The symbol “Y” shows that the formal specification is correct syntactically and proof is also correct. If there is symbol “N” instead of “Y” it shows existence of errors. There are eight schemas described in the formal specification which are fully analyzed. All of the schemas are checked to prove that specification is correct in syntax and has a correct proof obligation. Some schemas of the specification were proved using reduction techniques available in the toolset. Summary of the results is presented in Table 1. In first column of the Table, name of the schema is given. In column 2, the symbol “Y” indicates that all schemas are well-defined and proved. Domain checking, reduction and proof by reduction are represented in columns 3, 4 and 5 respectively. The character “Y” annotated with “*” symbol shows that the schema is proved by performing reduction on the specification in predicates part to make specification more meaningful.
6. Conclusions
Compiler construction is an advanced research area because of size and complexity of the code generated. Correctness, verification, optimization and generalization are some of its main issues. The source code is usually written in higher level languages which is complex in nature and consequently increases abstraction. Hence, design and construction of a fully verified and error free
Figure 1. Snapshot of the formal analysis.
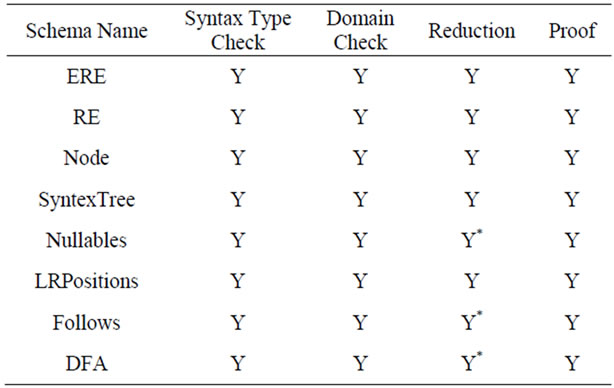
Table 1. Results of formal analysis.
compiler has become a challenge of the current century.
In this paper, formal construction procedure of deterministic finite automata (DFA) from regular expression is presented. Syntax tree is described based on regular expression. Then formal description of required operators is described. The transition diagram is constructed from the follow positions and then converted into DFA. Formal specification is described using Z and analyzed by Z/Eves toolset.
The Z is used in this research because of abstraction and computer tool support. We observed that the use of Z/Eves enhanced reliability and correctness of the models. It is realized that the formal specification helped us to make it possible resolving ambiguities and inconsistencies in the models. Several tools exist to support formal specification written in Z but the Z/Eves is found a powerful one to analyze the specification because of its rich mathematical notations. The Z/Eves made it possible to reason about behavior of the specification more effectively. It is realized that a need for such tools is required in other applications including pattern recognition, pattern matching and defining queries in databases. An exhaustive survey of existing work was performed [29- 37] but our approach is different because of abstract and conceptual level integration. Verification of other concepts related to compiler will appear soon.
REFERENCES
- C. J. Burgess, “The Role of Formal Methods in Software Engineering Education and Industry,” Technical Report, University of Bristol, Bristol, 1995.
- D. Richard , K. R. Chandramouli and R. W. Butler, “Cost Effective Use of Formal Methods in Verification and Validation,” Foundations V&V Workshop, 2002.
- N. A. Zafar, “Automatic Construction of Formal Syntax Tree Based on Regular Expressions,” The 2012 International Conference of Computer Science and Engineering (ICCSE), 2012, in Press.
- H. Beek, A. Fantechi, S. Gnesi and F. Mazzanti, “State/ Event-Based Software Model Checking,” Integrated Formal Methods, Vol. 2999, 2004, pp. 128-147. doi:10.1007/978-3-540-24756-2_8
- O. Hasan and S. Tahar, “Verification of Probabilistic Properties in the HOL Theorem Prover,” Integrated Formal Methods, Vol. 4591, 2007, pp. 333-352. doi:10.1007/978-3-540-73210-5_18
- F. Gervais, M. Frappier and R. Laleau, “Synthesizing B Specifications from EB3 Attribute Definitions,” Integrated Formal Methods, Vol. 3771, 2005, pp. 207-226. doi:10.1007/11589976_13
- J. S. Dong, R. Duke and P. Hao, “Integrating Object-Z with Timed Automata,” 10th IEEE International Conference on Engineering of Complex Computer Systems, Singapore, 16-20 June 2005, pp. 488-497.
- J. S. Dong, et al., “Timed Patterns: TCOZ to Timed Automata,” The 6th ICFEM, Seattle, 8-12 November 2004, pp. 483-498.
- R. L. Constable, et al., “Formalizing Automata II: Decidable Properties,” Technical Report, Cornell University, Ithaca, 1997.
- R. L. Constable, et al., “Constructively Formalizing Automata Theory,” Foundations of Computing Series, MIT Press, Cambridge, 2000.
- M. Heiner and M. Heisel, “Modeling Safety Critical Systems with Z and Petri Nets,” International Conference on Computer Safety, Reliability and Security, Toulouse, 27-29 November 1999, pp. 361-374. doi:10.1007/3-540-48249-0_31
- H. Leading and J. Souquieres, “Integration of UML and B Specification Techniques: Systematic Transformation from OCL Expressions into B,” Asia-Pacific Software Engineering Conference, Vandoeuvre-les-Nancy, 2002, pp. 495-504.
- H. Leading and J. Souquieres, “Integration of UML Views Using B Notation,” Proceedings of Workshop on Integration and Transformation of UML Models, Málaga, 11 June 2002.
- W. Wechler, “The Concept of Fuzziness in Automata and Language Theory,” Akademic-Verlag, Berlin, 1978.
- N. M. John and S. M. Davender, “Fuzzy Automata and Languages: Theory and Applications,” Chapman & Hall, London, 2002.
- M. Ito, “Algebraic Theory of Automata and Languages,” World Scientific Publishing Co., New York, 2004. doi:10.1142/9789812562685
- J. M. Spivey, “The Z Notation: A Reference Manual,” Printice-Hall, Englewood Cliffs, 1989.
- C. Lindig, “Random Testing of C Calling Conventions,” Proceedings of the Sixth International Symposium on Automated Analysis-Driven Debugging, Monterey, 19-21 September 2005, pp. 3-12.
- J. A. Anderson, “Automata Theory with Modern Applications,” Cambridge University Press, Cambridge, 2006. doi:10.1017/CBO9780511607202
- M. van den Brand, A. Sellink and C. Verhoef, “Generation of Components for Software Renovation Factories from Context-Free Grammars,” Proceedings of the Fourth Working Conference on Reverse Engineering, Amsterdam, 6-8 October 1997, pp. 144-153. doi:10.1109/WCRE.1997.624585
- M. Balakrishna, D. Moldovan and E. K. Cave, “Automatic Creation and Tuning of Context-Free Grammars for Interactive Voice Response Systems,” Proceedings of 2005 IEEE International Conference on Natural Language Processing and Knowledge Engineering, Dallas, 30 October-1 November 2005, pp. 158-163.
- L. Pedersen and H. Reza, “A Formal Specification of a Programming Language: Design of Pit,” Second International Symposium on Leveraging Applications of Formal Methods, Verification and Validation, Grand Forks, 15-19 November 2006, pp. 111-118.
- D. P. Tuan, “Computing with Words in Formal Methods,” Technical Report, University of Canberra, Canberra, 2000.
- A. Hall, “Correctness by Construction: Integrating Formality into a Commercial Development Process,” Praxis Critical Systems Limited, Vol. 2391, 2002, pp. 139-157.
- D. K. Kaynar and N. Lynchn, “The Theory of Timed I/O Automata,” Morgan & Claypool Publishers, San Rafael, 2006.
- D. Jackson, I. Schechter and I. Shlyakhter, “Alcoa: The Alloy Constraint Analyzer,” Proceedings of the 22nd International Conference of Software Engineering, Limerick, 4-11 June 2000, pp. 730-733.
- D. Aspinall and L. Beringer, “Optimisation Validation,” Electronic Notes in Theoretical Computer Science, Vol. 176, No. 3, 2007, pp. 37-59. doi:10.1016/j.entcs.2006.06.017
- S. Briaisa and U. Nestmannb, “A Formal Semantics for Protocol Narrations,” Theoretical Computer Science, Vol. 389, 2007, pp. 484-511. doi:10.1016/j.tcs.2007.09.005
- L. Freitas, J. Woodcock and Y. Zhang, “Verifying the CICS File Control API with Z/Eves: An Experiment in the Verified Software Repository,” Science of Computer Programming, Vol. 74, No. 4, 2009, pp. 197-218. doi:10.1016/j.scico.2008.09.012
- S. E. Kleene, “Representations of Events in Nerve Nets and Finite Automata, Automata Studies,” Princeton University Press, Princeton, 1956, pp. 3-42.
- J. Sakarovitch, “Elements de Theorie des Automates,” Cambridge University Press, Vuibert, 2003.
- J. Sakarovitch, “The Language, the Expression, and the Small Automaton, Implementation and Application of Automata,” 10th International Conference (CIAA), Lecture Notes in Computer Science, Vol. 3845, 2005, pp. 15-30.
- V. M. Glushkov, “The Abstract Theory of Automata,” Russian Mathematical Surveys, Vol. 16, No. 5, 1961, pp. 1-53. doi:10.1070/RM1961v016n05ABEH004112
- R. F. McNaughton and H. Yamada, “Regular Expressions and State Graphs for Automata,” IEEE Transactions on Electronic Computers, Vol. 9, No. 1, 1960, pp. 39-57. doi:10.1109/TEC.1960.5221603
- J. A. Brzozowski, “Derivatives of Regular Expressions,” Journal of Association for Computing Machinery, Vol. 11, No. 4, 1964, pp. 481-494. doi:10.1145/321239.321249
- V. Antimirov, “Partial Derivatives of Regular Expressions and Finite Automaton Constructions,” Theoretical Computer Science, Vol. 155, No. 2, 1996, pp. 291-319. doi:10.1016/0304-3975(95)00182-4
- F. Gecseg and M. Steinby, “Tree Languages,” Handbook of Formal Languages, Vol. 3, 1997, pp. 1-68.

