Intelligent Information Management
Vol.2 No.4(2010), Article ID:1721,4 pages DOI:10.4236/iim.2010.23034
On the Reflected Geometric Brownian Motion with Two Barriers
1Department of Mathematics, Tianjin University of Science and Technology, Tianjin, China
2College of Economics&Management, Tianjin University of Science and Technology, Tianjin, China
E-mail: zhanglidong1979@yahoo.com.cn, dusx@tust.edu.cn
Received January 28, 2009; revised March 3, 2010; accepted April 7, 2010
Keywords: Geometric Brownian Motion, stationary distribution, First Passage Time
Abstract
In this paper, we are concerned with Reflected Geometric Brownian Motion (RGBM) with two barriers. And the stationary distribution of RGBM is derived by Markovian infinitesimal generator method. Consequently the first passage time of RGBM is also discussed.
1. Introduction
We consider a finite-capacity fluid queue, the level of which at time 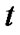 is denoted by
is denoted by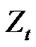 . And
. And 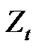 satisfies the following differential equation:
satisfies the following differential equation:
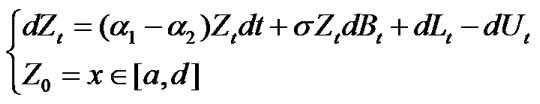 (1)
(1)
This model shows fluid arrives into this queue at rate 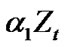 and leaves the queue at rate
and leaves the queue at rate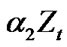 . This fluid level can be also varied by a local variance function
. This fluid level can be also varied by a local variance function  and a standard Brownian motion
and a standard Brownian motion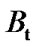 .
. 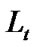 and
and 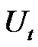 are nondecreasing processes, interfering only when
are nondecreasing processes, interfering only when  hits a or d and make
hits a or d and make  vary between a and d.
vary between a and d.
In particular, when  and
and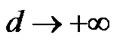 ,
,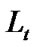 and
and 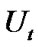 disappear. Then the process
disappear. Then the process 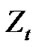 becomes Geometric Brownian Motion. So we call
becomes Geometric Brownian Motion. So we call  determined by (1) Reflected Geometric Brownian Motion(RGBM).
determined by (1) Reflected Geometric Brownian Motion(RGBM).
Speak precisely, we are concerned with RGBM 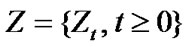 with two barriers a and d (d > a > 0), which is defined by
with two barriers a and d (d > a > 0), which is defined by
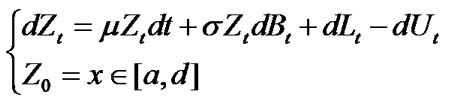 (2)
(2)
where 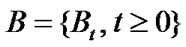 is a standard Brownian Motion,
is a standard Brownian Motion,  and
and 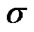 are constants and satisfy
are constants and satisfy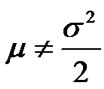 .
.
Moreover, the processes L and U are uniquely determined by the following property [1,2]:
1) Both L and U are continuous nondecreasing processes with ;
;
2) L and U increase only when  and
and ; respectively, i.e.,
; respectively, i.e.,
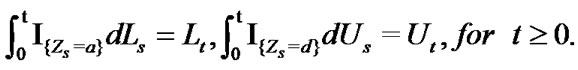
According to the theory of stochastic differential equation, (2) is equivalent to
 (3)
(3)
Such a process is a regenerative Markov process with state space [a,d] compact. Then it has a unique stationary distribution [1,3,4]. In the coming section, our objective is to derive the stationary distribution and give an expression for the Laplace Transform of the first passage time of RGBM  by the method in [5-7].
by the method in [5-7].
2. Main Results on RGBM
2.1. On the Stationary Distribution of RGBM
In this section, we firstly give a Lemma on the stationary distribution of the reflected process  with two-sided barriers and omit its proof.
with two-sided barriers and omit its proof.
Lemma 2.1 Let Z be the RGBM defined by (2) (or(3)). Then, as a Markov process, the stationary distribution 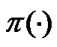 of the process must satisfy the following equation
of the process must satisfy the following equation
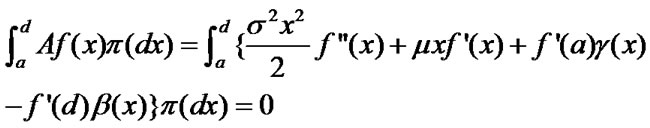 (4)
(4)
where  and
and  which denotes the space of all bounded continuous functions having twicely continuous derivatives on [a,d].
which denotes the space of all bounded continuous functions having twicely continuous derivatives on [a,d].
Proof. See similar argument in [1].
Suppose  be a probability distribution on [a,d] and satisfies that
be a probability distribution on [a,d] and satisfies that
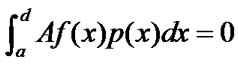 (5)
(5)
for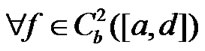 .
.
Define 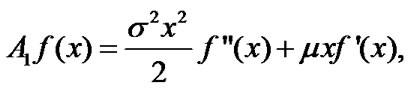 then by (4) and (5) it is equivalent to the following equation (Note that
then by (4) and (5) it is equivalent to the following equation (Note that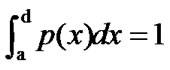 )
)
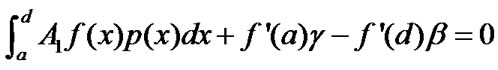 (6)
(6)
where 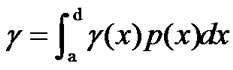 and
and 
On one hand, 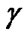 and
and  can be computed by the same method in [5].
can be computed by the same method in [5].
Proposition 2.1 Choose  and
and , then they respectively satisfy the following equations,
, then they respectively satisfy the following equations,

Then we have

Proof. A straightforward calculation.
On the other hand, since  satisfies that for all
satisfies that for all ,
,
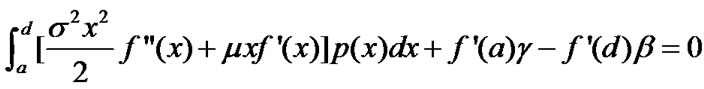
By twice integral changes, the above equation becomes that
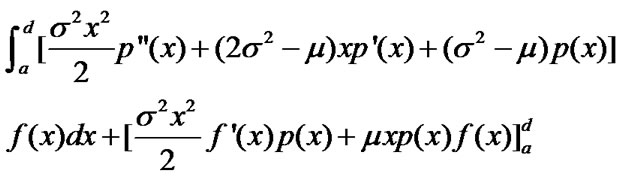
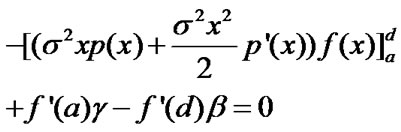
i.e.,
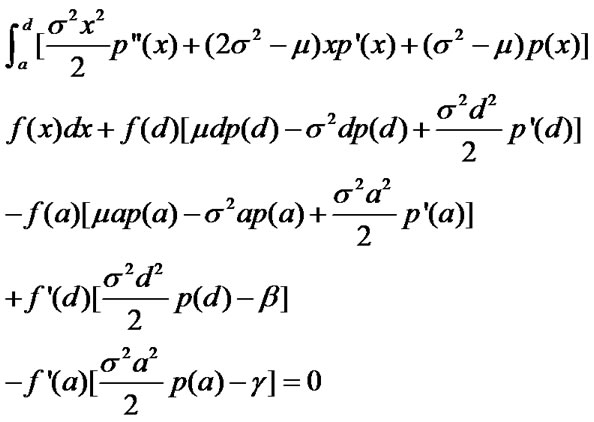 (7)
(7)
Assume that , satisfying that
, satisfying that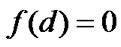 ,
, 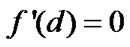 , and
, and 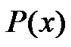 satisfies
satisfies 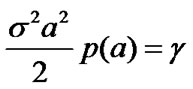 and
and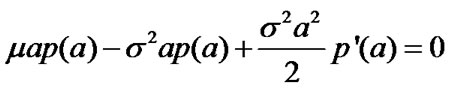 , then it follows from (7) that
, then it follows from (7) that
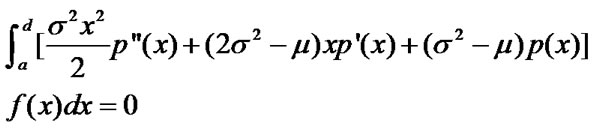 (8)
(8)
Summarizing the discussion, we get the following theorem.
Theorem 2.1 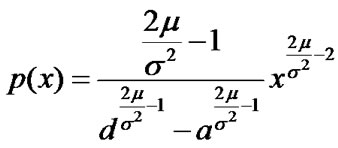 is the solution of
is the solution of
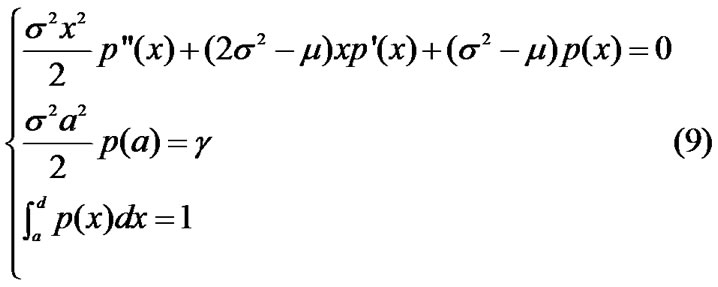
Then for all 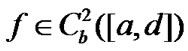 satisfying
satisfying ,
, 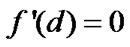 , (5) holds, i.e.,
, (5) holds, i.e.,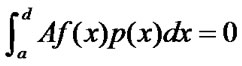 .
.
Furthermore (5) holds for all . This implies that
. This implies that 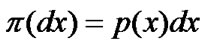 is a stationary distribution of the corresponding Markov process
is a stationary distribution of the corresponding Markov process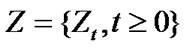 .
.
Remark 2.1 This theorem is a standard application of renewal theorems, so we sketch its proof.
Thus 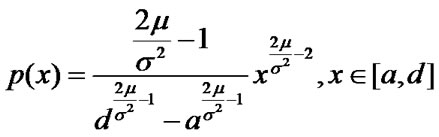 is the density of the stationary distribution of RGBM. Finally we will give an expression for the Laplace transform of the first passage time of RGBM.
is the density of the stationary distribution of RGBM. Finally we will give an expression for the Laplace transform of the first passage time of RGBM.
2.2. On the First Passage Time of RGBM
In this section, we consider equation (2). Let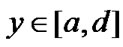 , define the first passage time by
, define the first passage time by 
 with the usual convention
with the usual convention . On the other hand, suppose
. On the other hand, suppose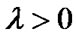 , for
, for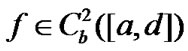 , define a operator
, define a operator
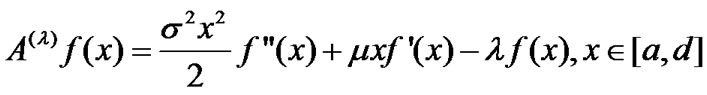
Finally we are going to give the expression of the Laplace transform of .
.
Theorem 2.2. For 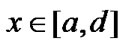 and
and , then
, then
 (10)
(10)
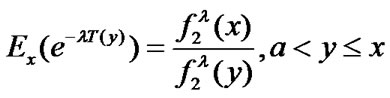 (11)
(11)
where
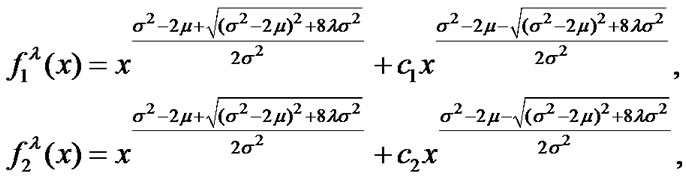
and

Proof. Let for
for . Then applying
. Then applying  formula for
formula for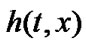 , we have
, we have
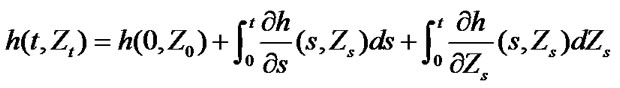

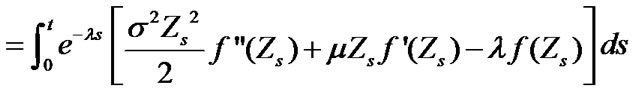

The last equation holds, for 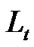 and
and 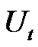 increase only when
increase only when  and
and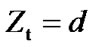 . Let
. Let  be a stopping time and
be a stopping time and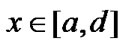 . It follows from martingale optional theorem, that
. It follows from martingale optional theorem, that
 (13)
(13)
In particular, take 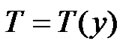 for
for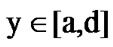 , and note that
, and note that
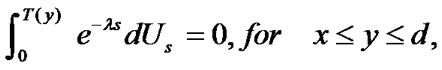
and
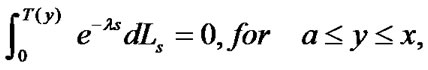
Then
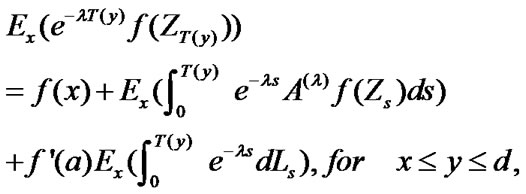 (14)
(14)
and
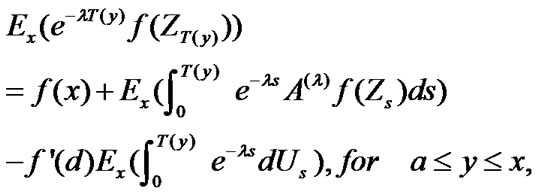 (15)
(15)
Replace 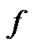 by
by 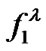 in (14) and by
in (14) and by 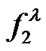 in (15), we immediately get (10) and (11) by
in (15), we immediately get (10) and (11) by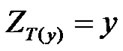 ,
,  and
and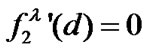 . Thus the Proof of the theorem is completed.
. Thus the Proof of the theorem is completed.
3. Conclusions
This paper studies Reflected Geometric Brownian Motion (RGBM) with two barriers. Both the stationary distribution and Laplace transform of the first passage time of RGBM are derived. The studies for RGBM not only have practical significance, but also give an important result in theory of stochastic process.
4. Acknowledgements
This research is supported by the National Natural Science foundation of China (Grant No.70671074) and the Research Foundation of Tianjin university of Science and technology (Grant No.20080207). The authors would like to thank an anonymous referee for his constructive comments and suggestions on the first version of the manuscript.
5. References
[1] J. M. Harrison, “Brownian motion and stochastic flow systems,” John Wiley & Sons Ltd., New York, 1986.
[2] X. Y. Xing, W. Zhang and Y. J. Wang, “The Stationary Distributions of Two Classes of Reflected OrnsteinUhlenbeck Processes,” Journal of Applied Probability, Vol. 46, No. 3, 2009, pp. 709-720.
[3] S. Asmussen and O. Kella, “A Multi-Dimensional Martingale for Markov Additive Process and its Applications,” Advances in Applied Probability, Vol. 32, No. 2, 2000, pp. 376-393.
[4] S. Either and T. Kurtz, “Markov Processes: Characterization and Convergences,” John Wiley and Sons, New York, 1986.
[5] L. J. Bo, L. D. Zhang and Y. J. Wang, “On the First Passage Times of Reflected O-U Processes with Two-Sided Barriers,” Queueing Systems, Vol. 54, No. 4, December 2006, pp. 313-316.
[6] V. Linetsky, “On the Transition Densities for Reflected Diffusions,” Advances in Applied Probability, Vol. 37, No. 2, 2005, pp. 435-460.
[7] L. Rabehasaina and B. Sericola, “A Second-Order Markov-Modulated Fluid Queue with Linear Service Rate,” Journal of Applied Probability, Vol. 41, No. 3, 2004, pp. 758-777.

