Intelligent Information Management
Vol.2 No.3(2010), Article ID:1486,8 pages DOI:10.4236/iim.2012.23025
Adaptive Method for State Estimation of Sound Environment System with Uncertainty and its Application to Psychological Evaluation
1Department of Circulation Information Engineering, Hiroshima National College of Maritime Technology, Hiroshima, Japan
2Department of Management Information Systems, Prefectural University of Hiroshima, Hiroshima, Japan
E-mail: masuike@hiroshima-cmt.ac.jp, ikuta@pu-hiroshima.ac.jp
Received December 16, 2009; revised January 27, 2010; accepted February 28, 2010
Keywords: Adaptive Estimation, Sound Environment System, Uncertainty, Psychological Evaluation
Abstract
The actual sound environment system exhibits various types of linear and non-linear characteristics, and it often contains uncertainty. Furthermore, the observations in the sound environment are often in the level-quantized form. In this paper, two types of methods for estimating the specific signal for sound environment systems with uncertainty and the quantized observation are proposed by introducing newly a system model of the conditional probability type and moment statistics of fuzzy events. The effectiveness of the proposed theoretical methods is confirmed by applying them to the actual problem of psychological evaluation for the sound environment.
1. Introduction
The actual sound environment system contains uncertainty and it is often difficult to recognize analytically the internal physical mechanism. Furthermore, the stochastic process observed in the actual phenomenon exhibits complex fluctuation pattern and there are potentially various nonlinear correlations in addition to the linear correlation among the time series data.
In our previous study, a digital filter for estimating the state variables of complex stochastic systems was derived by introducing a nonlinear system model in an expansion series of reflecting various type correlation information from the lower order to the higher order between state variable and observation [1]. The conditional probability density function in the expansion series contains the linear and nonlinear correlations in the expansion coefficients, and these correlations play an important role as the statistical information for the state variable and observation relationship.
On the other hand, it is necessary to pay our attention on the fact that the observation data in the sound environment system are often measured in a level-quantized form and contain fuzziness due to several causes. For example, the human psychological evaluation for loudness can be judged by use of 7 levels from 1.very calm to 7.very noisy [2]. However, each score is affected by the human subjectivity and the border between two neighboring scores are vague [3]. Furthermore, the observation data are often measured in a digital level form at discrete times because various kinds of statistical evaluation (e.g., median, mean, covariance, higher order moments, etc.) for these quantized level data become easier if a digital computer is used. Therefore, in order to evaluate the objective sound environment system, it is desirable to estimate the waveform fluctuation of the specific signal for the system with uncertainty based on the quantized or fuzzy observation data.
The Kalman filtering theory and its extended filter are well known in the state estimation problem [4–6]. These theories are originally based on the Gaussian property of the state fluctuation form. Several state estimation methods for nonlinear system have been also proposed by assuming the Gaussian distribution of system and observation noises [7–9]. The actual sound environment often shows an intricate fluctuation pattern rather than the standard Gaussian distribution. Especially, though the unscented Kalman filter (UKF) and particle filter are useful for nonlinear systems, the UKF consideres only the mean and variance of variables, and the particle filter needs very complicated algorithm based on Monte carlo simulation [10,11]. The above previously reported estimation algorithms are assumed accurate system and observation models without containing uncertainty. On the other hand, the actual sound environment systems exhibit complex and unknown system characteristics and often contain uncertainty in the relationship among the state variables and the observation. Thus, it is necessary to improve the previous state estimation methods by taking account of the complexity and uncertainty in the actual systems.
In this paper, based on the quantized or fuzzy observations, an adaptive method for estimating precisely the specific signal for the sound environment system with uncertainty is theoretically proposed. More specifically, first, by adopting an expansion expression of the conditional probability distribution reflecting the information on linear and nonlinear correlation among the time series of the specific signal and the quantized observation as the system and observation characteristics, a method to estimate adaptively the time series of the specific signal is derived. The proposed estimation method can be applied to an actual complex sound environment system with uncertainty by considering the coefficients of conditional probability distribution as unknown parameters and estimating simultaneously these parameters and the specific signal. Next, by introducing fuzzy theory to the uncertainty of the system, the other type of estimation algorithm is derived. The proposed theory is applied to the estimation problem of the psychological evaluation for loudness in sound environment and the effectiveness of the theory is experimentally confirmed.
2. State Estimation of Sound Environment System with Uncertainty
2.1. Estimation Algorithm by Introducing a Stochastic Model
Consider a complex sound environment system with uncertainty that cannot be obtained on the basis of the internal physical mechanism of the system. In the observations of actual sound environment system, the sound pressure level data are very often measured in a digital level form at discrete times. This is because some signal processing methods by utilizing a digital computer are indispensable for extracting exactly various quantities for human evaluation based on these quantized level data.
Let  and
and 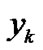 be the input and output signals at a discrete time
be the input and output signals at a discrete time  for a sound environment system. For example, for the psychological evaluation in sound environment,
for a sound environment system. For example, for the psychological evaluation in sound environment, 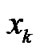 and
and 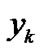 denote the physical sound pressure level and human response quantity for it, respectively. It is assumed that there are complex nonlinear relationships between
denote the physical sound pressure level and human response quantity for it, respectively. It is assumed that there are complex nonlinear relationships between 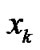 and
and , which are difficult to find a fundamental relationship between them. Since the system characteristics are unknown, a system model in the form of a conditional probability is adopted. More precisely, attention is focused on the joint probability distribution function
, which are difficult to find a fundamental relationship between them. Since the system characteristics are unknown, a system model in the form of a conditional probability is adopted. More precisely, attention is focused on the joint probability distribution function 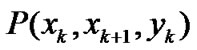 reflecting all linear and nonlinear correlation information among
reflecting all linear and nonlinear correlation information among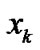 ,
, 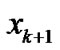 and
and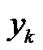 . Expanding the joint probability distribution function
. Expanding the joint probability distribution function 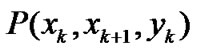 in an orthogonal form based on the product of
in an orthogonal form based on the product of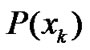 ,
,  and
and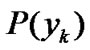 , the following expression can be derived.
, the following expression can be derived.
 (1)
(1)
with
 (2)
(2)
where < > denotes the averaging operation on the variables. The linear and nonlinear correlation information among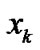 ,
, 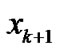 and
and 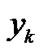 is reflected hierarchically in each expansion coefficient
is reflected hierarchically in each expansion coefficient . The functions
. The functions 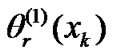 and
and 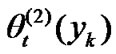 are orthonormal polynomials with the weighting functions
are orthonormal polynomials with the weighting functions 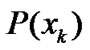 and
and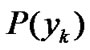 , respectively. These orthonormal polynomials can be decomposed by using Schmidt's orthogonalization [12]. From (1), the conditional probability distribution function
, respectively. These orthonormal polynomials can be decomposed by using Schmidt's orthogonalization [12]. From (1), the conditional probability distribution function 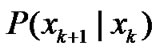 and
and 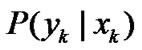 are given as
are given as
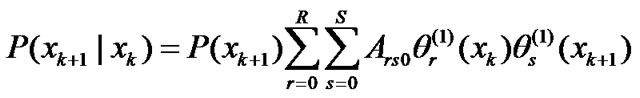 (3)
(3)
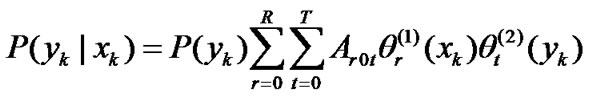 (4)
(4)
Though (3) and (4) are originally infinite series expansions, finite expansion series are adopted because only finite expansion coefficients are available and the consideration of the expansion coefficients from the first few terms is usually sufficient in practice. Since the objective system contains an unknown structure, the expansion coefficients  and
and  expressing hierarchically the correlation relationship between
expressing hierarchically the correlation relationship between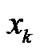 ,
,  and
and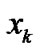 ,
, 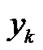 have to be estimated on the basis of the observation
have to be estimated on the basis of the observation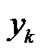 . Considering the expansion coefficients
. Considering the expansion coefficients 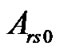 and
and 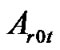 as unknown parameter vectors
as unknown parameter vectors  and
and :
:
 (5)
(5)
 (6)
(6)
where  and
and  are the number of unknown expansion coefficients to be estimated, the simple dynamical models:
are the number of unknown expansion coefficients to be estimated, the simple dynamical models:
 (7)
(7)
are introduced for the simultaneous estimation of the parameters with the specific signal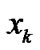 .
.
To derive an estimation algorithm for the specific signal , attention is focused on Bayes' theorem for the conditional probability distribution [12,13]. Since the parameter
, attention is focused on Bayes' theorem for the conditional probability distribution [12,13]. Since the parameter 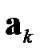 and
and 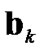 are also unknown, the conditional probability distribution of
are also unknown, the conditional probability distribution of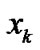 ,
, 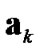 and
and 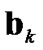 is considered.
is considered.
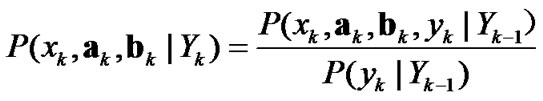 (8)
(8)
where 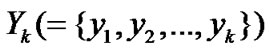 is a set of observation data up to time
is a set of observation data up to time . The conditional joint probability distribution
. The conditional joint probability distribution  can be generally expanded in a statistical orthogonal expansion series:
can be generally expanded in a statistical orthogonal expansion series:
 (9)
(9)
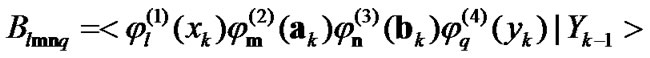 (10)
(10)
After substituting (9) into (8) and expanding an arbitrary polynomial function 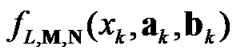 of
of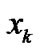 ,
, 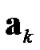 and
and 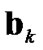 with
with  th order in a series expansion form using
th order in a series expansion form using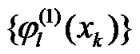 ,
, 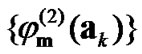 and
and :
:
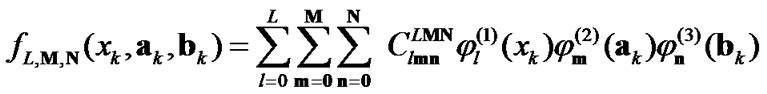
(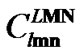 ; appropriate constants), (11)
; appropriate constants), (11)
by taking the conditional expectation of the function  and using the orthonormal condition for the functions
and using the orthonormal condition for the functions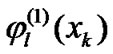 ,
, 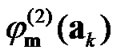 and
and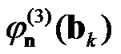 , the estimate of the function
, the estimate of the function 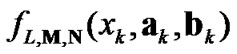 can be derived as follows:
can be derived as follows:
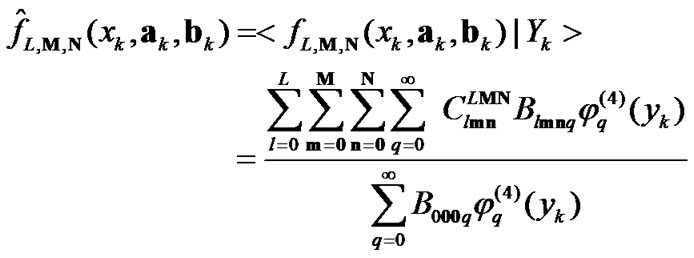 (12)
(12)
The four functions ,
, 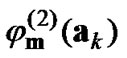 ,
, 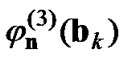 and
and 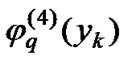 are orthonormal polynomials of degrees
are orthonormal polynomials of degrees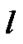 ,
, 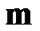 ,
, 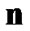 and
and 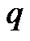 with weighting functions
with weighting functions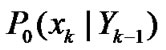 ,
, 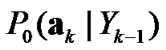 ,
, 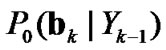 and
and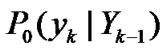 , which can be chosen as the probability functions describing the dominant parts of the actual fluctuation or as the well-known standard probability distributions.
, which can be chosen as the probability functions describing the dominant parts of the actual fluctuation or as the well-known standard probability distributions.
As an example of standard probability functions for the specific signal and the parameter, consider the Gaussian distribution:
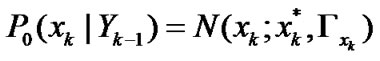 (13)
(13)
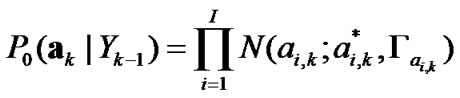 (14)
(14)
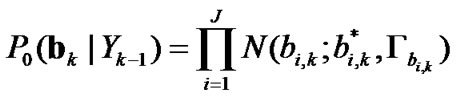 (15)
(15)
with
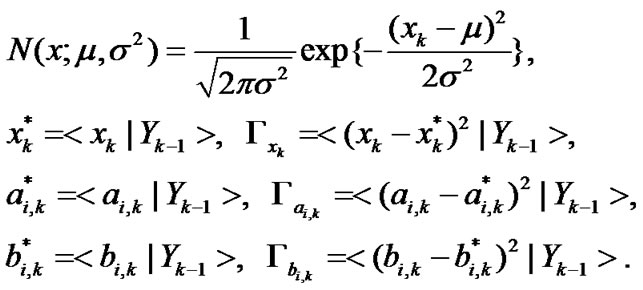 (16)
(16)
Furthermore, as the fundamental probability function on the level-quantized observation, the generalized binomial distribution [14] with level difference interval 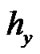 can be chosen:
can be chosen:
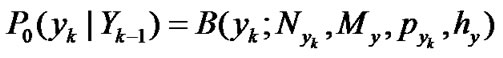 (17)
(17)
with
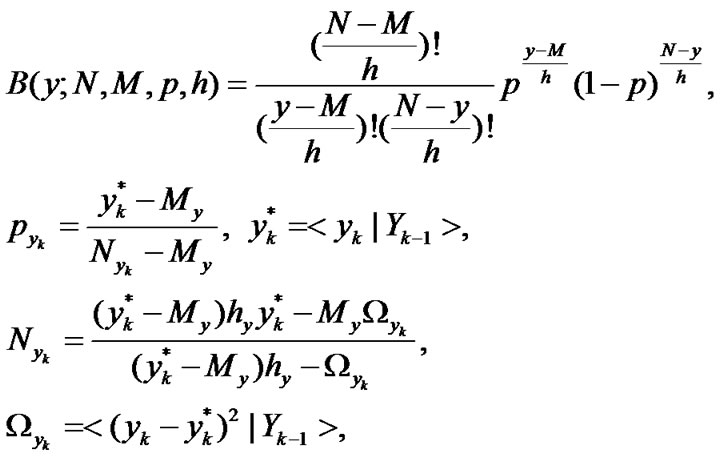 (18)
(18)
where 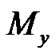 is the minimum level of the observation. The orthonormal polynomials with four weighting probability distributions in (13)-(15) and (17) can be determined as
is the minimum level of the observation. The orthonormal polynomials with four weighting probability distributions in (13)-(15) and (17) can be determined as
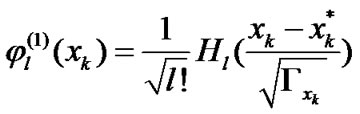 (19)
(19)
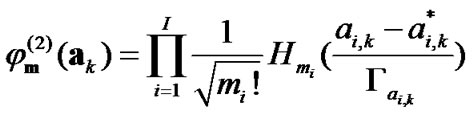 (20)
(20)
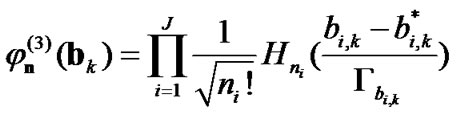 (21)
(21)
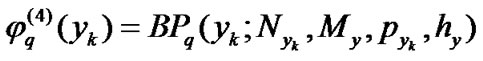 (22)
(22)
with
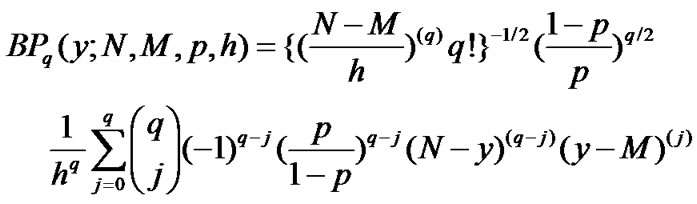 (23)
(23)
where 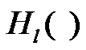 denotes the Hermite polynomial with
denotes the Hermite polynomial with 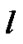 th order [15], and
th order [15], and 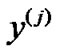 is the
is the 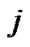 th order factorial function defined by [14]
th order factorial function defined by [14]
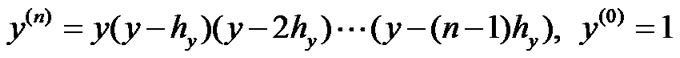 (24)
(24)
Using the property of conditional expectation and (3)(4), the two variables 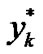 and
and 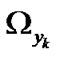 in (18) can be expressed in functional forms on predictions of
in (18) can be expressed in functional forms on predictions of ,
, 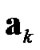 and
and  at a discrete time
at a discrete time  (i.e., the expectation value of arbitrary functions of
(i.e., the expectation value of arbitrary functions of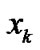 ,
, 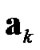 and
and 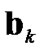 conditioned by
conditioned by ), as follows:
), as follows:
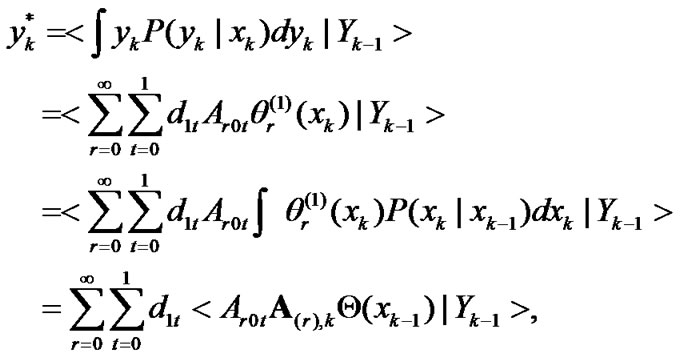 (25)
(25)
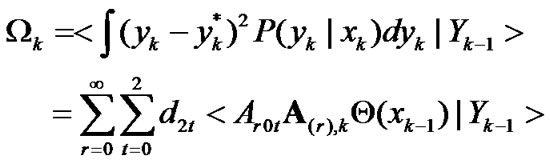 (26)
(26)
with
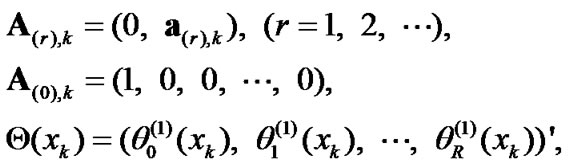 (27)
(27)
where ' denotes the transpose of a matrix. The coefficients 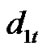 and
and  in (25) and (26) are determined in advance by expanding
in (25) and (26) are determined in advance by expanding 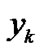 and
and 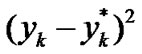 in the following orthogonal series forms:
in the following orthogonal series forms:
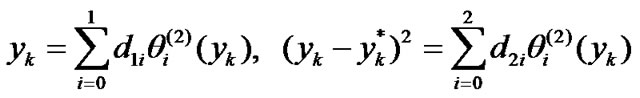 (28)
(28)
Furthermore, using (3) and (4), and the orthonormal condition of 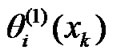 and
and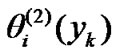 , each expansion coefficient
, each expansion coefficient 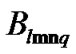 defined by (10) can be obtained through the similar calculation process to (25) and (26), as follows:
defined by (10) can be obtained through the similar calculation process to (25) and (26), as follows:
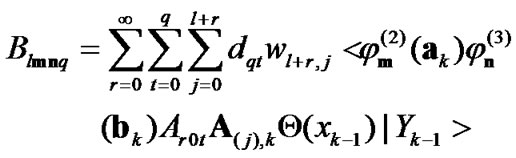 (29)
(29)
where  and
and 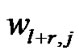 are appropriate coefficients satisfying the following equalities:
are appropriate coefficients satisfying the following equalities:
 (30)
(30)
Furthermore, by substituting the dynamical models of 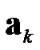 and
and 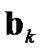 in (7) into (25), (26) and (29), the parameters
in (7) into (25), (26) and (29), the parameters 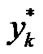 and
and 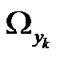 and the expansion coefficient
and the expansion coefficient 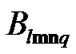 can be given in functional forms on estimations of
can be given in functional forms on estimations of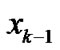 ,
, 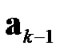 and
and . Therefore, the recurrence estimation of the specific signal can be achieved.
. Therefore, the recurrence estimation of the specific signal can be achieved.
2.2. Estimation Algorithm by Introducing a Fuzzy Theory
In the observations of actual sound environment system, the sound pressure level data often contain fuzziness due to human subjectivity in noise evaluation, confidence limitations in sensing devices, and quantizing errors in digital observations, etc. Let  be fuzzy observation obtained from
be fuzzy observation obtained from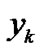 . For example, for the psychological evaluation in sound environment,
. For example, for the psychological evaluation in sound environment, 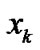 and
and 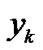 denote respectively the physical sound pressure level and human response quantity for it. Since the system characteristics are unknown, the observation model in a form of a conditional probability in (4) is adopted. Furthermore,
denote respectively the physical sound pressure level and human response quantity for it. Since the system characteristics are unknown, the observation model in a form of a conditional probability in (4) is adopted. Furthermore, 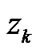 expresses the loudness scores (1.very calm, 2.calm, 3.mostly calm, 4.little noisy, 5.noisy, 6.faily noisy, 7.very noisy) taking the individual and psychological situation into consideration for
expresses the loudness scores (1.very calm, 2.calm, 3.mostly calm, 4.little noisy, 5.noisy, 6.faily noisy, 7.very noisy) taking the individual and psychological situation into consideration for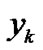 . The fuzziness of
. The fuzziness of  is characterized by the membership function
is characterized by the membership function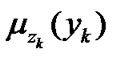 . As the membership function, a standard Gaussian type function:
. As the membership function, a standard Gaussian type function:
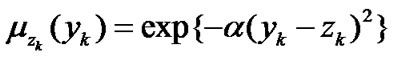 , (31)
, (31)
where  is a parameter, is adopted. Though the parameter
is a parameter, is adopted. Though the parameter 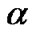 in (31) can be generally given based on the prior information (or, through trial and error), it can be regarded as unknown parameter and estimated simultaneously with the specific signal
in (31) can be generally given based on the prior information (or, through trial and error), it can be regarded as unknown parameter and estimated simultaneously with the specific signal 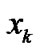 and the parameter
and the parameter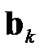 . First, a simple dynamical model for the parameter:
. First, a simple dynamical model for the parameter:
 , (32)
, (32)
is naturally introduced. Next, as the similar manner to (8), by paying our attention to the conditional joint probability density function of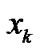 ,
, 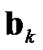 and
and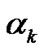 , the following expression is obtained.
, the following expression is obtained.
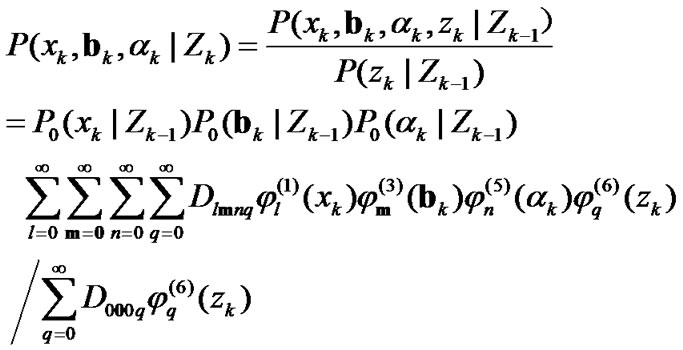 (33)
(33)
with
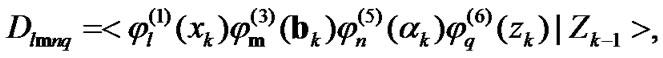 (34)
(34)
where  is a set of fuzzy observation data. The two functions
is a set of fuzzy observation data. The two functions 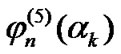 and
and  denote the orthonormal polynomials of degrees
denote the orthonormal polynomials of degrees 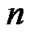 and
and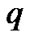 , with the fundamental probability density functions
, with the fundamental probability density functions 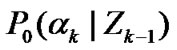 and
and 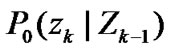 of
of 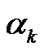 and
and 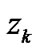 as weighting functions. Based on (33), through the similar calculation process to (12), the estimate of an arbitrary polynomial function
as weighting functions. Based on (33), through the similar calculation process to (12), the estimate of an arbitrary polynomial function 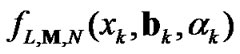 of
of ,
, 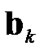 and
and 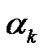 of
of 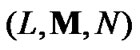 th order can be derived, as follows:
th order can be derived, as follows:
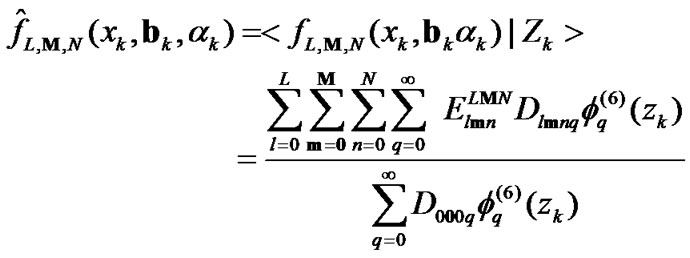 (35)
(35)
All the coefficients 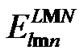 are appropriate constants in the case when the function
are appropriate constants in the case when the function 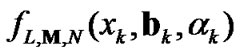 is expressed in a series expansion form similar to (11) using
is expressed in a series expansion form similar to (11) using ,
,  and
and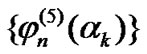 . As concrete examples of the fundamental probability density functions for the parameter
. As concrete examples of the fundamental probability density functions for the parameter 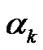 and
and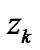 , the Gaussian distribution and the generalized binomial distribution are adopted, respectively:
, the Gaussian distribution and the generalized binomial distribution are adopted, respectively:
 (36)
(36)
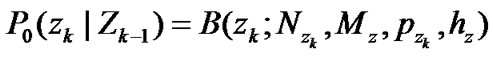 (37)
(37)
with
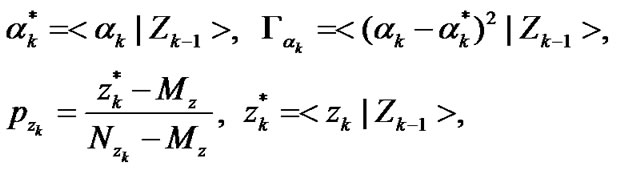
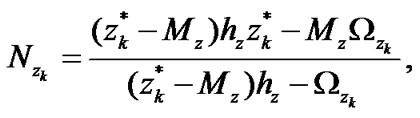
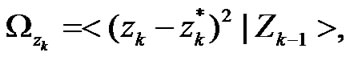 (38)
(38)
where 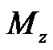 is the minimum level of the observation
is the minimum level of the observation  and
and 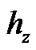 denotes the level difference interval of
denotes the level difference interval of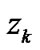 . Then, the orthonormal polynomials with two weighting probability density functions in (36) and (37) can be given as
. Then, the orthonormal polynomials with two weighting probability density functions in (36) and (37) can be given as
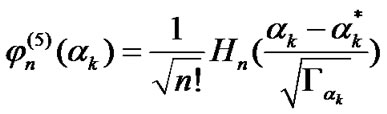 , (39)
, (39)
 . (40)
. (40)
After applying moment statistics of fuzzy events which are generalization of mean and variance of fuzzy events [16], by applying (4), the two variables 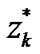 and
and 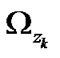 in (38) and the expansion coefficient
in (38) and the expansion coefficient  are expressed in concrete forms, as follows:
are expressed in concrete forms, as follows:
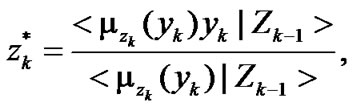 (41)
(41)
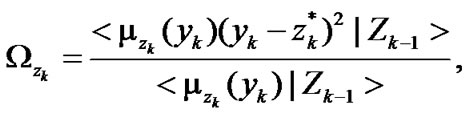 (42)
(42)
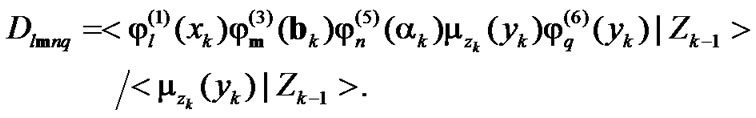 (43)
(43)
Furthermore, by applying (4) and considering orthonormal condition of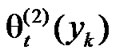 , (41)–(43) can be expressed as follows:
, (41)–(43) can be expressed as follows:
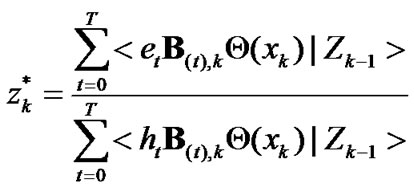 (44)
(44)
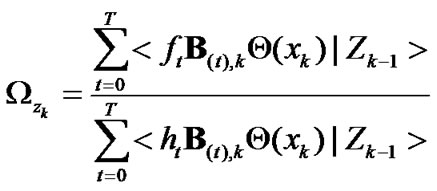 (45)
(45)
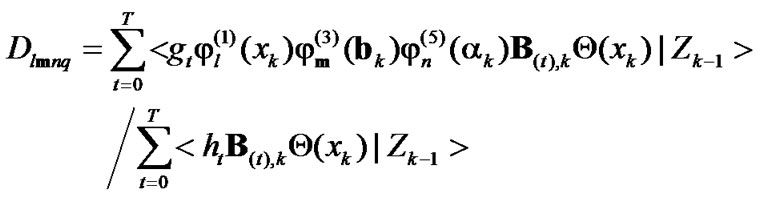 (46)
(46)
with
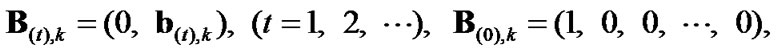 (47)
(47)
where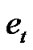 ,
, 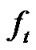 ,
, 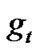 and
and 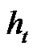 are expansion coefficients satisfying the following relations:
are expansion coefficients satisfying the following relations:
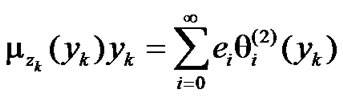 (48)
(48)
 (49)
(49)
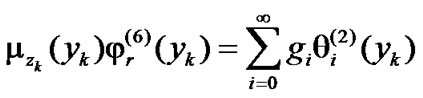 (50)
(50)
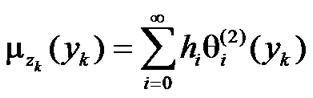 (51)
(51)
The variables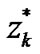 ,
,  and expansion coefficient
and expansion coefficient 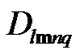 in (44)–(46) can be given by the predictions of
in (44)–(46) can be given by the predictions of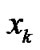 ,
, 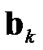 and
and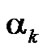 . Furthermore, the following simple system model is introduced instead of (3), for the simplification of the algorithm.
. Furthermore, the following simple system model is introduced instead of (3), for the simplification of the algorithm.
 (52)
(52)
where  is the random input with mean 0 and variance
is the random input with mean 0 and variance , and
, and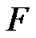 ,
, 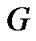 are system parameters. By considering (7) (32) and (52), the prediction algorithm for an arbitrary polynomial function
are system parameters. By considering (7) (32) and (52), the prediction algorithm for an arbitrary polynomial function  with
with 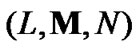 th order can be given as follows:
th order can be given as follows:
 (53)
(53)
Since the prediction of ,
, 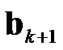 and
and 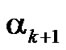 at a discrete time
at a discrete time 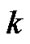 in (53) are given in the form of estimates for the polynomial functions of
in (53) are given in the form of estimates for the polynomial functions of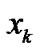 ,
,  and
and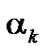 , by combining the estimation algorithm of (35) with the prediction algorithm of (53), the recurrence estimation of the specific signal can be obtained.
, by combining the estimation algorithm of (35) with the prediction algorithm of (53), the recurrence estimation of the specific signal can be obtained.
3. Application to Psychological Evaluation for Loudness
To find the quantitative relationship between the loudness for human and the physical sound pressure level for environmental noise is important from the viewpoint of noise assessment. Especially, in the evaluation for a regional sound environment, the investigation based on questionnaires to the regional inhabitants is often given when the experimental measurement at every instantaneous time and at every point in the whole area of the region is difficult. Therefore, it is very important to estimate the sound pressure level based on the loudness data. It has been reported that the loudness based on the human sensitivity can be distinguished each other from 7 loudness scores, for instance, 1.very calm, 2.calm, 3.mostly calm, 4.little noisy, 5.noisy, 6.fairly noisy, 7.very noisy, in the psychological acoustics [2]. After recording the road traffic noise by use of a sound pressure level meter and a data recorder, by replaying the recorded tape through amplifier and loudspeaker in a laboratory room, 6 subjects (A, B, …, F) aged of 22-24 with normal hearing ability judged one score among 7 loudness scores (i.e., 1, 2, …, 7) at every 5 [sec.], according to their impressions for the loudness at each moment using 7 categories from very calm to very noisy. The mean and standard deviation of the road traffic noise were 71.4 [dB] and 7.23 [dB], respectively. Furthermore, the mean and standard deviation for the loudness scores of each subject, and the correlation coefficients between the road traffic noise levels and the loudness scores are shown in Table 1.
The state estimation method proposed in Subsection 2.1 was applied to an estimation of the time series 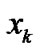 for sound pressure level of a road traffic noise based on the successive judgments
for sound pressure level of a road traffic noise based on the successive judgments  on loudness scores. Figure 1 shows one of the estimated results of the waveform fluctuation of the sound pressure level based on the loudness score by a subject. In this figure, the horizontal axis shows the discrete time
on loudness scores. Figure 1 shows one of the estimated results of the waveform fluctuation of the sound pressure level based on the loudness score by a subject. In this figure, the horizontal axis shows the discrete time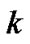 , of the estimation process,
, of the estimation process,
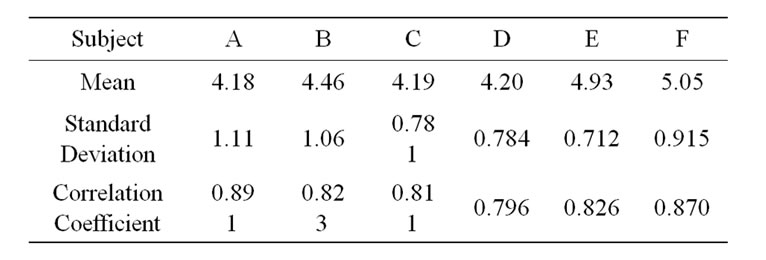
Table 1. Statistics of loudness scores and correlation coefficients between the sound pressure level and the loudness scores.
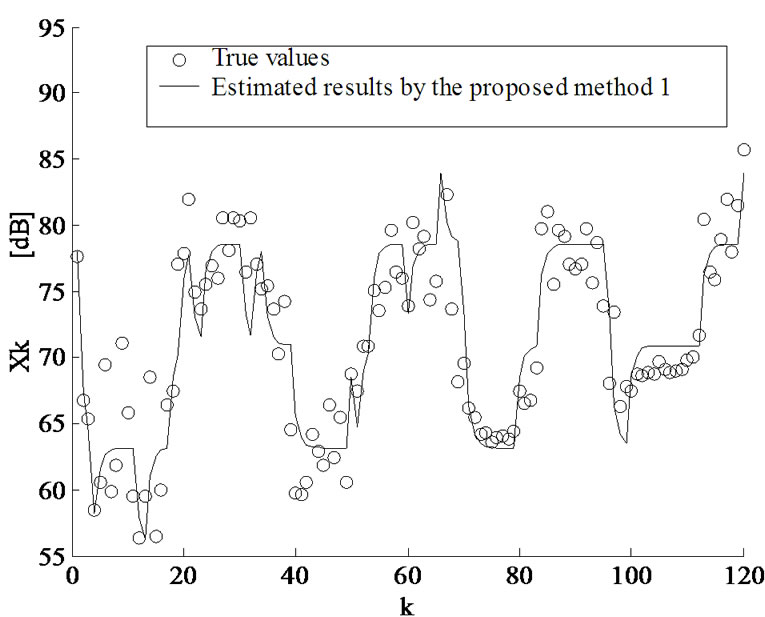
Figure 1. Estimation results of the sound pressure level by use of the method in Subsection 2.1.
and the vertical axis represents the A-weighted sound pressure level (i.e., the sound pressure level measured by use of sound level meter with frequency weight of A-type characteristic). The finite numbers of expansion coefficients 
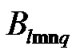 in the proposed estimation algorithm (12) employing the system models of conditional probability type (3) and (4) with
in the proposed estimation algorithm (12) employing the system models of conditional probability type (3) and (4) with 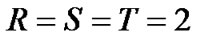 were used in this estimation. In principle, it is expected that the successive addition of higher expansion terms reflecting higher order statistics in the proposed algorithm moves the theoretical estimation closer to the true values. However, higher order statistics based on the finite numbers of observed sample data give us unstable information with less reliability. It remains as one of the future problems to derive a method for determining an optimal order for the conditional probability distribution in expansion series form like (3) and (4).
were used in this estimation. In principle, it is expected that the successive addition of higher expansion terms reflecting higher order statistics in the proposed algorithm moves the theoretical estimation closer to the true values. However, higher order statistics based on the finite numbers of observed sample data give us unstable information with less reliability. It remains as one of the future problems to derive a method for determining an optimal order for the conditional probability distribution in expansion series form like (3) and (4).
One of the estimated results by applying the algorithm proposed in Subsection 2.2 is shown in Figure 2. Furthermore, the estimated processe for the parameter 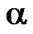 of the membership function in (31) is shown in Figure 3. The estimated parameter converges to a certain value as considering sequentially the observation data. The estimated results of the parameter
of the membership function in (31) is shown in Figure 3. The estimated parameter converges to a certain value as considering sequentially the observation data. The estimated results of the parameter  of the membership function in (31) are shown in Table 2 for all subjects.
of the membership function in (31) are shown in Table 2 for all subjects.
For comparison, the estimated results by the previously reported method [1] and the extended Kalman Filter [6] are shown in Figure 4. The root mean squared error of the estimation is shown in Table 3. It is obvious that the proposed methods show more accurate estimations than the results based on the previous estimation method and the extended Kalman filter. By comparing Table 3 with Table 1, it can be found that the more accurate estimation results are obtained in cases with the larger values of the correlation coefficient between the sound pressure levels and the loudness scores.
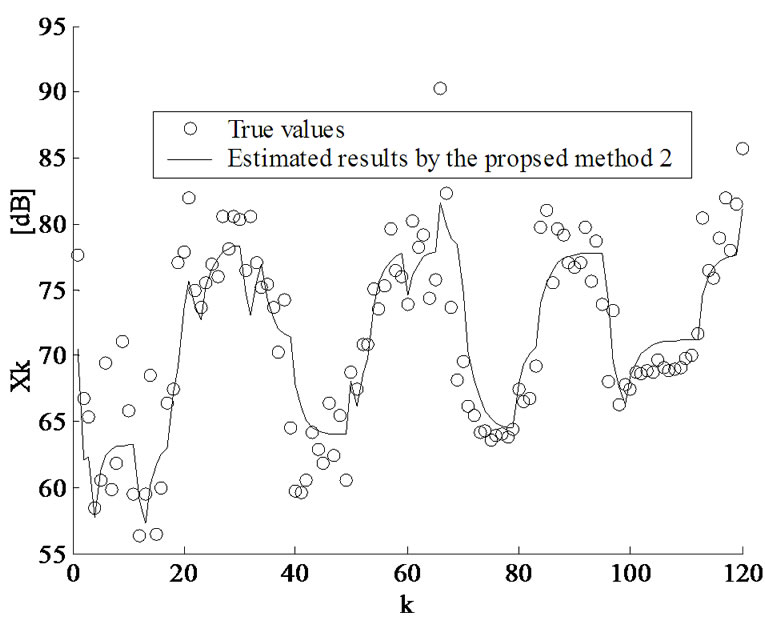
Figure 2. Estimation results of the sound pressure level by use of the method in Subsection 2.2.
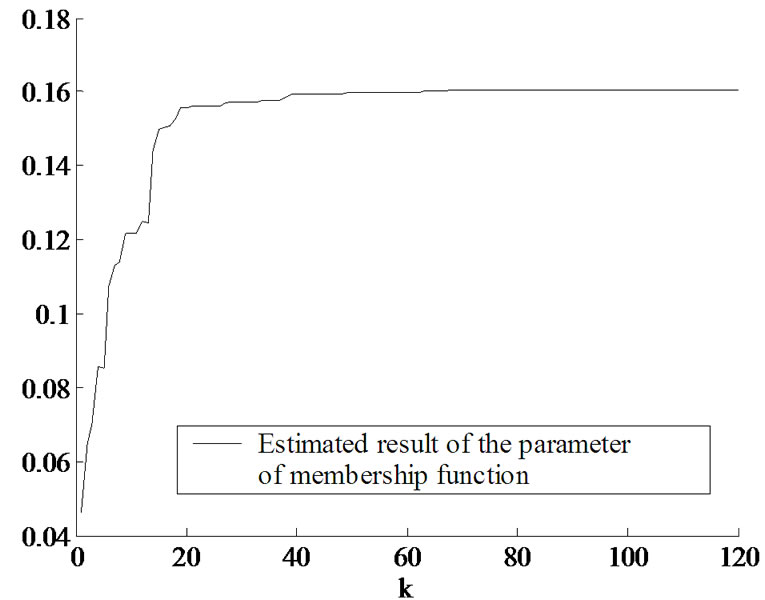
Figure 3. One of the estimation results for the parameter of the membership function.
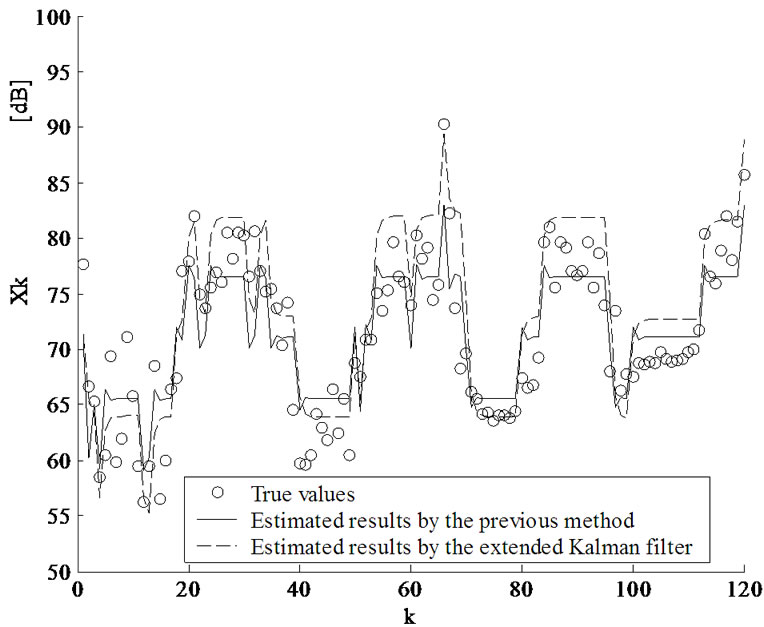
Figure 4. Estimation results of the sound pressure level by use of the previous method and the extended Kalman filter.

Table 2. Estimated results of the parameter of the membership function in (31).
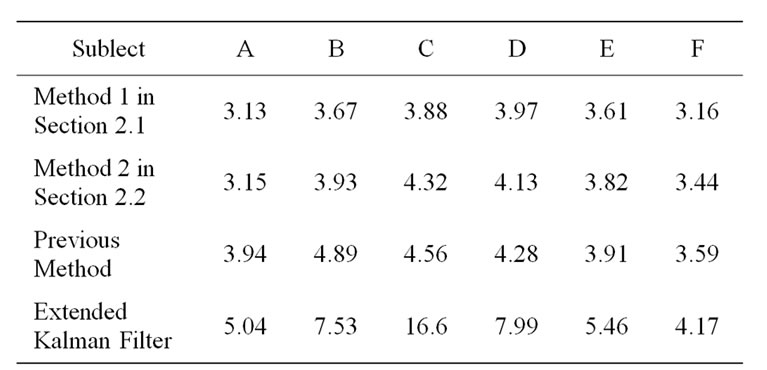
Table 3. Root means squared error of the estimation in [dB].
4. Conclusions
In this paper, based on the quantized or fuzzy observation data, two types of new methods for estimating the specific signal for sound environment systems with uncertainty have been propoesd. The proposed estimation methods have been realized by introducing a system model of conditional probability type and a fuzzy theory. The proposed methods have been applied to the estimation of an actual sound environment, and it has been experimentally verified that better results have been obtained as compared with the results by use of the previous method and the extended Kalman filter.
The proposed approach is quite different from the traditional standard approaches. It is still at early stage of development, and a number of practical problems are yet to be investigated in the future. These include: 1) Application of the proposed state estimation methods to a diverse range of practical estimation problems for stochastic systems with uncertainty. For example, the proposed methods have to be applied to the observation data for human psychological evaluation in many fields in order to estimate the physical quantities. 2) Extension of the proposed methods to cases with multi-dimensional state variable and multi-source configuration. 3) Finding an optimal number of expansion terms in the proposed estimation algorithm of expansion expression type. 4) Extension of the proposed theory to the actual situation under existence of the external noise (i.e., background noise).
5. Acknowledgement
The authors are grateful to Prof. M. Ohta for his helpful discussion during this study.
6. References
[1] A. Ikuta, H. Masuike, and M. Ohta, “A digital filter for stochastic systems with unknown structure and its application to psychological evaluation of sound environment,” IEICE Transactions on Information and Systems, Vol. E88-D, No. 7, pp. 1519–1522, 2005.
[2] S. Namba, S. Kuwano, and T. Nakamura, “Rating of road traffic noise using the method of continuous judgment by category,” The Journal of the Acoustical Society of Japan, Vol. 34, No. 1, pp. 29–34, 1978.
[3] A. Ikuta, M. Ohta, and M. N. H. Siddique, “Prediction of probability distribution for the psychological evaluation of noise in the environment based on fuzzy theory,” International Journal of Acousics and Vibration, Vol. 10, No. 3, pp. 107–114, 2005.
[4] R. E. Kalman, “A new approach to linear filtering and prediction problems,” Transactions of ASME, Series D, Journal of Basic Engineering, Vol. 82, No. 1, pp. 35–45, 1960.
[5] R. E. Kalman and R. S. Bucy, “New results in linear filtering and prediction theory,” Transactions of ASME, Series D, Journal of Basic Engineering, Vol. 83, No. 1, pp. 95–108, 1961.
[6] H. J. Kushner, “Approximations to optimal nonlinear filter,” IEEE Transactions on Automatic Control, Vol. 12, No. 5, pp. 546–556, 1967.
[7] B. Bell and F. W. Cathey, “The iterated Kalman filter update as a Gauss-Newton methods,” IEEE Transactions on Automatic Control, Vol. 38, No. 2, pp. 294–297, 1993.
[8] K. Nishiyama, “A nonlinear filter for estimating a sinusoidal signal and its parameter: On the case of a signal sinusoid,” IEEE Transactions on Signal Processing, Vol. 45, No. 5, pp. 970–981, 1997.
[9] T. L. Vincent and P. P. Khargonekar, “A class of nonlinear filtering problems arising from drift sensor gains,” IEEE Transactions on Automatic Control, Vo. 44, No. 3, pp. 509–520, 1999.
[10] S. Julier and J. Uhlmann, “Unscented filtering and nonlinear estimation,” Proceedings of The IEEE, Vol. 92, No. 3, pp. 401–421, 2004.
[11] G. Kitagawa, “Monte carlo filter and smoother for non-Gaussian nonlinear state space models,” Journal of Computational and Graphical Statistics, Vol. 5, No. 1, pp. 1–25, 1996.
[12] M. Ohta and H. Yamada, “New methodological trials of dynamical state estimation for the noise and vibration environmental system,” Acustica, Vol. 55, No. 4, pp. 199– 212, 1984.
[13] A. Ikuta and M. Ohta, “A state estimation method of impulsive signal using digital filter under the existence of external noise and its application to room acoustics,” IEICE Transactions on Fundamentals of Electronics, Communications and Computer Sciences, Vol. E75-A, No. 8, pp. 988–995, 1992.
[14] M. Ohta and A. Ikuta, “A basic theory of statistical generalization and its experiment on the multi-variate state for environmental noise---A unification on the variate of probability function characteristics and digital or analogue type level observation,” The Journal of the Acoustical Society of Japan, Vol. 39, No. 9, pp. 592–603, 1983.
[15] M. Ohta and T. Koizumi, “General statistical treatment of the response of a non-linear rectifying device to a stationary random input,” IEEE Transactions on Information Theory, Vol. 14, No. 4, pp. 595–598, 1968.
[16] L. A. Zadeh, “Probability measures of fuzzy events,” Journal of Mathematical Analysis and Applications, Vol. 23, No. 2, pp. 421–427, 1968.

