iBusiness
Vol.6 No.2(2014), Article ID:46521,19 pages
DOI:10.4236/ib.2014.62010
Are There Economies of Scale in Highway Maintenance? What about Costs Due to Market Power?
Lawrence Southwick
Assoc. Prof. Emeritus, Department of Finance & Managerial Economics, School of Management, University at Buffalo; Formerly Councilman & Former Comptroller, Town of Amherst, NY, USA
Email: ls5@buffalo.edu
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 11 April 2014; revised 12 May 2014; accepted 28 May 2014
ABSTRACT
The object of this paper is to determine whether there are economies or diseconomies of scale in highway maintenance and whether higher concentration levels/greater market power across the governments involved in highway maintenance results in higher or lower cost levels. The data used come from New York State municipalities. New York is divided into Towns and Cities that added together give the total land area for the State. There are also Villages that are located in one or more Towns. All of these government entities may own and manage/maintain highways. The results are that 1) there are significantly U-shaped average cost curves, but the differences in average costs between communities with lower numbers or higher numbers of lane miles than the most efficient are not very great and 2) there are both substantial and significant increases in average costs when market power is greater. Thus, making the case for mergers of communities is more difficult and such mergers would be more problematic.
Keywords:Scale Economies, Market Power, Municipal Highways

1. The Theories
One of the theories of voter behavior is that voters look at neighboring jurisdictions to compare how efficiently these operate relative to their own local officials and vote accordingly. Geys [1] shows that the result of such voter scrutiny will be costs of operation that are closer across neighboring municipalities than would otherwise be the case. Jiminez & Hendrick [2] argue that consolidation is needed so that considerations of conditions across areas are taken into account.
Another theory is that municipalities act so as to minimize the average cost per capita. This would seem to imply that the size of the municipality would tend toward the most efficient. That efficient size could be accomplished by appropriate mergers or divisions of municipalities. However, this neglects the incentives facing the government unit employees; if they gain from being in larger units they are likely to promote mergers while if they are better off in small units they are likely to oppose such mergers. This will be independent of the benefits to the citizenry. It is worth questioning whether the actual incentives facing the local governments will or will not drive them to optimal sizes.
Voters are likely to choose among possible local governments in their location decisions by comparing the values/levels of the services provided by each relative to the costs imposed by each due to the provision of those services. This is the Tiebout [3] hypothesis. The result is that communities which have a high service value to cost ratio will tend to grow. Those with a lower service value to cost ratio will tend to decline.
Another way of looking at the problem is that the choice facing local government officials is to maximize property values in the community. If they choose the amount of services wisely and keep the cost within reason, the result will be that more people will tend to move to the community and fewer will leave. If they choose unwisely, the opposite will occur. By having more people come and fewer leave, the result will be an increase in property values. This will particularly be the case for land values since the area of the community is fixed, absent mergers or divisions.
Another aspect of choice among communities is differing preferences on the part of the people choosing to move there. People entering will pick their community according to how close it is to their preference. This suggests that the sizes of communities may matter less than the desired level of services that are provided to the residents. The result is that one cannot simply compare the cost per capita across communities in order to determine efficiency.
Various communities might well choose different mixes of service and taxes in order to appeal to differing market segments. Families with children for example might well look to live in communities where there are high levels of schooling. Older people might not care as much about the quality of the schools1.
The elected officials, however, will tend to pick market segments which result in higher property values. By choosing the market segment to serve there will be a competitive effect. If the gains are seen to be higher in one market segment more government officials will aim for that segment. This competition will tend to drive out excess profits and will result in all of the segments being equally profitable.
2. Introduction
Highways, also called roads or streets, are owned by most local governments. The governments may have built the highways or the highways may have been given by the owners to the municipality to be maintained by that municipality. Typically, local highways come from developers who have constructed them and seek to have the municipality take over and maintain them thereafter. Such highways usually are required by the municipality to be constructed to specifications set by the municipality so as to keep maintenance costs to a minimum while assuring adequate traffic flow, at least for some period of time. However, both usage and age result in deterioration, causing a need for maintenance and repair.
The developer frequently builds a new highway using his money with an eye to creating accessible buildable lots for people to buy. That road then makes his property sufficiently more valuable to overcome the cost of its building. Presumably, the resulting increase in taxable property value then generates enough future taxes from the buyers to more than cover the future cost of maintaining the highways that are donated in this fashion. Thus, both the developer and the local government (and thereby, the current taxpayers) benefit.
Both water and sun are enemies of highways. The water through erosion or through freezing and thawing breaks up the pavement. The sun dries out asphalt and induces deterioration. If sufficient deterioration occurs, the highway will need to be rebuilt at much greater expense than if it is more frequently restored. Thus, there is a tradeoff between the frequency of repair and the cost of the repair2. Additionally, there is a need to maintain drainage facilities and the growth products such as grass and leaves on abutting property that also belongs to the municipality along with the paved area3.
A municipality has several options as to how to maintain their highways. First, the choice most often made is to perform the work by employees of the municipality. Second is to contract with another municipality (usually adjoining) to do the work and to be reimbursed by the municipality doing the contracting out. Third, the municipality may contract with private contractors to do the work required at a (usually) bid price.
It can generally be inferred that, if the municipality has very low personnel expenditures for maintaining its roads relative to its road mileage, it must be contracting out to someone else the actual work to be done. The payment mechanism may be such that, if a Village contracts with a surrounding Town, the payment may not show up in the Village’s expenditures because the Town may simply collect a tax from the whole Town, including the Village, for covering its costs. If the contracting is with a private contractor, the expenditure will show up the Village’s financial report. Of course, the arrangement with the Town may also be on a cash basis. Examples of such contracting with the surrounding Town in New York State include Farnham Village in Brant Town in Erie County and Brushton Village in Moira Town in Franklin County4.
There are at least two possible ways to handle the data for the municipalities that contract out their highway maintenance. Presumably, they do so because it is less expensive than performing the work in-house. We can refer to this as providing the service while not producing the service. If the contract is with a private firm, we may assume that the municipality is achieving the economies of scale in production that it would not achieve by producing the service in-house. It may also benefit because municipalities may be inherently less efficient than private firms due to their differing incentives. Thus, it seems appropriate to exclude these from the data set since the object is to determine whether there are economies of scale in production.
There are more possibilities than typically meets the eye at first glance. A Village may contract with an adjoining Town of which it may be a part, it may contract with a nearby City, it may contract with the County in which it is located, or it may contract with private vendors for some or all of the highway related services. Altmar Village, located in Albion Town in Oswego County, chooses to contract with the surrounding County.
Other possibilities include a County contracting with a Town to provide maintenance services for a County highway or a Town contracting with a Village or a Town contracting with a neighboring Town. Erie County contracts out the maintenance of some of its highways, particularly snow removal, to the Towns within which those highways run5. Presumably, it does that to generate profits through receiving more money per lane mile from the State for maintaining some State roads than it pays the Towns for maintaining its own (County) roads6.
Because the objective of this paper is to look at production economies, Villages which choose to contract the service out need to be eliminated from the data set. If they produce their own service, the Town or Towns in which they are located need to have the population of the Village that is served this way subtracted from the Town’s population so as not to double count.
There are several reasons for believing that there may be or not be economies of scale. Much of what passes for reasoning in this is a simple belief, not supported by empirical analysis, that larger is always less expensive. If one believes this, then it would follow that mergers of municipalities would always be cost-saving. However, it does not always work out that way. Let us consider, for example, the issue of “span of control”. That is a management concept that suggests that the number of people one supervisor can adequately supervise is limited. If that is so, it would necessarily imply that increasing the size of the government unit would necessitate an increase in the number of levels of management.
Let us suppose that the span of control for one supervisor is N subordinates. Since this is just an example, we’ll further presume that that is true for all levels of supervisors. Now let’s make the assumption that the actual workers on the road at the lowest level are M persons per lane mile. This implies for a given community of L lane miles, the number needed of these workers is LM. Let this value be A. The first level of supervisors, S1, will be A/N. If S1 > 1, the number of second level supervisors, S2, will be A/N2. If S2 > 1, the number of third level supervisors, S3, will be A/N3. If S3 > 1, the number of fourth level supervisors, S4, will be A/N4. This can be continued until we reach a point where S(i) < 1. The total number of supervisors will be S1 plus S2 plus S3 plus S4 etc. The total number of employees will be A + S1 + S2 + S3 + S4 … Assuming only 4 levels of managers, the total number of employees would be A [1 − (1/N)^4 ]/[1 − 1/N]. For a span of control of 5, the number of employees would be A [1.248]. As the size of the workforce (lowest level) increases, the total employment increases from 20 percent more than the lowest level number of workers and approaches 25 percent more than the lowest level workers. Of course, this is true only of cases where exact numbers of supervisors rather than a greater proportion are needed. With 3 workers and one supervisor, for example, the total workers would be 33 percent more than the number of lowest level workers. In the case of a lowest level of workforce of 27, the number of first level supervisors would be 6, the number of second level supervisors would be 2, and a supervisor would be needed on the third level. This would result in a total workforce of 36, or 33 percent above the number of lowest level workers.
It is also the case that the pay for supervisors nearly always increases as we move up the steps from S1 to S2 to S3 to S4, etc. A typical ratio of pay, as one moves up the ladder, may well be about 25 percent per step. The lowest level worker would be paid W, the first line supervisors would be paid 1.25 W, the second level supervisors would be paid 1.5625 times the lowest level, etc. By the fourth level of supervisors, they would be paid 2.44 times the lowest level. Now, we can calculate the total payroll for the workers and supervisors. The general result is Payroll = AW [1 − (s/N)^4]/[1 − (s/N)]. Assuming the 4 levels, span of control of 5, and 25 percent increase in wages at each level, the result is Payroll = AW [1 − (1.25/5)^4 ]/[1 − (1.25/5)] or Payroll = 1.328 AW. This is a substantial diseconomies of scale effect; keep in mind that that A is directly proportional to lane miles7. It also seems, from casual observation, that larger communities tend to pay higher wages generally, thus adding to the diseconomies effect.
What about the theoretical possibility that there are actually economies of scale? As an example, larger work groups may offer increasing specialization. This would allow more learning about the job and consequently greater efficiency. The purchasing of supplies offers such an example. However, in New York State, the state itself takes bids for a large number of supply items. The various municipalities are allowed to buy from the list of supplies for which the bids are taken. Because the bidders are aware from past experience and data provided by the state of how much this offer has been taken up by the municipalities in the past, this helps make the potential suppliers aware of how profitable winning the bids may be. This larger market, available to even the smallest municipalities, reduces the likely disparity among municipalities in what they pay for supplies and equipment. This reduces any possible economy of scale from this mechanism.
Another way in which there could be economies of scale is if the additional layers of management increased productivity by more than they increased costs. Thus, those at the higher levels, while being compensated at higher rates, produce more than their wages represented. However, this suggests that there is not a competitive market for managers so that the most productive people are not paid as well as their performances would justify. Since the market for the most productive would be expected to be more than simply local, this seems hard to explain.
The other major question to be studied is whether there are market power effects. Since there are, in most NY communities, labor unions representing the workers, this really is mostly a question of whether the unions are able to take advantage of market power to raise wages or introduce efficiency reducing work rules, thus increasing the number of workers. Either, of course, would increase costs. Since the taxpayers have incentives to choose less costly municipalities in which to live, the unions will have to take the nearby municipalities into account in negotiating wages; if they seek too much, they will reduce the value of property in their own jurisdiction and thus limit their possible future compensation.
For the family choosing where to live, the tax costs are a factor as well as is the distance to work and shopping. Over time, both of these will tend to migrate toward their customers and suppliers. That is, for example, if a suburb gains population, it will attract new shopping venues. New employer firms will also be attracted to be closer to their workers so as to make their commuting easier. Higher property values will result and will reduce the necessary taxes.
The consequence of a union increasing wages and thereby costs by too much can be seen to have increased competitors. This will tend to limit the capability of the union to control wages. In fact, the negotiators on union wages in the municipalities will very often focus on the wages that have been negotiated in neighboring communities, tending to aim for a wage level that is in some relation to the average of the neighbors8. The result will be wages that tend to be similar in nearby communities.
Because municipalities within counties appear to have more in common that do municipalities across counties, and because commuting across county borders tends to be more costly than within county commuting, the county is selected as unit within which most cross-community competition takes place. Thus, it is the area within which the market power is measured for purposes of this paper. While imperfect, this may well capture at least some of the market power effects.
3. Data
Because each state has laws that are different from other states as well as having different weather conditions, it is worthwhile taking data from only one state9. The issue with which we are concerned is the question of whether there are inherent differences in costs over different sized municipalities. Clearly, the wages paid will differ across states, typically by more than they will differ within a state. Further, the rules concerning maintenance will differ; in Eastern states, for example, the roads often have narrower shoulders than do those of Midwestern states.
I began with 21,608 observations, including Cities, Towns and Villages, over a period of 14 years from 1993 to 2006. The data come from New York State Dept. of Transportation10. New York City is not included because of its substantial differences with other municipalities. The data for expenditures come from the NYS Comptroller’s Office11. Some 344 of these observations had no financial data, typically because the information was not received by the Comptroller’s Office in timely fashion or because there was no mileage data available for the highways in the municipality. There were 932 Towns, 61 Cities, and 554 Villages in 2006. These numbers have varied a bit over the years.
Ultimately, after also deleting several double observations where a Town is coterminous with a Village and keeping only one of the pair as well as deleting communities where nothing or very little relative to mileage was spent on the roads, I ended up with 20,711 observations.
Some Towns have Villages or parts of Villages within their borders. If a Village chooses to perform its own road maintenance, its population should not and will not be counted as part of the Town’s population with regard to the Town’s road maintenance. Nor will its road miles be included with the Town’s miles. On the other hand, if the Village chooses to contract with the Town to have the Town do the work, the population of the Village should be included with that of the rest of the Town. Further, the mileage of the roads owned by the Village in that case should be added to the Town’s own road mileage12.
Consider, for example, the Town of Greece. It has a population of about 92,000. It has no Villages within it. Compare that with the Town of Greenburgh that has a population of about 90,000. These would at first blush seem to be about the same size. However, there are six Villages within Greenburgh, all of which maintain their own roads. These are Ardsley, population 4800, Dobbs Ferry, population 11,200, Elmsford, population 4700, Hastings-On-Hudson, population 7800, Irvington, population 6600, and Tarrytown, population 11,400. When these are subtracted from Greenburgh, the result is a population served by the Greenburgh highway department of 43,500, less than half that of Greece.
There are several parts to highway maintenance in New York State. They include 1) snow plowing and salting of their roads to prevent slipperiness as well as blockages, 2) repair of roads such as filling potholes or resurfacing the roads, 3) maintaining appropriate drainage by cleaning drains and ditches of the roads and 4) rebuilding roads, frequently including better drainage. Repairs also include signage, mowing, leaf collection, and striping, where warranted. Because these are all budgeted together, we cannot readily separate the functions out to find economies for each13.
Municipalities in New York State typically have unions for municipal employees. This is essentially mandated by the State in a way that makes such organization very easy. Further, the rules on bargaining give more power to such unions than would be the usual case in the private sector14.
Because of the employee unions that do bargaining for salaries and a variety of benefits, the costs of the employees will be determined by the effective capabilities for that bargaining. It is normally the case that having fewer alternatives for the ultimate customers, the residents, will give a greater advantage to the employee unions. That is, the greater the concentration of union power, the greater the likely result in terms of employee costs. The actual effect of this must necessarily be taken into account along with the road mileage.
Retirement benefits for the various local government employees are set by the State and are funded through assessments on the local governments in accord with their actuarially expected future costs. The fund thus created is managed by the NY State Comptroller, an elective position, which is therefore subject to political influences. However, political events such as giving employees an extra two years work credit15, apply to all Cities, Towns and Villages and so will not show up in the New York State data except as an effect of the year.
A particular municipality may have weather conditions that differ from others in a systematic way. For example, a Town located along Lake Erie or Lake Ontario is likely to have more lake effect snow that a similar Town located away from such large lakes. Endreny and Doherty [5] point out that the Atlantic coast receives about 30 inches of snow per year while along Lakes Erie and Ontario the snowfall is from 90 to 200 inches per year and the Tug Hill Plateau gets about 300 inches. It is useful therefore to include dummy variables for each municipality in order to remove these influences from the results.
4. Prior Research
Grossman, Mavros, and Wassmer [6] make the interesting suggestion that public sector expenditures should add to property values in the jurisdiction. They go on to find that large cities produce more services than would be efficient. This may be from either diseconomies of scale or aggrandizement of the leaders similar to what is sometimes seen in certain private corporations.
A number of papers have sought to find whether there are economies of scale in regard to roads. However, many of these use forms of the equations estimated that require returns to scale over the entire range that are either always increasing or always decreasing. For example, Berg’s 1972 article [7] appears to fall into this category. Christofferson & Larsen [8] also simply assume declining AC curves. Goldin [9] also effectively assumes declining average costs for roads. The Bracknell Forest Council [10] appears to assume, without evidence, that there are economies of scale in highway maintenance. However, because most of the work is contracted out, this is not important for them.
Berg [7] found that highway costs were directly related to the level of land access provided and inversely related to the total road mileage. However, he only had a single coefficient related to mileage and so could not possibly find economies and diseconomies at different sizes. Levinson & Yerra [11] also find, using a single coefficient estimation, that there are economies of scale. However, they also argue that larger organizations have more bureaucracy as well as problems with span of control. Holcombe and DeEdgra [12] found that highway expenditures were not significantly related to population and population squared16.
Another method of estimation is DEA (Data Envelopment Analysis, a linear programming method)17. This has been used in a number of studies, with mixed results. Amatatsu, et al. [15] , indicate a finding of economies of scale that decrease with scale, thus allowing for possible U-shaped cost curves, although that is not explicitly estimated. Afonso and Fernandes [16] use expenditures to measure both inputs and outputs, a process which cannot provide the conclusions desired here. Benito, Bastida, and Garcia [17] use DEA for several services for 31 municipalities and find little of significance. Brynes, Dollery and Lopez [18] use DEA for Australian roads and find no significant differences to scale. Rouse and Putterill [19] use DEA and find significant non-increasing returns to scale, although they had earlier [20] found increasing returns to scale. Geys and Moesen [21] use both DEA (and FDH) and econometric approaches, and find that the efficiency results are correlated.
De Palma, et al., [22] cite New Jersey Dept. of Transportation studies in 2006 and 2007 as showing economies of scale in road maintenance (page 458). Using 45 data points, they estimated the following equation:
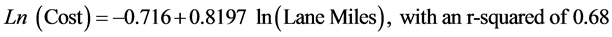 .
.
This, it is argued, shows economies of scale. We can use the information provided to find that the standard error of the coefficient on ln(Lane Miles) is 0.086. If that coefficient is actually greater than 1.0, however, there would be diseconomies of scale. The coefficient is 2.096 standard errors from 1.0 while the 95% (2 tailed) t-test requires it to be more than 2.014 standard errors away. Thus, it barely satisfies the 95% test. Further, however, the issue here for the purposes of this paper is that it is impossible to have, with this equation, non-constant returns to scale.
Williams [23] looks at population density and generally finds diseconomies of scale for highways. Holcombe & Williams [12] use two scale variables, population and population squared. Since both coefficients as estimated were not significant, they conclude that neither economies nor diseconomies of scale exist for highways. However, that conclusion is not warranted, given the results. Weicher [24] used population and density and found that there were diseconomies of scale. Staley [25] refers to a number of papers that find diseconomies of scale in consolidation of governments. He proposes more decentralization.
General government consolidation is one way of achieving economies of scale, if such economies exist. Dollery, Brynes and Crase [26] find, using Australian data, that amalgamation has had adverse (increasing) effects on expenditures. Faguet [27] argues that decentralization improves performance. Feiock [28] argues that local officials may desire consolidation in order to advance their careers. Humplink and Moini-Araghi [29] find empirically that decentralization produces the most efficiency gains. Reingewertz [30] found that amalgamations resulted in municipal expenses going up, taxes going up, and debt per capita going up. Staley, et al. [31] reviewed the available literature and found that significant gains to consolidation were unlikely. Couch, et al. [32] also did this and also found no apparent gains from consolidation. Hicks & Bohanon [33] used regressions with tax rates as the dependent variable. This is a suspect method because tax rates depend on property values as well as on costs.
Some researchers have studied the issue of possible U-shaped average cost curves. Geys, B., Heinemann, F. & Kalb, A. [34] found, using translog estimation for 1021 German municipalities, that very small communities exhibit economies of scale with the most efficient being between 6000 and 9000 population. However, Link [35] uses translog estimation and finds economies of scale in Germany. Southwick found U-shaped average cost curves for police [4] and for general overhead spending in local governments [36] .
Another issue is whether competition matters. Sjoquist [37] found that the more governments which were available to compete with the central city, the lower were the expenditures. Lisk [38] found that having competitive markets and competition for highway maintenance made a great deal of difference in the resulting costs. Southwick [4] and [36] also found that greater market power resulted in increased costs.
5. Estimation
There are several the possible forms for the equation to take; the quadratic and the translog are the two that will be used here. The objective is to relate the cost per lane-mile to size variables and market power variables.
It would also be feasible to look at centerline (road) miles instead of lane miles. However, the costs appear generally to be mostly due to the number of lane miles; also with a correlation of 0.994 between lane miles and centerline miles within the sample set, the effects would be difficult to separate statistically. Typically, for the municipalities and roads involved, the number of lane miles would be twice the number of centerline miles. There are, occasionally, single lane roads or roads with more than two lanes. Most of the multi-lane roads, however, are owned either by counties or the state. The mean number of lane miles in the sample is 93.4 and the mean number of centerline miles is 46.8.
A number of other questions will also be considered in the following research. While the two main issues are whether there is a U-shaped average cost curve and, if so, what the minimum point is and whether greater market power results in higher costs, there are also other questions of potential interest.
6. Translog Equations
The first estimate is ordinary least squares with the dependent variable as the natural log of the cost per lane mile and the independent variables as the natural log of the lane miles (LLM) and the square of the log of the lane miles (LLM*LLM). There are 20,711 observations used. The result is given in Table 118.
Each of the coefficients in the Table 1 estimation is highly significant. The result of this equation is that the minimum cost is achieved at 232 lane miles. The cost at that number of lane miles would be, on average, $8058 per lane mile per year.
It is useful to determine how sensitive the per lane mile cost is to the number of lane miles. Therefore, I took the optimal number of miles and added 50 percent to that number and subtracted 50 percent from that number to get the costs of larger highway departments and smaller highway departments. The results in this case were costs of $8102 and $8187 per lane mile. That is only 0.55 percent higher and 1.61 percent higher, respectively. Thus, while the result is significant, it does not appear particularly substantial.
Another view can be had by including dummy variables for each community so as to take out of the regression the individual community effects. The result is in Table 2, for the random effects model19.
Table 1. Translog estimation—OLS.
Adj. R-squared = 0.06289; F-Test = 695.97, Prob. = 0.
Table 2. Translog estimation—random effects.
The result of this equation is that the minimum average cost per lane mile is found at 128 lane miles. That average cost is $8113.
A municipality with 50 percent more miles, or 192, would have average costs of $8181, or 0.83 percent more. A municipality with 50 percent fewer miles, or 64, would have average costs of $8312, or 2.5 percent more than the overall average. Again, this estimate, while highly significant, is not very substantially different from the optimal.
The final estimate for this will be a frontier estimate. That is a regression that uses information on actual costs incurred in some cases to infer the possibility that such a cost is possible. (Basically, the half-normal distribution of residuals is assumed.) Using the same variables, the result is given in Table 3.
Table 3. Translog estimation—frontier.
The result of this equation is that the minimum average cost per lane mile would be achieved at 253 miles. That average cost would be $4571.
Increasing the mileage by 50 percent and reducing it by 50 percent give cost figures of $4594 and $4639, respectively. These are increases of 0.50 percent and 1.48 percent from the lowest possible value.
It is interesting to compare the average of $8113 per lane mile with the possible minimum of $4571. The best possible is about 44 percent below the average. However, we should not draw too strong an inference from this result. It is possible that maintenance of either roads or equipment may be deferred for a time by some communities, resulting in a lower measured cost for a given year but not a lower true cost since deferred maintenance is likely to result in greater costs when the deferred maintenance is finally done.
7. Quadratic Equations
The first quadratic form estimate is ordinary least squares with the dependent variable as the cost per lane mile and the independent variables are the number of lane miles (LM) and the inverse of the number of lane miles (1/LM). The result is given in Table 4.
The variable 1/LM is highly significant and positive. The variable LM is not significant at the 5 percent level but has, as a best estimate, a positive value. The minimum average cost point appears to be at 83 lane miles, where the average cost is $11,537.
Again, we want to see what the sensitivity of the costs to the number of miles is. Again, we will increase the minimum number is by 50 percent to 125 lane miles and decrease it to 42 lane miles. The results are, respectively, $11,549 and $11,573. Those increases are, respectively, 0.11 percent and 0.33 percent. That is not a very large effect and, as above, indicates a rather shallow minimum point.
Next, we add dummy variables for the individual communities. The equation resulting is in Table 5.
The minimum average cost is achieved at 82 lane miles. That gives an average cost of $11,510 per lane mile. A municipality with 50 percent more miles would have average costs of $11,523 or 0.11 percent more while a municipality with 50 percent fewer miles would have costs of $11,548 or 0.32 percent more. Again, this appears to indicate a U-shaped average cost, but with a fairly shallow dip.
Just as with the translog estimations, we will next estimate a frontier equation for the quadratic model. The result of this estimation is Table 6.
While the equation is highly significant, the coefficient on lane miles is not so. It tends to indicate economies of scale, without giving much confidence in that.
I have also run frontier regressions with LM and 1/LM as the single independent variables. The results are as follows in Table 7.
In these two equations, both of the coefficients for the variables are positive. In the first, as LM increases, the average cost per lane mile also increases, thus indicating economies of scale. In the second, as LM increases, 1/LM decreases and the average cost per lane mile decreases, thus indicating diseconomies of scale. Between the two, there is first decreasing average costs and then increasing average costs. This result is not as strong as that in the translog equation, but it does appear that there may be a most efficient size.
However we look at it, there appear to be U-shaped average cost curves. However, while the effect is statistically significant, it is not a large effect. Thus, there are only minor scale effects shown.
8. Market Power Effects
The first step in analyzing the effects of market power is to define just what we mean by the phrase “market
Table 4. Quadratic estimation—OLS.
Adj. R-squared = 0.11683; F-Test = 1370.8, Prob. = 0.00.
Table 5. Quadratic estimation—random effects.
Table 6. Quadratic estimation—frontier.
Table 7. Frontier estimation—linear forms.
power”. It is the extent to which the firm has price setting power and it depends on the numbers of competitors and their power. The standard measure of market power is the Herfindahl-Hirschman Index, or HHI, which is the sum of the individual firms’ squared market shares.
An important question in computing the HHI is the definition of the market. Here, it will be assumed that all of the highway providers in an area defined by the county compete with each other. Clearly, it also assumes that the providers do not collude with each other.
All of the highways in a county are owned by a) cities, towns, or villages, b) the county, or c) the state. Those owned by cities, towns or villages are within their boundaries and the jurisdictions do not generally overlap. County and state roads do, however, overlap with other jurisdictions. There is a method to the decision about who owns a highway in general. That is, the county may own a road that primarily facilitates travel among or between towns, cities, and villages even though it may also facilitate travel within communities. The state owned highways are meant to facilitate travel among or between counties even though it may also facilitate travel within counties.
A necessary question is how we should incorporate county and state roads when computing the HHI? Further, should we consider centerline miles or lane miles in the calculation? After all, county and state highways are more likely to be multiple lanes than are local roads but may have less/more traffic per lane. Perhaps county highways are more for commuting than are state highways. Certainly, some people have their houses located on county highways and thus use them for access just as local highways are used for access, the county highways will always be included. Since the appropriate market power is thus unclear, four measures will be tried. First will be based on center lines and include state highways, HHCS. The second will include state highways but be based on lane miles, HHLS. The third measure is based on centerlines and will not include state highways, HHCC. Finally, he fourth measure will be based on lane miles and will not include state highways, HHLC (The variable names are derived from Herfindahl Hirschman—HH, Center—C, Lane—L, S for State, and C for County only).
The area involved in each computation is the county. While some (9 in 2006) villages are partly located in more than one county, the actual miles in each county are computed in that county’s HHI. Thus, for example, the Village of Attica has 16 lane and 7 centerline miles in Genesee County and 1 lane and 1 centerline mile in Wyoming County in 2006. Note that the number of miles of each type of highway for each municipality also varies by year.
The correlations among the HHI measures are given in Table 8.
While it may seem that these are sufficiently close to each other that any one could arbitrarily be chosen, it is not particularly difficult to use all and let the reader choose.
The Federal Trade Commission has some rules, based on the HHI, that it applies to proposed mergers among firms in an industry20. Essentially, if the HHI is less than 1000, it will not challenge the merger, if the HHI is between 1000 and 1800, it will challenge the merger if the merger would increase the index by 100 or more, and if the HHI is more than 1800, it will challenge the merger if the merger would increase the index by 50 or more. The means of these indexes for the highways range from 1016 to 1087 while the individual indexes range from 402 to 2743. Thus, there are potentially a number of municipal mergers that, if they occurred in the private sector, would attract the attention of the FTC with the likelihood of opposition. Thus, many of the mergers advocated by those who argue for economies of scale would elicit opposition by the FTC, if it were to be involved, under its guidelines.
9. Translog Equations
We will use the same equations as before with the addition of the HHI variable. First, consider the use of LLM, LLM * LLM, and one of the HH indexes:
The OLS results are in Table 9.
The lowest cost mileages (efficient sizes) are, respectively, 199, 194, 207, and 210. Of more import is the fact that the coefficients on market power are significant well beyond the one percent level (two-tailed) and are positive. Thus, more market power does appear to result in an increase in average cost. Note that any extra expense due to this factor is simply waste from the taxpayers’ point of view21.
The average effects, which are multiplicative, are respectively 1.261, 1.308, 1.198, and 1.146. That is, at the average Herfindahl-Hirschman level for each measure, ranging from 1016 to 1086, the effect of that market power is to raise the average cost per lane mile by from 14.6 to 30.8 percent.
Table 8. Correlations among herfindahl/hirschman measures.
Adj. R-squared = 0.0738; F-Test = 511.11, Prob. = 0.
|
Variable |
coefficient |
standard error |
b/std. err. |
Sig. |
mean of x |
|
LLM |
−0.3524 |
1.37E−02 |
−25.803 |
0 |
3.9613 |
|
LLM * LLM |
0.0330 |
1.88E−03 |
17.54 |
0 |
17.058 |
|
HHCC |
1.69E−04 |
1.21E−05 |
13.98 |
0 |
1067.2 |
|
Const. |
9.7653 |
2.99E−02 |
326.43 |
0 |
Adj. R-squared = 0.0716; F-Test = 533.5, Prob. = 0.
|
Variable |
coefficient |
standard error |
b/std. err. |
Sig. |
mean of x |
|
LLM |
−0.3564 |
1.37E−02 |
−26.067 |
0 |
3.9613 |
|
LLM * LLM |
0.0333 |
1.89E−03 |
17.65 |
0 |
17.058 |
|
HHLC |
1.26E−04 |
1.15E−05 |
10.96 |
0 |
1086.7 |
|
Const. |
9.8204 |
2.96E−02 |
332.10 |
0 |
Adj. R-squared = 0.0683; F-Test = 506.69, Prob. = 0.
Let us calculate the sensitivity to a change in the HH level. First, suppose that the actual HH for a county is half the average for all counties. That would result in the average extra cost due to market power in that county’s municipalities being from 7.1 to 14.4 percent. That would be from 7.5 to 16.2 percent savings due to more competitive pressure. Second, suppose that the actual HH for a county is 50 percent more than the average for all counties. This would result in the average extra cost due to market power in that county’s municipalities being from 22.8 to 49.6 percent. That would be an increase from the average of from 8.1 to 18.8 percent. Again, that is pure waste to the taxpayers.
Now, we want to look at the case where, instead of OLS, we look at having dummy variables for each municipality (random effects model). The results follow in Table 10.
The optimal mileages are, respectively: 130, 139, 128, and 133. That is about 2/3 of the OLS results. For the market power results, they are not significant (at the 5 percent level) in 3 of 4 regressions although they tend toward the negative rather than positive. That suggests that much of the effect of the market power is actually municipality-specific.
Finally, let’s look at the frontier estimates. It could be argued that including the market power index in a frontier regression makes the assumption that market power is essentially a force of nature that forces inefficiency
Table 10. Translog estimation with HHI—random effects.
|
Variable |
coefficient |
standard error |
b/std. err. |
Sig. |
mean of x |
|
LLM |
−0.4903 |
4.16E−02 |
−11.797 |
0 |
3.9613 |
|
LLM * LLM |
5.05E−02 |
5.74E−03 |
8.793 |
0 |
17.058 |
|
HHCC |
−5.72E−06 |
3.91E−05 |
−0.146 |
0.88 |
1067.2 |
|
Constant |
10.198 |
9.33E−02 |
109.32 |
0 |
|
Variable |
coefficient |
standard error |
b/std. err. |
Sig. |
mean of x |
|
LLM |
−0.4924 |
4.16E−02 |
−11.832 |
0 |
3.9613 |
|
LLM * LLM |
5.04E−02 |
5.75E−03 |
8.751 |
0 |
17.058 |
|
HHLC |
−6.05E−05 |
3.61E−05 |
−1.674 |
0.09 |
1068.7 |
|
Constant |
10.268 |
9.17E−02 |
111.98 |
0 |
rather than a condition that allows inefficiency to occur. Of course, it could also be a result that can be expected due simply to human cupidity. By giving this result, the reader is given the choice of how it is to be interpreted. Accordingly, following are the frontier estimates in Table 11.
The most efficient number of lane miles for each of these is, respectively, 197, 191, 207, and 215. These efficient sizes are almost exactly the same as those for the OLS estimation.
Now for the costs at these frontier estimates. These are, respectively, $4560, $4536, $4568, and $4553. This compares with the average costs at the most efficient mileage for the OLS with dummy variables, respectively, of $8100, $8062, $8111, and $8088.
10. Quadratic Equations
First will be the OLS results with the various market power measures. These are given in Table 12.
The efficient numbers of lane miles are, respectively, 75.4, 72.7, 77.5, and 76.7. The average costs are, at these mileages, $11,535, $11,532, $11,536, and $11,535.
The next step, as with the translog estimation, is to estimate the quadratic functions with dummy variables for the individual communities. These results are given in Table 13.
The efficient numbers of lane miles are, respectively, 76.6, 76.2, 77.6, and 77.1. The average costs are, at these mileages, $11,510, $11,509, $11,511, and $11,510.
Table 11. Translog estimation with HHI—frontier.
|
Variable |
coefficient |
standard error |
b/std. err. |
Sig. |
mean of x |
|
LLM |
−0.3283 |
1.25E−02 |
−26.366 |
0 |
3.9613 |
|
LLM * LLM |
3.08E−02 |
1.81E−03 |
17.02 |
0 |
17.058 |
|
HHCC |
1.90E−04 |
1.22E−05 |
15.52 |
0 |
1067.2 |
|
Constant |
9.1001 |
3.04E−02 |
299.61 |
0 |
|
Variable |
coefficient |
standard error |
b/std. err. |
Sig. |
mean of x |
|
LLM |
−0.3314 |
1.24E−02 |
−26.695 |
0 |
3.9613 |
|
LLM * LLM |
3.09E−02 |
1.80E−03 |
17.16 |
0 |
17.058 |
|
HHLC |
1.48E−04 |
1.20E−05 |
12.38 |
0 |
1086.7 |
|
Constant |
9.1519 |
3.04E−02 |
300.49 |
0 |
Now for the frontier regressions. These results are given in Table 14.
The efficient numbers of miles estimated are, respectively, 31.6, 30.4, 39.1, and 38.9. These are about half of the efficient mileages estimated in the OLS and OLS with dummy variables (The low figures for the constant terms are due to the positive effect of the HH Index and are not particularly meaningful in their own right).
11. Implications
It would generally appear from the foregoing results that there are U-shaped average cost curves, with the minimum average cost points around 215 lane miles for the translog without dummy variables, and 80 lane miles for the quadratic without the frontier estimate. Because of the various forms used and their varying results for this, we cannot be as confident about the minimum average cost point as we are about the fact of the U-shaped average cost curves. Further, the AC curve is so shallow that it doesn’t make a great deal of difference if the mileage in a communityis a substantial difference from the potential minimum.
The results for the HH Index are quite strong and clearly have implications for whether municipalities should be allowed to merge. The average number of municipalities in a county was, during this period, about 27. Let us suppose a (made-up) example of some county with 27 municipalities, averaging 93 lane miles each. (This is the average for our sample as well). Suppose that there is one community with 500 miles, 3 with 300 each, 2 with 200 each, one with 100, and 20 with 30 each. The HH Index for this county is then 1005. Now, suppose one of those with 300 miles merges with one with 200 miles. The result would be an HH Index of 1197, an increase of 192. Since this exceeds the FTC figure of a 100 increase for a market over 1000, it would be expected that the
Table 12. Quadratic estimation with HHI—OLS.
Adj. R-squared = 0.1228; F-Test = 965.75, Prob. = 0.
Adj. R-squared = 0.1215; F-Test = 955.65, Prob. = 0.
|
Variable |
coefficient |
standard error |
b/std. err. |
Sig. |
mean of x |
|
LM |
1.0076 |
0.4847 |
2.079 |
0.038 |
93.358 |
|
LM1 |
6056.6 |
115.76 |
52.32 |
0 |
6.78E−02 |
|
HHCC |
2.4302 |
0.2014 |
12.07 |
0 |
1067.2 |
|
Constant |
8786.7 |
234.36 |
37.49 |
0 |
Adj. R-squared = 0.1230; F-Test = 968.8, Prob. = 0.
|
Variable |
coefficient |
standard error |
b/std. err. |
Sig. |
mean of x |
|
LM |
1.0332 |
0.4857 |
2.127 |
0.033 |
93.358 |
|
LM1 |
6070.1 |
115.93 |
52.36 |
0 |
6.78E−02 |
|
HHLC |
1.7147 |
0.1924 |
8.91 |
0 |
1086.7 |
|
Constant |
9541.4 |
228.73 |
41.72 |
0 |
Adj. R-squared = 0.1201; F-Test = 943.19, Prob. = 0.
merger would be opposed. Of course, the FTC does not generally deal in monopoly power for governments, so it would not get involved.
But, let’s look at the likely effect on the average costs. Based on the OLS translog equation with HHLC, the average cost, if it had previously equaled the average of the sample of $11,885, would rise by $291 to $12,176. It is important to note that this does not just apply to the communities involved but to all the communities in the affected county. Since there were assumed to be 27 communities with a total of 2500 miles, the result would be an increase in costs of $727,570 spread over the communities. Next, we’ll look at four different consolidation possibilities using actual communities and see what might occur. Of course, this is not to indicate any actual proposals for such consolidations.
In Cayuga County, NY, the HH Index (using local and county roads and lane miles, in 2006 was 1682. This is over the threshold where the FTC would question any change that would increase the Index by more than 100. Suppose that Sterling Town dissolved and Cayuga County took over their roads as well as those it already has. The result would be a new HH Index of 1953, or an increase of 271. The result, again using averages, would be an increase of 3.5 percent or $413/mile. That would add up to $1,084,926 for all the communities in Cayuga County. Of course, this would persist year after year.
Table 13. Quadratic estimation with HHI—random errors.
|
Variable |
coefficient |
standard error |
b/std. err. |
Sig. |
mean of x |
|
LM |
1.0183 |
1.3675 |
0.745 |
0.457 |
93.358 |
|
LM1 |
6134.1 |
329.43 |
18.62 |
0 |
6.78E−02 |
|
HHCC |
1.6688 |
0.5654 |
2.952 |
0.003 |
1067.2 |
|
Constant |
9571.9 |
658.90 |
14.53 |
0 |
|
Variable |
coefficient |
standard error |
b/std. err. |
Sig. |
mean of x |
|
LM |
1.0343 |
1.3720 |
0.754 |
0.451 |
93.358 |
|
LM1 |
6144.1 |
330.34 |
18.60 |
0 |
6.78E−02 |
|
HHLC |
1.1126 |
0.5333 |
2.086 |
0.037 |
1086.7 |
|
Constant |
10141.0 |
639.40 |
153.86 |
0 |
Another way in which a consolidation could occur would be a merger of a Town into a City. Suppose that, in Chemung County, NY, Elmira City were to take over Elmira Town. The HH Index in 2006 was 1100. The result, as Elmira City moved from 260 lane miles to 350 miles, would be to increase the HH Index to 1214, an increase of 114. Using the same procedure as above, the expected increase in per mile costs would be 1.4 percent or $172. The total for all communities in the county would be $347,507 each year.
A third possible merger would be the merger of two Towns. Take Schenectady County for instance and suppose that Glenville Town merged with Niskayuna Town (These are adjoining Towns and, of course, we are only considering merging the highway departments). The HH Index in 2006 was 1959. The merger would result in a new HH Index of 2203, an increase of 244. The expected increase in per mile costs would be 3.1 percent or $371. Over the entire county, the extra annual cost would be $591,110.
Our fourth example will be in Greene County, NY. We will assume that Catskill Village dissolves and is taken over by the surrounding Catskill Town. This would move the HH Index from 1166 to 1200 (That is the only one of the examples that would not—in the private sector—induce the FTC to take action). The consequence would be an increase in the average cost of about $51 per mile for all the communities in Greene County. The total cost increase would be about $97,508 per year.
We have now given examples where a) a Town is taken over by the County, b) a Town is merged into a City, c) a Town merges with another Town, and d) a Village dissolves and is taken over by a Town. In each case, costs can be expected to rise, affecting the surrounding communities as well as those directly involved. These effects appear to be more substantial than the scale effects, although the existence of an optimum scale also appears to be indicated.
Table 14. Quadratic estimation with HHI—frontier.
|
Variable |
coefficient |
standard error |
b/std. err. |
Sig. |
mean of x |
|
LM |
2.5431 |
9.18E−02 |
27.7 |
0 |
93.358 |
|
LM1 |
3884.6 |
29.58 |
131.3 |
0 |
6.78E−02 |
|
HHCC |
1.1534 |
7.70E−02 |
2.952 |
0 |
1067.2 |
|
Constant |
589.14 |
94.07 |
6.26 |
0 |
|
Variable |
coefficient |
standard error |
b/std. err. |
Sig. |
mean of x |
|
LM |
2.5627 |
9.30E−02 |
27.57 |
0 |
93.358 |
|
LM1 |
3881.0 |
30.086 |
129.0 |
0 |
6.78E−02 |
|
HHLC |
1.0399 |
7.45E−02 |
13.966 |
0 |
1086.7 |
|
Constant |
675.85 |
91.57 |
7.38 |
0 |
12. Population and Lane Miles
Most of the time when municipal consolidations are considered, the arguments are based on population rather than on lane miles of road. It is, therefore, desirable to find the relationship between population and mileage. Even if the mileage is best related to the costs, the use of population will give a measure that has more universal appeal to the public. Therefore, let us test for such a relationship. Let POPT be the population in thousands. A linear function is:
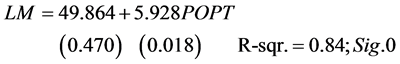
A random effects model with municipalities dummied out gives:
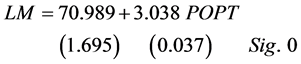
Both of these show a high correlation of Population with Lane Miles. They show that municipalities add 3 to 6 lane miles for each 1000 people added. The average population per municipality was 7337 and the average number of lane miles was 93.4 during the period studied. The average number of lane miles per 1000 population was 11.722.
Given the above, it would appear that, given the optimal number of lane miles in the translog OLS function of 232, the equivalent population figure would be about 30,200. If we use the random effects model above, along with the random effects translog model, the optimal number of lane miles would be 128 and the corresponding population figure would be about 18,800.
In any case, it would seem to be the case that mergers that increase the HHIndex by the FTC amounts and mergers that increase the lane miles to beyond about 230 or a combination there of, should not be undertaken. While the scale effect is only for the communities involved in the merger, the HHIndex effect harms the taxpayers in the whole market area even if they are not involved directly in the merger.
Acknowledgements
I very much appreciate the help of people at the NYS Dept. of Transportation for helping me obtain the data on highway mileages.
References
- Geys, B. (2006) Looking across Borders: A Test of Spatial Policy Interdependence Using Local Government Efficiency Ratings. Discussion Paper SP II 2006 - 03, Wissenschaftszentrum Berlin.
- Jiminez, B. and Hendrick, R. (2010) Is Government Consolidation the Answer? State and Local Government Review, 42, 258-270. http://dx.doi.org/10.1177/0160323X10386805
- Tiebout, C . (1956) A Pure Theory of Local Expenditures. Journal of Political Economy, 84, 416-424. http://dx.doi.org/10.1086/257839
- Southwick Jr., L. (2005) Economies of Scale and Market Power in Policing. Managerial and Decision Economics, 26, 461-473. http://dx.doi.org/10.1002/mde.1230
- Endreny, T.A. and Doherty, J. (2005) Snow Removal. In: The Encyclopedia of New York State, Syracuse University Press, 1428-1429,
- Grossman, P., Mavros, P. and Wassmer, R. (1996) Public Sector Inefficiency in Large US Cities. Working Paper, 96, California State University, Sacramento.
- Berg, W .D. (1972) Local Road Costs and Economies of Scale. Journal of the Transportation Engineering Division, 98, 881-890.
- Christofferson H. and Larsen, K.B. (2007) Economies of Scale in Danish Municipalities. Local Government Studies, 33, 77-95. http://dx.doi.org/10.1080/03003930601081283
- Goldin, K . (1968) Three Aspects of Highway Efficiency: Amount, Quality and Price. Journal of Transport Economics and Policy, 349-366.
- Bracknell Forest Council (2011) Highway Maintenance. 28 pages.
- Levinson, D . and Yerra, B. (2002) Highway Costs and Efficient Mix of State and Local Funds. Transportation Research Record 1812, Paper No. 02-2752, 27-36.
- Holcombe, R.G. and Williams, D.W. (2010) Urban Sprawl and Transportation Externalities. The Review of Regional Studies, 40, 257-273
- Holcombe, R .G. and Williams, D.W. (2012) Urban Sprawl and Transportation Externalities. The Review of Regional Studies, 40, 257-273.
- Charnes, A., Cooper, W. and Rhodes E. (1978) Measuring the Efficiency of Decision-Making Units. European Journal of Operational Research, 2, 429-444. http://dx.doi.org/10.1016/0377-2217(78)90138-8
- Amatatsu, H ., Ueda, T. and Amatatsu, Y (2011) Efficiency and Returns-To-Scale of Local Governments. Journal of the Operational Research Society, 63, 299-305. http://dx.doi.org/10.1057/jors.2011.38
- Afonso, A. and Fernandes, S. (2008) Assessing and Explaining the Relative Efficiency of Local Government. The Journal of Socio-Economics, 37, 1946-1979.http://dx.doi.org/10.1016/j.socec.2007.03.007
- Benito, B., Bastida, F. and García, J. (2010) Explaining Differences in Efficiency: An Application to Spanish Municipalities. Applied Economics, 42, 515 -528. http://dx.doi.org/10.1080/00036840701675560
- Brynes, J., Dollery, B. and Lopez, M. (2009) An Empirical Evaluation of the Relative Efficiency of Roads to Recovery Expenditure in New South Wales Local Government, 2005/06. Australasian Journal of Regional Studies 15, 311-328.
- Rouse, P. and Putterill, M. (2005) Local Government Amalgamation Policy: A Highway Maintenance Evaluation. Management Accounting Research, 16, 438-463. http://dx.doi.org/10.1016/j.mar.2005.07.003
- Rouse, P. and Putterill, M. (2003) Measuring the Effects of Local Government Reform: A New Zealand Highway Maintenance Application. Department of Accounting and Finance The University of Auckland, Auckland.
- Geys, B. and Moesen, W. (2009) Measuring Local Government Technical (In)Efficiency: An Application and Comparison of FDH, DEA, and Econometric Approaches. Public Performance & Management Review, 32, 499 -513. http://dx.doi.org/10.2753/PMR1530-9576320401
- De Palma, A ., Lindsey, R. and Quinet, E. (Eds.) (2011) A Handbook of Transport Economics. Edward Elgar Publishing, Cheltenham, 928 pp.
- Williams, D . (2006) The Impact of Population Density and Racial Composition on Municipal Government Expenditures. Dissertation, Florida State University, Tallahassee.
- Weicher, J. (1970) Determinants of Central City Expenditures: Some Overlooked Factors and Problems. National Tax Journal, 23, 379-396.
- Staley, S. (1992) Bigger Is Not Better: The Virtues of Decentralized Local Government. Cato Policy Analysis No. 166.
- Dollery, B., Brynes, J. and Crase, L. (2007) Is Bigger Better? Local Government Amalgamation and the South Australian Rising to the Challenge Inquiry. Economic Analysis & Policy, 37, 1-14.
- Faguet, J .P. (2000) Decentralization and Local Government Performance Improving Public Service in Bolivia. Revista de Economia del Rosario, 3, 127-176.
- Feiock, R. (2007) Rational Choice and Regional Governance. Journal of Urban Affairs, 29, 47 -63.
- Humplink, F. and Moini-Araghi, A. (1996) Is There an Optimal Structure for Decentralized Provision of Roads? The World Bank Policy Research Department Environment, Infrastructure, and Agriculture Division.
- Reingewertz, Y. (2012) Do Municipal Amalgamations Work? Evidence from Municipalities in Israel. Journal of Urban Economics, 72, 240-251.
- Staley, S., Faulk, D., Leland, S. and Schansberg, E. (2005) The Effects of City-County Consolidation: A Review of the Recent Academic Literature. Indiana Policy Review Foundation.
- Couch J., King, B., Gossett, C . and Parris, J. (2004) Economies of Scale and the Provision of Public Goods by Municipalities. Journal of Economics and Economic Education Research, 5, 69-79.
- Hicks, M. and Bohanon, C. (2008) Kernan-Shepard Commission and Local Government Expenditures Draft. Ball State University, Muncie, 13 pp.
- Geys, B., Heinemann, F. and Kalb, A. (2007) Local Governments in the Wake of Demographic Change: Efficiency and Economies of Scale in German Municipalities. Discussion Paper No. 07-036, Centre for European Economic Research.
- Link, H. (2006) An Econometric Analysis of Motorway Renewal Costs in Germany. Transportation Research Part A: Policy and Practice, 40, 19-34. http://dx.doi.org/10.1016/j.tra.2005.04.005
- Southwick Jr., L. (2012) Economies of Scale in Local Government: General Government Spending. iBusiness, 4, 265-278.
- Sjoqjuist, D. (1982) The Effect of the Number of Local Governments on Central City Expenditures. National Tax Journal, 35, 79-87.
- Lisk, D. (1998) Competing for Highway Maintenance: Lessons for Washington State. Policy Brief, Washington Policy Center.
- Federal Trade Commission (1992) 1992 Horizontal Merger Guidelines. http://www.ftc.gov/bc/docs/horizmer.htm
NOTES

1One can also consider that, as in Southwick for policing, there is more than one argument for consideration in the utility function. Inmovers may consider both cost and quality of the services in deciding on the place to move to or from. When I was in an elected position in Amherst, NY, I deliberately tried to create the appropriate service level and cost level to appeal to the upper mid-level income demographic categories.

2Because concrete lasts longer in general than asphalt, the municipality would generally prefer concrete. However, initial concrete costs are substantially more than asphalt. When the federal government builds parts of the interstate system, it pays 90 percent of the cost, leaving 10 percent for the state to pay. Then, it turns the highway over to the state, leaving the state to pay 100 percent of the maintenance. Since the state gets to choose the materials, naturally you will see the interstate highway system is, at least initially, entirely of concrete. State roads are more likely to be asphalt.
3If cracks are allowed to remain, dirt will collect and then plants will grow; their roots will tend to break up the pavement.
4Towns and Cities do not overlap and together consist of the whole land area of the State, at least in New York State. Villages are located within one or more Towns and, in some cases are coterminous with a Town.
5When I was a Councilman in Amherst (Town), NY, one road was owned in part (the southbound lane) by the Town and in part (the northbound lane) by the County. With the lawyers, I worked out an efficiency increasing swap so the Town owned both sides between two cross roads and the County owned both sides between two other cross roads.
6The county has some market power for this in that it has the power to turn over the ownership of the road to the Town within which it runs without the Town having much say in the matter.

7Of course, we have assumed, in effect, a continuous function which is not the case. However, the overall trend is what we are looking at here, so the result is appropriate for our needs.

8The author has been involved in negotiations that proceeded in precisely this fashion.
9Florida has warmer weather than New York generally so repairs can continue through the winter rather than having to be completed before it is too cold to work the materials. The author is familiar with one road improvement project in Florida where the work went on more or less continuously for five years. This is not usually done in New York; instead, a project is broken down into parts that can be completed within a year, before winter sets in.
10See, for more updated mileages (as well as for specific roads): http://www.search.its.ny.gov/search?q=road+miles+by+municipality&btnG=&client=dot_frontend&output=xml_no_dtd&proxystylesheet=dot_frontend&proxycustom=&sort=date%3AD%3AL%3Ad1&entqr=0&oe=UTF-8&ie=UTF-8&ud=1&site=dot_collection
11The data for each Town, Village, City, and for each year can be found on the Comptroller’s web site. See: http://www.osc.state.ny.us/localgov/datanstat/findata/index_choice.htm
12I telephoned a number of municipalities where there were ambiguities and asked who did their road maintenance. Where it was shared, the municipality where the ambiguity existed was deleted from the data set.

13In fact, New York State does require separate budgeting for snow removal and for the other functions. However, as a practical matter, transfers of monies can usually be made between these functions so that separation is not really accomplished. Where the taxpaying population is the same, it doesn’t matter, of course, in terms of tax rates where the funds are spent within the Highway Department.
14This is a difference from other states where the state government is not a wholly owned subsidiary of the unions.
15This was actually done a few years ago by a New York State Comptroller who was currying favor with the employee unions. (He was running for Governor at the time.) He gave this without any negotiations and without receiving anything in return for the taxpayers.
16Holcombe and DeEdgra also found that sprawl was not related to highway expenditures.

17See Charnes, Cooper & Rhodes, 1978 .

18The computer program is LIMDEP, v. 8.0, Econometric Software Inc., Plainview 2002, by W.H. Greene. 19Because the number of years is small relative to the number of municipalities, it would appear that the random effects assumptions are better than the fixed effects assumptions.

20FTC and .
21It may be viewed more favorably by the union members.

22Taking 5,280 feet per mile, 100 foot lots, and 3.25 people per house, the number of people per lane mile does seem to work out to be about the average, although the various municipalities are likely to differ greatly from this average.


