Received 22 October 2015; accepted 26 December 2015; published 30 December 2015

ABSTRACT

Growing water scarcity is one of the major challenges of the 21st century, especially in arid and semi-arid climates such as our study area. The efficient, sustainable and integrated groundwater management plays a key role for conserving this vital resource. In order to overcome this issue, the study of aquifer system’s behavior seems necessary. For this purpose, the areal piezometric level map is an essential tool. As piezometric level data are spatially limited in sample points, the spatial interpolation and geostatistics are the best way to produce the needed map. Several methods exist allowing to approach real values with varying degrees of accuracy. This work aims to compare and evaluate spatial interpolation methods for groundwater level of Haouz using a dataset of 39 piezometers. The deterministic methods used in this study are Inverse Distance Weighted (IDW) and Radial Basis Functions (RBF) and the probabilistic ones are ordinary kriging (OK), simple kriging (SK) and universal kriging (UK). This study shows the difficulty of having a key role to choose the suitable method for given input dataset. The best model remains the one that, after comparing several methods, offers the best accuracy, which is assessed using Cross-validation and statistical indicators. The results reveals that ordinary kriging with trend removal technique is the optimal method in this case. It indicates the superiority of this technique with a decrease in Root Mean Square Error (RMSE) up to 61.67%. It underestimates groundwater level with an average of 2.8%, which is reliable. The areal piezometric level and associated prediction standard error maps give additional information and recommendations that characterize the studied aquifer system and will ultimately improve sustainable groundwater management.

Keywords:

Geostatistics, Kriging, Piezometric Level, Groundwater, Haouz, Morocco

1. Introduction

Groundwater is a vital source of supply for urban and rural needs and socio-economic development across the world [1] -[3] . In the twenty-first century, the growing scarcity of useable water is in the midst of the most important challenges facing civilization [4] . Growing population causes more use and scarcity of water in various fields. Moreover, as an illustration to the extent of the phenomenon, the growth of crop production should reach 70% by the year 2050 more than it was in 2005 to feed the growing population [5] [6] . Furthermore, water scarcity in the world threatens all ecosystem components and has a direct impact on human life [7] -[9] .

All the threats stated above are exacerbated in arid and semi-arid climates. Amongst those climates, the Middle East and North Africa (MENA) region and particularly Morocco have to address water-related challenges even more than anywhere else. Besides, MENA region has been a focal area in discussions about the impact of water scarcity on food security [10] . Several international report and researches have revealed the alarming state of water in MENA region [11] -[16] . These reports and researches focus their recommendations, inter alia, on the importance of rational use of water and the crucial and pressing need of sustainable and integrated water management, especially for groundwater.

Understanding, analyzing and studying the behavior of aquifer systems is essential for making any management decision and for optimum exploitation and rational use of water [17] . The basic tool for this analysis is the regionalized map of piezometric level. It usually serves as a reference to the hydrogeological and environmental studies. It allows, among other, the understanding of the morphology, geometry and hydrodynamics of the aquifer [18] -[21] .

However, determining the groundwater level is usually accomplished during the in situ measurement campaigns. This makes the cost of data production substantial. Therefore data is spatially limited by a network of georeferenced points. This process can surely master the costs of the measures but it presents a major obstacle to the efficient study of the status of aquifer and the effects of hydrologic stresses on groundwater systems. In order to overcome these issues and reach the goals intended, the spatial interpolation for piezometric level is used to set up the regionalized map.

Spatial interpolation, mainly geostatistics, is the key tool to create this map. The research work carried out since the advent of this discipline is more than ever an essential capital [22] [23] . Researchers agree undeniably on the usefulness of geostatistics in the creation of spatially continuous data to make effective and confident decisions by managers and to make justified interpretations by scientists [17] [20] [24] -[27] .

Using geostatistics for processing groundwater data extends to several fields [25] [26] . It is adapted to be applied at each stage of hydrogeological modeling studies, from designing the data collection network to estimating the setting up of aquifers calibration models [20] . It was used to evaluate the groundwater storage [28] [29] . In addition, several researchers were interested in studying groundwater level evolutions and optimizing monitoring network using geostatistics [27] [30] -[33] .

In terms of interpolation, several methods exist allowing to approach real values with varying degrees of accuracy. In literature, every geostatistical method was created to respond to a particular situation of the given variable studied. However, some studies have shown the difficulty of providing a key role to select the optimal spatial interpolation method for a given dataset [26] [34] . The best model remains the one that, after comparing several methods, offers the best convergence ratio to the reality [26] [35] . In addition, the challenge in the spatial interpolation is the selection of optimum model that best represents the reality [34] .

Among the work carried out by researchers in the field of groundwater level interpolation, the authors Kumar [36] and Triki [37] compared some deterministic methods along with the probabilistic method universal kriging (UK). They used UK rather than other kriging types because of the presence of trend in their dataset. Their results revealed that kriging was more accurate than deterministic methods. While, the authors Sun et al. [35] conducted a comparison between deterministic methods Inverse Distance Weighted (IDW) and Radial Basis Functions (RBF) and the three types of kriging (ordinary kriging (OK), simple kriging (SK) and universal kriging (UK)). Their work has helped setting up a more precise ranking between the different methods in the following order: SK > IDW > RBF > OK > UK, SK being the most accurate and UK the less accurate.

In Morocco, Geostatistical approach has been used by many researches in different fields. For instance, the authors Jarar Oulidi et al. [38] used geostatistics to interpolate the transmissivity in the Cretaceous basin of Errachidia. It has also been used by Lahlou et al. [39] to study spatiotemporal variation of groundwater salinization in Tadla region. Finally, Rochdane et al. [40] used statistical and geostatistical methods to study the spatial variation of groundwater quality in the eastern part of Haouz.

Unfortunately, no comparison of spatial interpolation methods for groundwater level of Haouz has been made. Therefore, the objectives of this study are 1) to prove the inexistence of a key role for choosing the optimal method based only on input data distribution, 2) to compare the precision of probabilistic methods OK, SK and UK and the deterministic ones IDW and RBF on mapping the groundwater level in the study area. All comparisons between the models were assessed and carried out based on statistical accuracy indicators provided by cross-validation and statistics. The scope of this work directly affects the economic decision-making, policy and strategies for sustainable management of water. Indeed, the choice of the optimal method to interpolate the groundwater level in this region is a starting point for future studies to be conducted there.

2. Material and Method

2.1. Study Area and Data Used

The study area is located in the Haouz plain (Figure 1). It is limited by the High Atlas in the south and by Jbilet in the north. It extends from 8˚99 and 7˚28 degrees west longitude and 31˚16 and 31˚91 degrees north latitude. The groundwater flows in this area are established in the Pliocene-Quaternary alluvium and Neogene formations. They have a total capacity that varies between 50 and 80 m and can locally reach 120 m [41] . The climate is semi-arid, characterized by annual rainfall less than 300 mm with an annual evaporation of 2600 mm and annual temperatures between 15˚ and 30˚ [42] .

The groundwater of this area is overused [43] , given the drought that knows this area since the 70s and the

number of pumping stations continuously growing. The area is one of the oldest irrigated regions [44] .

The Hydraulic Basin Agency of Tensift manages the piezometric monitoring network in this area. It allows regular monitoring of the water level. This study involved a sample of 39 points measuring the groundwater level in May 2010. The positions of the piezometers are shown in Figure 1.

2.2. Methodology

In order to achieve the objectives set for the present work, a subdivision into three phases was needed. As shown in the Figure 2, this process consists of: 1) gathering and analyzing data, 2) comparing different interpolation methods, choosing the optimal final model and 3) regionalizing the variable studied by the best-chosen model.

The first step was to gather the data needed for this study and then integrate them into a spatial database to enable an easiest exploitation and analysis. Afterwards, data was analyzed and examined in different views within different mapping and statistical tools. This process helped to understand the distribution and spatial correlation of the variable. Also, it allows to detect abnormalities that can slide within the input dataset.

The next step was comparing and selecting the optimal model of each deterministic and probabilistic interpolation method: IDW, RBF, ordinary, simple and universal kriging. Then, these five optimal models were compared and the best one amongst all of them was selected and assessed. These methods are greatly described in the literature [45] -[48] . However, it is useful to recall the basis for the description of the methodology used in this paper.

All spatial interpolation methods, whether deterministic or probabilistic, can be represented as weighted averages of the measured data. They have the same general estimation formula as in Equation 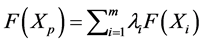(1):

(1)

where is the estimated value of a 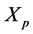point of the plane. 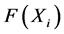is the measured value for each point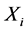. The weight assigned to each sampled point is represented by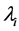. Finally, m is the number of sampled points

used in the estimation.

The major difference between all interpolation methods is mainly the way of calculating weight values (i.e.) of each point of the neighborhood. Probabilistic methods, unlike deterministic ones, take into account the degree of similarity observed in the calculation of weight values. For example, for the deterministic method like IDW the intensity of influence of the measured points is inversely proportional to the distance from the point to be calculated and points used.

While probabilistic methods family “Kriging” takes into account the spatial correlation between samples in the calculation of weight values. These correlations are studied from the semivariogram (also commonly known as variogram [49] ). It is a key tool in geostatistics. The kriging methods are labeled as a BLUE method (best linear unbiased estimator). In addition, it provides useful information on the uncertainty of interpolation.

To construct the experimental variogram, it is first necessary to calculate the semivariance. It can be defined as half the variance of the difference between pairs of samples for a distance h. It carries the following Equation (2) [48] :

(2)

where N(h) is the number of pairs separated by a distance h.

Once the experimental variogram built, it should be modeled. This is an important and crucial step in the interpolation process. This step consists on choosing the mathematical function (Spherical, Exponential, Gaussian, Bessel...) that best fits the experimental variogram. Here the parameters like sill, nugget effect and range should be changed until the optimum model is found.

To choose the optimal model and compare the interpolation methods, geostatistics uses Cross-validation, which is an essential tool. It also allows to validate and assess the accuracy of each method and model. It consists in predicting the value of each point in the data set by removing it and based on the remaining data. Thus, the difference between the measured and the estimated value can be calculated, from this follows several interpolation’s statistical accuracy indicators.

The quality assessment was carried out on the basis of three statistical indicators: Mean Error (ME) in Equation (3), Root Mean Square Error (RMSE) in Equation (4) and coefficient of determination R² in Equation (5). The validity of the model can be asserted when the mean error is close to zero, the RMSE is low and the R² is close to one.

Mean Error is the average of the difference between measured values and predicted ones:

(3)

Root Mean Square Error indicates how the model predicts the measured values:

(4)

Coefficient of determination R² is another statistical indicator for assessing the accuracy of the estimations. It measures the correlation between measured and predicted values. It is calculated as follows:

(5)

where P_ave is the average of the estimated value; C_ave is the average of the measured value; and n is the number of points used for estimation.

3. Results and Discussion

3.1. Exploratory Analysis

Exploratory analysis is an important step that allows to identify and to verify abnormal samples that could cause distortion in the calculation of the estimations. It also leads to an interpolation that can be the most representative of reality.

The analysis of the parameters Pearson kurtosis and skewness provides information on the distribution of the variable studied. Kurtosis Pearson (=3.9) being greater than 3, demonstrates a leptokurtic distribution type, which is more pointed than the normal distribution. The skewness (=0.82) being greater than 0 indicates an asymmetry in the distribution of data. The median (=469.06) and the average (=470.62) are significantly similar. This shows that the data is approximate to a normal distribution.

The sample map (Figure 1) is among the vital tools of exploratory analysis. It provides information on groundwater level’s distribution with proportional symbols. It reveals the variable’s spatial correlation. Moreover, it allows exposing the existence of trends. Furthermore, Figure 1 shows that the variable has a certain spatial continuity (auto-correlation), which means that spatial interpolation could be done. In addition, the low values are mostly in the northwest of the study area while strong values are in the southeast. This observation highlights the existence of a Northwest trend to decrease and Southeast trend to increase.

The same conclusion was provided by trend analysis tool (Figure 3). It uses a three-dimensional mark to represent the measured points. They are projected onto the XZ and YZ planes. When the projected line is flat we can conclude that no trend exists. In this case, Figure 3 shows the presence of a drift that can be modeled with a polynomial function. This trend is marked in the direction 115˚, which is approximately the main direction of groundwater flow in the study area.

In Figure 4, the experimental variogram was represented as a variographic surface. It helps to determine the isotropy or anisotropy [50] . The surface shows an isotropic model when the variability is the same in all directions. In this case, Figure 4 reveals anisotropic behavior with a wide variability in large distance in the direction 120˚, unlike perpendicular direction where variability is constant.

In addition, the Semivariogram Cloud tool (Figure 5) shows the empirical semivariogram values γ for all couples of locations plotted on the Y-axis against the distance h separating the two locations, which is plotted on the X-axis. This tool is used to examine the spatial autocorrelation of the phenomenon studied and detect abnormal values. Indeed, nearby locations (near zero on the distance axis) should be more alike (near zero on the semivariance axis). Therefore, high semivariogram values for sample locations within short distance may reveal that the data is inaccurate. The analysis of Figure 5 allows us to deduce that the input dataset is spatially correlated and does not contain abnormal values.

After this exploratory data analysis and prior to the interpolation of the groundwater level, we must compare, assess and choose the best model that can be the most accurate and representative of the study area.

3.2. Choice of the Optimal Method

Over 150 tests were conducted in order to find the optimal method for the given input dataset. In fact, for every method among all five we had to produce the optimal model: 1) Ordinary Kriging (OK), 2) Simple Kriging (SK), 3) Universal Kriging (UK), 4) Inverse Distance Weighted (IDW) and 5) Radial Basis Functions (RBF). Indeed, several parameters were tested in that matter. Then, the final five optimal models were compared and the best one was therefore selected. Cross-validation has been a key tool to select all the optimal models. The table below compares the optimal results for each method based on the indicators Root Mean Square Error (RMSE) and Coefficient of determination R²:

Furthermore, the Figure 6 shows a graphical representation of Table 1 to visualize the ranking of all the values of RMSE and the coefficient of determination R² of each optimal model of the five methods.

According to both the table and the Figure 6, ordinary kriging is the best representation of reality in this study area using the given input dataset, since it has the best accuracy indicators. Indeed, OK has the lowest RMSE and the highest R² coefficient (which is very close to 1). The ranking of the best interpolation methods from the more accurate (OK) to the less one (IDW) is: OK > SK > RBF > UK > IDW.

The results indicate the superiority of ordinary kriging technique with a decrease in RMSE up to 61.67%. In addition, OK is ranked better than UK technique, whereas our study variable is not stationary as it is mentioned in the exploratory analysis.

In literature, the OK method is designed specifically for stationary variables while UK method has been developed to interpolate non-stationary variables. However, the method called Trend Removal [50] [51] is

another way to predict this kind of variables. This method consists on isolating the drift and modeling it with a polynomial function (1st, 2nd or 3rd order), then the stationary part is kriged. Finally, and before the final calculation of the predictions is set up, the drift is added.

In our case, this Trend Removal method used in conjunction with OK was more accurate than modeling the non-stationary variable with UK method. As the piezometric level has a trend, it can therefore be subdivided into two sections and it is as follows: where d(s) is the first section responsible for the trend which is approximated by a polynomial function and the second section r(s) is stationary residue modeled by ordinary kriging.

This proves the inexistence of universal rule for choosing the optimal interpolation model. Comparing methods and assessing their accuracy using Cross-validation and statistical indicators are the best way. This finding follows the same conclusion of the authors Burrough et al. [34] , Li et al. [26] and Sun et al. [35] .

Assessing the accuracy of the best method chosen is based on the study of the correlation degree between the measured and the estimated values, which is conducted through Cross-validation and statistical indicators. Figure 7 shows the linear regression graph of measured and kriged values with the optimal model selected and the regression line. The calculated coefficient of determination R² = 0.986 demonstrates the existence of a strong correlation between the observed and the predicted values. Also, an F-test showed that this correlation is actually significant with confidence interval of 99% (α = 0.01). Therefore, we can deduce that this interpolation’s optimal method is accurate. Results showed that it underestimates groundwater level with an average of 2.8% which is reliable [30] . The chosen method is therefore applicable and accurate even for areas without measured data.

3.3. Prediction and Prediction Standard Error Maps

The result of this geostatistical study allowed to find the optimal interpolation method and to produce areal piezometric level map and the prediction standard error map.

Figure 8 shows the map of regionalized piezometric level estimated by ordinary kriging with trend removal technique. Its analysis demonstrates that groundwater flow occurs generally along the axis of the southeast area to the northwest. Indeed, the high values are found in the Southeast area and in the limit of the Atlas (830 m). While low values (300 m) converge towards the northwest of the study area in the nest of the Tensift River. In addition, this map provides information on the overall flow rate. It is important in the south and center compared to the Northwest region.

The spatial distribution of uncertainties is illustrated in Figure 9. This map demonstrates the reliability and the accuracy of predictions around the input dataset. Indeed, the uncertainty varies between 1 m and 4 m in the neighborhood of the measured point. While this error is around 13 m in far away observed values. Therefore, this map can serve as a basis to determine the optimal sites for new piezometers and to optimize the monitoring network. It shows the potential of this work, in the sense of increased accuracy of hydrogeological and environmental studies and reliability of decision making by economic and political actors.

4. Conclusions

Ordinary kriging with trend removal technique was chosen for its relevance and accuracy in describing the reality of the groundwater level of Haouz. It is the optimal method in the case of this study area and for the given input dataset. This result was reached after conducting a comparison between deterministic and probabilistic interpolation methods. Indeed, over 150 unit tests related to the parameters and mathematical models were needed to achieve this conclusion. In addition, cross-validation has played a decisive role in comparing and assessing the accuracy of every model.

This study also reveals and proves that there is no universal and key rule for choosing the optimal spatial interpolation model for a given dataset. Comparing methods and assessing their accuracy using Cross-validation and statistical indicators are the best way.

This optimal geostatistical method, in conjunction with mapping tools [38] [52] , has generated areal piezometric level map and the prediction standard error map associated with the kriged one. Analysis of these maps allows to detect the direction and speed of groundwater flow in the study area. These maps were also used to detect the optimal sites for new piezometers for the soul purpose of optimizing the monitoring network by the Hydraulic Basin Agency of Tensift. This recommendation will ensure the achievement of specific hydrogeological and environmental studies and will ultimately improve sustainable groundwater management. In addition, these maps offer the user, and particularly hydrogeologist, additional information about the identification and the characterization of the studied aquifer system.

Cite this paper

LamiaaKhazaz,Hassane JararOulidi,Saida ElMoutaki,AbdessamadGhafiri, (2015) Comparing and Evaluating Probabilistic and Deterministic Spatial Interpolation Methods for Groundwater Level of Haouz in Morocco. Journal of Geographic Information System,07,631-642. doi: 10.4236/jgis.2015.76051

References