Journal of Geographic Information System
Vol. 4 No. 6 (2012) , Article ID: 26322 , 13 pages DOI:10.4236/jgis.2012.46059
Validation of CA-Markov for Simulation of Land Use and Cover Change in the Langat Basin, Malaysia
1Department of Land Management, Faculty of Agriculture, Universiti Putra Malaysia (UPM), Serdang, Malaysia
2Department of Agriculture Technology, Faculty of Agriculture, Universiti Putra Malaysia (UPM), Serdang, Malaysia
3Department of Forest Production, Faculty of Forestry, Universiti Putra Malaysia (UPM), Serdang, Malaysia
4Swiss Federal Institute of Aquatic Science and Technology (EAWAG), Ueberlandstrasse, Switzerland
Email: *siva@putra.upm.edu.my
Received August 21, 2012; revised September 23, 2012; accepted October 25, 2012
Keywords: Land Use and Cover Change; CA-Markov; Calibration; Validation
ABSTRACT
Validity of CA-Markov in land use and cover change simulation was investigated at the Langat Basin, Selangor, Malaysia. CA-Markov validation was performed using validation metrics, allocation disagreement, quantity disagreement, and figure of merit in a three-dimensional space. The figure of merit, quantity error, and allocation error for total landscape simulation using the 1990-1997 calibration data were 5.62%, 3.53%, and 6.13%, respectively. CA-Markov showed a poor performance for land use and cover change simulation due to uncertainties in the source data, the model, and future land use and cover change processes in the study area.
1. Introduction
Globally, land use change impacts biodiversity, water and radiation budgets, emission of green house gases, carbon cycling, and livelihoods. The study of Land Use and Cover Change (LUCC) and its dynamics is crucial for environmental management, especially with regard to sustainable agriculture and forestry. Different models, in terms of structure and application, have been used to understand LUCC dynamics [1,2].
As emphasized by Verburg et al. (2004) [3], Chen and Pontius (2006) [4], and Luo et al. (2010) [5], LUCC models are fundamentally different, and have their own capabilities and limitations. Therefore, performance comparison of LUCC models is very difficult.
In this study, CA-Markov was chosen to simulate land use change based on the following requirements: dynamic simulation capability, high efficiency with data scarcity, simple calibration, ability to simulate multiple land covers and complex patterns.
CA-Markov has the ability to simulate land use changes among multiple categories and combines the CA1 and Markov chain procedures [6]. Markov analysis does not account for the causes of land use change and it is insensitive to space. However, CA-Markov using the CA approach relaxes strict assumptions associated with the Markov approach and explicitly considers both spatial and temporal changes [7]. CA-Markov also enables a more comprehensive simulation as compared to other LUCC models such as GEOMOD and CLUE [8]. However, CA-Markov calibration is operationally based on a single period of time, which renders difficulty in simulating land cover dynamics on a temporal scale [9]. In addition, the assumptions underlying CA-Markov method tend to be somewhat simplistic when looking at the micro-level changes in land use [10]. Pontius and Malanson (2005) [11] have demonstrated that the predictive power of CA-Markov is higher for cases where it concentrates on the major signal of land changes and ignores noises.
Pontius and Malanson (2005) [11] compared CAMarkov and GEOMOD in terms of simulation power and suitability for different applications in Central Massachusetts, USA. They applied a three stage method to measure simulation power. At first, calibration process was separated from validation process. Secondly, the accuracy was assessed at multiple resolutions. Finally, the calibrated model was compared to a null model that simulates pure persistence. Their investigation showed that the added complexity of spatial contiguity rule in CA-Markov was of no benefit. Paegelow and Camacho (2005) [9] studied the potential and limitation of prospective GIS2-based LUCC modeling. Their approach comprised the Markov chain for temporal simulationMCE3, MOLA4, and CA to perform spatial contiguity on the simulated land cover scores. Results showed three distinct limitations; the first was caused by complex variability within the land cover categories, the second was caused from using only two land cover maps for calibration, and the third was caused by the fact that MCE, MOLA, and CA only affected spatial distribution, and not temporal distribution, of simulated scores. In another study, Samat (2009) [12] applied CA-Markov to evaluate urban spatial growth in Seberang Perai, Malaysia. Validation analysis was performed using Kappa Agreement Index (KIA). In this work, the poor performance of CA-Markov in the development modeling of commercial/public facilities and industrial activities mainly resulted from: Model development based on physical factors, model assumption based on the uniform spatio-temporal growth of urbanized area, and inability of the model in recognizing new development. Samat et al. (2011) [13] showed that the prediction accuracy of CA-Markov decreased when the model tried to predict for a longer period of time, possibly due to the fact that a uniform transition rule was used by the model throughout the simulation period. According to Jokar Arsanjani et al. (2011) [14], the critical issue in employing CA-Markov is to combine the social, human and economic dynamics in the simulation, which can be realized in agent-based modeling systems. However, they tried to solve this problem using the integration of logistic regression and CA-Markov.
Araya and Cabral (2010) [15] modeled and analyzed urban land use change using CA-Markov and landscape metrics in Portugal. They reported that CA-Markov was validated successfully, with Klocation and Kquantity of 87% and 83%, respectively. However, they did not analyze the model capability for change simulation using a three-dimensional approach. Wang et al. (2010) [16] studied land use change based on vector data source using CA-Markov in China. Although the vector data improved simulation accuracy, validation analysis was performed only based on Kappa values.
Recent validation techniques proposed by Pontius and Millones (2011) [17] and Pontius et al. (2011) [18] allow the understanding of complex relationships caused by multiple simulation parameters. Additionally, these techniques facilitate three-dimensional spatial and temporal comparisons of LUCC, and eliminate the weakness of Kappa values for validation analysis.
This work was aimed at evaluating the capability of CA-Markov in simulating LUCC in a tropical catchment using the validation techniques proposed by Pontius and Millones (2011) [17] and Pontius et al. (2011) [18].
2. Materials and Methods
2.1. Study Area
In recent decades, the Langat Basin has undergone rapid urbanization, industrialization and agricultural development [19,20]. The Langat Basin is also a main source of drinking water for surrounding areas, a source of hydropower and plays an important role in flood mitigation. Over the past four decades, the Langat Basin has served approximately 50% of the Selangor State population. However, the Selangor State is currently facing water shortage problems, especially in urban areas [21-23]. Hydrometeorologically, the Langat basin is affected by two types of monsoon, i.e. the northeast (NovemberMarch) and the southwest (May-September) monsoons. Average annual rainfall is about 2400 mm. The wettest months are April and November with average monthly rainfall exceeding 250 mm, while the driest month is June with average monthly rainfall not exceeding 100 mm. Topographically, the Langat basin can be divided into three distinct areas with reference to the Langat River: the mountainous area in the upstream, undulating land in the centre and flat flood plain in the downstream (Figure 1). The basin has a rich diversity of landforms, surface features and land cover [23,24]. Dominant soil types in the basin are steepland and Rengam-Jerangau soil series with sandy clay loam and clay textures, respectively [20].
Due to the national importance of the Langat Basin, three sub basins (upstream of the Langat River), i.e. Lui, Hulu Langat, and Semenyih, with a total area of 694.13 km2 were selected for investigation of land use change (Figure 1).
2.2. Data Set
Land use maps dated 1990, 1997 and 2002 and soil maps, with the scale of 1:50,000 were collected from the Soil Resource Management and Conservation Division, Department of Agriculture, Malaysia. Ancillary data such as road and stream networks, contour lines, and population centers were extracted from the topographic maps, with the scale of 1:50,000. Landslide points, geology map (scale: 1/100,000), and location of the water treatment plants were obtained through the library of Universiti Putra Malaysia. Sawmill and oil refinery location maps were extracted from the agriculture yellow pages of Malaysia (www.yellowpages.com.my) and Google Earth. Daily TRMM5 radar data during 1998-2009 were obtained through the TOVAS and utilized to produce rainfall map. TRMM Online Visualization and Analysis System (TOVAS), developed by the NASA, provides a user friendly web-based interface for visualization and analysis of TRMM gridded rainfall products and other precipitation data [25]. In this work, land use classification

Figure 1. Geographic locations of the Lui, Hulu Langat and Semenyih sub basins within the State of Selangor, Peninsular Malaysia.
and map resolution (i.e. 30 m) were outlined based on the objective of a broad study, which was aimed at hydrological analysis of the Langat Basin during 1984-2020. The optimal pixel size was calculated based on the complexity of terrain method [26].
2.3. CA-Markov
A random process, X(t), is a Markov process if for any moment in time, t1 < t2 < ∙∙∙ < tn < tn + 1 [27]. The random process satisfies (see Equation (1) below) where: tn is the present time so that tn + 1 represents some points in the future and t1, t2, ∙∙∙ , tn − 1 represent various points in the past. Based on the present data, future is independent of the past. In other words, future of random process depends neither only on where it is now nor on how it got there [28].
If X[k] is a Markov chain with the states {x1, x2, x3, ∙∙∙}, then probability of transition from the state i to the state j in one time instant is,
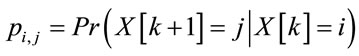 (2)
(2)
If Markov chain has a finite number of states, i.e. n, transition probability matrix can be defined as follows:
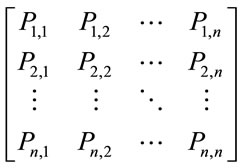 (3)
(3)
If transition probabilities vary with the time, the above matrix need to be written explicitly as a function of k (e.g. pi, j, k) [28].
CA-Markov in IDRISI program involves two techniques, i.e. Markov chain analysis and cellular automata [15]. Cellular automata underlie dynamics of the change events based on proximity concept so that the regions closer to existing areas of the same class are more probable to change to a different class. A cellular automaton is a cellular entity that independently varies its condition based on its previous state (according to a Markov transition rule) and adjacent neighbors [6]. The following 5 × 5 contiguity filter was utilized in this work:

2.4. Modeling
Firstly, three calibration periods, i.e. 1990-2002, 1997- 2002 and 1990-1997 were considered and correspondent simulation results were pre-analyzed in terms of goodness of fit. Results showed that the period 1990-1997 was more capable to simulate the future changes of land. Therefore, in this study, calibration data over the period 1990-1997 was used to extract transition probability matrix. Then two types of criteria (constraints and factors) were developed to determine which lands are suitable for future development. The constraint factors (dam reservoir and stream) were standardized into a Boolean value (0 and 1), while the parameter maps were standardized into a suitability continuous scale from 0 (minimum suitability) to 255 (maximum suitability) (Figures 2 and 3). Three types of fuzzy membership functions, i.e. sigmoidal, symmetrical, and user defined were used to rescale parameter maps into the range 0 - 255.
Analytic Hierarchy Process (AHP) was used to determine the weights of driving factors. AHP is a measurement theory founded on expert judgment to drive priority scales using pair wise comparisons [29]. In this method, comparisons are made based on a scale of absolute judgment that shows how much more one element prevails over the other for a given attribute (Table 1). However, the judgment may be inconsistent [30]. Considering n elements to be compared (C1 ∙∙∙ Cn), aij denotes the relative weight or priority of Ci over Cj. A = (aij) is a square matrix of order n with the constraints,  , for i ≠ j, and aii = 1. Such a matrix is considered as a reciprocal matrix. When the weights are transitive, they will be consistent and
, for i ≠ j, and aii = 1. Such a matrix is considered as a reciprocal matrix. When the weights are transitive, they will be consistent and  for all i, j and k. In this condition, Aω = λω, ω is an eigenvector (of order n) and λ is an eigenvalue. For a consistent matrix, λ = n. Human judgments are inconsistent to a greater or lesser degree, therefore in matrices concerning human judgment, the condition
for all i, j and k. In this condition, Aω = λω, ω is an eigenvector (of order n) and λ is an eigenvalue. For a consistent matrix, λ = n. Human judgments are inconsistent to a greater or lesser degree, therefore in matrices concerning human judgment, the condition 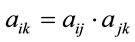 will not be reliable. In such a case, Aω = λmax × ω and λmax ≥ n. The difference between λmax and n is an indicator for inconsistency of the judgment. Consistency Index (CI) can be measured by
will not be reliable. In such a case, Aω = λmax × ω and λmax ≥ n. The difference between λmax and n is an indicator for inconsistency of the judgment. Consistency Index (CI) can be measured by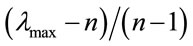 . Consistency Ratio (CR) is calculated as follows:
. Consistency Ratio (CR) is calculated as follows:
 (4)
(4)
where: RI is the Random Consistency Index which is a function of number of elements. If the CR exceeds 0.1, set of judgments may be too inconsistent to be reliable and the CR of zero means that the judgments are perfectly consistent [31].
SINMAP6 approach [32] under ArcView GIS was
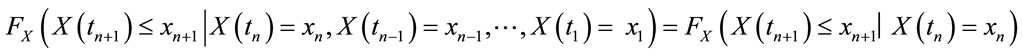 , (1)
, (1)
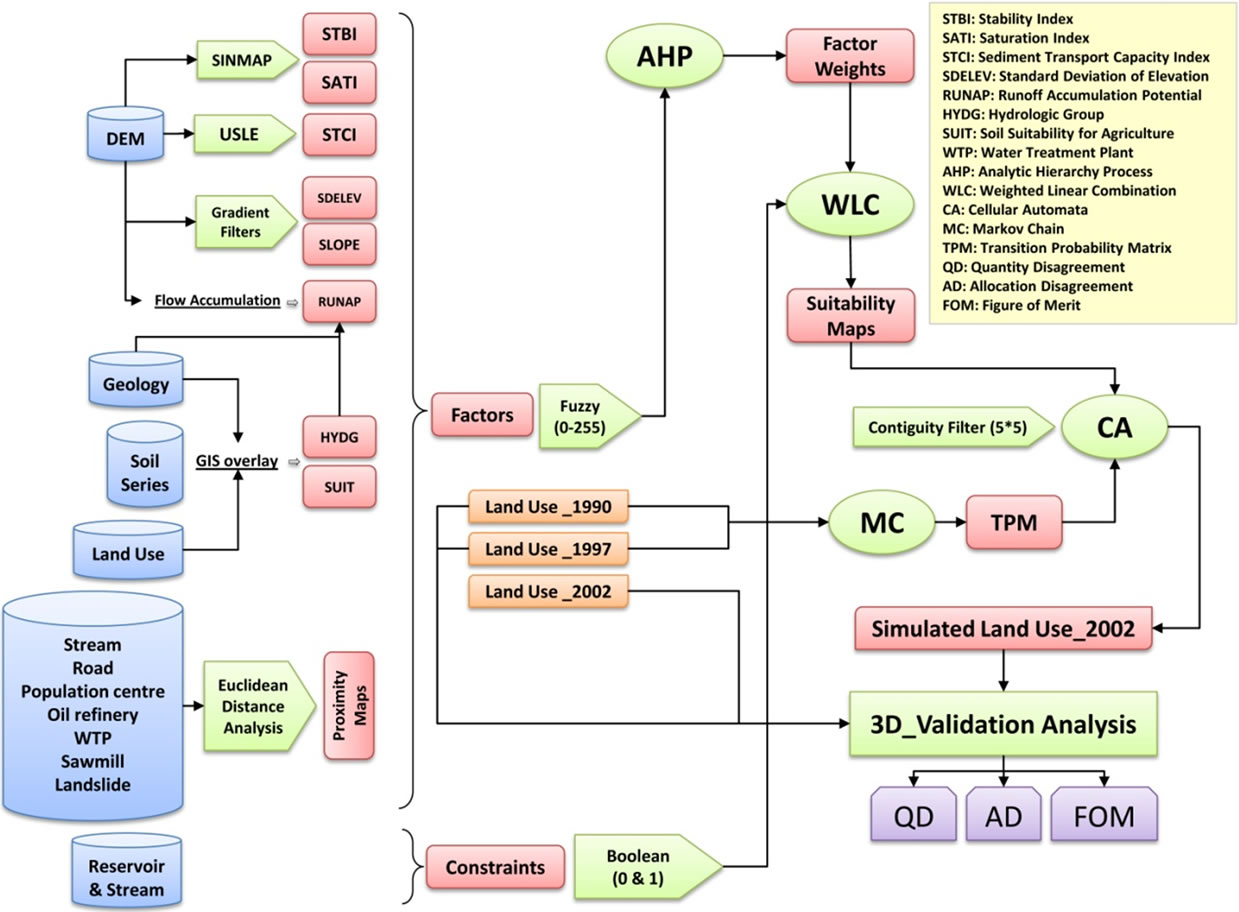
Figure 2. Computational framework of the study.

Figure 3. Transition suitability maps for different land covers generated using MCE.
applied to derive stability and saturation indices. Stability index was used in the extraction of suitability maps for agriculture, bare land, mining land, and urban areas, while saturation and roughness indices were used in suitability mapping for marshland and water bodies. Runoff accumulation map was produced based on impervious areas and Digital Elevation Model (DEM). This map was utilized to determine suitable areas for marshland and water bodies. Sediment transport capacity index (topography factor in USLE7 model) was used to extract suitability maps for grassland, marshland, and agriculture (Figure 2). Distance to sawmill and oil refinery centers were important parameters in the extraction of suitability maps for forest and oil palm stands, respectively. Distance to Water Treatment Plant (WTP) was used as a driving factor in AHP and MCE processes due to its impact on development of agriculture and urbanization (Figure 2).
As illustrated in Figure 2, Weighted Linear Combination (WLC) method was used in multi criteria evaluation of the drivers and constraints. WLC multiplies each standardized factor map by its factor weight and then sums the results. This result is then multiplied by each constraint to mask out unsuitable areas [6].
2.5. Model Validation
Land use map dated 2002 was used in the model validation, which was calibrated using the data of 1990-1997.
Disagreement parameters determine the disagreement between simulated map and observed map [17,18,33]. Quantification error (quantity disagreement) happens when the quantity of cells of a category in the simulated map is different from the quantity of cells of the same category in the reference map. Location error (allocation disagreement) occurs where location of a class in the simulated map is different from location of that class in the reference map [17]. These metrics were calculated based on the methods presented by Pontius and Millones (2011) [17] as follows.
2.5.1. Disagreement Components
These calculations and indices were derived directly from Table 2. J refers to the number of categories and number of strata in a typical stratified sampling design. Each category in the comparison map is indexed by i, which ranges from 1 to J. The number of pixels in each stratum is denoted by Ni. Each observation is recorded based on its category in the comparison map (i) and the reference map (j). The number of these observations is summed as the entry nij in row i and column j of the contingency matrix. Proportion of the study area (Pij) that is category i in the simulated map and category j in the observed map is estimated by the following equation [17]:

Table 1. Rating scale utilized in AHP (adopted from Saaty, 1980).

Table 2. Format of estimated population matrix (adopted from Pontius and Millones, 2011).
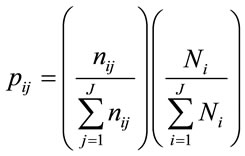 (5)
(5)
The Equation (6) calculates quantity disagreement (qg) for an arbitrary category g.
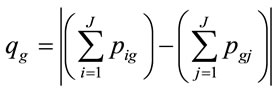 (6)
(6)
The overall quantity disagreement (Q) which incorporates all J categories is computed by Equation (7):
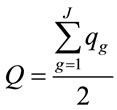 (7)
(7)
Allocation disagreement (ag) for an arbitrary category g is calculated using Equation (8). The first argument within minimum function is the omission of category g while the second argument is the commission of category g.
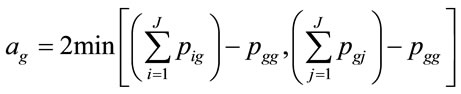 (8)
(8)
The overall allocation disagreement (A) is computed by the following equation:
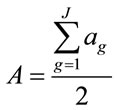 (9)
(9)
The proportion of agreement C is estimated by Equation (10):
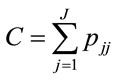 (10)
(10)
Based on Equation (11), total disagreement D is a sum of overall quantity of disagreement and overall allocation of disagreement:
 (11)
(11)
2.5.2. Figure of Merit
The figure of merit equals to the intersection of observed change and simulated change divided by the union of observed change and simulated change. The figure of merit ranges from 0, i.e. no overlap between real and predicted changes, to 100%, i.e. perfect overlap between real and predicted changes.
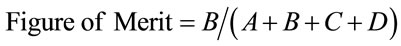 (12)
(12)
where: A is the area of error due to observed change simulated as persistence, B is the area of correct due to observed change simulated as change, C is the area of error due to observed change simulated as change to wrong category, and D is the area of error due to observed persistence simulated as change [33].
3. Results and Discussion
3.1. Land Use Change
Calibration of CA-Markov was done based on the changes in land cover over the period 1990-1997 (Figure 4).
According to transition probability matrix (Table 3), the biggest change occurred on grassland. Field and desk investigations demonstrated that grassland with bare land and mining land are transit categories and hence exposed to more changes during the time. Agriculture land8, oil palm and rubber stands also changed over the time. Agriculture land shifted mostly to oil palm and rubber plantings and urban areas while older rubber stands were transformed to agricultural and urban areas. Bare land changed mostly to grassland, forest and oil palm plantings. Forest stand primarily changed to grassland, mining land, urban areas, and rubber planting. Grassland and marshland mainly shifted to rubber planting, agricultural and urban areas. Mining land and oil palm stand changed
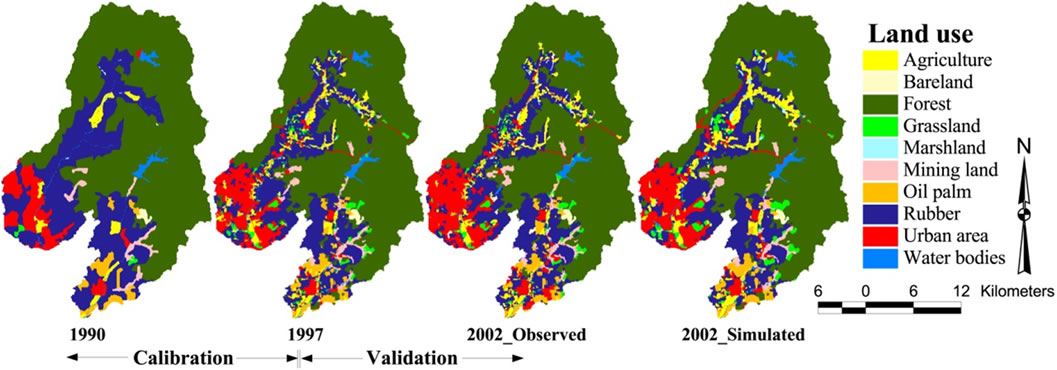
Figure 4. Observed land use map versus simulated land use map.
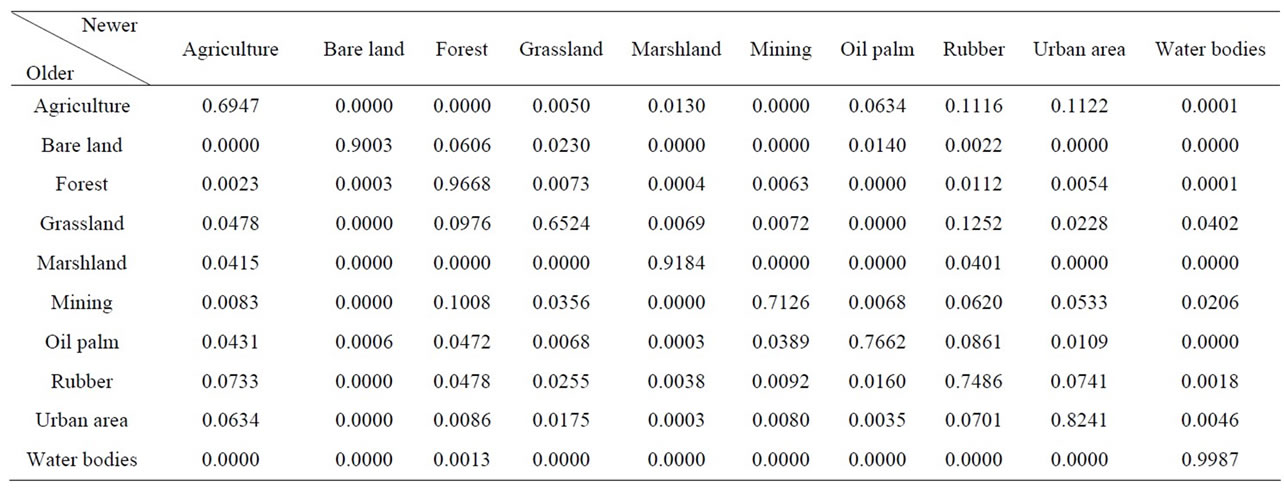
Table 3. Transition probability matrix for land use change modeling under the 1990-1997 calibration period.
primarily to forest and rubber plantings, bare land, and urban areas. In this region, water bodies did not change much. However, there were some transitions of water bodies to marshland and urban areas.
However, some of these changes in land use as indicated in the land use maps appear as a mismatch in reality. For example, the transitions of bare land and grassland to forest over a period of 7 years seem unreasonable. Also, the transition of urban areas to agricultural and rubber plantings seem unlikely under the Malaysian policy of land development at the time [34,35]. This mismatch is not caused by the model, but rather it could have been caused by the use of different land use classification criteria or inconsistent resolution of satellite imagery over the 12-year period.
As shown in Table 4, twenty factors were entered into AHP to determine the weights proportional to their importance in land allocation process. Consistency ratio in all land cover categories is lower than 0.1, which infers a consistent and reliable judgment. Figure 3 depicts the transition suitability of different land uses within the Langat Basin.
3.2. Validation
Based on error analysis (Tables 5 and 6), change simulation of bare land and grassland categories resulted in the lowest figure of merit, i.e. 47.39% and 49.45%, respectively. This could be due to the transit nature of these categories. Conversely, simulation of forest and water bodies resulted in the highest figure of merit, i.e. 94.39% and 80.32%, respectively. This could be caused by high percentage of persistence in these categories, i.e. 97% and 99% for forest and water bodies, respectively. Due to protection policy of the Hulu Langat Forest Reservoir, transition rate in the forest area was very low, which caused a high persistence. Figure of merit in change simulation of marshland and agriculture land was 51.03% and 57.42%, respectively. In simulation of agriculture land, quantity error was nearly similar to allocation error. This indicates that simulation of agriculture land is impacted by both types of errors. However, in simulation of marshland, quantity error was significantly higher than the allocation error. In this work, simulations of marshland and agriculture land were mostly impacted by transition inconsistency between calibration and validation periods. Figure of merit in change simulation of mining land and oil palm was 60.85% and 66.01%, respectively. In simulations of mining land and oil palm stands, transition consistency between calibration and validation periods was relatively high, which resulted in lower quantity error than allocation error. Figure of merit in change simulation of urban area and rubber stands was 76.37% and 67.71%, respectively. Change simulation of urban area was more affected by allocation error rather than quantity error. However, in simulation of rubber stands, due to transition inconsistency between calibration and validation periods, quantity error reached 2.39%.
Table 5 shows total quantity error, total allocation error, and total figure of merit calculated using a validation analysis over three time periods which are: reference T1, reference T2, and simulated T2. Using the same approach, components of agreement and disagreement as a fraction of landscape area are given in Table 6.
Total figure of merit, total allocation error, and total quantity error were 5.62%, 6.13%, and 3.53%, respectively. According to Table 6 and Figures 5 and 6, the components “persistence simulated as change” and “change simulated as persistence” were 5.63% and 3.46%, respectively. The model was able to correctly simulate only 0.57% of the changes. Simulated change is the sum of “persistence simulated as change”, “change simulated as change to wrong category” and “change simulated correctly.” Observed change is the sum of “change simulated as change to wrong category”, “change
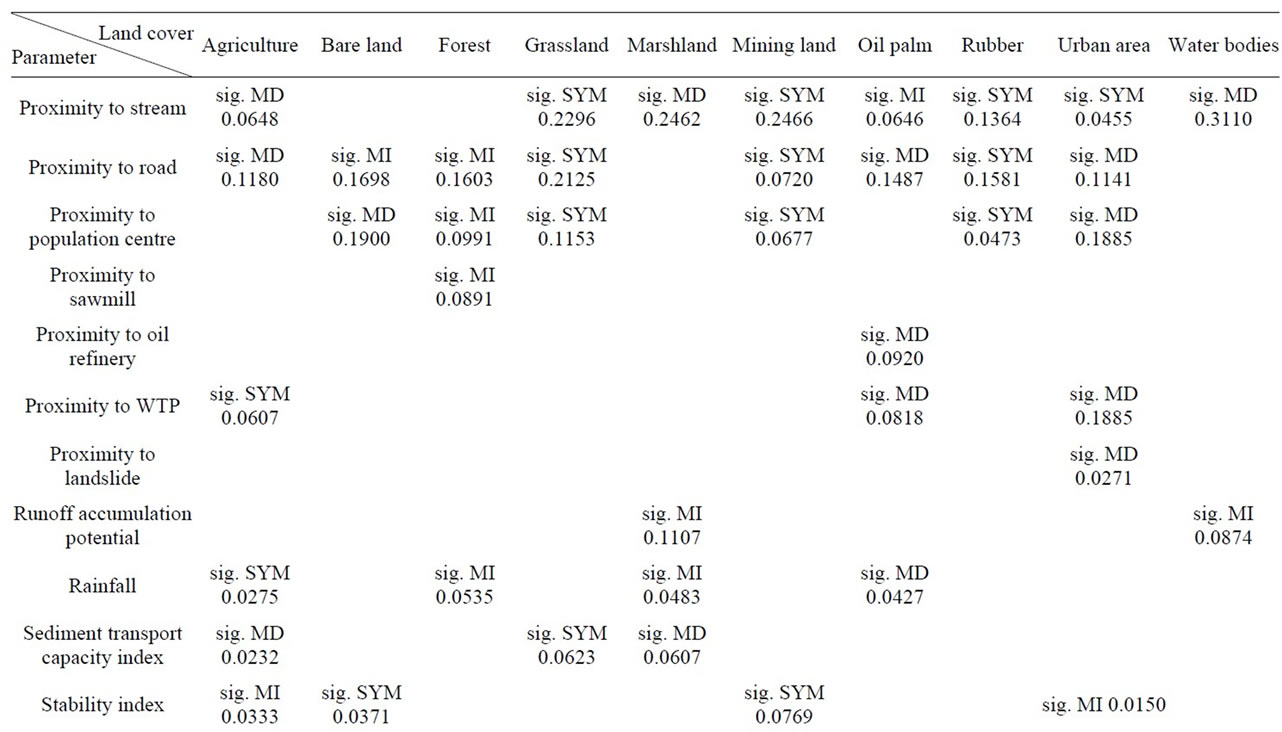

Table 4. Type of fuzzy membership function, eigenvectors of weight (values in italic) and AHP consistency ratio for each land use type.
simulated correctly” and “change simulated as persistence”. In this work, due to a high percentage of “persistence simulated as change”, simulated change (6.69%) was higher than the observed change (4.52%) (Table 6, Figures 5 and 6).
Validation results showed that CA-Markov did not accurately simulate land use change dynamics in the Langat Basin. The reasons are discussed in the following paragraphs.
As expressed by Pontius and Malanson (2005) [11], several LUCC models assume that land use change would be projected accurately using spatial dependency presented in a contiguity rule. However, Figure 4 shows that the new patches of bare land and grassland categories
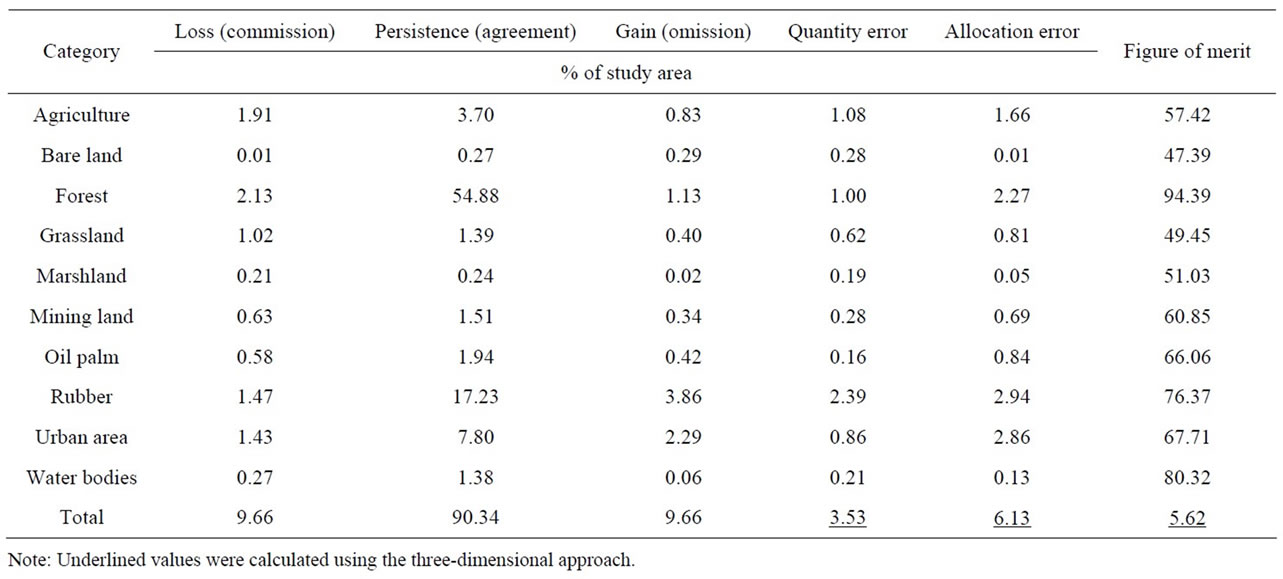
Table 5. Validation results for each category and total landscape.

Table 6. Validation results for simulations of total landscape using three-dimensional approach.
do not expand from existing patches. In the present study, CA-Markov imposes spatial dependency by the contiguity rule. As such, CA-Markov was unable to accurately simulate land use change for the bare land and grassland categories.
When the main signal of landscape is persistence, it is important that the model focus on the most important signal of change in the landscape. In this region, there were some noises resulting from the transitions of small patches specifically in agriculture and urban categories. These noises were projected by CA-Markov. However, studies have shown that the predictive power of CA-Markov is higher for cases where it focuses on major signal and ignores noises [11].
Land use maps utilized in this work were generated from satellite imagery, topographic maps, field surveys, and manual digitization. The digitized land use maps clearly showed some mismatch among the land use polygons, especially that of grassland, bare land and urban area, due to different interpretation of category definition. This led to some errors in the digitization process and consequently affected the simulation accuracy.
In this study, as confirmed by Pontius and Neeti (2010) [36], there were three sources of uncertainty, viz. the data, the model, and future land change processes. Calibration and validation processes in this study required land use maps in three points of time. The duration of time intervals was dependent on data availability. As mentioned previously, there were some inconsistencies between the calibration and validation periods in terms of change intensity that was mostly due to data scarcity and lack of freedom in data selection. This study also showed that CA-Markov was unable to simulate accurately based on marginal changes in land use over the given time period.
CA-Markov simulations using the 1990-1997 calibration data set had an overall Kappa of 89% and a standard Kappa of 85%. These Kappa agreement statistics infer high capability of the model in land use change simulation based on the given calibration period. However, the results of three-dimensional validation approach as proposed by Pontius et al. (2011) [18] demonstrated that these Kappa accuracies are mostly caused by high land persistence over time, as shown in this study (Figure 6 and Table 6). Therefore, the Kappa agreement statistics are unable to measure the strength of CA-Markov in simulating land use change. Typically, Kappa statistics compare accuracy to a randomness baseline. According to Pontius and Millones (2011) [17], however, randomness is not a logical option for mapping. In addition, several Kappa indices suffer from basic theoretical errors. Thus, it is recommended that quantity disagreement and allocation disagreement be used for accuracy assessment, instead of Kappa statistics.
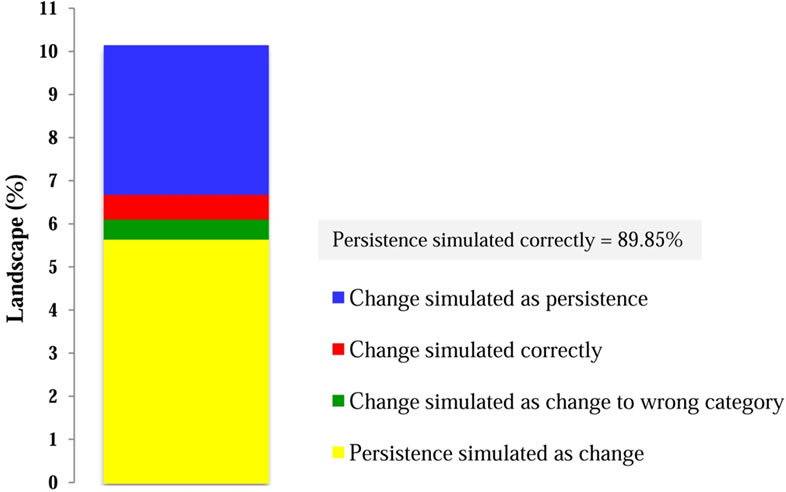
Figure 5. Components of agreement and disagreement.

Figure 6. Map representation of agreement and disagreement components.
Each LUCC model has its own capabilities and limitations. A single model is not capable to capture all of key processes in land use change projection [5]. In this study, the apparent differences in land use change between urban and non-urban areas were not well projected by CA-Markov. Therefore, according to the results of this study and other recent works [37,38], and with regard to data scarcity and the limitation of the applied resolution in this work, the following refinements are suggested as improvement to the simulation accuracy by CA-Markov:
1) Modeling urban and non-urban areas separately;
2) Integration of logistic regression and CA-Markov to prepare more realistic suitability maps;
3) Incorporation of more deterministic socio-economic parameters in land change simulation, such as population growth.
4. Conclusions
In this work, the validity of CA-Markov was studied using the 1990-1997 calibration period.
CA-Markov did not accurately simulate land use change dynamics in this area which resulted in the high values of quantity and allocation disagreements and low value of figure of merit computed using a three-dimensional approach.
Results showed that the new patches of grassland and bare land did not expand from existing patches. CAMarkov imposed spatial dependency by the contiguity rule, which caused inaccurate simulation of land use change for bare land and grassland. Moreover, CAMarkov simulation included noises which were dominant in agriculture and urban area categories. However, the projecting power of CA-Markov was higher in situations where major signals dominated over noises. Mismatching among land cover polygons due to different interpretations of land use definitions contributed to inaccuracies in the simulation of land use change. Data scarcity and lack of freedom in data selection caused some transition inconsistencies between calibration and validation intervals. In addition, CA-Markov exhibited difficulty in change simulation due to marginal changes in this area over time.
This study demonstrates the utility of three-dimensional analysis and disagreement components in validating land use change models.
5. Acknowledgements
The authors acknowledge Universiti Putra Malaysia for procuring the necessary data for this study.
REFERENCES
- P. H. Verburg, W. Soepboer, A. Veldkamp, R. Limpiada, V. Espaldon and S. S. Mastura, “Modeling the Spatial Dynamics of Regional Land Use: The CLUE-S Model,” Environmental Management, Vol. 30, No. 3, 2002, pp. 391-405. doi:10.1007/s00267-002-2630-x
- C. Kamusoko, M. Aniya, B. Adi and M. Manjoro, “Rural Sustainability under Threat in Zimbabwe—Simulation of Future Land Use/Cover Changes in the Bindura District Based on the Markov-Cellular Automata Model,” Applied Geography, Vol. 29, No. 3, 2009, pp. 435-447. doi:10.1016/j.apgeog.2008.10.002
- P. H. Verburg, P. P. Schot, M. J. Dijst and A. Veldkamp, “Land Use Change Modelling: Current Practice and Research Priorities,” GeoJournal, Vol. 61, No. 4, 2004, pp. 309-324. doi:10.1007/s10708-004-4946-y
- H. Chen and R. G. Pontius Jr., “GEOMOD Modeling,” Clark Lab, Clark University, Worcester, 2006.
- G. Luo, C. Yin, X. Chen, W. Xu and L. Lu, “Combining System Dynamic Model and CLUE-S Model to Improve Land Use Scenario Analyses at Regional Scale: A Case Study of Sangong Watershed in Xinjiang, China,” Ecological Complexity, Vol. 7, No. 2, 2010, pp. 198-207. doi:10.1016/j.ecocom.2010.02.001
- J. R. Eastman, “IDRISI Kilimanjaro, Guide to GIS and Image Processing,” Clark Lab, Clark University, Worcester, 2003.
- C. Agarwal, G. M. Green, J. M. Grove, T. P. Evans and C. M. Schweik, “A Review and Assessment of Land-Use Change Models: Dynamics of Space, Time, and Human Choice,” Northeastern Research Station, USDA Forest Service, Delaware, 2002.
- J. F. Mas, M. Paegelow, B. de Jong, O. Masera, G. Guerrero, M. Follador, et al., “Modelling Tropical Deforestation: A Comparison of Approaches,” 2008. www.csr.ufmg.br/dinamica/publications
- M. Paegelow and M. T. C. Olmedo, “Possibilities and Limits of Prospective GIS Land Cover Modelling—A Compared Case Study: Garrotxes (France) and Alta Alpujarra Granadina (Spain),” International Journal of Geographical Information Science, Vol. 19, No. 6, 2005, pp. 697-722. doi:10.1080/13658810500076443
- S. Srinivasan, “Land Use Change as a Tool: A Framework to Link Transportation and the Environment in New Delhi, India,” The Workshop on Transportation, Land Use and the Environment, Pune, 3-4 December 2001. http://www.deas.harvard.edu/TransportAsia/workshop_papers/Srinivasan.pdf
- R. G. Pontius Jr. and J. Malanson, “Comparison of the Structure and Accuracy of Two Land Change Models,” International Journal of Geographical Information Science, Vol. 19, No. 2, 2005, pp. 243-265. doi:10.1080/13658810410001713434
- N. Samat, “Integrating GIS and CA-Markov Model in Evaluating Urban Spatial Growth,” Malaysian Journal of Environmental Management, Vol. 10, No. 1, 2009, pp. 83-99.
- N. Samat, R. Hasni and Y. A. E. Elhadari, “Modelling Land Use Changes at the Peri-Urban Areas Using GEOGRAPHIC Information Systems and Cellular Automata Model,” Journal of Sustainable Development, Vol. 4, No. 6, 2011, pp. 72-84. doi:10.5539/jsd.v4n6p72
- J. J. Arsanjani, W. Kainz and M. Azadbakht, “Monitoring and Spatially Explicit Simulation of Land Use Dynamics: From Cellular Automata to Geosimulation—A Case Study of Tehran, Iran,” 2011 International Symposium on Image and Data Fusion (ISIDF), Tengchong, 9-11 August 2011, pp. 1-4. doi:10.1109/ISIDF.2011.6024203
- Y. H. Araya and P. Cabral, “Analysis and Modeling of Urban Land Cover Change in Setúbal and Sesimbra, Portugal,” Remote Sensing, Vol. 2, No. 6, 2010, pp. 1549- 1563. doi:10.3390/rs2061549
- L. Wang, H. Hu, X. Zheng, J. Deng and G. Ning, “Study on LUCC Based on Vector Date Source Using the CAMarkov Model,” 2010. www.ieee.org
- R. G. Pontius Jr. and M. Millones, “Death to Kappa: Birth of Quantity Disagreement and Allocation Disagreement for Accuracy Assessment,” International Journal of Remote Sensing, Vol. 32, No. 15, 2011, pp. 4407-4429. doi:10.1080/01431161.2011.552923
- R. G. Pontius Jr., S. Peethambaram and J. C. Castella, “Comparison of Three Maps at Multiple Resolutions: A Case Study of Land Change Simulation in Cho Don District, Vietnam,” Annals of the Association of American Geographers, Vol. 101, No. 1, 2011, pp. 45-62. doi:10.1080/00045608.2010.517742
- A. F. Mohamed, W. Z. Wan Yaacob, M. R. Taha and A. R. Samsudin, “Groundwater and Soil Vulnerability in the Langat Basin, Malaysia,” European Journal of Scientific Research, Vol. 27, No. 4, 2009, pp. 628-635.
- H. Memarian, S. K. Balasundram, J. Talib, C. B. Teh, A. M. Sood, K. C. Abbaspour and A. Haghizadeh, “Hydrologic Analysis of a Tropical Watershed Using KINEROS2,” Environment Asia, Vol. 5, No. 1, 2012, pp. 84-93.
- K. R. Ayub, L. S. Hin and H. Abd Aziz, “SWAT Application for Hydrologic and Water Quality Modeling for Suspended Sediments: A Case Study of Sungai Langat’s Catchment in Selangor,” International Conference on Water Resources (ICWR 2009), Langkawi, 26-27 May 2009. http://redac.eng.usm.my/html/publish/2009_09.pdf
- H. Juahir, S. M. Zain, M. K. Yusoff, T. I. Hanidza, A. S. Armi, M. E. Toriman, et al. “Spatial Water Quality Assessment of Langat River Basin (Malaysia) Using Environmetric Techniques,” Environmental Monitoring Assessment, Vol. 173, No. 1-4, 2010, pp. 625-641. doi:10.1007/s10661-010-1411-x
- H. Memarian, S. K. Balasundram, J. Talib, A. M. Sood and K. C. Abbaspour, “Trend Analysis of Water Discharge and Sediment Load during Past Three Decades of Development at the Langat Basin, Malaysia,” Hydrological Sciences Journal, Vol. 57, No. 6, 2012, pp. 1-16. doi:10.1080/02626667.2012.695073
- M. H. Noorazuan, et al. “GIS Application in Evaluating Land Use—Land Cover Change and Its Impact on Hydrological Regime in Langat River Basin, Malaysia,” Proceedings of the Conference Map Asia 2003, Kuala Lumpur, 2003. http://www.geospatialworld.net/index.php?option=com_c ontent&view=article&id=15467
- Z. Liu, D. Ostrenga, W. Teng and S. Kempler, “Tropical Rainfall Measuring Mission (TRMM) Precipitation Data and Services for Research and Application,” Bulletin of the American Meteorological Society, Vol. 93, No. 9, 2012, pp. 1317-1325. doi:10.1175/BAMS-D-11-00152.1
- T. Hengl, “Finding the Right Pixel Size,” Computers and Geosciences, Vol. 32, No. 9, 2006, pp. 1283-1298. doi:10.1016/j.cageo.2005.11.008
- A. A. Markov, “Extension of the Limit Theorems of Probability Theory to a Sum of Variables Connected in a Chain,” The Notes of the Imperial Academy of Sciences of St. Petersburg, VIII Series, Physio-Mathematical College XXII, 1907.
- S. L. Miller and D. Childers, “Markov Processes,” In: Probability and Random Processes, Academic Press, Burlington, 2004, pp. 323-367.
- T. L. Saaty, “The Analytic Hierarchy Process,” McGrawHill, New York, 1980.
- T. L. Saaty, “Decision Making with the Analytic Hierarchy Process,” International Journal of Services Sciences, Vol. 1, No. 1, 2008, pp. 83-98. doi:10.1504/IJSSCI.2008.017590
- G. Coyle, “The Analytic Hierarchy Process (AHP),” 2004. www.booksites.net
- R. T. Pack, D. G. Tarboton and C. N. Goodwin, “SINMAP, a Stability Index Approach to Terrain Stability Hazard Mapping,” UTAH State University, Logan, 2001.
- R. G. Pontius Jr., W. Boersma, J. C. Castella, K. Clarke, T. de Nijs, C. Dietzel, et al., “Comparing the Input, Output, and Validation Maps for Several Models of Land Change,” The Annals of Regional Science, Vol. 42, No. 1, 2008, pp. 11-37. doi:10.1007/s00168-007-0138-2
- R. Leete, “Malaysia, Achieving the Millennium Development Goals, Successes and Challenges,” The United Nations Country Team, Kuala Lumpur, 2005.
- I. Omar, “Rules Affecting the Land Development Process in Malaysia—A Review on Regulation of Environmental Impact Assessment (EIA),” 8th Pacific Rim Real Estate Society Conference, Lincoln University, Christchurch, 21- 23 January 2002, pp. 1-21.
- R. G. Pontius Jr. and N. Neeti, “Uncertainty in the Difference between Maps of Future Land Change Scenarios,” Sustainability Science, Vol. 5, No. 1, 2010, pp. 39-50. doi:10.1007/s11625-009-0095-z
- L. Poelmans and A. Van Rompaey, “Complexity and Performance of Urban Expansion Models,” Computers, Environment and Urban Systems, Vol. 34, No. 1, 2009, pp. 17-27. doi:10.1016/j.compenvurbsys.2009.06.001
- J. J. Arsanjani, M. Helbich, W. Kainz and A. D. Boloorani, “Integration of Logistic Regression, Markov Chain and Cellular Automata Models to Simulate Urban Expansion,” International Journal of Applied Earth Observation and Geoinformation, Vol. 24, 2012, pp. 265-275. doi:10.1016/j.jag.2011.12.014
NOTES
*Corresponding author.
1Cellular Automata.
2Geographic Information System.
3Multi Criteria Evaluation.
4Multi Objective Land Allocation.
5Tropical Rainfall Measuring Mission.
6Stability INdex MAPping.
/p>7Universal Soil Loss Equation.
8Refers to cultivation of annual field crops and horticultural crops, and does not include perennial industrial crops, i.e. oil palm and rubber.

