Journal of Mathematical Finance
Vol.2 No.3(2012), Article ID:22138,5 pages DOI:10.4236/jmf.2012.23029
The Simulation of European Call Options’ Sensitivity Based on Black-Scholes Option Formula
1College of Science, North China University of Technology, Beijing, China
2College of Economics and Business Administration, North China University of Technology, Beijing, China
Email: cyj@ncut.edu.cn, cyj8769@163.com
Received May 12, 2012; revised June 14, 2012; accepted June 23, 2012
Keywords: Black-Scholes Options; Sensitivity; European Call Options
ABSTRACT
As the Stock index futures with Cri 300 index for the subject matter launch, the research to stock options done by China’s financial market is gradually in-depth, which has great significance to the improvement of the financial markets. With the Black-Scholes option formula, this paper attempts to study the sensitivity of single stock’ call option named Industrial and Commercial Bank of China Limited to stock price changes, time changes and the situation that both of them occur. The simulation results were achieved based SAS, which not only has a very important practical significance to the launch of this kind financial derivative and the establish of a perfect pricing model of financial derivatives, but also can help financial market further promote economic growth.
1. Introduction
As a landmark, Black-Scholes option formula laid a series of financial derivatives, especially stock options [1,2]. With the fast developing of China’s financial industry, the research to financial derivatives is gradually in-depth, which has been proved by the launch of Stock index futures with Cri 300 index for the subject matter. With the Black-Scholes option formula, this paper attempts to analyze the changes of call option with single stock, ICBC [3], for the subject matter.
2. The Analysis of Black-Scholes Option Formula
The Black-Scholes option formula [2] is often described as following:
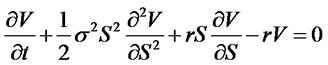
Then 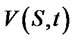 represents the present value of financial derivatives, which is based on the subject matter’s value
represents the present value of financial derivatives, which is based on the subject matter’s value ![]() and changes over time
and changes over time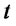 . Without considering the bonus and delivery of the block as subject matter, we can get European call options formula as following when the applicable conditions of Black-Scholes option formula are satisfied (derivation process referring to literature 4).
. Without considering the bonus and delivery of the block as subject matter, we can get European call options formula as following when the applicable conditions of Black-Scholes option formula are satisfied (derivation process referring to literature 4).
Then ![]() is the present value of call options and
is the present value of call options and 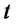 is present time.
is present time.
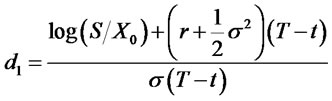

 is the exercise rice of subject matter stock to the maturity date
is the exercise rice of subject matter stock to the maturity date![]() .
.
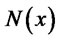 is standard normal distribution function.
is standard normal distribution function.
The approximate graphic of ![]() in the interval from –3 to +3 is shown as in Figure 1 [4].
in the interval from –3 to +3 is shown as in Figure 1 [4].
According to the definition of European call option, its value to the maturity date ![]() meet the condition:
meet the condition: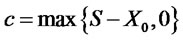 . Meanwhile it can’t be executed in advance, which is the great difference between European call option and American call option.
. Meanwhile it can’t be executed in advance, which is the great difference between European call option and American call option.
The pricing and risk research of European call option is more significant [5,6]. Meanwhile the development and application of financial derivatives and playing its innovation role in the modern financial markets have profound realistic significance.
3. Calculating the Related Parameters of Single Stock Option Approximatively According with Establishing Contions
Because the establishing conditions of stock options is
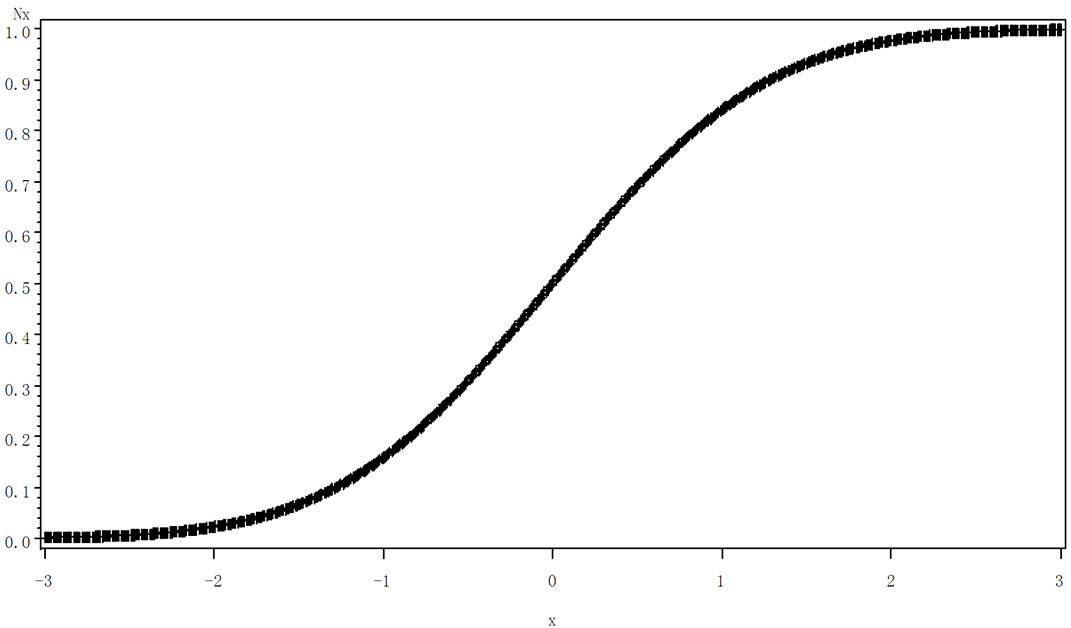
Figure 1. The figure of standard normal distribution function in the interval from –3 to +3.
strict, with the Black-Scholes option formula, we can only establish approximative option pricing model. This paper only analyze the pricing model of European call option due to the limit of paper length.
3.1. The Select of Subject Matter Stock for Call Options
According to the author’s statistical studies, the stock with small capitalization is difficult to meet the application conditions of Black-Scholes option because of its overlarge fluctuation. So we select ICBC, which has great capitalization, as the subject matter of single call option to establish approximative analysis model.
3.2. Collecting Related Data
Select each trading day’s closing price of ICBC during 1/1/2009 to 18/10/2011 as the subject matter stock’s approximative price![]() , which is selected in NetEase and will not be given particularly. Removing the date without trade, we can get 423 effective data.
, which is selected in NetEase and will not be given particularly. Removing the date without trade, we can get 423 effective data.
3.3. Calculating Option’s Related Parameters
Calculate sample average rate of return as approximation to replace drift rate and volatility in the option formula. Calculate the 423 data of ICBC With software SPSS 16.0, we get the result as following:
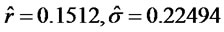
 selects 12 months as typical analysis stage.
selects 12 months as typical analysis stage.
It is selected as a typical analysis basis that the strike price of call option  is 10% higher than its recent average price. Of course we can choose other principles, which do not affect the results of analysis.
is 10% higher than its recent average price. Of course we can choose other principles, which do not affect the results of analysis.
4. The Related Simulation of Call Option
With Black-Scholes option pricing formula, we establish the model of ICBC by software SAS when we have calculated related parameters, and we can get relevant graphics describe.
4.1. The Affluence on Call Option Value Made by Asset Value Changing
From formula B-S we can get:
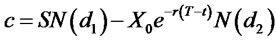 .
.
The explain of symbols and parameters refers to section I. Setting the closing price of ICBC in 18/10/2011 as a benchmark, strike price rises 10% that  (Yuan). Then we can get the changes of European call options’ value influenced by the price of the subject matter stock. We can get the expected graphic with software SAS as shown in Figure 2 in the condition that there is 12 months leaving to due data. From the Figure 2 we can get that there is a jump when the price is strike price, and jump range increased if the price is too far away from the present price. Vertical axis presents European call options’ price and horizontal axis presents stock price.
(Yuan). Then we can get the changes of European call options’ value influenced by the price of the subject matter stock. We can get the expected graphic with software SAS as shown in Figure 2 in the condition that there is 12 months leaving to due data. From the Figure 2 we can get that there is a jump when the price is strike price, and jump range increased if the price is too far away from the present price. Vertical axis presents European call options’ price and horizontal axis presents stock price.
4.2. The Sensitivity of Call Option to the Price of Subject Mattrr Stock
The relation between the change rate 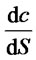 that option value compares with subject matter stock and stock price
that option value compares with subject matter stock and stock price
![]() is as following.
is as following.
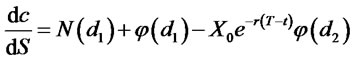
Then  is the function value when standard normal density function is at
is the function value when standard normal density function is at![]() . Data and parameters calculation accord to the result in III(A), then we get the simulation graph as shown in Figure 3.
. Data and parameters calculation accord to the result in III(A), then we get the simulation graph as shown in Figure 3.
From the figure we can get that there is intermittent
>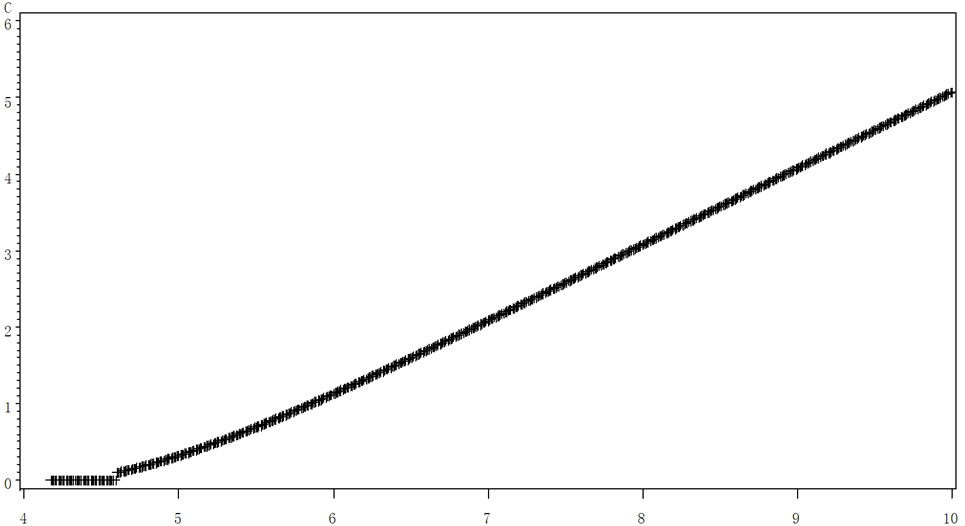
Figure 2. The function graph between call option and stock value.
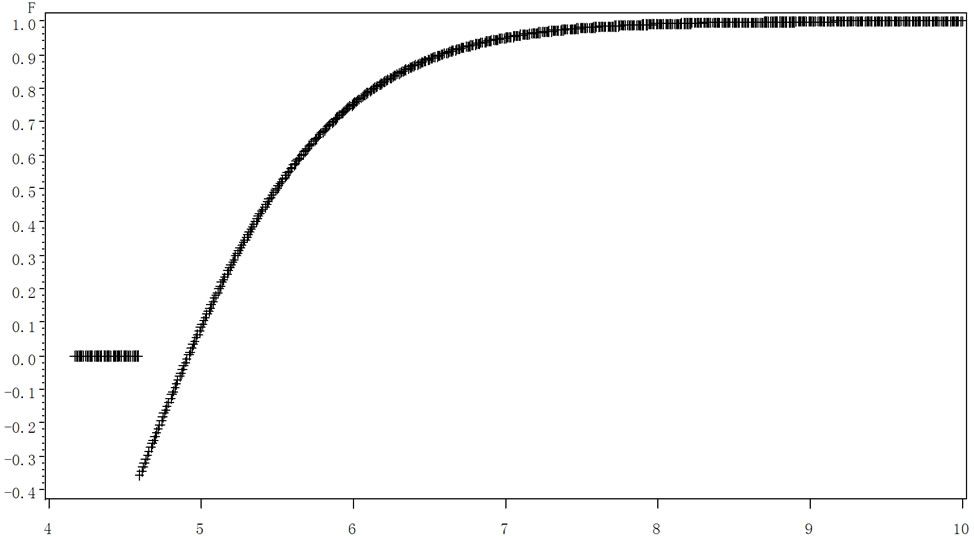
Figure 3. The graph describing the relation between the sensitivity of call option to the price of subject matter stock and stock price.
phenomenon when the price is strike price, which echo function’s changes. When the price of subject matter stock is far away from strike price, the change rate change rate that option value compares with stock value gradually becomes a constant value. That is to say call option’s price changes constantly comparing with the changes of subject matter stock.
4.3. The Sensitivity of Option’s Value to Time Change: Considering the Changes of Option Value under the Influence of the Time Function
Considering 12 months, the time consists of 252 days. Then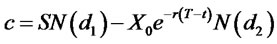 , we should pay attention that
, we should pay attention that 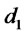 and
and 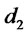 are still the function of time
are still the function of time . According to the result given in the previous sections, we can get all kinds of data and parameters. With software SAS, we can get the simulation graph of the relation among call option’s value, the price of subject matter stock and time function (as shown in Figure 4).
. According to the result given in the previous sections, we can get all kinds of data and parameters. With software SAS, we can get the simulation graph of the relation among call option’s value, the price of subject matter stock and time function (as shown in Figure 4).
5. The Analysis and Prospect of All Kinds of Risk
1) When the time is fixed, we have discussed the changes that option value compares with stock price in 4.2. 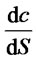 is rake ratio in the direction of subject matter stock when the time is fixed. Then the changes of option price can be given by
is rake ratio in the direction of subject matter stock when the time is fixed. Then the changes of option price can be given by 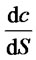 multiplying subject matter stock’s changes. If further considering the time changes and according to Taylor series expansion, we can get that:
multiplying subject matter stock’s changes. If further considering the time changes and according to Taylor series expansion, we can get that:
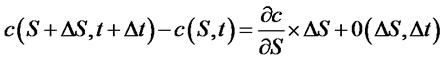
Here we can see that 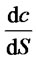 is still in the leading position.
is still in the leading position. 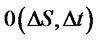 is a high order infinitesimal.
is a high order infinitesimal.
2) The second order partial derivative of option value to stock price is often called ![]() sensitivity, which is the change rate or sensitivity of
sensitivity, which is the change rate or sensitivity of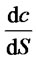 . When the volatility approved by market is not consistent with the one of subject matter stock,
. When the volatility approved by market is not consistent with the one of subject matter stock, ![]() sensitivity will play a great role, by analyzing which we can reduce model error.
sensitivity will play a great role, by analyzing which we can reduce model error.
3) We study the change relation among call option, the price of subject matter stock and due time in section IV(C). Of course we can further introduce the sensitivity of the time functions to make the research result more operational.
In a word, we can further study the relation among call option, the change rate of interest rate and the change rate of subject matter stock’s volatility, which has a very important practical significance to establish a perfect pricing model of financial derivatives and help financial
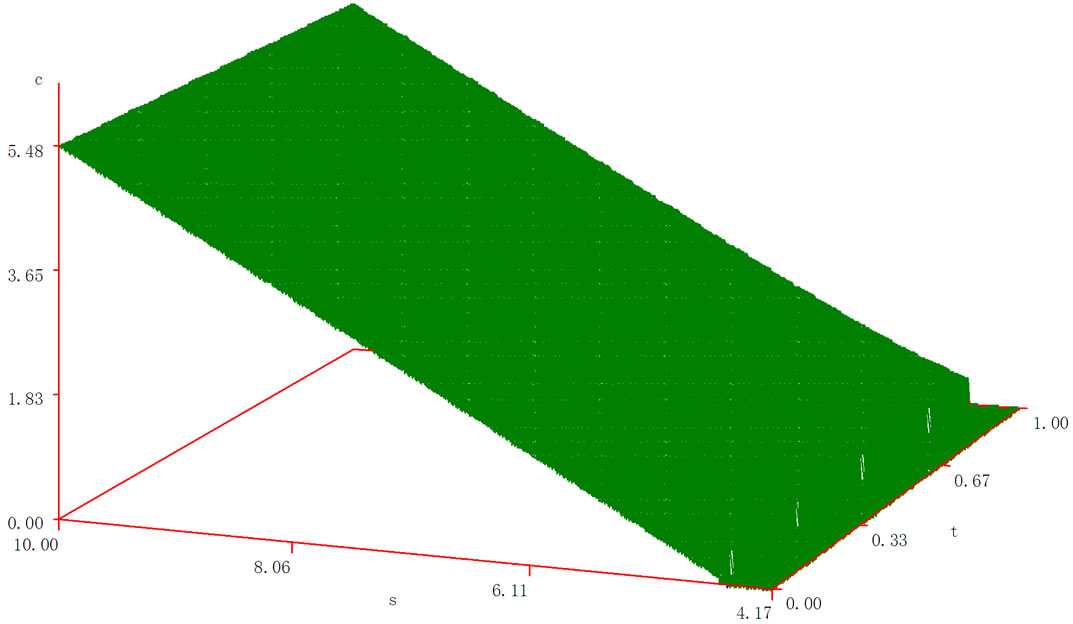
Figure 4. The relation among call option, the price of subject matter stock and due time.
market further promote economic growth.
6. Acknowledgements
The projects of Beijing municipal education commission: No. KM201010009011 & National Natural Science Foundation of China (11171002), Beijing Natural Science Foundation (the theory of mixed effects models of multivariate complex data and its applications; 1112008) & College Student Research and Career Creation Program of Beijing (2012).
REFERENCES
- F. Black and M. Scholes, “The Pricing of Options for Alternatives Stochastic Processes,” Journal of Political Economy, Vol. 81, No. 3, 1973, pp. 637-654. doi:10.1086/260062
- F. Black, M. Jensen and M. Scholes, “The Captial Asset Pricing Model: Some Empirical Tests,” Studies in the Theory of Capital Markets, Praeger, New York, 1972.
- http://quotes.money.163.com/0601398.html
- S. W. Zhu, “Financial Calculation and Modeling: Theory, the Algorithm and SAS Program,” Tsinghua University Press, Beijing, 2007.
- F. M. Song, “Financial Engineering Principle: No-Arbitrage Equilibrium Analysis,” Tsinghua University Press, Beijing, 1999.
- P. Wilmott, “Financial Engineering and Risk Management Techniques,” Mechanical Industry Press, Beijing, 2009.

