Natural Science
Vol.5 No.1(2013), Article ID:26616,3 pages DOI:10.4236/ns.2013.51007
Depth decay rate for surface gravity wave pressure and velocity
![]()
4632 North Lane, Del Mar, USA; Kernken@aol.com
Received 27 October 2012; revised 26 November 2012; accepted 10 December 2012
Keywords: Surface Gravity Waves; Depth Decay Rate
ABSTRACT
Linear governing equations are formulated for the depth decay of the pressure and velocity variations associated with propagating surface gravity waves. These governing equations come from combining Bernoulli’s equation for steady frictionless flow along a streamline and the crossstream force balance involving gravity, the centrifugal force and a pressure gradient. Qualitative solutions show that the pressure decreases downward faster than the velocity does and at a rate that is probably not the normal exponential decrease, which does not agree with the classical result. The radius of curvature of the streamlines is a non-constant coefficient in these equations and it needs to be supplied, either from measurements or another theory, in order to complete the solution of the derived governing equations. There is no sensitivity of the solution to the exact path the radius of curvature takes between its minimum value at the surface of a crest and trough and infinity at great depth. In the future measurements, perhaps streak photographs, will be needed to distinguish between the new and old theories.
1. INTRODUCTION
The finite depth of wave influence for the surface gravity wave has been recognized since the 1600s when, in a diving bell on the bottom of the English Channel, Edmond Halley described how he could work on salvaging sunken treasure undisturbed by the waves at the surface [1]. Now, submarines can ride out a storm at sea in comfort while submerged at a depth greater than or equal to about one typical wavelength.
A mathematical explanation of this phenomenon has been available since the 1800s in which both the pressure and the velocity variations decay exponentially with increasing depth away from the mean free surface and at the same decay rate, or e-folding scale that is proportional to the wavelength [2].
In 1942 there came a purely physical explanation due to Sverdrup [3]. Since the vertical acceleration of the fluid is downward at a crest and upward at a trough, pressure variations at a fixed depth due to the combined effects of the acceleration of gravity and of the vertical fluid acceleration, will vanish when the fixed depth is sufficiently large. Part of this explanation also involves the realization that a vertical column of water raised to the surface from the fixed depth of constant pressure is larger under a crest than under a trough, and by an amount equal to the wave height, in fact.
Sverdrup’s idea has a certain innate beauty because it can be contained in a nutshell and it is about as elementary as can be in this business. However, some sticking points are left out. For example, there is a presumption that at the depth where the wave pressure variations vanish, the velocity variations also vanish. It is not a priori obvious that this should be so. Also no guidance is provided for how to relate this “depth of wave influence” to any other wave property, such as the wavelength. In other words, the idea itself is very interesting, but it apparently needs to be combined with ancillary information in order to become more useful [4]. In addition, the rate of decay of the wave properties with increasing depth is not specified.
What is attempted below is to give a simple physical explanation for the depth decay rate for pressure and velocity variations. It is found, in contrast to the classical mathematical results, that the pressure and velocity variations decay at different rates, the pressure decaying faster than the velocity. And neither decay rate is the normal exponential one in all probability.
One well-known example has existed for a considerable time, probably starting with Newton, in the field of steady fluid flow whereby pressure and velocity do not decrease at the same rate: solid body rotation inside a rigid cylinder oriented vertically with gravity acting downward [5]. This is sometimes called the problem of the spinning bucket of water. Amazing is the controversy the spinning bucked problem has endured over the 300 years, which is related to the controversy surrounding the centrifugal force in the minds of most physicists. At any rate, the velocity decays linearly inward from the cylinder’s surface to its center whereas the pressure decays quadratically inward, as indicated by the parabolic shape of the air/water interface. Apparently this example did not generate any wider search within fluid dynamics for disparate decay rates for pressure and velocity in other steady flows.
However, Bernoulli’s equation has been there patiently waiting to point the way. In a single equation Bernoulli’s law combines terms the mathematician would designate as zeroth, first and second order. It would be a shame to destroy this wonderful equation by making a set of equations, each one of which contains only terms of the same order, but that is what the perturbation expansion technique is capable of doing.
2. CALCULATION
In order to approach answering the question of the decay rate of the wave properties with depth, two elementary pieces of physics are put together: Bernoulli’s equation for steady frictionless flow along a streamline and the balance between two equal but opposite forces on the curved flow below the crest of a wave, for example. Helpful for visualization here is the so called steady reference frame in which the wave form is fixed in position and the fluid flows past the observer under the crest and trough in a sinusoidal pattern.
As the fluid flows under the crest there is a upward centrifugal force acting on it due to the curvature of the fluid particle trajectory. The tendency of the centrifugal force is to tear water away from the top of the crest and fling it into the air. Since this is not observed to happen in most cases, the centrifugal force must be balanced by an equal but opposite force acting downward. Otherwise turbulence or chaos would result. In this situation the counter-balancing force has to be a pressure gradient plus the force of gravity. For small wave slopes gravity is the smaller of the two forces opposing the centrifugal force at the crest. However, no small slope assumption needs to be made in what follows. Just wave breaking must not take place in order to maintain steady motion.
Friction is neglected in what follows. Constant density, or incompressibility, is adopted for convenience. Far below the wave surface the velocity of the fluid is constant in magnitude, U, and direction, in accordance with observations. Normal to the mean flow and at the top of the crest the z-axis points up (the zero value is taken at the top of the crest).
Bernoulli’s equation for steady frictionless flow along a streamline is
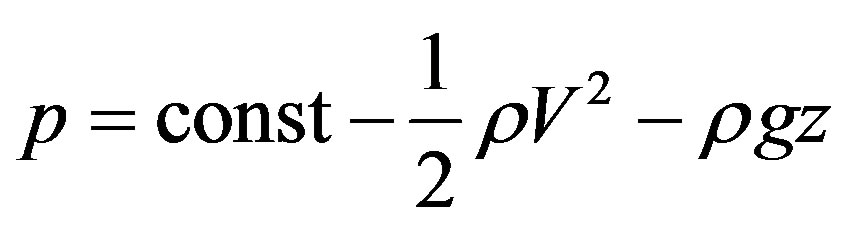 (1)
(1)
Where p is the pressure, V the speed of flow, ρ is the constant fluid density and g is the acceleration of gravity. For simplicity the constant in Eq.1 will be assumed to be the same for all streamlines.
The force balance at the top of the crest is
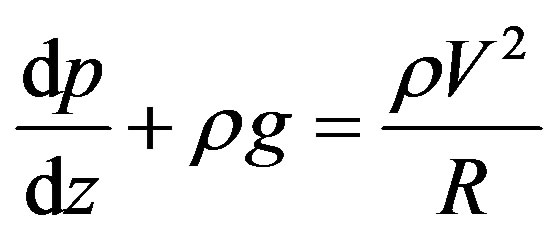 (2)
(2)
Where R is the radius of curvature of the streamlines at and below the crest, and it is a function of z.
Between Eq.1 and Eq.2 the pressure can be eliminated by first taking the z derivative of Eq.1 and then combining that with Eq.2, which produces
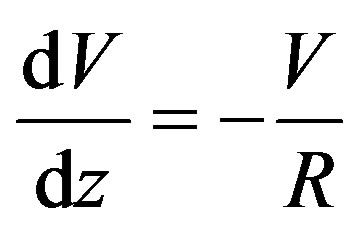 (3)
(3)
Unlike either equation it came from, Eq.3 is linear and therefore can be solved. It is also a first order ordinary differential equation. The only potential difficulty is that there is a non-constant coefficient, R (z), which information needs to be supplied before the solution of Eq.3 can be completed. Observations might be used to delineate the radius of curvature function, for example. In any case, linearity is such an advantage for an equation over the usual nonlinearity in surface gravity wave problems that it is a worthwhile starting point while a search is taking place for a way around the difficulty of the non-constant coefficient.
To see what can be learned without specifying the curvature function, separate variables in Eq.3 to get
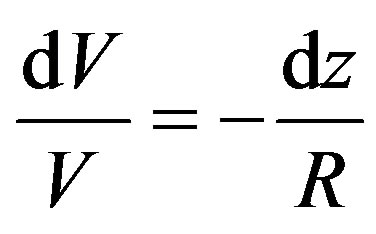 (4)
(4)
Then each side of Eq.4 can be integrated separately
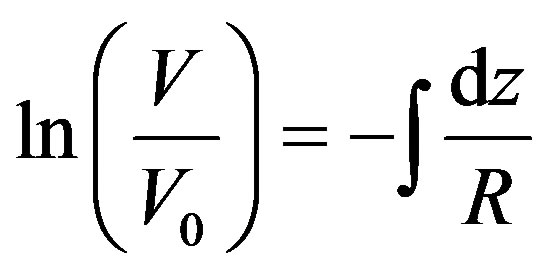 (5)
(5)
where V0 is a constant. Now both sides of Eq.5 can be raised to the exponential power to find
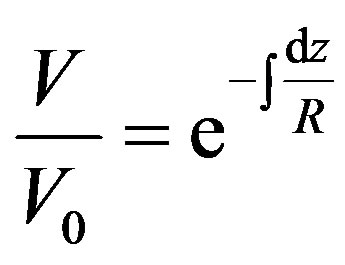 (6)
(6)
Go back to the starting point of Eq.1 and Eq.2 and eliminate V between them to get the pressure equation. What will be found is an equation very similar to Eq.4, with p replacing V, except for one important difference: a factor of 2 on the RHS in the numerator. That factor of 2 translates to a factor of 2 in the exponent of the pressure solution analogous to Eq.6. The disparity in decay rates between pressure and velocity stems from this factor of 2, and it can then be deduced that pressure variations decay faster than velocity variations with increasing distance down from the crest, without even knowing what the exact curvature function is.
In general Eq.6 should have another constant term following the integration, which for the present purposes is not needed. One constraint that helps evaluate the constants in Eq.6 is the fact that at great depth below the wave surface the velocity is constant.
Even without specific knowledge of the radius of curvature function it can be guessed that the odds are very small that the velocity and pressure in will turn out to have a typical exponential decay rate. Another feature of the solutions is that the pressure and velocity variations are not sensitive to the particular path R (z) takes between its minimum value at the surface and infinity at great depth due to the integrations involved on the RHS of these equations.
3. DISCUSSION
In the above calculation the z-axis was picked to have its origin at the top of a crest. There is no reason why the position of the z-axis could not have been placed in the center of a trough, because then a very similar calculation is easily constructed. After doing that the constant V0 can be determined by conserving mass between two vertical cross-sections, one at a crest and the other an adjacent trough. Then the constant p0 can be found also.
Further development of the above calculation depends critically on the radius of curvature function, R (z), which is not known yet from data or a priori from theory. In the steady reference frame streak photographs will undoubtedly show that the radius of curvature of the streamlines monotonically increases from the minimum value at a crest, for example, to infinity at depths exceeding approximately one wavelength. If such streak photographs do not exist already, it may not be too difficult of an experimental job to produce them. Then an algebraic function, which closely imitates the observed curvature function, can be inserted into the governing equations for pressure and velocity and the solution obtained analytically. Even if the curvature function is better expressed numerically, the governing equations are readily solvable because they are linear.
After completing the above mentioned work, which is left for the future, the general results stated in the abstract will not change qualitatively: the depth decay rates are different for pressure and velocity. Pressure variations decay faster than velocity variations and neither one will have the normal exponential form in all likelihood. These results squarely contradict the corresponding ones in the classical literature on the subject. Measurements will be needed to distinguish between the different predictions of the two theoretical methods. When only the one theory existed, apparently there was no strong impulse to check the exponential decay rate with careful observations of pressure and velocity, and no reported discrepancies or agreements with theory have been published, as far as I am aware. Exponential decay has been swallowed whole in the past.
An application of the above method can be made to the problem of calculating the decay rate of the steady flow past a cylinder, and it is even a bit simpler because to start with the gravity term in Eqs.1 and 2 can be dropped out. What will be found is that the pressure variation decays faster above (and below) the top of the cylinder than does the velocity variation. Again, this result appears to be a new one in fluid dynamics. And at least one text book has a streak photograph from which the radius of curvature function might be estimated.
4. CONCLUSION
A qualitative prediction is made for the depth decay rates of the pressure and velocity variations associated with surface gravity waves. Pressure should decay downward faster than velocity and neither decay rate should have the standard exponential form. The prediction is based upon two elementary pieces of physics: Bernoulli’s equation for steady frictionless flow along a streamline and the cross-stream force balance involving three forces, centrifugal, gravity and a pressure gradient. Pressure and velocity variations are governed by linear first order ordinary differential equations and are therefore solvable, either analytically or numerically. There is a non-constant coefficient that needs to be supplied to these equations from measurements (or some other theory): the radius of curvature of the streamlines as a function of depth. The solutions will not be sensitive to the actual path the radius of curvature takes between its minimum value at the surface and infinity at great depth. Observations will eventually decide which theoretical picture is more correct, the present one or the classical one.
REFERENCES
- Cook, A. and Halley, E. (1998) Charting the heavens and the seas. Clarenden Press, Oxford, 242.
- Stokes, G.G. (1847) On the theory of oscillatory waves. Transactions of the Cambridge Philosophical Society, 8, 441.
- Sverdrup, H.U., Johnson, M.W. and Fleming, R.H. (1942) The oceans. Prentice-Hall, New Jersey, 520-521.
- Kenyon, K.E. (1983) On the depth of wave influence. Journal of Physical Oceanography, 13, 1968-1970. doi:10.1175/1520-0485(1983)013<1968:OTDOWI>2.0.CO;2
- Kundu, P.K. (1990) Fluid mechanics. Academic Press, San Diego, 273.

