Natural Science
Vol.4 No.8A(2012), Article ID:21658,4 pages DOI:10.4236/ns.2012.428085
Derivation of the Gutenberg-Richter empirical formula from the solution of the generalized logistic equation
![]()
1Aims College, Greeley, USA; *Corresponding Author: lev.maslov@aims.edu
2Computer Center Far Eastern Branch Russian Academy of Science, Khabarovsk, Russia
3All-Russia Research Institute for Geology and Mineral Resources of the Ocean (VNIIOKEANGEOLOGIA), St. Petersburg, Russia
Received 11 June 2012; revised 10 July 2012; accepted 27 July 2012
Keywords: Gutenberg-Richter Formula; Generalized Logistic Equation; Earthquakes
ABSTRACT
We have written a new equation to study the statistics of earthquake distributions. We call this equation “the generalized logistic equation”. The Gutenberg-Richter frequency-magnitude formula was derived from the solution of the generalized logistic equation as an asymptotic case for the approximation of large magnitude earthquakes. To illustrate how the solution of the generalized logistic equation works, it was used to approximate the observed cumulative distribution of earthquakes in four different geological provinces: the Central Atlantic (40N - 25N, 5W - 35W), Canary Islands, Magellan Mountains (20N - 9S, 148E - 170E), and the Sea of Japan. This approximation showed an excellent correlation between the theoretical curves and observed data for earthquakes of magnitudes 1 < m < 9.
1. INTRODUCTION
Earthquakes and volcanic eruptions are very complex phenomena and are caused by many different processes taking place both inside the Earth and very far outside its outer boundaries.
Many of these processes are very poorly understood. In this case, a phenomenological study of regularities in the distribution of earthquakes and faults, based on well formulated and mathematically expressed physical models, can provide insight into the physics and kinetics of earthquake processes. An example of this approach is the empirical relation [1] between the magnitude and frequency of earthquakes obtained by Ishimoto, M. and Iida, K., which initiated the study of earthquakes as self-organized critical phenomena. The empirical expression, similar to that obtained in [1], was published by R. Gutenberg and C. F. Richter three years later, [2]. In the current research we traditionally refer to this relation as the “Gutenberg-Richter magnitude-frequency formula”: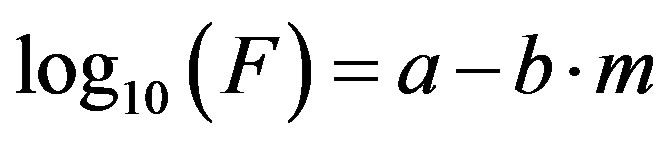 . Here F represents frequency, m represents magnitude, and a and b are constants. The discovery of this formula sparked the study of earthquakes in various fields including statistical physics, fractal mathematics, and mathematics of self-organized criticality [3], which continues to this day [4]. The other, more technical problem, attracting the attention of scientists, is the study of the spacial and temporal variation of the coefficient b. It was found in numerous studies [5-8] that this coefficient, supposedly a fundamental seismologics constant, varies significantly in space and time. It was shown also that the linear relation holds only for magnitudes m in a certain range, approximately 4 ≤ m. This implies that the Gutenberg-Richter magnitude-frequency empirical formula is not a “fundamental law”, but part of a more general relation between the frequency of earthquakes and their magnitudes (or seismic moment).
. Here F represents frequency, m represents magnitude, and a and b are constants. The discovery of this formula sparked the study of earthquakes in various fields including statistical physics, fractal mathematics, and mathematics of self-organized criticality [3], which continues to this day [4]. The other, more technical problem, attracting the attention of scientists, is the study of the spacial and temporal variation of the coefficient b. It was found in numerous studies [5-8] that this coefficient, supposedly a fundamental seismologics constant, varies significantly in space and time. It was shown also that the linear relation holds only for magnitudes m in a certain range, approximately 4 ≤ m. This implies that the Gutenberg-Richter magnitude-frequency empirical formula is not a “fundamental law”, but part of a more general relation between the frequency of earthquakes and their magnitudes (or seismic moment).
The main objective of the present work is to derive the Gutenberg-Richter magnitude-frequency empirical formula from the solution of the generalized logistic equation and to illustrate its usage by modeling cumulative earthquake distributions in four different geological provinces.
2. THE GENERALIZED LOGISTIC EQUATION
Let us consider the equation:
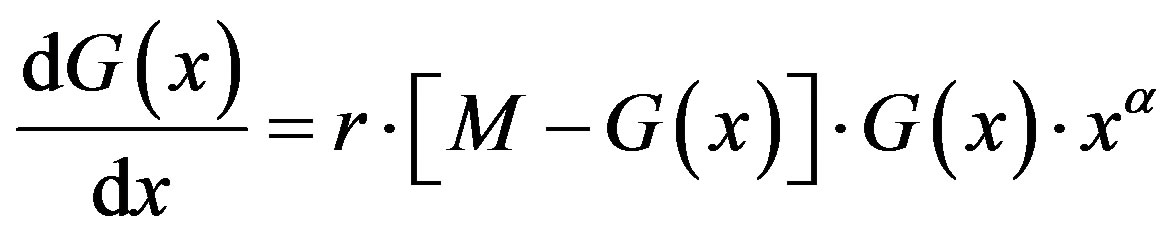 (1)
(1)
with respect to the function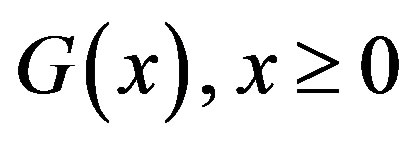 , where
, where 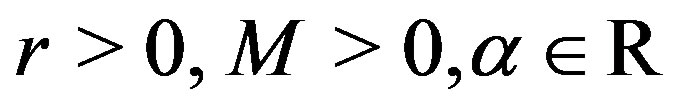 , are some parameters. This equation differs from the classical logistic equation only by the multiple
, are some parameters. This equation differs from the classical logistic equation only by the multiple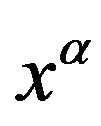 .
.
Let
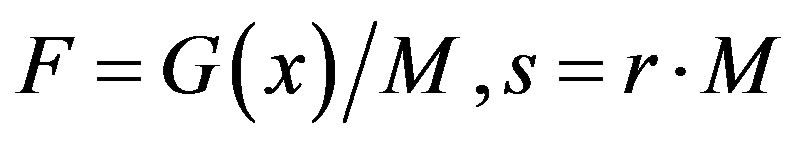 then, Equation (1) becomes
then, Equation (1) becomes
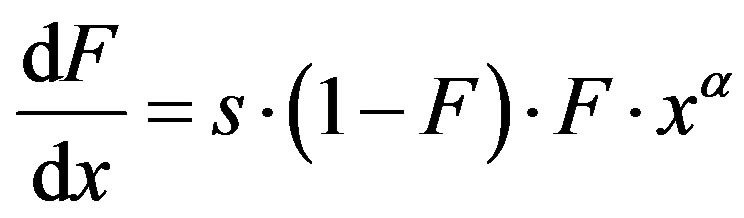 . (1a)
. (1a)
The boundary condition is
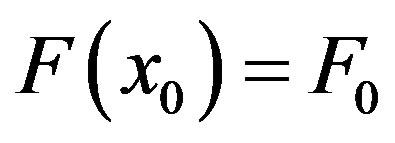 . (1b)
. (1b)
The solution to the problem (1a), (1b) for 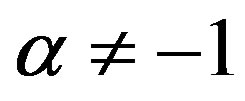 is:
is:
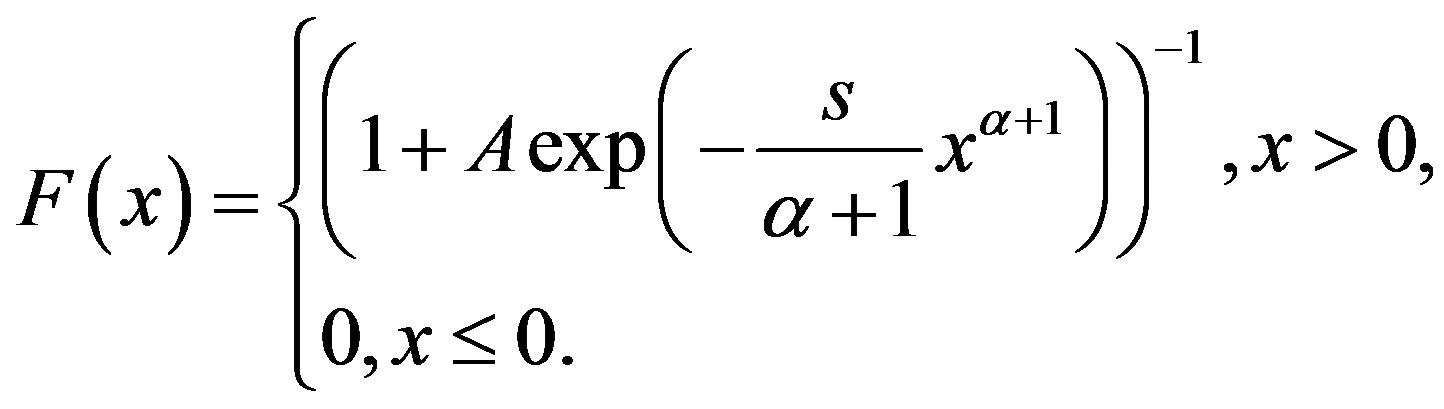 (2)
(2)
For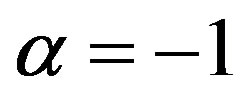 , the solution of (1a) and (1b) is
, the solution of (1a) and (1b) is
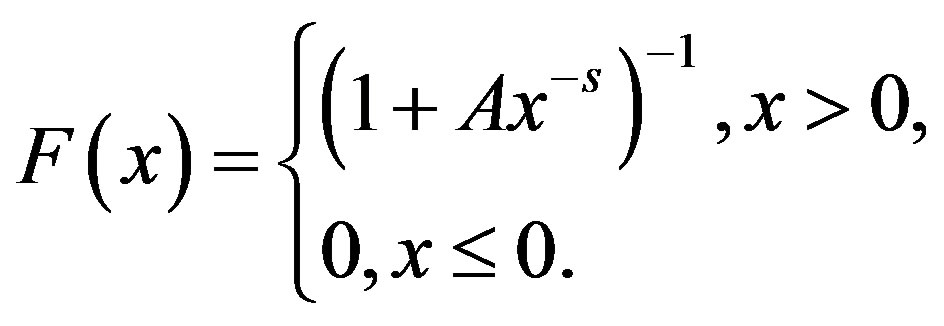 , (3)
, (3)
and for  in (2) we have
in (2) we have

 . (4)
. (4)
The constant A in (2), (3) and (4) can be found using the boundary condition (1b).
The derivative of (2) for x > 0 is
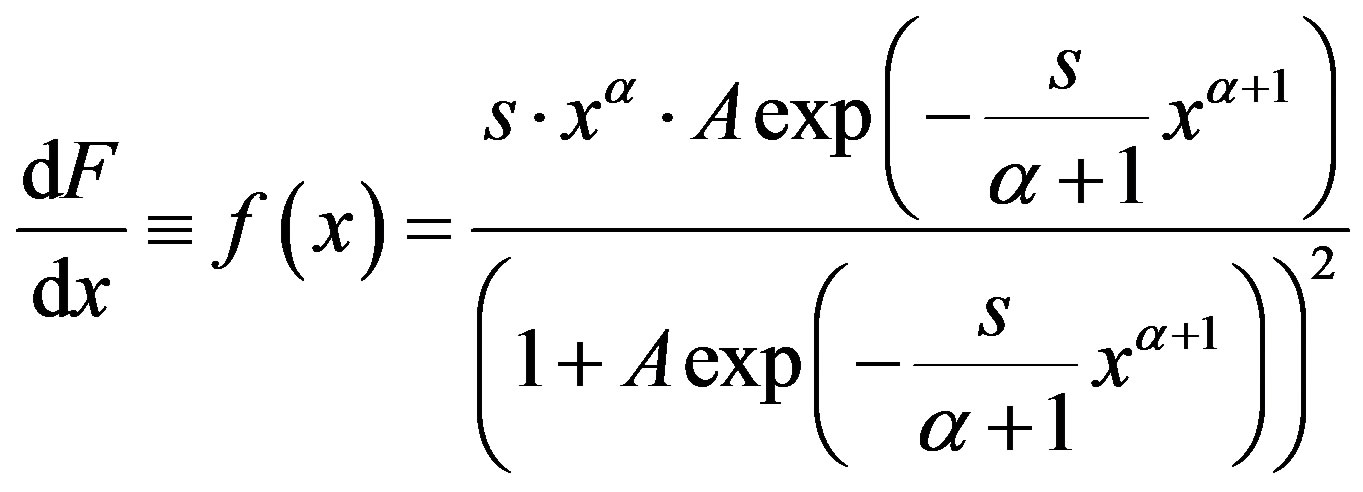 (5)
(5)
Thus, the solutions of Equation (1a) for 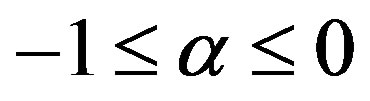 are a set of functions distributed from log-logistic to logistic.
are a set of functions distributed from log-logistic to logistic.
3. THE GUTENBERG-RICHTER FORMULA
The Gutenberg-Richter relation between the number of earthquakes with magnitudes ≥ m written for the natural logarithm is:
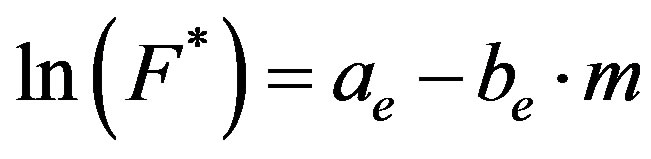 , (6)
, (6)
where F is the frequency, and m is the magnitude of earthquakes. This formula can be rewritten as
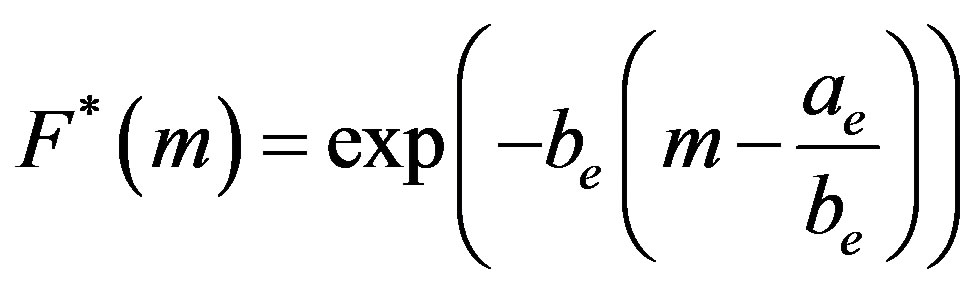 . (7)
. (7)
which is the well-known exponential distribution shifted by the value of 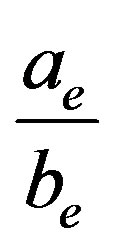 .
.
The same expression as (7), but for magnitudes ≤ m has the form
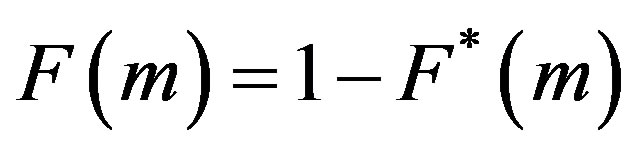 . (8)
. (8)
Thus, (6)-(8) are equivalent forms of the GutenbergRichter formula. An example of this approximation of the earthquake data by an exponential distribution is shown in Figure 1.
This figure clearly shows that the Gutenberg-Richter formula is the part of the more general law relating earthquake frequency and magnitude. This graph works in favor of the conclusion made by many authors [5-8] that the best correlation between the Gutenberg-Richter relation and earthquake distributions is observed for large magnitudes, approximately greater than 4.0.
4. DERIVATION OF THE GUTENBERG-RICHTER FORMULA FROM THE SOLUTION OF THE GENERALIZED LOGISTIC EQUATION
To compare (2) and (7) let us rewrite (2) in a form (8) for x > 0
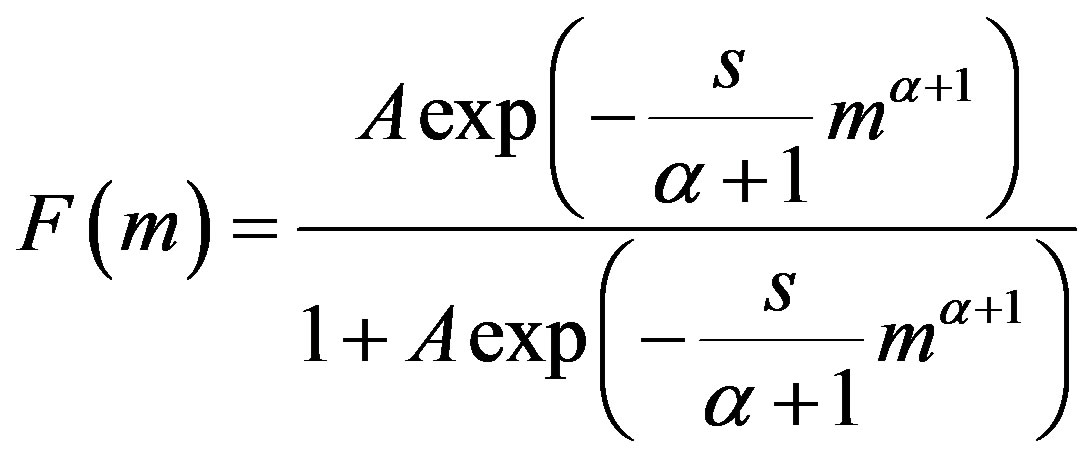 . (9)
. (9)
Using an expansion of (9) in powers of 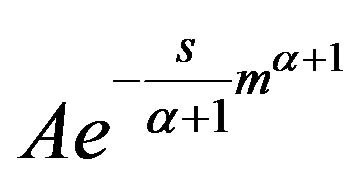 we obtain
we obtain

Figure 1. The exponential distribution function calculated by formula (8), green; solution (2) of Equation (1a), red, and observed Magellan Mountains cumulative earthquake distributions, crosses. The Gutenberg-Richter b-value, calculated from approximating exponential curve is 1.3.
 , (10)
, (10)
and
 . (11)
. (11)
Putting in (11)  we arrive at the Gutenberg-Richter formula (6a). Expression (11) can be considered as a generalized Gutenberg-Richter formula.
we arrive at the Gutenberg-Richter formula (6a). Expression (11) can be considered as a generalized Gutenberg-Richter formula.
5. APPLICATION OF THE SOLUTION OF THE GENERALIZED LOGISTIC EQUATION FOR MODELING CUMULATIVE DISTRIBUTION OF EARTHQUAKES
To illustrate the application of solution (2) for modeling the cumulative distribution of earthquakes, we picked four different geological provinces: Central Atlantic, Canary Islands, Magellan Mountains, and the Sea of Japan. In addition to solution (2), the following statistical functions were used to approximate the observed data: the Gamma-distribution, the Weibull distribution, the log-normal, logistic, and log-logistic distributions. Figure 2 shows the observed cumulative normalized distribution of earthquakes with magnitudes ≤ m (crosses), and graphs of functions calculated from formulas (2) and (5): cumulative distribution (red), and the probability density function (blue).
The accuracy of our approximation was estimated by using an  test for accuracy of fit with confidence level 0.05. It was found that the best approximation of the observed data for magnitudes 1 < m < 8 was provided with distribution (2), and as in case of the Central
test for accuracy of fit with confidence level 0.05. It was found that the best approximation of the observed data for magnitudes 1 < m < 8 was provided with distribution (2), and as in case of the Central
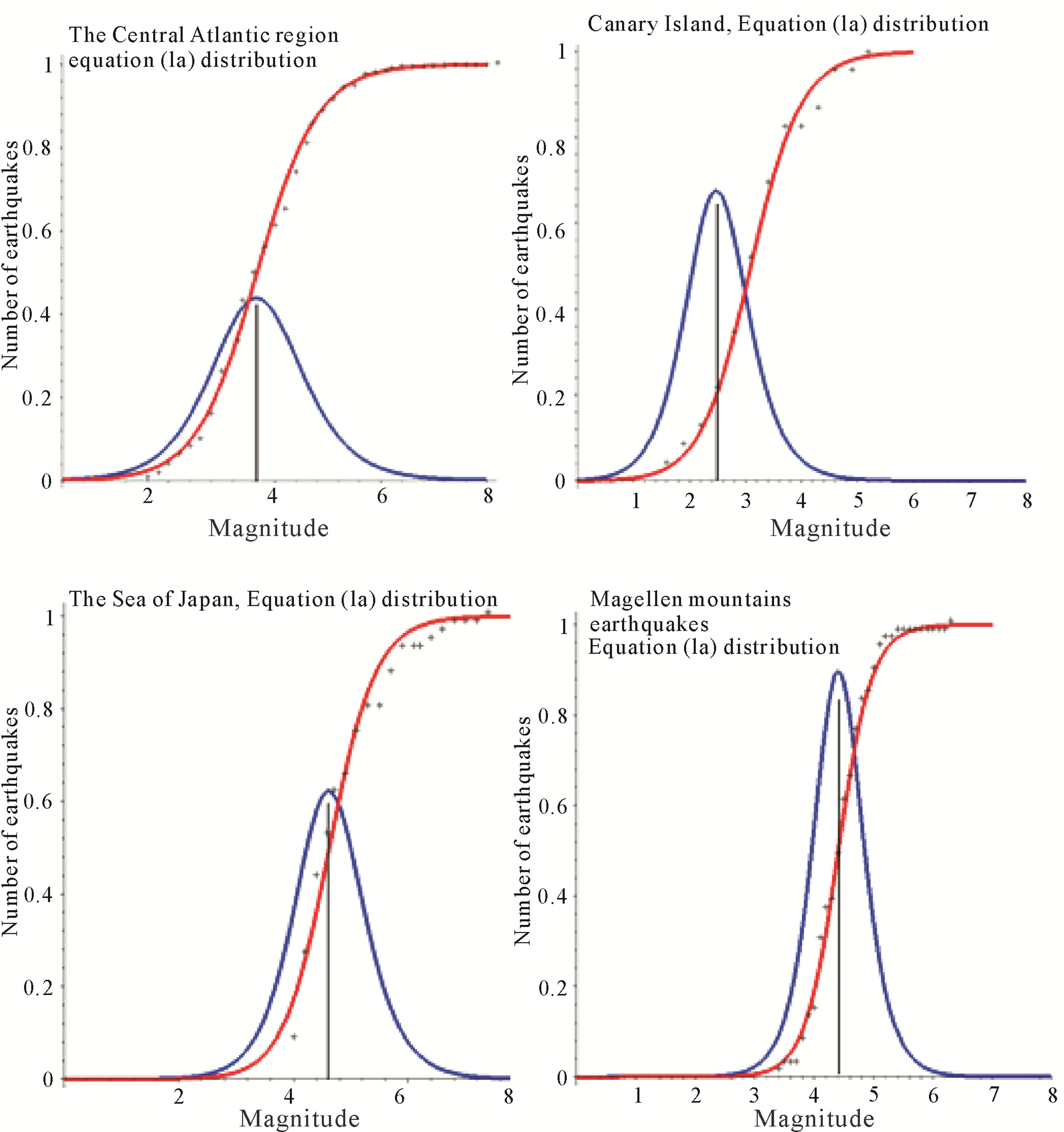
Figure 2. The observed cumulative normalized distribution of earthquakes (crosses), theoretical cumulative distribution (red), and probability density function (blue).
Atlantic for magnitudes 1 < m < 9. Future research can specify the limits of application of Equations (2) and (3) for modeling earthquake distributions.
6. DISCUSSION
The coefficient b,
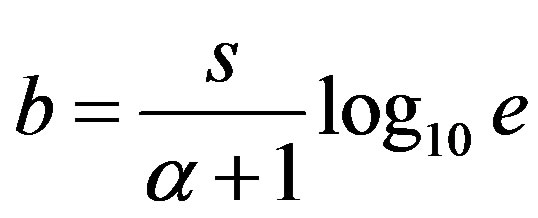 , (12)
, (12)
analogous to the Gutenberg and Richter b-value, was calculated for each area, considered in this work, using the coefficients s and α of the function (2) approximating the observed cumulative distribution of earthquakes, Figure 2.
The Table 1 summarizes this calculation. This Table also shows the expected magnitudes of earthquakes taken from the probability distribution functions of these areas, Figure 2.
The Gutenberg-Richter b-value calculated for the Magellan Mountains region is 1.3. The coefficient b, calculated for this region by formula (12), is 1.8. This difference can be explained by the fact that the exponential function approximates the observed distribution for magnitudes m > 4 only, while the coefficient b was calculated by the formula (12) with coefficients s and α obtained for the whole curve, approximating a range of earthquake magnitudes, from 1 to 9.
The excellent fit between the observed data and the solution of the generalized logistic equation, presented in this work, indicates that this equation can become a new starting point in understanding the physics of earthquakes and constructing statistical models explaining the spacial and temporal distribution of earthquakes.
7. DATA
All the data used in this work were taken from the US Geological Survey Earthquake Data Base website: http://www.earthquake.USGS.gov/earthquakes/eqarchives/epic/epic_rest.php.
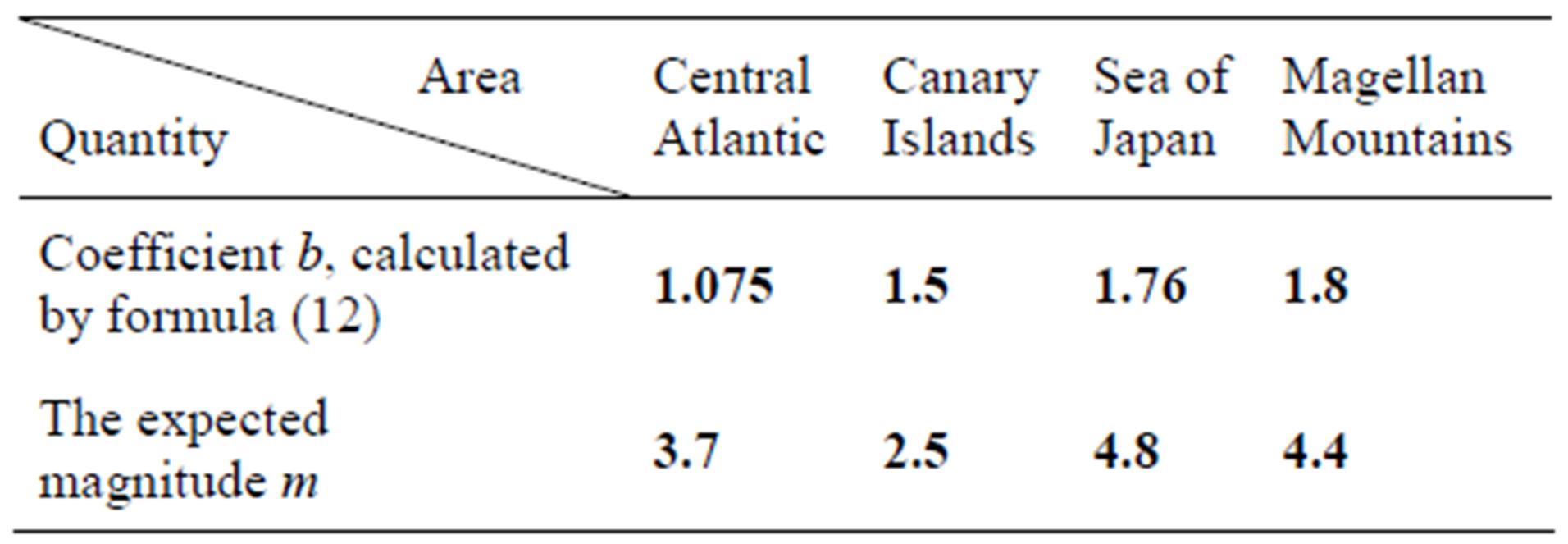
Table 1. Coefficient b, calculated by formula (12), and expected magnitudes of earthquakes calculated by formula (5).
8. CONCLUSIONS
The Gutenberg-Richter frequency-magnitude formula was derived as an asymptotic case for large magnitude earthquakes from the solution of the generalized logistic equation.
Approximation of the observed cumulative distribution of earthquakes was given for four different geological provinces: in the Central Atlantic (40N - 25N, 5W - 35W), Canary Islands, Magellan Mountains (20N - 9S, 148E - 170E), and the Sea of Japan. The solution of the generalized logistic equation showed an excellent fit between the theoretical and observed data for magnitudes 1 < m < 9.
The new approach to the modeling and study of earthquakes, presented in this work, can provide us with new insight into the physics of earthquakes.
9. ACKNOWLEDGEMENTS
Authors are grateful to Prof. V. I. Chebotarev for his comments and suggestions which helped to improve the quality of this work.
REFERENCES
- Ishimoto, M. and Iida, K. (1939) Observations sur les seismes enregistres parle microsismographe construit dernierement (1). Bulletin of the Earthquake Research Institute, 17, 443-478.
- Gutenberg, B. and Richter, C.F. (1942) Earthquake magnitude, intensity, energy and acceleration. Bulletin of the Seismological Society of America, 32, 163-191.
- Main, I. (1996) Statistical physics, seismogenesis, and seismic hazard. Reviews of Geophysics, 34, 433-462. doi:10.1029/96RG02808
- Bundle, J.B., Turcott, D.L., Shcherbakov, R., Klein, W., Sammis, C. (2003) Statistical physics approach to understanding the multiscale dynamics of earthquake fault system. Reviews of Geophysics, 41, 1-30.
- Ayele, A. and Kulhanek, O. (1997) Spatial and temporal variation of seismicity in the horn of Africa from 1960 to 1993. Geophysical Journal International, 130, 805-810. doi:10.1111/j.1365-246X.1997.tb01875.x
- Gerstenberger, M., Wiemer, S. and Gardini, D. (2001) A systematic test of the hypothesis that the b-value varies with depth in California. Geophysical Research Letters, 28, 57-60. doi:10.1029/2000GL012026
- Gibowicz, S.J. and Lasocki, S. (2001) Seismicity induced by mining: Ten years later. In: Dmowska, R. and Saltzman, B., Eds., Advances in Geophysics, Academic Press, Academic Press, 39-181.
- Smyth, C. and Mori, J. (2009) Temporal variations of the Gutenberg-Richter distribution prior to the Kobe earthquake. Annals of Disaster Prevention Research Institute, 52B, 255-261.

