Natural Science
Vol.4 No.10(2012), Article ID:23950,5 pages DOI:10.4236/ns.2012.410105
Resonance Raman spectroscopy of red blood cells using lie algebraic technique
![]()
1Department of Mathematics, Jawaharlal Nehru Technological University Kakinada, Kakinada, India; *Corresponding Author: vsjaliparthi@gmail.com
2Department of Electronics & Instrumentation Engineering, Lakireddy Bali Reddy College of Engineering, Vijayawada, India
3Department of Applied Mathematics, College of Science & Technology, Andhra University, Visakhapatnam, India
Received 8 April 2012; revised 15 May 2012; accepted 30 May 2012
Keywords: Raman Spectroscopy; Red Blood Cell; Lie Algebraic Technique; Vibrational Assignments
ABSTRACT
Raman spectra of oxygenated and deoxygenated functional erythrocytes are calculated by using Lie algebraic technique. The results are obtained by this method is accuracy with the experimental data. So, the algebraic techniques are appropriate to the Raman spectra of red blood cells.
1. INTRODUCTION
To maintain resonance with the rapid development of sophisticated experimental approaches, theoretical physics has been constantly tested to provide a collection of satisfactory models that can account for the experimental observations [1-4]. Characterizing these experimental data is equally important for understanding the dynamics of chemical reactions and structure of these molecules. The model is based on the idea of dynamical symmetry, which is expressed through the language of Lie algebras. Applying algebraic techniques, we obtain an effective Hamiltonian operator that conveniently describes the rotational vibrational degrees of freedom of the physical system.
The algebraic model (Vibron model) was originally developed for diatomic and tri-atomic molecules [5-8]. It is to be pointed out that the U (4) model becomes complicated when the number of atoms in a molecule increases more than four. The Vibron model was applied successfully in describing the overtone frequencies of linear and bent X2Y molecules. Later, it was extended to linear and quasi-linear tetratomic molecules and could prove itself to be a competitive one to the traditional analysis. The main features and basic applications of these methods have been described by Iachello and Levine and Oss [9]. The brief review of the research work done in this field up to 2000 and its perspectives in the first part of 21st century was presented by Iachello and Oss [10]. Lie algebraic approach was found to be successful in our study of vibrational frequencies of HCN, HCCF, HCCD, tetrahedral and Porphyrins molecules [11-20].
In this paper, we have calculated the vibrational energy levels of oxygenated and deoxygenated functional erythrocytes at 785 nm for 15 vibrational bands by using Lie algebraic mode Hamiltonian.
2. REVIEW OF THE THEORY
2.1. An Algebraic Techniques
First, The algebraic theory of polyatomic molecules consists in the separate quantization of rotations and vibrations in terms of vector coordinates r1, r2, r3,··· quantized through the algebra

For the stretching vibrations of polyatomic molecules correspond to the quantization of anharmonic Morse oscillators, with classical Hamiltonian
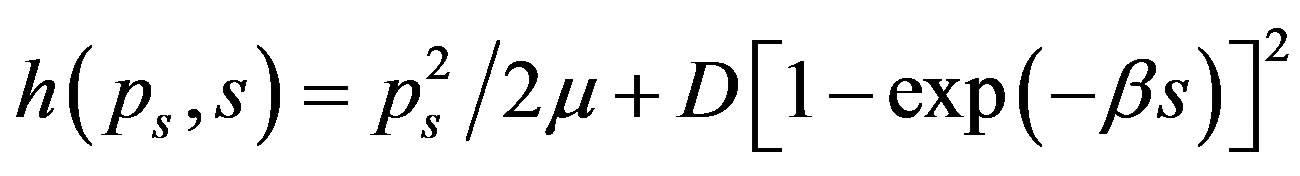 (1)
(1)
For each oscillator i, states are characterized by representations of
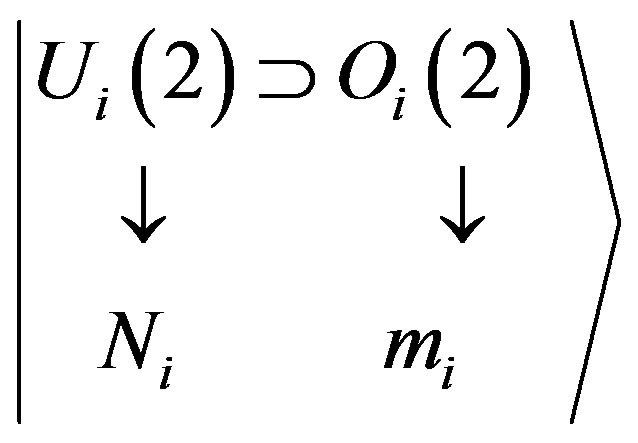 (2)
(2)
with mi = Ni, Ni – 2, ···, 1 or 0 (Ni—odd or even). The Morse Hamiltonian (1) can be written, in the algebraic approach, simply as
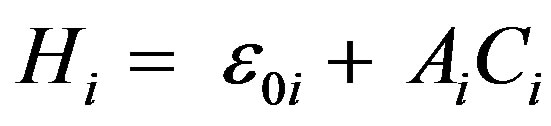 (3)
(3)
where Ci is the invariant operator of Oi (2), with eigen values
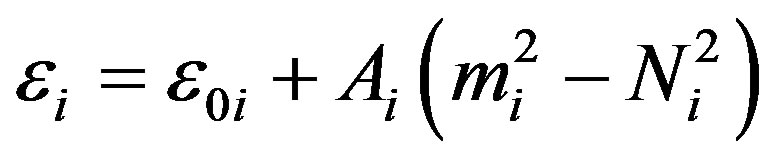
Introducing the vibrational quantum number νi =(Ni – mi)/2, [9] one has
 (4)
(4)
For non-interacting oscillators the total Hamiltonian is
 with eigenvalues
with eigenvalues
 (5)
(5)
2.2. Hamiltonian for Stretching Vibrations
The interaction potential can be written as
 (6)
(6)
which reduce s to the usual harmonic force field when the displacements are small
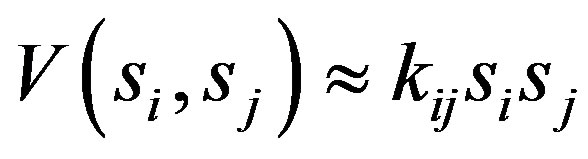
Interaction of the type Equation (6) can be taken into account in the algebraic approach by introducing two terms [9].One of these terms is the Casimir operator, Cij, of the combined  algebra. The matrix elements of this operator in the basis Equation (2) are given by
algebra. The matrix elements of this operator in the basis Equation (2) are given by
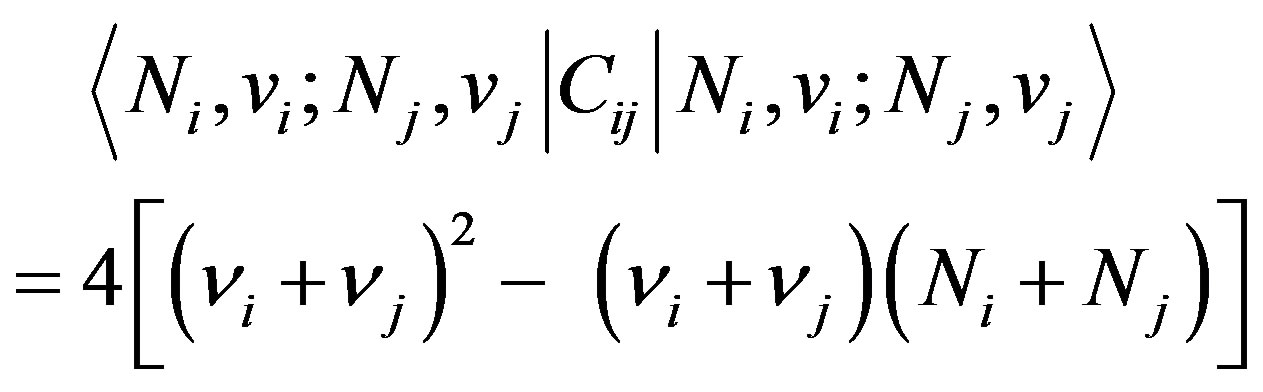 (7)
(7)
The operator Cij is diagonal and the vibrational quantum numbers νi have been used instead of mi. In practical calculations, it is sometime convenient to substract from Cij a contribution that can be absorbed in the Casimir operators of the individual modes i and j, thus considering an operator 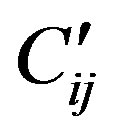 whose matrix elements are
whose matrix elements are
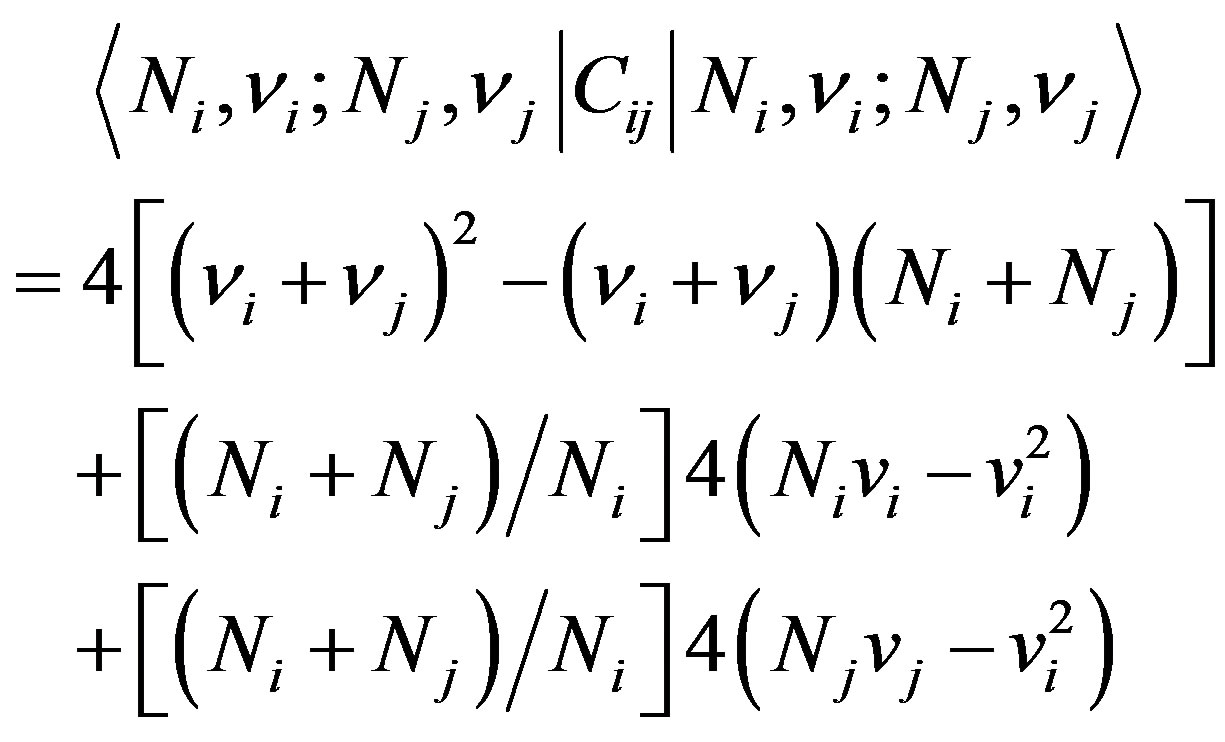 (8)
(8)
The second term is the Majorana operator, Mij. This operator has both diagonal and off-diagonal matrix elements
 (9)
(9)
The Majorana operators Mij annihilâtes one quantum of vibration in bond i and create one in bond j, or vice versa.
The total Hamiltonian for n stretching vibrations is
 (10)
(10)
If λij = 0 the vibrations have local behavior. As the λij increase, one goes more and more into normal vibrations.
By inspection of the figure, one can see that two types of interactions in the molecule:
1) First-neighbor couplings (Adjacent interactions);
2) Second-neighbor couplings (Opposite interactions).
The symmetry-adapted operators of molecule with symmetry D4h are those corresponding to these two couplings, that is,
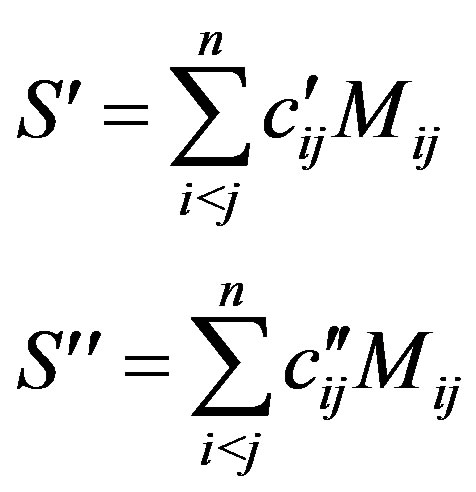 (11)
(11)
with
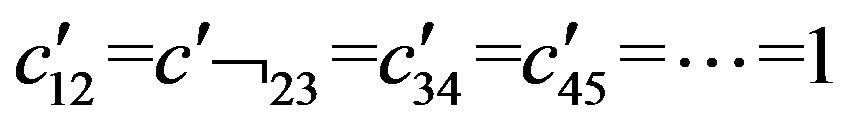


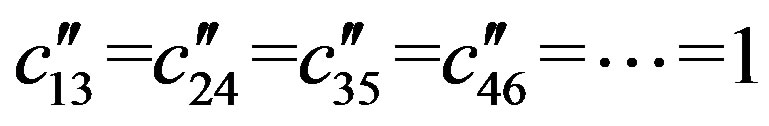
The total Majorana operator S is the sum
 (12)
(12)
Diagonalization of S produces states that carry representations of S, the group of permutations of objects, while diagonalization of the other operators produces states that transform according to the representations A1g, A2g, B1g, B2g, E1u of D4h.
3. RESULTS AND DISCUSSIONS
The number N [total number of bosons, label of the irreducible representation of U (2)] is related to the total number of bound states supported by the potential well. Equivalently it can be put in a one-to-one corresponddence [11-19] with the anharmonicities parameters xe by means of
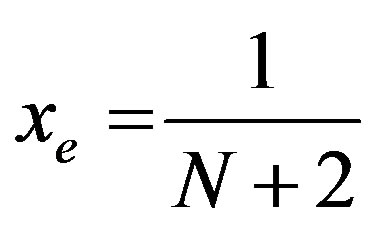 (13)
(13)
We can rewrite the Equation (13) as
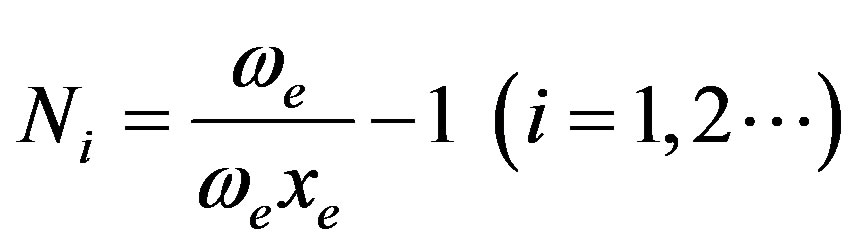 (14)
(14)
Now, for a blood cell molecule, we have the values of ωe and ωe xe for the distinct bonds (say CH, CC, CD, CN etc) from the study of K. Nakamoto [21] and that of K. P. Huber and G. Herzberg [22]. Using the values of ωe and ωe xe for the bond CH/CC we can have the initial guess for the value of the vibron number N.
Depending on the specific molecular structure Ni can vary between ±20% of the original value. The vibron number N between the diatomic molecules C-H and C-C are 44 and 140 respectively. Since the bonds are equivalent, the value of N is kept fixed. This is equivalent to change the single-bond anharmonicity according to the specific molecular environment, in which it can be slightly different.
Again the energy expression for the single-oscillator in fundamental mode is
 (15)
(15)
In the present case we have three and six different energies corresponding to symmetric and antisymmetric combinations of the different local mode.
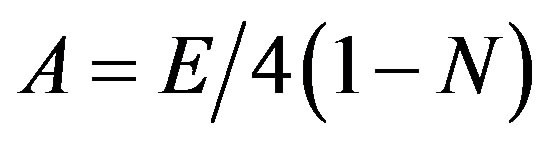 (16)
(16)
The initial guess for λ can be obtained by
 (17)
(17)
A numerical fitting procedure is adopted to adjust the parameters A and λ starting from the values above and A′ whose initial guess can be zero. The complete calculation data in stretching and bending modes are presented in Table 1 and the corresponding algebraic parameters are presented in Table 2.
4. CONCLUSIONS
Using the algebraic model for local to normal transition here we presented a study of Raman spectra of Oxynated and Deoxynated red blood cell molecules. On the basis of the results reported here, we have the conclusion of our study as follows:
In the study of resonance Raman spectra of Oxynated red blood cell molecule for 16 vibrational bands we obtain Δ (r.m.s) as 7.7892 cm–1.
In the study of resonance Raman spectra of Deoxynated red blood cell molecule for 16 vibrational bands we obtain Δ (r.m.s) as 10.623 cm–1.
Using improved set of algebraic parameters, the RMS deviation we reported in this study for Oxynated and
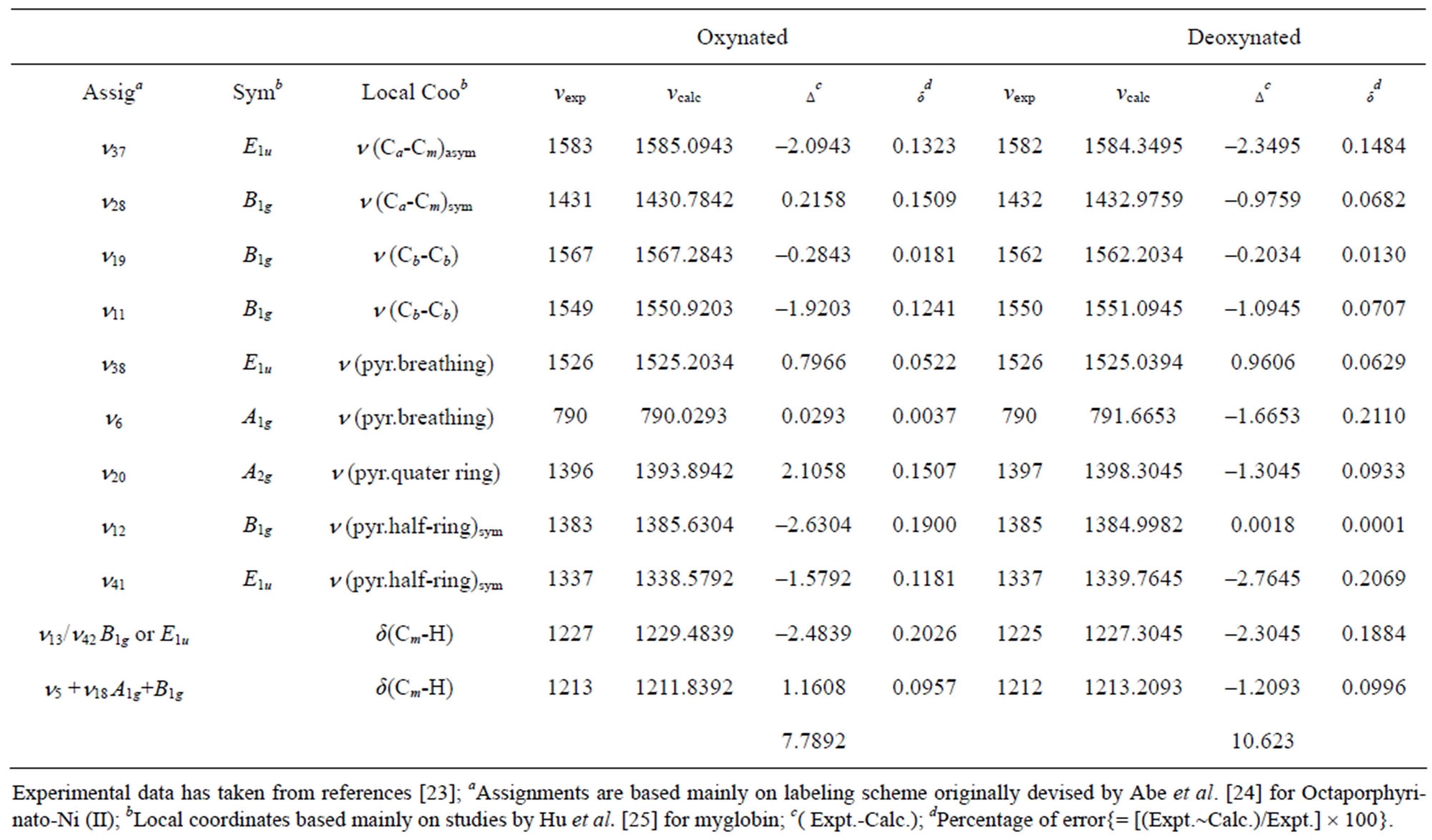
Table 1. Comparison between experimental and calculated resonance Raman bands of oxynated and deoxynated cells (cm−1).

Table 2. Valuese of the algebraic parameters used in the calculation of red blood cell molecule.
Deoxynated red blood cell molecule is lying near about the experimental accuracy. Using only four algebraic parameters, the RMS deviation we reported in this study for red blood cell molecule are good fit. Percentage error corresponding to each of the calculated vibrational energy levels of red blood cell we reported in this study is practically zero.
We hope that this work will stimulate further research in analysis of resonance Raman spectra of isotopes of other red blood cell molecules where the algebraic approach has not been applied so far. The research work concern is in progress, which is one can also discuss the spectroscopic properties and isotopes effects of red blood cell molecules with this algebraic Hamiltonian.
5. ACKNOWLEDGEMENTS
The author Srinivasa Rao Karumuri also would like to thank The Department of Science & Technology, New Delhi, India, for providing the financial assistance for this study. The author is very thankful to the anonymous referee of this paper for valuable suggestions and comments, which greatly helped to improve the quality of this paper.
REFERENCES
- Wood, B.R., Hammer, L., Davis, L. and McNaughton, D. (2005) Raman microspectroscopy and imaging provides insights into heme aggregation and denaturation within human erythrocytes. Journal of Biomedical Optics, 10, 14005. doi:10.1117/1.1854678
- Spiro T.G., Ed. (1988) The biological application of Raman spectroscopy. Wiley, New York.
- Puppels, G.J., Olminkhof, J.H.F., Segers-Nolten, G.M.J., Otto, C., de Mul, F.F.M. and Greve, J. (1991) Laser radiation and Raman spectroscopy of single living cells and Chromosomes: Sample degration occurs with 514.15 nm but not with 600 nm laser light. Experimental Cell Research, 195, 361-367. doi:10.1016/0014-4827(91)90385-8
- Van Manen, H.-J., Kraan, Y.M., Roos, D. and Otto, C. (2004) Single-cell Raman and fluorescence microscopy reveal the association of lipid bodies with phagosomes in leukocytes. The Journal of Physical Chemistry B, 108, 18762-18771. doi:10.1021/jp046955b
- Iachello, F. (1981) Algebraic methods for molecular rotational-vibrational spectra. Chemical Physics Letters, 78, 581. doi:10.1016/0009-2614(81)85262-1
- Iachello, F. and Levine, R.D. (1982) Algebraic approach to molecular rotation and vibration spectra-I diatomic molecules. Journal of Chemical Physics, 77, 3046. doi:10.1063/1.444228
- van Roosmalen, O., Dieperink, A.E.L. and Iachello, F. (1982) A dynamic algebra for molecular rotation-vibration spectra of complex molecules. Chemical Physics Letters, 85, 32-36. doi:10.1016/0009-2614(82)83455-6
- van Roosmalen, O., Iachello, F., Levine, R.D. and Dieperink, A.E.L. (1983) Algebraic approach to molecular spectra of rotation-vibration-II: Triatomic molecules, Journal of Chemical Physics, 79, 2515.
- Iachello, F. and Levine, R.D. (1996) Algebraic theory of molecules. Advances in Chemical Physics, 93, 455.
- Iachello, F. and Oss, S. (2002) Algebraic methods in quantum mechanics: From molecules to polymers, European Physical Journal D, 19, 307. doi:10.1140/epjd/e20020089
- Sarkar, N.K., Choudhury, J., Karumuri, S.R. and Bhattacharjee, R. (2008) An algebraic approach to the comparative study of the vibrational spectra of monofluoroacetylene (HCCF) and deuterated acetylene (HCCD). Molecular Physics, 106, 693-702. doi:10.1080/00268970801939019
- Sarkar, N.K., Choudhury, J., Karumuri, S.R. and Bhattacharjee, R. (2009) A Comparative study of the vibrational spectra of OCS and HCP using lie algebraic method, European Physical Journal D, 53, 163. doi:10.1140/epjd/e2009-00094-8
- Choudhury, J., Karumuri, S.R., Sarkar, N.K. and Bhattacharjee, R. (2009) Vibrational spectroscopy of CH/CD stretches of propadiene: An algebraic approach, Chinese Physics Letters, 26, 020308. doi:10.1088/0256-307X/26/2/020308
- Choudhury, J., Karumuri, S.R., Sarkar, N.K. and Bhattacharjee, R. (2008) Vibrational spectroscopy of CCl4 and SnBr4 using lie algebraic approach. Physics and Astronomy, 71, 439-445.
- Karumuri, S.R., Sarkar, N.K., Choudhury, J. and Bhattacharjee, R. (2008) Vibrational spectroscopy of Cm-H, Cb-Cb stretching vibrations of Nickel metalloporphyrins. Molecular Physics, 106, 1733-1738. doi:10.1080/00268970802248998
- Karumuri, S.R., Choudhury, J., Sarkar, N.K. and Bhattacharjee, R. (2008) Analysis of resonance raman spectra of nickeloctaethyl porphyrin using lie algebra. Journal of Environmental Research and Development, 3, 250-256.
- Karumuri, S.R., Sarkar, N.K., Choudhury, J. and Bhattacharjee, R. (2009) Study of vibrational spectra of Nickel metalloporphyrins: An algebraic approach. Pramana— Journal of Physics, 72, 517-525.
- Karumuri, S.R., Sarkar, N.K., Choudhury, J. and Bhattacharjee, R. (2009) Vibrational spectroscopy of stretching and bending modes of nickel tetraphenyl porphyrin: An algebraic approach. Chinese Physics Letters, 26, 93- 301. doi:10.1088/0256-307X/26/9/093301
- Karumuri, S.R., Sarkar, N.K., Choudhury, J. and Bhattacharjee, R. (2009) U(2) algebraic model applied to vibrational spectra of Nickel metalloporphyrins. Journal of Molecular Spectroscopy, 255, 183-188. doi:10.1016/j.jms.2009.03.014
- Karumuri, S.R. (2010) Calculation of vibrational spectra by an algebraic approach: Applications to copper tetramesityl porphyrins and its cation radicals. Journal of Molecular Spectroscopy, 259, 86-92. doi:10.1016/j.jms.2009.11.005
- Nakamoto, K. (1997) Infrared and Raman spectra of inorganic and coordination compounds (Part A: Theory and applications in inorganic chemistry). John wiley & Sons, Inc., Hoboken.
- Phuber, K. and Herzberg, G. (1979) Molecular spectra and molecular structure IV: Constants of diatomic molecules. Van Nostrand Reinhold Co., New York.
- Wood, B.R., Caspers, P. and Pupples, G.J. (2007) Molecular imaging of red blood cells by Raman spectroscopy, Analytical and Bioanalytical Chemistry, 387, 1691. doi:10.1007/s00216-006-0881-8
- Abe, M., Kitagawa, T. and Kyogoku, K. (1978), Resonance Raman spectra octaethylporphyrinato-II and meso deuterated and 15N substituted derivatives. I. A. Normal coordinate analysis. Journal of Chemical Physics, 69, 4526. doi:10.1063/1.436450
- Hu, S., Smith, K. M. and Spiro, T. G. (1996) Assignment of protoheme resonance Raman spectrum by heme lebeling in myglobine, Journal of the American Chemical Society, 118, 12638. doi:10.1021/ja962239e

