Health
Vol.09 No.03(2017), Article ID:74761,14 pages
10.4236/health.2017.93033
Resistive Factors of the Blood Flow and Energy Distribution in the Body
Guram Beraia1, Merab Beraia2
1Medical University, Tbilisi, Georgia
2Institute of Clinical Medicine, Tbilisi, Georgia

Copyright © 2017 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: February 12, 2017; Accepted: March 14, 2017; Published: March 17, 2017
ABSTRACT
Purpose of the study is to identify the reason for the formation of the resistive factors in blood flow: inertial flow and turbulence in large arteries and increasing viscosity in the venous blood. Methods and Materials: Blood flow velocities were studied in the different sites of the large vessels in 35 normal adults (15 men, 20 women, age 21 - 49 years) with the use of Magnetic Resonance Angiography. Blood radiodensity (HU) was measured by the CT scanner. Blood flow pulsatility, resistivity indexes were carried out with the Duplex US. Results: Resistive and pulsatility indexes for the ascending aorta are 0.96 ± 0.07 and 3.14. ± 1.7, abdominal aorta 0.91 ± 0.07 and 2.7 ± 1.3, carotid artery 0.74 ± 0.07 and 2.04 ± 0.53, pulmonary trunk 0.74 ± 0.11 and 1.49 ± 0.37, inferior vena cava 0.32 ± 0.21 and 0.69 ± 0.37. Blood radio density (in HU) in the ascending aorta is 57.3 ± 3.5, distal thoracic aorta 25.7 ± 3.1, and inferior vena cava 59.3 ± 3.3. Pulsation of the peak velocity is expressed at the external wall of the isthmus of aorta at the end of systole. Conclusion: Heart energy is stored in the elastic deformation of the blood cells and arterial walls, in kinetic energy of the blood flow, entropy of the system. Inertial blood flow due to the frequency dispersion in the arteries, transforms to the flow with the high fluidity in capillaries. Gibbs free energy increases, enabling spontaneous chemical reaction to proceed across the cell membrane. Process is altered in the venous blood. Changes in resistance express transformation of the energy in the substance.
Keywords:
Blood Flow Resistance, Blood Viscoelasticity, Gibbs Free Energy, Frequency Dispersion of the Surface Wave, Flow Turbulence

1. Introduction
Consideration of hemodynamics is essential for a comprehensive understanding of the functioning of the circulatory system. Blood flow has a pulsatile distribution in cardiovascular system. Blood vessels and cells are viscoelastic, so classical hydrodynamics and fluids mechanics based on the use of classical viscometers cannot explain hemodynamics. Herewith, it is crucial to take into account a non- Newtonian feature of the blood, which is best studied in rheology and not hydrodynamics [1] .
To investigate blood flow, multidisciplinary study is necessary. Discussion can be made by the law of conservation, as they make it possible to predict the macroscopic behavior of a system without having to consider the microscopic details of the course of a physical process or chemical reaction. Underestimation of the circumstances, leads to the inadequate conclusions, for instance for the flow resistivity.
The resistance offered by the systemic circulation is known as the systemic vascular resistance or total peripheral resistance, offered by the pulmonary circulation―as the pulmonary vascular resistance. In a first approach, based on fluids dy- namics, where the internal friction happens between continuous parallel layers of different velocities, factors that influence vascular resistance are represented in an adapted form of the Hagen-Poiseuille equation and depend on the vessel length, radius and the blood viscosity. In a second approach, more realistic and coming from experimental observations on blood flows, there is a plasma release-cell layering at the walls surrounding a plugged flow. These surrounding layers do not meet at the vessel centre in real blood flow. Instead, there is the plug flow which is hyper viscous because of holding high concentration of red blood cells [2] [3] .
There are many factors that alter the vascular resistance. For the straight direction, blood resistance varies depending on blood viscosity, plugged flow and on the vascular compliance. The effect of the increased resistance of a curved pipe causes diminution of the flux through it. It is found, that this distortion of the velocity profile is accompanied by larger pressure losses along the pipe than that occurs for the same flow with the symmetrical profile which is characteristic of a straight pipe. At very small Reynolds numbers, however, the difference is so slight, but for the ascending aorta Reynolds number, is 10,000; blood flow is turbulent and may contribute to a variety of pathophysiological effects [4] .
The presence of flow separation at arterial branching points and bifurcations is considered to be one of the forms of hydraulic disturbance. Swirling or rotating components of velocity may be induced by rapid turning of the flow direction as arteries bend and branching along their length. With this, flow becomes turbulent with the formation of eddies and chaotic motion which do not contribute to the volume flow rate and increases the resistance dramatically [5] .
Blood flow in large arteries is inertial. Inertia is the resistance of any physical object to change its state of motion; this includes changes to speed, direction or state of rest [6] . It is resistance to the stroke volume in systole.
Due to this, blood flow in human body is full of theoretical and practical controversy. There are lots of factors, which “prevents” the blood flow:
(1) Systolic blood flow in aorta is inertial, with the high Womerslays number.
(2) Blood flow in aortic arch and main pulmonary artery is circular, with the high turbulence and resistivity.
(3) At the arterial branching, flow separation increases flow resistivity.
(4) Increased blood viscosity in the venous blood.
Purpose of the study is to identify the reason for the formation of the resistive factors in the blood flow.
2. Methods and Materials
The velocity of blood flow was studied at the opposite walls of the aortic arch, ascending, thoracic, abdominal aorta and inferior vena cava in 35 normal adult subject (age 21 - 49 year) with the use of Magnetic Resonance Angiography. Be- tween the investigated gender groups (15 men, 20 women), there was no statis- tically evident difference in haemodynamic parameters.
The investigations were done on persons of Caucasian ethnicity. Volunteers had no clinically evident diseases or hemodinamic disorders.
Blood radiodensity (HU) was measured by the CT scanner at the different sites of aorta and inferior vena cava. To avoid densitometric alterations in CT scans, cases were chosen without calcification of the aortic wall, Figure 1.
Blood flow velocity, pulsatility, resistivity indexes were carried out with the Duplex US on the large arteries and inferior vena cava.
3. Results
Peak flow velocity and acceleration in different sites of the aorta made by the Mag- netic Resonance Angiography (MRA) are given in Table 1.
Blood peak systolic velocity (Vps), pulsatility (PI) and resistance indexes (RI) done by Duplex US, Womerlay number (A) of the different vessels are given in Table 2.
Mean velocity, end diastolic velocity and flow acceleration integrated in RI and PI. (RI = (peak systolic velocity − end diastolic velocity)/peak systolic velocity. PI = (peak systolic velocity − end diastolic velocity)/time averaged velocity). Differences in peak flow velocities between the Magnetic Resonance Angiography and Duples US is caused by the place of mesuremen―at the vessel wall and central part of the flow.
Womerslay’s number decreases from the ascending aorta and main pulmona- ry artery, to the peripheral arteries, but increases in large veins. Statistically evident difference (P < 0.05) in the aterial resistive and pulsative indexes is noted from ascending aorta to the internal carotid artery and distal arterial tree. Resistive index in inferior vena cava is low, while Womerlays number is high. Resistive index in pulmonary trunk is lower than that in the ascendant aorta, while Womerslay’s number is higher.
Arterial blood pulsation and flow separation is sharply expressed at the external wall of the aortic arch at the end of systole.
Blood radiodensity in the ascending aorta is 57.3 ± 3.5 HU, distal thoracic aorta 25.7 ± 3.1 HU and in the inferior vena cava 52.3 ± 3.3 HU.
Figure 1. Investigation of the blood radiodensity (HU) in different sites of aorta (decreases distally).
Table 1. Peak flow velocity and acceleration in different sites of the aorta (MRA).
Table 2. Blood flow specifications in largevessels (Duplex US).
4. Discussion
Study of the pulsatile blood flow through the cardiovascular system in precise mathematical terms is insuperable because the blood viscosity is not constant, flow is not steady but pulsatile, vessels are elastic, multi branched conduits with the constantly changing diameter and shape.
Blood, as the cytoplasm and the ground substance in the human body, is thixotropic, non Newtonian fluid [7] . Thixotropy is a time-dependent shear thinning property-becomes thin, less viscous over time, when shaken or otherwise stressed (time dependent viscosity). It is the subject of the energy transmission and can by study by the conservation laws.
Energy can neither be created nor destroyed; rather, it transforms from one form to another. As the arterial blood flow is pulsating, it is reasonable to investigate blood motion as the momentum. Impulse is dimensionally equivalent to the momentum. The momentum of an isolated system is a constant. Momentum can be defined as “mass in motion”. In elastic collision no kinetic energy is lost. Interactions between hard mass spheres may be nearly elastic. Momentum is conserved in inelastic collisions too, but the part of kinetic energy converts to the other forms of energy. In the viscoelastic materials, because of weaker particle interactions, under the high oscillatory pressure, creep and relaxation occur [8] .
When the pulsation of the heart is taken into account, an elastic regime becomes clearly evident [9] . For the human circulatory system, energy transferred to the blood is partially stored in the elastic structure (erythrocyte, arterial wall), another part is dissipated by viscosity, heat and the remaining energy is stored in the kinetic motion of the blood. Blood inflow, can be described as a fluidized suspension of elastic cells, or a sol in constant remodeling form. Structural changes of the blood can be expressed by Womerslays number. Womersley number (A) arises in the solution of the linearized Navier Stokes equations for oscillatory flow (laminar, incompressible) in a tube. It expresses the ratio of the transient inertial force to the sheer force:
Α= √ transient inertial force/viscous force = L√ (ωρ/μ) = L√(ω/ν) [9] .
L is an appropriate length scale (radius of a pipe), ω is the angular frequency of the oscillations, ρ―density, μ―dynamic viscosity, ν―kinematic viscosity of the fluid.
Inertial force is a force that resists the change in velocity of the object due to the mass. Viscous force is an internal friction of the fluids. The dynamic (shear) viscosity of a fluid expresses its resistance to shearing flows, whereas the kinematic viscosity is the ratio of the dynamic viscosity to the density of the fluid. The kinematic viscosity is sometimes referred to as diffusivity of momentum, analogous to diffusivity of heat and mass. When α is small (1 or less, as in capillaries), it means the frequency of pulsations is sufficiently low that a parabolic velocity profile has time to develop during each cycle, and the flow will be very nearly in phase with the pressure gradient and will be given to a good approximation by Poiseuille’s law, using the instantaneous pressure gradient.
Beside this, in capillaries, Fåhræus-Lindqvist effect occurs―huge decreasing of the blood viscosity only if the vessel diameter is between 10 and 300 microme- ters. This is because erythrocytes move over the center of the vessel, leaving plas- ma at the wall of the vessel.
When α is large (10 or more), it means the frequency of pulsations is sufficiently large that the velocity profile is relatively flat (plug flow), and the mean flow lags the pressure gradient by the phase delay.
Some typical values for the Womersley number in different human blood vessels at a heart rate of 2 Hz are: Ascending aorta―13.2, Descending Aorta―11.5; Abdominal Aorta―8; Femoral Artery―3.5; Carotid Artery―4.4; Arterioles― 0.04; Capillaries―0.005; Venules―0.035; Inferior Vena Cava―8.8; Main Pulmo- nary Artery―15 [10] .
Inertiality of the blood at the high Womerslay number represents not only the masses of compounds, but the interaction between them. In classical mechanics, the mass of a system of bodies equals to the sum of the masses of its constituent bodies. In relativistic mechanics the mass of the sum is not a physical quantity, i.e. the mass of the system is generally not equal to the sum of the masses of components and includes the binding energy, which depends on the nature of motion of particles relative to each other. Direct generalization of the concept of mass in hydrostatics and in hydrodynamics, includes such characteristics as the tensor moment of inertia, “body plus environment”, mass displacement―adjoin mass and effective mass.
Greater the mass of the particles, higher the intermolecular attraction in a given volume and they will be less responsive to a disturbance. Materials with very strong particle interactions tend to be more rigid and resistant to deformation. Interaction forces between the particles depend on the distance of action and in cases of the increasing inertiality, density of the substance can be increased. It can be effect of the contraction of long chain in organic substances.
Blood inertiality in the large blood vessels can be revealed by the other way: Variation in volume, thickness and degree of compactness of imaging substances creates a pattern of various densities on the radiograph. In cases of slice constant thickness and volume, increasing of the blood radio density in proximal aorta (51-55HU) indicates increasing in compactness of the blood. It looks like a throm- bus, which has a higher density of 70-90HU, owing to the exclusion of serum from the clot and consequently increased electron density of the coagulum [10] [11] . High radiodensity near the heart can be associated with the erythrocyte aggregation. This phenomenon takes places in normal blood under low-flow conditions or at stasis. Rouleaux are caused by the presence of macromolecules, such as fibrinogen in blood plasma. Fibrinogen is highly elastic. In both, aggregation and coagulation the fibrinogen plays a crucial role. At low shear rates large aggregates lead to an increased viscosity, but by increasing the shear rate, the aggregates break up and the viscosity decreases to a constant high shear rate value.
From the Womerslay’s equation, in the arterial blood flow, if the dynamic viscosity decreases, with the constant density, Womerslay’s number must increase. Womerslay’s number in the distal arteries, with the decreased dynamic viscosity, decreases too. That is why it must be decreasing the effective mass (radiodensity). There are structural changes in the flowing blood, substance with weak particle interactions is easily deformed under pressure and confined to the creeping flow.
Structural alterations in the blood can be explained by the wave propagation at the boundary layer. Human body is hydrocolloid system. In viscoelastic hydrocolloids, due to the wave oscillation, structure of the substance deforms. If the deformation caused by shear stress is elastic, it will return to zero when the force is removed. The remaining deformation i.e. sliding displacement of the chains through the solvent, will not return to zero when the force is removed, forming the flow. Under a constant force the elastic displacement remains constant, whereas the sliding displacement continues. If the force varies sinusoidal with time, the shear strain rate lags behind the changes in the causative force by a phase angle, which is zero for an ideally elastic gel (all energy stored in the material) and 90˚ for an ideally viscous liquid [12] .
Blood during the flow, propagates as the wave. Waves transfer energy and have little or no association with the transportation of mass. Blood flow, near the vessel wall, forms stress-strain interaction of the substance-the surface wave-synergic motion of the longitudinal and phase delayed transversal waves, Figure 2.
In the end of systole arterial pressure drops sharply and the negative pressure propagates distally. Anterograde and retrograde waves undergo interference and at the reflection dissipates aggregates blood cell, while on the vessel wall, pressure shears the endothelial layer and represents the main reason for the atherosclerosis. It is more evident at the end of the arterial flow circle sites [13] [14] .
At the end of the exrental wall of aortic isthmus, amplitude (high flow acceleration due to the increased stress) and oscillation frequency in the reflected wave is higher, than that at the initial part. Due to the frequency dispersion, flow separates [15] , Figure 3.
Damage of the local wall in atherosclerosis can be explained by the wave vector of a plane wave. The wave vector points to the normal direction of the wave surfaces with the constant phase-wave fronts. At the external wall of the isthmus, angle of incidence in the wave vector decreases while the energy transmitted to
Figure 2. Rotation of the surface wave at the boundary. If two perpendicular waves have the same oscillation frequency (ω) and are in phase (φ), than all points the x-value will be same as the y-value, the output will be a straight diagonal line y-x. If the two waves are exactly the same frequency, but out of synch by φ = π/2, than one of the waves will be like a cosine and resultant output will be a circle (or ellipse if the amplitude of signals are different). The appearance of the figure is highly sensitive to the ratio ω1/ω2. For a ratio 2, and phase difference φ = π/2, the Lissajous figure is like-∞. (It looks like a 1S and 2P electron orbital).
Figure 3. Magnetic resonance angiography. Flow quantification. Blood flow at the end of aortic isthmus. Near the external wall, amplitude and frequency of the flow wave oscillation in the reflected wave is higher, than that at the initial, while in the distance from the wall, oscillation frequency is the same (a-d). At the end of systole, pressure drop is coincident with the systolic pressure wave reflection. In aorta Womerslay’s number is high (inertial flow), velocity profile is flat, and flow wave lags behind the pressure wave-there is the phase delay. Due to the wave superposition, pressure at the boundary increases (b). Dashed lines-flow near the external wall (c). Refracted (transmitted) wave in the vessel wall has the same frequency, as the incidental wave. Difference in frequency of the waves, facilitate the structural disaggregation of the flowing mass, separation of the flow and shearing of the vessel wall (d).
the wall increases, Figure 4.
Motion in the circle, forms pressure gradient towards the radius of the rotation and during the wave reflection, it facilitates the flow separation. It’s same for the aortic arch and arterial branching sites. Due to the high turbulence, resistivity in the flow increases and the energy dissipates. Vortices line represents the wave reflection, displaced by the flow. In the arterial blood flow, Womerslay’s number is significantly decreased distal to the high turbulence zones. Turbulence is not chaos, but the method for the distal flow facilitation.
Flow resistance is proportional to the flow velocity, fluid kinematic viscosity, roughness height and inverse proportional to the radius of the vessel (Hagen- Poiseuille equation, Darce friction factor). While, from ascending aorta to the carotids, there is no above mentioned correlation between the resistance index and flow velocity, or the vessel diameter (Table 1) due to changing above mentioned quantities at the flow oscillation.
Pulsatility and resistive indexes are used as pulsed-wave Doppler US measure- ment of downstream renal artery resistance. Resistance of the afferent and efferent arterioles affects both glomerular capillary pressure and the average glomerular capillary plasma formation. Although the functional and structural factors, that contribute to renal blood flow patterns and changes are still not completely understood. Arterial waveform is believed to be the result of both vascular compliance and resistance. Doppler-derived indexes may reflect one or more pathogenetic mechanisms as arterial sclerosis or interstitial fibrosis, which are the main contributors for the vascular distensibility [16] .
Changes in resistivity show structural transformation of the substance with the dissipation of the energy at the time of the wave propagation. High resistance and pressure drop in the arterial blood flow, compared to the venous, shows increased dissipation of the energy. Low resistivity in the inferior vena cava is caused
Figure 4. Wave vector is perpendicular to the wave front. At the external wall of the isthmus, angle of incidence (Φ) of the wave vector decreases and the energy transmitting to the wall increases. Pressure near to the external wall is higher, than that at the internal, while flow velocity is lower. Pressure differences facilitate blood outflow in arterial branches and separation of the flow at the end of the systole.
by the low pressure and high compliance, like in the pulmonary circulation.
Womerslay’s number, more distinctly shows the energy transformation (structural changes of the substance) during the flow, because the effective mass and mass interaction in the environment are changed simultaneously in different ranges and located in opposite to the line fraction (numerator/denominator) in Womerslay’s equation.
Pulsatility and resistivity indexes are decreases from the ascending aorta, to the distal arteries (Table 1). Statistically evident difference (P < 0.001) is noted from ascending aorta to the internal carotid artery and its branches, but not to the abdominal aorta (due to the more low turbulence). Blood pressure and Womersley’s number sharply decreases in the arterioles.
According to the Womersley’s number, changes in the ratio of the transient inertial and viscous forces from the ascending aorta, to the capillaries, changes 2640 times. Travelling time for the erythrocytes from the heart chamber, to the systemic capillaries is about 2 sec. The time is too short for a chemical reaction to take place. Regular changes in Womersley’s number can be caused by the arterial pulse. Blood motion in the heart chambers is inertial (elastic) and the momentum of the system of heart-blood, just at the time of initial systole, becomes near constant. There is increase in efficiency of energy transformation from the contraction of heart muscle, into the energy of blood flow.
Arterial blood flow maintains the process of disorder of complex structures, leading to a global increase in entropy. Sum of the entropy changes in the system and surroundings determines whether a process will occur spontaneously or not. Free energy enables us to express changes, that occur at a constant temperature and pressure (the Gibbs free energy), or constant temperature and volume (the Helmholtz free energy) [17] .
The spontaneous flow of isobaric-isothermal process is determined by two factors: enthalpy―H and entropy―S. The net effect of these opposing factors determines the change in Gibbs free energy ΔG―part of the heat, which can be used to do work in chemical reaction.
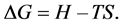
T―Absolute temperature.
The nature of the Gibbs energy change gives an indication of the fundamental possibility of the implementation process. When ΔG < 0, chemical reaction can take place spontaneously, while if ΔG > 0, chemical reaction cannot proceed spontaneously [18] .
Entropy is the measure of the disorder or randomness in a closed system. But from the other hand it is number of microscopic degrees of freedom.
Enthalpy (H = U + PV) includes the internal energy of the matter and amount of energy required to establishing its volume and pressure. It is the energy that is available for conversion into heat at a certain constant pressure.
As the physical dimension, entropy is the amount of transferred energy, divided by the temperature, at which the process takes place. Its essence is easier to understand in melting of an ice: phase-change energy/enthalpy of fusion is the energy that breaks bonds between the molecules in the system (not chemical bonds inside the molecules), does not raise the temperature, but instead enables the molecules to break free to move as liquid―increases entropy. I.e. it is the energy for the structural transformation and cannot be used for work.
There is a close relation between the concepts of entropy and viscosity [19] , associated with systems of conservation laws. That is, the higher the degree of order in the microstructure, the lower the Voronoi entropy and the higher the viscosity [20] . Entropy represents the physical quantity that characterizes the degree of disorder, but regarding architecture of the substance, the entropy is the metaphoric attribute of fluidity.
Entropy usually increases when a liquid or solid dissolves in a solvent. Diffusion of the substances across the cell membrane will give them more space in which to move, with the result that the entropy, of the system is increased. Maximum entropy is achieved when the concentration of molecules is the same on both sides of the membrane.
Enthalpy and entropy are thermodynamic entities and are studied in laws of conservation. Conservation of energy, conservation of momentum persists exact for an isolated system and has far-reaching implications as symmetries of nature.
A particular consequence of the first law of thermodynamics is that the total energy of an isolated system does not change. It can only move from one form to another. On the microscopic scale all interactions are mediated through conservative forces. Energy is never “lost” in the microscopic realm of molecules, atoms, and subatomic particles. Efficiency for the energy transformation is extremely high. Microscopic systems are characterized by conservative forces and reversible processes.
On the macroscopic scale all interactions between systems include no conservative forces. The second law of thermodynamics imposes restrictions on the direction of thermodynamic processes and states that the total entropy of an isolated system always increases over time, shows irreversibility of natural processes and the asymmetry between future and the past. The mechanical energy of macroscopic systems will always dissipated as heat due to the friction/viscosity depending on to efficiency of energy transformation. Macroscopic systems are cha- racterized by no conservative forces and irreversible processes.
During transformation from micro, to macro scale, system becomes more open. In blood flow, as in the living organism overall, interaction between systems on the micro and macro scale persists simultaneously. In the circulatory system chemical energy of glycolysis transforms to the energy of the blood cell and the arterial wall deformation, energy of the blood flow and entropy of the system. Wasting of energy is associated with all processes. It can be reduced, but can ne- ver be eliminated. Cardiac efficiency at the muscle work is normally about 20% - 25%.
Inertial blood flow at the proximal aorta, transforms to viscous one in the capillaries. Structural changes of the blood are expressed in decrease of the Womerlay’s number, dynamic viscosity and radio density. Not only Fåhræus-Lindqvist effect takes part in it. Flow turbulence, due to the anatomical specifications of the arteries, with the frequency dispersion, in the distal arterial tree changes the entropy of the blood. With this, spontaneous reactions in the capillaries across the endothelial cell membrane become more favorable.
Entropy changes not only around the red blood cells, but also within them. When oxygen-hemoglobin complex forms, inside the pumonary capillaries, the oxygen molecule is bound to an iron atom of the hemoglobin molecule―process of combustion. The binding of oxygen by hemoglobin leads to release of heat and increase of entropy in surrounding environment.
From the other hand, low oscillation with the reduced amount of the plasma in the venous blood, decreases entropy of the system and can affect the direction of the chemical processes. In venous blood an aggregation process is connected to the decrease of entropy. With this, In the vicinity of the metabolizing cells, the oxygen-hemoglobin complex breaks up to release oxygen. This is reverse of the oxygen binding reaction by hemoglobin. When it takes place, heat must be supplied from the surrounding environment, with a consequent decrease of entropy [21] .
Entropy difference is the main reason for the positive cooperativity in binding oxygen to hemoglobin and achieved through steric conformational changes of the hemoglobin protein complex [2] .
All the lymph from the lymphatic trunks flows into pulmonary circulation. Herewith, interstitial fluid within the alveoli originates from the pulmonary capillaries. Due to the negative pressure, greatest part is drained by the pulmonary lymphatic drainage and returned to the vascular system. Pulmonary and systemic blood circulations have the same blood flow value, since they are in connected in series. Blood distribution in the pulmonary circulation is about 1/9.3 th of systemic one. Pulmonary vascular resistance is only 1/10th of its systemic counterpart. Recirculation in the pulmonary interstitial fluid must be 9.3 times higher, than that in systemic, Figure 5. Entropy can be increased in the pulmonary capi- llaries and facilitate cooperativity.
High entropy of lymphatic system affects the initial route by which tumors and infectious agents spread [22] , it determines the importance of lymph flow for the lipid absorption [23] and the spontaneity of the process.
Due to the all above mentioned, the main goal for the blood thixotropy and erythrocyte aggregation, is the energy distribution in the body, by the help of the arterial pulse.
5. Conclusion
Heart energy is stored in the elastic deformation of the blood cells and arterial walls, in kinetic energy of the blood flow, entropy of the system. Elasticity of the structure is conjunct with the effective mass of the system. Inertial blood flow due to the frequency dispersion in the arteries, transforms to the flow with the high fluidity in capillaries. Gibbs free energy increases, enabling spontaneous chemical reaction to proceed across the cell membrane. Process is altered in the
Figure 5. (a) Systemic and pulmonary blood circulation. (b) Circulation of blood and lymph. At the entrance of the right atrium, lymph mixes with the venous blood and after the systolic oscillation; it flows to the pulmonary circulation. From the lung alveolus, oxygen dissolves in interstitial space and is absorbed by the red blood cells in capillary network around the alveolus. Oxygen initially dissolved in the blood serum, reacts with hemoglobin to form oxygen-hemoglobin complex. Blood volume of the systemic circulation normally 9.3 times higher, than that the pulmonary circulation. Pulmonary and systemic blood circulations have the same blood flow value, since they are connected in series. Angular frequency of the pulmonary lymph circulation must be 9.3 higher than that in systemic.
venous blood. Changes in resistance express transformation of the energy in the substance at the time of the wave propagation.
Cite this paper
Beraia, G. and Beraia, M. (2017) Resistive Factors of the Blood Flow and Energy Distribution in the Body. Health, 9, 459-472. https://doi.org/10.4236/health.2017.93033
References
- 1. Secomb, T.W. (2016) Hemodynamics. Comprehensive Physiology, 6, 975-1003.
- 2. Hall, J.E. (2015) Guyton and Hall Textbook of Medical Physiology. Elsevier, Amsterdam, 13e.
- 3. Galdi, G.P., Rannacher, R., Robertson, A.M. and Turek, S. (2008) Hemodinamical Flows: Modeling, Analysis, and Simulation. Birkhäuser, Basel.
- 4. Wang, C.Y. and Bassingthwaighte, J.B. (2014) Blood Flow in Small Curved Tubes. Journal of Biomechanical Engineering, 125, 910-913.
- 5. White, F.M. (2016) Fluid Mechanics. McGraw Education, New York.
- 6. Halliday, D., Resnick, R. and Walker, J. (2011) Fundamentals of Physics. John Wiley & Sons, Hoboken.
- 7. Thurston, G.B. (1972) Viscoelasticity of Human Blood. Biophysical Journal, 12, 1205-1217.
https://doi.org/10.1016/S0006-3495(72)86156-3 - 8. Tanner, R.I. (2000) Engineering Rheology. Oxford University Press, Oxford.
- 9. Fung, Y.C. (1984) Biomechanics Circulation. Springer, Berlin.
- 10. New, P.F. and Aronow, S. (1976) Attenuation Measurements of Whole Blood and Blood Fractiones in Computed Tomography. Radiology, 121, 635-640.
https://doi.org/10.1148/121.3.635 - 11. Wittram, C., Maher, M.M. and Halpern, E.F.S. (2005) Attenuation of Acute and Chronic Pulmonary Emboli. Radiology, 235, 1050-1054.
- 12. Lakes, R.S. (2009) Viscoelastic Materials. Cambridge University Press, Cambridge.
https://doi.org/10.1017/CBO9780511626722 - 13. Wilmer, N.W., Michael, F.O. and Charalambos, V.M.D. (2011) McDonald’s Blood Flow in Arteries: Theoretical, Experimental and Clinical Principles. CRC Press, Boca Raton, 755.
- 14. Cunningham, K.S. (2005) The Role of Shear Stress in the Pathogenesis of Atherosclerosis. Laboratory Investigation, 85, 942.
- 15. Merab, B. and Guram, B. (2015) Frequency Dispersion on the Vessel Wall—Primary Reason of Atherosclerosis. 5th International Conference on Clinical & Experimental Cardiology, Philadelphia, 27-29 April 2015, 145.
- 16. Viazzi, F., Leoncini, G., Derchi, L.E. and Pontremoli, R. (2014) Ultrasound Doppler Renal Resistive Index: A Useful Tool for the Management of the Hypertensive Patient. Journal of Hypertension, 32, 149-153.
https://doi.org/10.1097/HJH.0b013e328365b29c - 17. Ball, D.W. (2015) Physical Chemistry. Stanford University, Stanford.
- 18. Atkins, P. and De Paula, J. (2014) Atkins’ Physical Chemistry. Oxford University Press, Oxford.
- 19. Tadmor, E. (1984) Numerical Viscosity and the Entropy Condition for Conservative Difference Schemes. Mathematics of Computation, 43, 369-381.
https://doi.org/10.1090/S0025-5718-1984-0758189-X - 20. Gao, W., Feng, S.-D., Zhang, S.-L., Qi, L. amd Liu, R.-P. (2015) Relationship between Voronoi Entropy and the Viscosity of Zr36Cu64 Alloy Melt Based on Molecular Dynamics. Chinese Physics B, 24, Article ID: 126102.
- 21. Goldshtein, M. and Goldshtein, I.F. (1995) The Refrigerator and the Universe. Understanding the Laws of Energy. Harvard University Press. Cambridge, London.
- 22. Wong, S.Y. and Hynes, R.O. (2006) Lymphatic or Hematogenous Dissemination: How Does a Metastatic Tumor Cell Decide? Cell Cycle, 5, 812-817.
https://doi.org/10.4161/cc.5.8.2646 - 23. Dixon, J.B. and Ann, N.Y. (2010) Mechanisms of Chylomicron Uptake into Lacteals. Annals of the New York Academy of Sciences, 1207, E52-E57.







