Health
Vol.07 No.06(2015), Article ID:57213,10 pages
10.4236/health.2015.76084
Implementation and Validation of a Stride Length Estimation Algorithm, Using a Single Basic Inertial Sensor on Healthy Subjects and Patients Suffering from Parkinson’s Disease
Benoît Sijobert1, Mourad Benoussaad1, Jennifer Denys1, Roger Pissard-Gibollet2, Christian Geny3, Christine Azevedo Coste1
1DEMAR, INRIA-LIRMM, Montpellier, France
2INRIA, Montbonnot, France
3Neurological Department, CHU Gui de Chauliac, Montpellier, France
Email: benoit.sijobert@inria.fr
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 1 May 2015; accepted 13 June 2015; published 17 June 2015
ABSTRACT
As low cost and highly portable sensors, inertial measurements units (IMU) have become increasingly used in gait analysis, embodying an efficient alternative to motion capture systems. Meanwhile, being able to compute reliably accurate spatial gait parameters using few sensors remains a relatively complex problematic. Providing a clinical oriented solution, our study presents a gyrometer and accelerometer based algorithm for stride length estimation. Compared to most of the numerous existing works where only an averaged stride length is computed from several IMU, or where the use of the magnetometer is incompatible with everyday use, our challenge here has been to extract each individual stride length in an easy-to-use algorithm requiring only one inertial sensor attached to the subject shank. Our results were validated on healthy subjects and patients suffering from Parkinson’s disease (PD). Estimated stride lengths were compared to GAITRite© walkway system data: the mean error over all the strides was less than 6% for healthy group and 10.3% for PD group. This method provides a reliable portable solution for monitoring the instantaneous stride length and opens the way to promising applications.
Keywords:
Inertial Measurement Unit (IMU), Stride Length, Gait Analysis, Parkinson’s Disease, Biologging

1. Introduction
Tracking and analyzing a pathological movement is a recurrent need for clinical assessment. Camera-based motion capture, well known as a present gold standard, enables practitioners and scientists to perform such observations with a high accuracy. Meanwhile, due to a hampering lack of mobility in addition to a significant financial cost, this technology trends to be unusable in certain contexts, such as an embedded or outdoor use. In those cases, inertial measurement units embody an efficient alternative for movement analysis, such as in sport competition or gait disorders contexts [1] [2] . Quantitative assessment of Parkinson’s disease (PD)-associated signs and disability using wearable technology is also knowing a rapidly growing interest [3] .
Among multiple gait parameters, stride length is frequently observed for rehabilitation and diagnostic purposes. Applied to neurological diseases, it represents an extremely helpful marker for practitioners to analyze pathological effects on gait and therapy efficiency. Preliminary work showed that monitoring the instantaneous stride length gave a crucial information to online detect or anticipate freezing of gait (FOG, an episodic inability to generate effective stepping) in patients suffering from Parkinson’s disease [4] [5] . Measuring the physical activity of those patients and quantifying FOG events could also enable to differentiate “OFF” times, a state of decreased mobility associated to a low L-dopa level, and “ON” times, or periods when the medication is working and symptoms are controlled [6] .
Numerous works showed the complexity and the diversity of accurately analyzing gait parameters in clinical applications, using wearable and non-wearable systems [7] . Most of the existing works on IMU-based stride length estimation only provide an average stride length (ex: RehaWatch© device). Usually based on the estimation of the distance covered in a fixed time interval, the stride is computed from the whole recording trial [8] . Other works performed stride length calculation with at least two IMUs [9] [10] , or using motion pattern identification [11] , thereby requiring a prior knowledge of the subject's biomechanical model and increasing installation time.
Keeping in mind our objective of conceiving a light and noninvasive patient oriented solution, quickly implementable and easy to put ON and OFF, our objective here is to demonstrate the feasibility of computing each single stride length from a maximum of one IMU per leg. Only two accurate enough (<10%) solutions based on one IMU without using magnetometer values are available in the literature. The study of Köse et al. [12] is able to provide the instantaneous stride length calculated from an inertial sensor located on the pelvis. Meanwhile, due to an algorithm based on acceleration patterns identification and pelvis displacement estimation, the authors exposed some limitations regarding pathological gait. The second one is the solution proposed by Mariani et al. [13] , which presents a 3D gait assessment method validated on both young and elderly valid subjects. Using a foot-worn inertial sensor, it uses a complex de-drifting method based on sigmoid-like curve substraction modeled from a p-chip interpolation function (Carlson and Fritsch, 1985).
Therefore, despite of their ease-of-use, robust design, low-cost, and their small dimensions, numerous well known issues make the IMU exploitation relatively complex and hardly usable for a medical practitioner. Indeed, partly due to the high drift of the inertial data after numerical integration, limbs position and orientation in space cannot be simply obtained by integrating accelerations and angular velocities recorded by means of accelerometers and rate gyrometers.
Through this paper, we propose a simple clinical use designed solution for calculating each stride length, using only one basic shank-located IMU, validated from GAITRite© electronic walkway measurements [14] [15] on both healthy and PD subjects.
2. Method
2.1. Algorithm Development
The algorithm presented in this study uses data from one 3D gyrometer and one 3D accelerometer embedded in an inertial measurement unit (IMU) strapped to the leg. As previously explained, it does not use any magnetometer data. The acquisition frequencies were 200 Hz for both sensors.
2.1.1. Calibration
Calibration of the IMU used in our experiments has turned to be critical and was the primary task to achieve an efficient algorithm. The accelerometers were calibrated using the physical property that the modulus of the acceleration, in static conditions, is equal to gravity acceleration g:
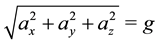 (1)
(1)
We placed the IMU sensor in different random orientations. For each orientation, we recorded the sensor output while maintaining it in a strictly static state. We tried different existing calibration algorithms and we had the best performances using the Frosio et al. calibration model [16] . It has the advantages of incorporating not only the bias and scale factor for each axis but also the cross-axis symmetrical actors computed through Gauss- Newton nonlinear optimization.
Regarding the gyrometer calibration, each recording session started by a motionless period where the angular velocity is supposed to be zero. The post-processing algorithm automatically detected this moment and compensated an eventual existing offset.
2.1.2. Filtering
Both accelerometer and gyrometer measurements have been filtered with a forward-backward lowpass Butterworth filter (order 1, Fcutoff = 5 Hz). In order to reduce the integration drift, partially due to a continuous component, we performed also a forward-backward highpass Butterworth filtering (order 1, Fcutoff = 0.001 Hz) on the gyrometer data.
2.1.3. Segmentation
Firstly, the continuous walking motion had to be segmented into a series of stride cycles to compute the horizontal movement for each stride. We chose to use the gyrometer signal for determining the shank vertical event (time in the stance phase when the shank is parallel to the direction of gravity) thereby bounding each cycle. A simple automatized detection of this characteristic feature in the angular velocity was performed as shown in Figure 1.
2.1.4. Stride Length
The principle of stride length estimation is to calculate the horizontal movement of the inertial sensor during one stride cycle (Figure 2) in the sagittal plane. We started from the algorithm originally proposed by Li et al. [17]
Figure 1. Angular velocity (indeg/s) of the shank during sevens trides. We use this gyrometer signal for segmenting the gait into strides. The characteristic features of swing and stance events enable to detect the mid-stance shank vertical event (start/stop events).
Figure 2. Frame schema: the IMU is located on the shank side, in sagittal plane. The angular velocity ω is clock wise positive. D is the distance between the sensor and the ankle joint (malleolus) and θ is the sensor orientation.
and improved later by Laudanski et al. [18] which computes the walking speed from a shank-mounted IMU. We adapted it for calculating the stride length, by correcting and integrating the linear velocity along the stride duration, thereby obtaining the length of each stride. As only the horizontal velocity was needed, we also simplified it. As an effort to provide an easy-to-implement solution, we made the hypothesis that the sensor is initially set in the sagittal plane and does not move during the experiment, thereby working in a 2D frame. Most of all, we implemented it with optimized raw data conditioning (sampling rate, filtering and calibration) and integration methods (see Discussion part) which it turned to be critical steps. To begin, the sensor orientation θ(t) has to be computed by integrating the measured angular velocity ω(t) on as tride cycle (from t = 0 to t = tend, the initialtilt at the beginning of the cycle θ(0) = 0, assuming the sensoris aligned to the limb):
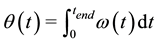 (2)
(2)
The horizontal component acceleration a hor(t) in the world coordinate system has to be calculated from the measured raw accelerations, ay(t) and ax(t):
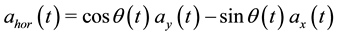 (3)
(3)
The integration of the horizontal acceleration provides the horizontal velocity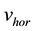 :
:
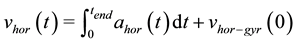 (4)
(4)
where 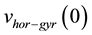 is the initial horizontal speed computed from gyrometer data at the start of the cycle:
is the initial horizontal speed computed from gyrometer data at the start of the cycle:
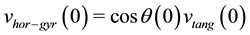 (5)
(5)
with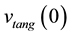 :
:
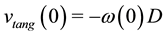 (6)
(6)
and 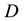 the distance between the IMU and the ankle joint.
the distance between the IMU and the ankle joint.
A velocity drift correction is then performed at the end of each cycle. The linear trend difference between the calculated velocity vhor(tend) and the gyrometer based velocity vhor-gyr(tend) at the stride end is added:
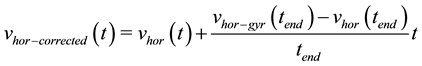 (7)
(7)
Once the 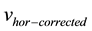 computed, a simple trapezoidal integration provides the horizontal displacement during a stride cycle:
computed, a simple trapezoidal integration provides the horizontal displacement during a stride cycle:
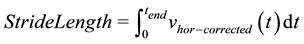 (8)
(8)
2.2. Experimental Protocol
10 healthy subjects, (5 male, 5 female; Age range: 23 to 61 years; Height range: 1.55 to 1.89 m) and 12 patients suffering from Parkinson’s disease (9 male, 3 female; Age range: 63 to 82 years) participated to the study. The protocol has been approved by the local ethical committee (international identification number NCT02317289). Patients were recruited at the Neurology (Chauliac Hospital) and Gerontology (Balmes Center) departments of Montpellier hospital (CHU Montpellier). The participants provided their written informed consent. Subjects walked continuously for approximately 7 m along the GAITRite© electronic walkway (spatial accuracy ±0.0127 m, CIR Systems, Inc., Havertown, PA, USA) with two HikoB Fox© (HikoB© Villeurbanne, France) inertial measurement units respectively strapped to the foot and the shank of each leg, as illustrated in Figure 3. The distance D between the IMU and the ankle joint was systematically measured once the subject equipped. Each subject from the healthy group performed two iterations of the walk at self-selected walking speeds (‘normal’ and “fast”). Subjects from PD group only walked at their comfort speed. The IMU were remotely controlled and synchronized each other via a radio beacon. The GAITRite device provided a +5V trigger output for synchronizing data acquisition with the HikoB inertial sensors, enabling to include all the strides of each gait sequence. Based on each single IMU, individual stride lengths were estimated from the previously explained algorithm and compared one by one to the stride lengths provided by the GAITRite software. For each of the two sensors located on each leg, we observed the influence of the IMU location (shank or foot mounted), the walking speed, the sampling rate and the filtering on the mean and maximum stride length calculation error.
3. Results
For each subject in the two groups (Healthy/PD), data from inertial sensors were automatically segmented into stride cycles and the length of each stride was estimated. Each estimated stride length was compared to the corresponding stride length value in GAITRite (Figure 4). For each subject and for each of the 4 IMUs (shank and foot on each leg), we calculated the mean error and the standard deviation between considered IMU-based stride length estimation and corresponding stride length extracted from GAITRite (Table 1 and Table 2).

Figure 3. Inertial measurement units (HikoBFox©) (a) were strapped to the foot and the shank of each leg (b). The distance D between the IMU and the ankle joint was system atically measured.
Figure 4. Estimation error (in cm) of the stride length between GAITRite data (blue line) and IMU-based estimation (green line) for each of the 9 strides of the considered trial.
Table 1. Experiments results: healthy subjects.
Table 2. Experiments results: Parkinson’s disease patients.
3.1. Healthy Subjects
399 strides (229 in comfort walking, 170 in fast walking) were computed and compared one by one to the GAITRite results. For each subject and for each of the 4 IMUs (shank and foot on each leg), we calculated the mean error and the standard deviation between considered IMU-based stride length estimation and corresponding stride length extracted from GAITRite (Table 3).
For the shank mounted IMUs, we obtained a mean error of 5.9% for the “normal” walk and 5.4% for the “fast” one. Standard deviation is also low, less than 10 cm in average. We observed a slight difference between the foot and the shank location (the results are 3.2% better for shank mounted IMU).
As we can observe in Figure 5, stride lengths are very variable over the subjects. We recorded ’normal’ strides going from 113 to 173 cm and from 140 to 200 cm for the “fast” ones. Despite a huge speed increase between the two types of walks in some subjects (ex: subject 4, from 116 to 243 cm/s), the mean error remains under 10% in worst cases with a mean error of 5.6% (0.09 m) on both “fast” and “normal” walk using the shank mounted IMUs.
3.2. PD Subjects
In the Parkinson’s Disease group, despite of consequently smaller and slower strides, we obtained a mean error of 9.5% for both legs using the shank mounted IMUs (Table 2) (8.6% for the left leg, and 10.3% for the right one). Standard deviation is also low, less than 5 cm in average.
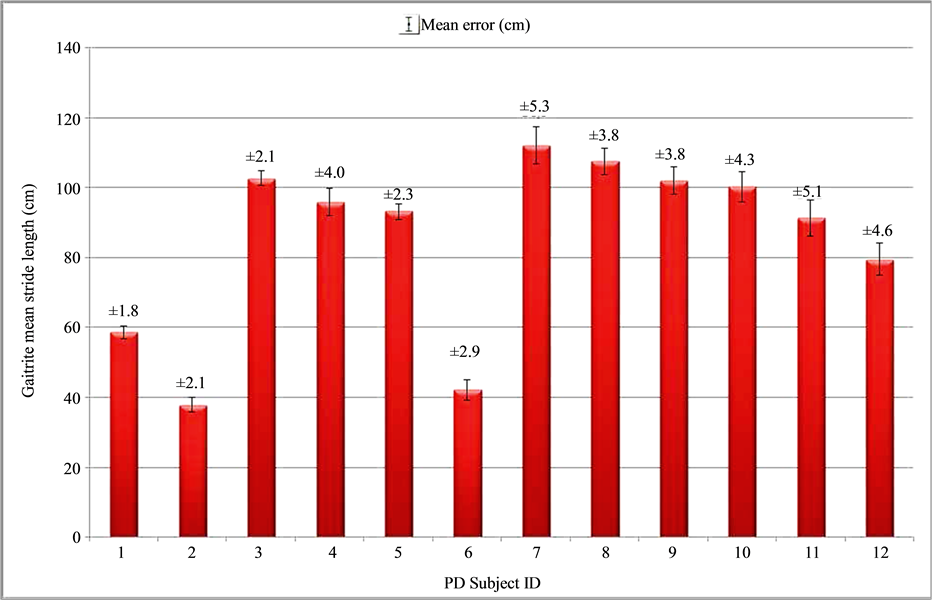
As we can observe in Figure 6, stride lengths are variable over the subjects. We recorded strides going from 38 to 113 cm. In the worst case (subject 11) the mean error is 11.2% (0.102 m).
4. Discussion & Conclusions
The proposed stride length calculation algorithm has been validated using the GAITRite system. The results emphasized the reliability of our algorithm in the gait analysis of healthy volunteers, with variable lengths (113 to 200 cm) and speeds (79 to 244 cm/s) but also on patients suffering from Parkinson’s disease, with consistently smaller stride lengths (38 to 113 cm). Despite of using only one sensor by leg, we showed that gait segmentation and stride length estimation were accurate and robust enough to fit different morphology and type of gait
Table 3. Patients characteristics.
Figure 5. Stride length results on 10 Healthy subjects based on the left shank IMU data. The bars represents the real length measured by the GAITRite, above that the calculated mean error between IMU-based estimation and GAITRite measurement is presented in cm.
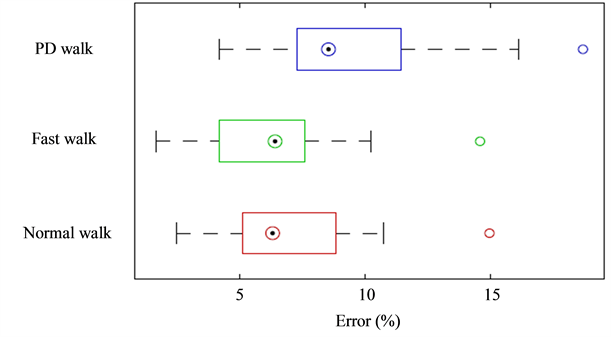
patterns, with a mean error less than 9%. Figure 7 shows a similar median error between fast and normal walk. We claim to provide a solution able to calculate the stride length without a complex prior knowledge of the biomechanical model. The distance between the sensor and the ankle joint has been systematically measured during the experiments and has been taken into account in the algorithm. Meanwhile, we observed that the accuracy of this measure has a neglectable impact on the performance of the results and can be approximately (±2
Figure 6. Stride length results on 12 patients suffering from Parkinson’s disease based on the left shank IMU data. The bars represents the real length measured by the GAITRite, above that the calculated mean error between IMU-based estimation and GAITRite measurement is presented in cm.
Figure 7. Box plots presenting all the errors (%) between all the trials and subjects, from both shank IMUs, for valid and Parkinson’s disease gait.
cm) provided by the user. We tried two different sensors location, the results showed that the error was slightly increased (~3%) for the foot mounted IMU. Indeed, at the mid-stance shank vertical event, the angular velocity reached a local maximum. At faster walking speeds, the impact of this estimated initial velocity based on the angular velocity becomes more important on the accuracy of the stride. Because the shank IMU has a greater angular velocity than the foot one, the speed estimation algorithm slightly underestimates it. For some isolated cases, we had an important maximum error (~30 cm) generally due to a bad stride cycle detection (the vertical shank event is not properly detected because the gait pattern is too distorted). We observed in most of the cases that PD gait presents a pattern similar to healthy gait. Nevertheless, some patients showed huge difficulties to walk (outlier in Figure 7), thereby creating a hardly automatically and reliably segmentable pattern, which does not look as a step anymore. In these cases, the identification pattern used by [13] is likely to be unusable. This underlines the influence of the segmentation process on the results, which is the most sensitive part of the algorithm. In future works, the segmentation could be improved by also using the accelerometer values for detecting the shank verticality [19] or by combining our segmentation algorithm to AHRS(Attitude and Heading Reference System) algorithms for estimating the exact sensor orientation [20] [21] . We could also add a second IMU on the opposite leg and use the swing phase of one leg for robustly detecting the stance phase of the other [10] .
The raw signals filtering also turned to be critical. Compared to other studies where a simple high pass filtering of the raw values is performed, we found essential here to perform it in a zero-phase filtering way for keeping a zero-phase distortion between accelerometer and gyrometer values.
We also tried three different numerical integration methods for improving our results, the strap-down, the Simpson’s and the trapezoidal ones. We found the strap-down rule induced less drift, but the best time-con- suming/efficiency ratio was obtained with the classical trapezoidal rule. Indeed, as we only integrated the signals on a stride duration, the numerical drift due to the trapezoidal rule was not significant.
We designed a reliable portable solution by making the choice to develop an algorithm without using the built-in IMU magnetometer sensor. By providing a non-sensitive magnetic field variation solution, we improved the reliability of our algorithm for different everyday life situations. Still related to portability issues, we also chose to implement a generic solution which is basically usable with any inertial sensor [22] .
Different applications could be consequently considered using this algorithm. In this paper we presented an offline processing, but we will need to make it evolve towards a real time calculation process for our future works, i.e. gait assistive devices. For instance, in order to pilot an auditory system based on freezing events detection for Parkinson’s disease [23] .
All of these research topics show a common need to easily and robustly export the instantaneous stride length for different types of gaits and contexts. In our next experiments, we will have to face numerous issues due to online processing, such as the filtering delay, the real time segmentation (in the current state, the algorithm would have a one stride delay because the current gait cycle has to be ended for being segmented) or the hardware limited real-time sampling rate (below 100 Hz we found an undersampled acceleration signal causes major deterioration of the results).
Acknowledgements
This work was supported by an INRIA internal financial support: ADT SENSBIO and a Montpellier Hospital internal financial support (AOI PARKDEMAR CHU Montpellier).
References
- Chelius, G., Braillon, C., Pasquier, M., Horvais, N., Gibollet, R.P., Espiau, B. and Coste, C.A. (2011) A Wearable Sensor Network for Gait Analysis: A Six-Day Experiment of Running through the Desert. IEEE/ASME Transactions on Mechatronics, 16, 878-883. http://dx.doi.org/10.1109/TMECH.2011.2161324
- Azevedo Coste, C., Jović, J., Pissard-Gibollet, R. and Froger, J. (2014) Continuous Gait Cycle Index Estimation for Electrical Stimulation Assisted Foot Drop Correction. Journal of NeuroEngineering and Rehabilitation, 11. http://dx.doi.org/10.1186/1743-0003-11-118
- Maetzler, W., Domingos, J., Srulijes, K., Ferreira, J.J. and Bloem, B.R. (2013) Quantitative Wearable Sensors for Objective Assessment of Parkinson’s Disease. Movement Disorders: Official Journal of the Movement Disorder Society, 28, 1628-1637. http://www.ncbi.nlm.nih.gov/pubmed/24030855
- Azevedo Coste, C., Sijobert, B., Pissard-Gibollet, R., Pasquier, M., Espiau, B. and Geny, C. (2014) Detection of Freezing of Gait in Parkinson Disease: Preliminary Results. Sensors, 14, 6819-6827. http://dx.doi.org/10.3390/s140406819
- Djuric Jovicic, M., Jovicic, N., Radovanovic, S., Stankovic, I., Popovic, M. and Kostic, V. (2013) Automatic Identification and Classification of Freezing of Gait Episodes in Parkinson’s Disease Patients. IEEE Transactions on Neural Systems and Rehabilitation Engineering: A Publication of the IEEE Engineering in Medicine and Biology Society. http://www.ncbi.nlm.nih.gov/pubmed/24235277
- Cancela, J., Pastorino, M., Arredondo, M.T., Nikita, K.S., Villagra, F. and Pastor, M.A. (2013) Feasibility Study of a Wearable System Based on a Wireless Body Area Network for Gait Assessment in Parkinson’s Disease Patients. Sensors (Basel, Switzerland), 14, 4618-4633. http://www.pubmedcentral.nih.gov/articlerender.fcgi?artid=4003960 http://dx.doi.org/10.3390/s140304618
- Murodela Herran, A., Garcia-Zapirain, B. and Mendez-Zorrilla, A. (2014) Gait Analysis Methods: An Overview of Wearable and Non-Wearable Systems, Highlighting Clinical Applications. Sensors, 3362-3394. http://dx.doi.org/10.3390/s140203362
- Yang, S. and Li, Q. (2012) Inertial Sensor-Based Methods in Walking Speed Estimation: A Systematic Review. Sensors, 12, 6102-6116. http://dx.doi.org/10.3390/s120506102
- Aminian, K., Najafi, B., Leyvraz, P.F. and Robert, P. (2002) Spatio-Temporal Parameters of Gait Measured by an Ambulatory System Using Miniature Gyroscopes. Journal of Biomechanics, 35, 689-699. http://dx.doi.org/10.1016/S0021-9290(02)00008-8
- Trojaniello, D., Cereatti, A., Pelosin, E., Avanzino, L., Mirelman, A., Hausdorff, J.M. and Croce, U.D. (2014) Estimation of Step-by-Step Spatio-Temporal Parameters of Normal and Impaired Gait Using Shank-Mounted Magneto-Iner- tial Sensors: Application to Elderly, Hemiparetic, Parkinsonian and Choreicgait. Journal of Neuroengineering and Rehabilitation, 1-12.
- Rampp, A., Barth, J., Schulein, S., Gasmann, K., Klucken, J. and Eskofier, B. (2015) Inertial Sensor-Based Stride Parameter Calculation From Gait Sequences in Geriatric Patients. IEEE Transactions on Biomedical Engineering, 62, 1089-1097. http://dx.doi.org/10.1109/TBME.2014.2368211
- Köse, A., Cereatti, A. and Croce, U.D. (2012) Bilateral Step Length Estimation Using a Single Inertial Measurement Unit Attached to the Pelvis. Journal of NeuroEngineering and Rehabilitation, 9, 9. http://dx.doi.org/10.1186/1743-0003-9-9
- Mariani, B., Hoskovec, C., Rochat, S., Büla, C., Penders, J. and Aminian, K. (2010) 3D Gait Assessment in Young and Elderly Subjects Using Foot-Worn Inertial Sensors. Journal of Biomechanics, 43, 2999-3006. http://www.sciencedirect.com/science/article/pii/S0021929010003684 http://dx.doi.org/10.1016/j.jbiomech.2010.07.003
- Webster, K.E., Wittwer, J.E. and Feller, J.A. (2005) Validity of the Gait Rite Walkway System for the Measurement of Averaged and Individual Step Parameters of Gait. Gait and Posture, 22, 317-321. http://www.sciencedirect.com/science/article/pii/S0966636204002061 http://dx.doi.org/10.1016/j.gaitpost.2004.10.005
- Nelson, A.J., Zwick, D., Brody, S., Doran, C., Pulver, L., Rooz, G., Sadownick, M., Nelson, R. and Rothman, J. (2002) The Validity of the Gait Rite and the Functional Ambulation Performance Scoring System in the Analysis of Parkinson Gait. Neuro Rehabilitation, 17, 255-262. http://iospress.metapress.com/content/KVTKPTU0PPWFWU8A
- Frosio, I., Pedersini, F., Borghese, N.A. and Model, A.S. (2009) Auto Calibration of MEMS Accelerometers. IEEE Transactions on Instrumentation and Measurement, 58, 2034-2041. http://dx.doi.org/10.1109/TIM.2008.2006137
- Li, Q., Young, M., Naing, V. and Donelan, J.M. (2010) Walking Speed Estimation Using a Shank-Mounted Inertial Measurement Unit. Journal of Biomechanics, 43, 1640-1643. http://dx.doi.org/10.1016/j.jbiomech.2010.01.031
- Laudanski, A., Yang, S. and Li, Q. (2011) A Concurrent Comparison of Inertia Sensor-Based Walking Speed Estimation Methods. Proceedings of the 2011 Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Boston, 30 August-3 September 2011, 3484-3487. http://dx.doi.org/10.1109/IEMBS.2011.6090941
- Moore, S.T., MacDougall, H.G., Gracies, J.M., Cohen, H.S. and Ondo, W.G. (2007) Long-Term Monitoring of Gait in Parkinson’s Disease. Gait and Posture, 26, 200-207. http://www.ncbi.nlm.nih.gov/pubmed/17046261 http://dx.doi.org/10.1016/j.gaitpost.2006.09.011
- Martinand, P. and Salau¨n, E. (2010) Design and Implementation of a Low-Cost Observer-Based Attitude and Heading Reference System. Control Engineering Practice, 18, 712-722. http://dx.doi.org/10.1016/j.conengprac.2010.01.012
- Madgwick, S.O.H., Harrison, A.J.L. and Vaidyanathan, R. (2011) Estimation of IMU and MARG Orientation Using a Gradient Descent Algorithm. Proceedings of the 2011 IEEE International Conference on Rehabilitation Robotics, Zurich, 29 June-1 July 2011, 1-7. http://dx.doi.org/10.1109/ICORR.2011.5975346
- Sijobert, B., Gibollet, R.P., Azevedo, C. and Sensbio, T.K. (2015) An Open-Source Generic Toolkit for Inertial Sensors Based Motion Analysis. https://github.com/sensbio/sensbiotk
- Sijobert, B., Azevedo, C., Denys, J. and Geny, C. (2014) IMU Based Detection of Freezing of Gait and Festination in Parkinson’s Disease. Proceedings of the 19th International Functional Electrical Stimulation Society (IFESS) Annual Conference, Kuala Lumpur, 17-19 September 2014, 1-3. http://dx.doi.org/10.1109/ifess.2014.7036751