Health Vol.07 No.02(2015), Article ID:54111,10 pages
10.4236/health.2015.72026
Dose Reduction by the Use of a Wavelet-Based Denoising Method for Digital Radiography
Haruyuki Watanabe1, Du-Yih Tsai2, Yongbum Lee2, Eri Matsuyama3
1School of Radiological Technology, Gunma Prefectural College of Health Sciences, Gunma, Japan
2Department of Radiological Technology, Graduate School of Health Sciences, Niigata University, Niigata, Japan
3Department of Radiological Technology, Faculty of Fukuoka Medical Technology, Teikyo University, Fukuoka, Japan
Email: hal-watanabe@gchs.ac.jp
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 31 December 2014; accepted 10 February 2015; published 15 February 2015
ABSTRACT
The primary purpose of this paper is to provide a novel wavelet-domain method for digital radiography with low dose examination. Approach of this study is an improved wavelet-transform- based method for potentially reducing radiation dose while maintaining clinically acceptable image quality. The wavelet algorithm integrates the advantages of wavelet-coefficient-weighted method and the existing Bayes Shrink thresholding method. In order to confirm the usefulness of the proposed method, the resolving and noise characteristics of the processed computed radiography images were measured. In addition, variations of contrast and noise with respect to radiation dose were also examined. Finally, to verify the effect of clinical examination, visual evaluations were also performed in lower abdominal area using phantom. Our quantitative results demonstrated that our wavelet algorithm could improve resolution characteristics while keeping the noise level within acceptable limits. Visual evaluation result demonstrated that the proposed method was superior to other published methods. Our proposed method recognized effect on decreasing in exposure dose in lower abdominal radiographs. As a conclusion, our proposed method’s performance is better when compared with that of the 3 conventional methods. The proposed method has the potential to improve visibility in radiographs when a lower radiation dose is applied.
Keywords:
Radiation Dose, Image Quality, Image Processing, Noise Reduction, Wavelet Transforms

1. Introduction
The issue of radiation dose exposure to patients from digital radiography is a major public health concern. In particular, it is important to keep radiation dose exposure to a minimum in female patients during their reproductive period, who frequently undergo repeated radiation exposure during the course of diagnostic imaging and treatment follow-up.
It is known that a trade-off exists between noise level and radiation dose. On the one hand, high-dose radiation will lower the noise level, but may expose the patient to excessive radiation. On the other hand, low-dose radiation will lower the signal-to-noise ratio of the image and result in reducing the amount of image information. The balancing of radiation dose and image quality should be performed precisely to ensure that patient doses are kept at a reasonable minimum, while maintaining clinically acceptable image quality. To address this issue, much research, including the development of new detectors and image processing methods [1] -[3] has been carried out. In recent years, several investigators have reported that wavelet-based image processing techniques are effective in the reduction of radiation dose [4] -[13] .
Conventional radiography is widely used for the pelvis and lumbar spine. However, the radiation dose for pelvic and lumbar x-ray examinations using a radiograph is relatively high in order to obtain acceptable image quality. An effort to reduce the exposure dose can have a positive effect on a patient’s quality of life.
In this study, we propose an improved wavelet-transform-based method for potentially reducing the radiation dose while maintaining clinically acceptable image quality. The proposed method integrates the advantages of our previously proposed wavelet-coefficient-weighted method [11] -[13] and the existing Bayes Shrink thresholding method [14] . The wavelet-coefficient-weighted method has the advantage of effective edge enhancement accompanied by a slight suppression of noise increase (however, the noise is also enhanced definitely). In contrast, the Bayes Shrink thresholding method [14] is used for denoising, while the edge is preserved as much as possible (however, the edge also decreases definitely). It is expected that our approach, integrating the two methods, can achieve edge enhancement with almost no significant noise increase and can be applied to low- dose radiographs to improve image quality. To verify the proposed method’s effectiveness in reducing radiation dose in digital radiography, it was assessed quantitatively and qualitatively.
2. Methods
2.1. Proposed Method
The main steps of the proposed method include a previously reported wavelet coefficient adjustment technique for contrast enhancement [11] -[13] and a wavelet thresholding technique for noise reduction. Figure 1 shows a schematic diagram of the proposed method. As shown in Figure 1, the proposed method for denoising radio
Figure 1. Flow chart of the proposed method.
graphic images starts by decomposition of the original image by use of the discrete wavelet transform, which results in obtaining different detail wavelet coefficients (horizontal, vertical, diagonal). The three detail coefficients are then processed by use of a sigmoid-type transfer curve for adjustment of wavelet coefficient, followed by Bayes Shrink thresholding.
2.1.1. Sigmoid-Type Transfer Curve for Wavelet Coefficient Weighting Adjustment
A sigmoid-type transfer curve with a one-to-one mapping function is used for enhancement of image contrast. The mapping function was determined based on the following considerations: a) in the case of detail compo- nents at a specific level, high-value coefficients are weighted because they carry effective information; b) the coefficients at low levels are heavily weighted, because they carry detailed information, such as edge information; and c) the approximation coefficients are not manipulated in order to prevent image distortion.
In the wavelet decomposition of level j, the sigmoid-type transfer curves of wavelet coefficients can be expressed as follows:
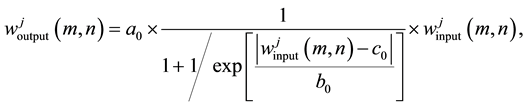 (1)
(1)
where
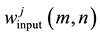 and
and
 represent input and output coefficients, respectively. a0, b0,
and c0 are constants. In practice, Equation (2) is used as the mapping function instead of
Equation (1). In Equation (2), the values of the coefficients are expressed in terms
of percentage for the ease of computation.
represent input and output coefficients, respectively. a0, b0,
and c0 are constants. In practice, Equation (2) is used as the mapping function instead of
Equation (1). In Equation (2), the values of the coefficients are expressed in terms
of percentage for the ease of computation.
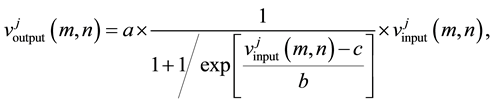 (2)
(2)
Here,
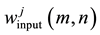 is the input
value expressed in terms of percentage. This value makes the mean of the absolute
values of the coefficients at level j equal to 50%.
is the input
value expressed in terms of percentage. This value makes the mean of the absolute
values of the coefficients at level j equal to 50%.
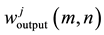 is the corresponding output value, also expressed in terms of percentage. The reason for utilization of percentage is that
by doing so the constants a, b, and c could be used independent of image characteristics.
The constants a, b, and c are determined depending on the extent of enhancement.
In this study, the value of a was computed by use of Equation (3):
is the corresponding output value, also expressed in terms of percentage. The reason for utilization of percentage is that
by doing so the constants a, b, and c could be used independent of image characteristics.
The constants a, b, and c are determined depending on the extent of enhancement.
In this study, the value of a was computed by use of Equation (3):
 (3)
(3)
where N represents the maximum decomposition level. Consequently, the lower the wavelet decomposition level j, the greater the gradient of the transfer curve becomes. The reason for making the value of a dependent on decomposition levels is that the wavelet coefficients at low-decomposition levels, which mainly contain information about edges, are highly weighted. The constant c was determined by use of Equation (4):
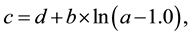 (4)
(4)
where d is a constant used for determining the inflection point of the sigmoid curve, and b represents a constant used for determining the gradient of the sigmoid curve. The values of b and d used in this study were 20 and 25, respectively [12] . The values were determined empirically.
2.1.2. Bayes Shrink Thresholding Technique
The wavelet transform, due to its excellent localization property, has become an indispensable image-denoising tool during the past two decades. Wavelet de noising attempts to remove the noise present in an image while preserving the image characteristics. Wavelet thresholding, first proposed by Donoho [4] , is a signal-estimation technique that exploits the capabilities of the wavelet transform for signal and image denoising. It removes noise by eliminating coefficients that are insignificant relative to some threshold. Therefore, the selection of the threshold is the most important step in wavelet-based denoising techniques.
Various threshold selection methods have been proposed, such as Visu Shrink [15] , Sure Shrink [16] , and Bayes Shrink [14] . In the Visu Shrink method, a universal threshold that is a function of the noise variance and the number of samples is developed based on the minimax error measure. The threshold value in the Sure Shrink method is optimal in terms of the Stein’s unbiased risk estimator. The Bayes Shrink method determines the threshold value in a Bayesian framework, through modeling of the distribution of the wavelet coefficients as Gaussian [17] . Several researchers have compared the three selection methods, and their results have shown that Bayes Shrink outperforms the other two methods [17] -[19] . In this study, we employed the Bayes Shrink method for denoising.
In the Bayes Shrink scheme, the threshold is determined for each sub and by assuming a generalized Gaussian distribution (GGD) [14] . The Bayes Shrink threshold, TB, is given as
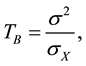 (5)
(5)
where σ2 is the noise variance and σX the signal standard
deviation. Suppose that the signal and the noise are independent of each other.
The estimated variance of the observed image,
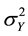 , can be written
as
, can be written
as
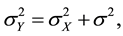 (6)
(6)
The estimated variance of signal
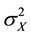 is then deduced by
is then deduced by
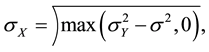 (7)
(7)
A robust estimator of the noise variance is obtained by
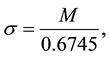 (8)
(8)
where M is the median value of the absolute wavelet coefficients in the first decomposition level. A detailed explanation of the Bayes Shrink method is given in [14] .
2.2. Data Acquisition
Images that were used for measurement of physical characteristics were acquired with use of a multipurpose phantom [20] . Figure 2 shows an example of phantom images. A computed radiography (CR) system (FCR

Figure 2. Examples of phantom images used for the measurement of physical characteristics. (a) Contrast detail curve; (b) MTF; (c) NPS; and (d) GLC using acrylic disk on Burger phantom.
XG-1, Fuji Photo Film, Tokyo, Japan) and an imaging plate (ST-VN, Fuji Photo Film, Tokyo, Japan) were used in this study. A pixel size of 0.1 mm and a quantization level of 10 bits were employed for data acquisition. The system parameter settings for the latitude (L) and sensitivity (S) were fixed at 3 and 200, respectively. Images were taken with a radiation quality of RQA-5 (HVL = 7.1 mm Al, 21 mm Al additional filtration) by using a tungsten target x-ray tube (Hitachi, Tokyo, Japan). The focal spot size of the x-ray tube was 0.6 mm. The source- to-image receptor distance was 190 cm. The amount of exposure was 4.63 × 10−7 C/kg (50 mAs). Twenty phantom images were obtained and used for measuring the presampled modulation transfer function (MTF), noise power spectrum (NPS), and gray level contrast (GLC).
Four different radiation levels were used for investigating the effect of the physical characteristics on the radiation dose. The 4 radiation level ratios with respect to the reference level, 4.63 × 10−7 C/kg, were 50/100, 64/ 100, 80/100, and 100/100.
A visual evaluation of wavelet-processed images of a human body phantom was performed to confirm the effectiveness of the proposed method in reducing radiation dose. An anterior-posterior (AP) projection of the hip joint and a lateral view of the lumbar spine on the human body phantom were exposed to various dose levels. These two images were also taken at four different radiation level ratios, 50/100, 64/100, 80/100, and 100/100, instead of the reference level that is commonly used in clinical radiology practice. In this study, the hip joint phantom was exposed at 70 kVp and 32 mAs, and the lumbar phantom at 82 kV and 64 mAs.
2.3. Measurement of Physical Characteristics
2.3.1. MTF
The presampled MTFs were measured with an angled-edge method [21] . The edge device was made of a 1-mm- thick sharp-edged tungsten plate whose dimensions were 10 × 10 cm2. The direction of the edge was oriented with a small angle (2˚ - 3˚). The edge spread function (ESF) in the direction perpendicular to the edge was then obtained. To reduce the noise in the edge profile, 20 representations of the sampled ESFs were generated from the region of interest (ROI). Then the ESFs were differentiated to obtain the line spread functions (LSFs), and the presampled MTFs were deduced by applying Fourier transformation to the LSFs [21] [22] . The resulting MTF was obtained by averaging the 20 MTFs.
2.3.2. NPS
NPS measurements were made by exposure of the imaging plate to a uniform beam of radiation. For determination of the NPS, a two-dimensional 2nd-order polynomial was fitted and subtracted to remove background trends. For the calculation, the central portion of each uniform image obtained was divided into 4 non-overlap- ping regions, 256 × 256 in size. A total of 80 regions were used. The NPS was calculated by applying the fast Fourier transform to each of the ROIs and then averaging the resulting spectrum estimates [23] [24] .
2.3.3. GLC
A commercially available Burger phantom (Kyoto Kagaku, Kyoto, Japan) was employed for measurement of GLC characteristics. In this study, the GLC was used to describe the relative contrast of an image, defined by

where Lacrylic, LBG, and LD represent the mean pixel value of an 8.0 mm diameter circle of an acrylic disk 8.0 mm in thickness, the mean pixel value of the background, and the gray level of the CR, respectively. The GLC ranged from 0 to 1.0. Image contrasts with different gray levels could be compared because the GLC was normalized by (LD ? 1). Low GLC corresponded to low contrast, while high GLC corresponded to high contrast. For clarifying the effect of the radiation dose on the GLC, dose ratios ranging between 100/100 and 50/100, instead of the standard dose, were measured.
2.4. Performance Comparison
In order to validate the superiority and effectiveness of the proposed method, the proposed method and 3 conventional methods, namely, the Wiener filter (WF) [25] [26] , Bayes Shrink method [14] , and sigmoid-type method [11] were compared. Table 1 shows various parameters of the three methods and the proposed method. The
Table 1. List of methods and their parameters.
WF used in this study was a pixelwise adaptive WF given as

where f(i, j) and g(i, j) are the pixel values of pixel (i, j) in the input image and the output image, respectively. μ and σ2 are the local mean and local variance, respectively, in the N-by-M local neighborhood of pixel (i, j) in the input image. M × N is the kernel size of the local region (a 5 × 5 matrix was used in this study as shown in Table 1). ν2 is the noise variance, which is the average of all the local variances in this study. Where the local image variance was large, the WF performed somewhat smoothly. Where the local image variance was small, the WF performed even more smoothly.
The proposed method and the above-described three methods were applied to the original images for performance comparison.
2.5. Visual Evaluations
A visual evaluation was conducted by five experienced radiological technologists. The images were displayed on a liquid-crystal display (1280 × 1024 matrix, LCD-1980SXi, Nippon Electric Company, Tokyo, Japan). The parameters of window level, window width, and display image size on the image display apparatus were fixed. Each observer reviewed the images independently. The reading time was not limited. The five radiological technologists independently evaluated the total depiction of each phantom image for diagnostic acceptability by using a 5-point grading scale (1, no depiction; 2, faint; 3, acceptable; 4, good; 5, excellent). Statistical analyses were performed with the Friedman test. When a statistically significant difference was found (p < 0.01) in the five images (the original and the four image-processed images) at each dose ratio, pairwise comparisons were performed with Scheffe’s method. Comparisons were made by use of five possible combinations, namely, WF-processed image, Bayes Shrink-processed image, sigmoid-processed image, proposed filter-processed image, and the original image.
3. Results
Figure 3(a) shows the MTF values for the original image and the four processed images. The MTF value for the sigmoid image was the highest, followed by that for the proposed image. Both MTFs were considerably superior to the original image over the entire spatial frequency range. In contrast, the MTF values obtained from the Bayes Shrink and the WF images were slightly lower than that of the original image. Figure 3(b) shows the NPS values. The NPS values for the sigmoid image were pronouncedly higher than those of the original image. The NPS values for the proposed image were slightly higher or similar to those of the original image. In contrast, the NPS values for the Bayes Shrink and WF images were lower than those for the original image.
Figure 4(a) shows the GLC as a function of the radiation dose ratio. There were no significant differences in any of the GLCs. Figure 4(b) and Figure 4(c), respectively, show the NPSs as a function of the dose ratio at spatial frequencies of 1 mm−1 and 4 mm−1 for the original image and the four processed images. Although the trend of the values measured from the proposed-method-processed image is similar to that measured from the original image in dose ratios ranging from 80/100 to 50/100, the NPSs for the proposed method showed improvement in noise level at the dose ratio of 50/100 at the spatial frequency of 4 mm−1.
Figure 5 illustrates the mean grades of visual evaluation for the hip joint and the lumbar spine at the four radiation dose ratios. In all cases, significant differences (p < 0.01) were found with the Friedman test at various radiation dose ratios. For the hip joint, the mean grade of the proposed method reached 3 points and was higher


Figure 3. (a) Presampled MTFs for the original image and the four processed images; (b) NPSs for the original image and the four processed images.



Figure 4. (a) Gray-level contrasts as a function of the dose ratio for the original image and the four processed images obtained using a Burger phantom. (b) The NPSs as a function of the radiation dose ratio, measured from the original image and the various images processed by the WF, BayesShrink, sigmoid-type, and the proposed methods at spatial frequency of 1 mm−1. (c) The NPSs at spatial frequency of 4 mm−1.
Figure 5. Mean grades of visual evaluation of the original and the four processed images for the hip joint and lumbar spine at the four radiation dose ratios, 100/100, 80/100, 64/100, and 50/100, in comparison to the standard dose. (a) hip joint (AP). (b) lumbar spine (lateral).
than those of the other methods tested at all radiation dose ratios. In the case of the lumbar spine, except for the radiation dose ratio of 50/100, the mean grade for the proposed method was higher than those of the other methods tested.
Figure 6 illustrates visual evaluation results for the hip joint (AP) and lumbar spine (lateral) at various radiation dose ratios by use of Scheffe’s method of paired comparisons. As shown in Figure 6, original image (Org) at 100/100 radiation dose ratio is located at the center (marked as zero) of the straight horizontal bar. The quality of the processed image was superior to that of the Org, if it had a higher score than the Org and there was a statistical significance. The quality of the processed image was inferior to that of the Org, if it had a lower score than the Org and there was a statistical significance. If the processed image had a similar score to that of the Org, the quality was considered to be equivalent to that of the Org. In terms of diagnostic acceptability, the proposed method provided significantly better results than those of the original image up to a 64/100 radiation dose ratio in the hip joint. When the radiation dose ratio was 50/100, no significant difference was found between the image processed by the proposed method and the original image.
In the case of lumbar radiographs, the results obtained from the proposed method were comparable to those of the original image up to a 64/100 radiation dose ratio. However, the proposed method tended to show unsatisfactory results for a 50/100 radiation dose ratio.
Figure 7 illustrates original and processed images of the hip joint and lumbar spine of the human body phantom, which were used for the visual evaluation.
4. Discussion
The proposed method provides the benefits of improved resolution and noise suppression. The experimental results demonstrated the method’s effectiveness in dose reduction without degradation in image quality at a lower dose as compared to the standard dose. In the MTF and NPS measurements (Figure 3), the physical properties of the images processed by use of the sigmoid function and Bayes Shrink methods show distinct differences. The sigmoid function yields improved spatial resolution characteristics with increasing noise. In contrast, the Bayes Shrink method provides improved noise properties, but deteriorating spatial resolution. The proposed method incorporates the sigmoid method into the Bayes Shrink algorithm. As a result, the proposed method shows better spatial resolution and noise properties compared to the original image.
In the GLC measurements (Figure 4(a)), there were almost no differences in any of the GLCs. This implies

Figure 6. Visual evaluation results using Scheffe’s method of paired comparisons of the original image (Org) at the radiation dose ratio of 100/100 and various images processed by the WF, BayesShrink (Bay), sigmoid (Sig), and the proposed (Pro) methods at radiation dose ratios of 100/100, 80/100, 64/100, and 50/100 in comparison to the standard dose. (a) Hip joint (AP). (b) Lumbar spine (lateral). There was a significant difference (p < 0.01) between the original image and the processed image at various dose ratios if the * mark is shown.
that contrast was independent of x-ray dose and the proposed method did not contribute to contrast enhancement in the GLC experiment. This result was expected because a thin acrylic phantom was used in the experiment and CR has the characteristic of a linear relationship between pixel value and x-ray dose. However, the contrast of signal edge in a low-dose image of a thick scatterer, such as the human body, will decrease, because low-dose radiation brings about an increase in blur and noise. In this study, the proposed method contributed to the contrast enhancement of signal edge. Our previous study [11] indicated the potential for the contrast enhancement of signal edge by measuring the contrast improvement ratio for chest radiographs, mammograms, and chest CT images. We will investigate this issue in detail in future research.
In Figure 4(b) and Figure 4(c), the NPS values of our proposed method were near to those of the original image at all radiation dose ratios except 100/100. The high NPS value of our method at the 100/100 radiation dose ratio might be due to the fact that some noise enhanced by the sigmoid-function method was not recognized as noise in the Bayes Shrink method, and thus did not decrease efficiently.
As shown in Figure 5 and Figure 6, the results of our study indicate that the proposed strategy significantly improves the quality of low-dose images such that CR images obtained at 50% and 64% of the standard dose level provide clear depiction in AP views of the hip joint and in lateral views of the lumbar spine, respectively, in terms of visual evaluation. In Figure 7, the visibility of the overall appearance of bones seems to be improved by the proposed method. This may be due to the improvement in resolution and the suppression of noise. Maintaining a well-balanced relationship among contrast, spatial resolution, and noise is important. From this point of view, the proposed method has a well-balanced filter for the AP view of the hip joint and the lateral view of the lumbar spine at a lower dose.
This study does have a limitation. The superiority of the proposed method was not demonstrated for the lateral lumbar spine when the radiation dose ratio was at 64/100 as compared to the standard dose. This issue may be overcome by optimizing parameters, such as b and d in Equation (4). To address this issue, further improvement of the proposed method is still needed.
Figure 7. Original phantom images and processed phantom images obtained using WF, Bayes Shrink, sigmoid, and the proposed methods. (a)-(e) Hip joint at the standard dose; (f)-(j) Lumbar spine at the standard dose.
5. Conclusion
In this paper, we proposed an improved wavelet-transform-based method for potentially reducing radiation dose while maintaining clinically acceptable image quality. The effectiveness of the proposed method was demonstrated quantitatively and qualitatively. The experimental results showed that the proposed method could improve resolution while keeping noise level within acceptable limits. Furthermore, the results validated the effectiveness of our proposed method in the reduction of radiation dose. Our visual evaluation showed that an approximately 40% - 50% reduction in the exposure dose might be achieved with the proposed method in AP views of hip joint radiographs and lateral views of lumbar spine radiographs. The proposed method has the potential to improve visibility in radiographs when a lower radiation dose is applied.
Acknowledgements
The authors also would like to thank the observers for their participation in visual evaluation.
References
- Gruber, M., Weber, M., Homolka, P., Nemec, S., Fruehwald-Pallamar, J. and Uffmann, M. (2011) Feasibility of Dose Reduction Using Needle-Structured Image Plates versus Powder-Structured Plates for Computed Radiography of the Knee. American Journal of Roentgenology, 197, 318-323. http://dx.doi.org/10.2214/AJR.10.5505
- Liu, X., Shaw, C.C., Lai, C.J. and Wang, T. (2011) Comparison of Scatter Rejection and Low-Contrast Performance of Scan Equalization Digital Radiography (SEDR), Slot-Scan Digital Radiography, and Full-Field Digital Radiography Systems for Chest Phantom Imaging. Medical Physics, 38, 23-33. http://dx.doi.org/10.1118/1.3519903
- Schaefer-Prokop, C., Neitzel, U., Venema, H.W., Uffmann, M. and Prokop, M. (2008) Digital Chest Radiography: An Update on Modern Technology, Dose Containment and Control of Image Quality. European Journal of Radiology, 18, 1818-1830. http://dx.doi.org/10.1007/s00330-008-0948-3
- Donoho, D.L. (1995) De-Noising by Soft-Thresholding. IEEE Transactions on Information Theory, 41, 613-627. http://dx.doi.org/10.1109/18.382009
- Jansen, M., Uytterhoeven, G. and Bultheel, A. (1999) Image De-Noising by Integer Wavelet Transforms and Generalized Cross Validation. Medical Physics, 26, 622-630. http://dx.doi.org/10.1118/1.598562
- Harpan, M.D. (1999) A Computer Simulation of Wavelet Noise Reduction in Computed Tomography. Medical Physics, 26, 1600-1606. http://dx.doi.org/10.1118/1.598654
- Okamoto, T., Furui, S., Ichiji, H., Yoshino, S., Lu, J. and Yanagi, T. (2004) Noise Reduction in Digital Radiography Using Wavelet Packet Based on Noise Characteristics. Journal of Signal Processing, 8, 485-494. http://dx.doi.org/10.2299/jsp.8.485
- Tischenko, O., Hoeschen, C. and Buhr, E. (2005) Reduction of Anatomical Noise in Medical X-Ray Images. Radiation Protection Dosimetry, 114, 69-74. http://dx.doi.org/10.1093/rpd/nch518
- Ferrari, R.J. and Winsor, R. (2005) Digital Radiographic Image Denoising via Wavelet-Based Hidden Markov Model Estimation. Journal of Digital Imaging, 18, 154-167. http://dx.doi.org/10.1007/s10278-004-1908-3
- Yasuda, N., Ishikawa, Y. and Kodera, Y. (2005) Improvement of Image Quality in Chest MDCT Using Nonlinear Wavelet Shrinkage with Trimmed-Thresholding. Japanese Journal of Radiological Technology, 61, 1599-1608.
- Lee, Y., Tsai, D.Y. and Suzuki, T. (2008) Contrast Enhancement of Medical Images Using Sigmoid-Type Transfer Curves for Wavelet Coefficient Weighting Adjustment. Medical Imaging and Information Sciences, 25, 48-53.
- Tsai, D.Y. and Lee, Y. (2003) A Method of Medical Image Enhancement Using Wavelet Coefficient Mapping Functions. Proceedings of IEEE International Conference on Neural Networks and Signal Processing, 2, 1091-1094.
- Watanabe, H., Tsai, D.Y., Lee, Y., Matsuyama, E. and Kojima, K. (2011) An Integrated Method of Wavelet Coefficient Thresholding for Reducing Radiation Dose While Maintaining Diagnostic Image Quality. Medical Imaging and Information Sciences, 28, 51-56.
- Chang, S.G., Yu, B. and Vetterli, M. (2000) Adaptive Wavelet Thresholding for Image Denoising and Compression. IEEE Transactions on Image Processing, 9, 1532-1546. http://dx.doi.org/10.1109/83.862633
- Donoho, D.L. and Johnstone, J.M. (1994) Ideal Spatial Adaptation via Wavelet Shrinkage. Biometrika, 81, 425-455. http://dx.doi.org/10.1093/biomet/81.3.425
- Donoho, D.L. and Johnstone, I.M. (1995) Adapting to Unknown Smoothness via Wavelet Shrinkage. Journal of the American Statistical Association, 90, 1200-1224. http://dx.doi.org/10.1080/01621459.1995.10476626
- Zhang, M. and Gunturk, B.K. (2008) Multiresolution Bilateral Filtering for Image Denoising. IEEE Transactions on Image Processing, 17, 2324-2333. http://dx.doi.org/10.1109/TIP.2008.2006658
- Sendur, L. and Selesnick, I.W. (2002) Bivariate Shrinkage Functions for Wavelet-Based Denoising Exploiting Interscale Dependency. IEEE Transactions on Signal Processing, 50, 2744-2756. http://dx.doi.org/10.1109/TSP.2002.804091
- Karthikeyan, K. and Chandrasekar, C. (2011) Speckle Noise Reduction of Medical Ultrasound Images Using Bayesshrink Wavelet Threshold. International Journal of Computer Applications, 22, 8-14. http://dx.doi.org/10.5120/2614-3646
- Watanabe, H., Tsai, D.Y., Lee, Y., Nakamura, T., Miyazaki, M., Kuramochi, Y. and Kojima, K. (2009) Evaluation of Irreversible Compressed Images in Computed Radiography Using Physical Image Quality Measures. Japanese Journal of Radiological Technology, 65, 1618-1627. http://dx.doi.org/10.6009/jjrt.65.1618
- Samei, E., Flynn, M.J. and Reimann, D.A. (1998) A Method for Measuring the Presampled MTF of Digital Radiographic Systems Using an Edge Test Device. Medical Physics, 25, 102-113. http://dx.doi.org/10.1118/1.598165
- Flynn, M. and Samei, E. (1999) Experimental Comparison of Noise and Resolution for 2k and 4k Storage Phosphor Radiography Systems. Medical Physics, 26, 1612-1623. http://dx.doi.org/10.1118/1.598656
- Neitzel, U., Gunther-Kohfahl, S., Borasi, G. and Samei, E. (2004) Determination of Detective Quantum Efficiency of a Digital X-Ray Detector: Comparison of Three Evaluations Using a Common Image Data Set. Medical Physics, 31, 2205-2211. http://dx.doi.org/10.1118/1.1766421
- Samei, E. and Flynn, M.J. (2002) An Experimental Comparison of Detector Performance for Computed Radiography Systems. Medical Physics, 29, 447-459. http://dx.doi.org/10.1118/1.1449873
- Bankman, I.N. (2000) Handbook of Medical Imaging. Academic Press, San Diego, 24-26.
- Lim, J.S. (1989) Two-Dimensional Signal and Image Processing. Prentice Hall, Englewood Cliffs, 548.






