Engineering
Vol.09 No.02(2017), Article ID:74489,51 pages
10.4236/eng.2017.92010
The Study of Condensation Processes in the Low-Temperature Short Heat Pipes with a Nozzle-Shaped Vapour Channel
Arkady V. Seryakov
LLC Research and Development Company “Rudetransservice”, Veliky Novgorod, Russia

Copyright © 2017 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: December 24, 2016; Accepted: February 25, 2017; Published: February 28, 2017
ABSTRACT
The results of researches of condensation processes in the vapour channel similar to the Laval nozzle of short linear heat pipes are presented. Capacitive sensors are additionally installed in cooled top covers of the heat pipes, and electromagnetic pulses were supplied to them from the external generator. At heating the heat pipe evaporator, starting from a certain thermal power threshold value, electromagnetic pulses became modulated. It is related with the formations of the boiling process in the capillary-porous evaporator and large amount of vapour over it. Boiling process results in rapid increase of the pressure under which the average temperature of the evaporator occurs to be less than the boiling temperature of the working fluid under increased pressure. Considering condensation of excess vapour, this leads to repeated initiation and extinction of the boiling process in the evaporator, which reflects in pressure pulsations in the vapour channel. Pressure pulsations cause modulating effect on electromagnetic impulses. Pulsations frequencies are measured as well as their dependence from overheating of the evaporator. Using the capacitive sensors and a special electronic equipment we measured the local thickness of the working fluid at the condensing surface inside the heat pipes. Time-averaged values of the condensate film thickness are measured, depending on the heat load on the capillary-porous evaporator. The measurement error does not exceed 2 × 10−3 mm. It is demonstrated that the condensate film thickness lessens sharply with the increase of the heat load on the evaporator of a Laval-like low-temperature heat pipe, while the heat resistance of the film on the condensing surface reaches 60% of the total heat resistance of heat pipe with the capillary-porous evaporator.
Keywords:
Heat Pipe, Compact Open Capacitance Sensor, Thickness of Condensate Film, Rotational Flow

1. Introduction
Intense advancement and practical use of short low-temperature range heat pipes (HPs) initiate a thorough study of characteristics of the inner flow of the working fluid’s condensate film inside HPs on the condensing surface. Fluid condensate films in low-temperature HPs have small thickness (0.001 to 0.1 mm) and low heat resistance that determine the high performance of HPs. Formation of complex three-dimensional flows of moist vapour near the HPs condensing surface, mass transfer into the film and presence of a relative motion of phases during condensation cause a generation of fluctuations, an occurrence of additional shearing and normal stresses at the film and vapour border, and an instability of the film thickness.
In addition to the above, with a high heat load on the capillary-porous evaporator, the flow in the vapour channel of short open-circuit HPs becomes pulsating [1] [2] [3] [4] , which is associated with a start of the boiling process in the evaporator and formation of a large amount of vapour above it. Occurrence of velocity and pressure pulsations in the vapour channel of short HPs leads to the modulation of fluid film thickness on the condensing surface with a pulsation frequency, what allows using the capacitance method to measure the pulsations frequency and average local thickness of the working fluid condensate film. Detailed measurements of the fluctuation frequency in short HPs vapour channel are shown in [1] [2] .
Experimental determination of thickness, temperature and, subsequently, flow velocity of the fluid film on the condensing surface inside HPs represents an important practical problem which, until recently, has been restrained by the absence of requisite gauging equipment that needs to be inserted inside the metal body while making no perturbation impact on HPs.
To highlight the importance of determining the film thickness, it should be also mentioned that once the local liquid film thickness is known, it becomes easier to estimate the thermal power, thermal resistance of the HPs, the frequency of rotation of the liquid film, hence the liquid and vapour relative velocities as well as the amplitude of pulsations and the coefficient of surface friction of vapour and condensate film.
Ultrasound may promote the emergence of local areas of cavitation and intense light or x-ray beams may promote the evaporation of the liquid film on the transparent condensing surface inside HPs.
Capacitance-based methods provide a particularly attractive option since the method of detection is non-intrusive, highly sensitive and suitable for electrically conducting or insulating liquids.
Open capacitance sensor method is based on the fact that when two metal plates under the layer of liquid submitted to an electric current are faced parallel each other in one plane, a capacitance is created which value will depend on the plate area, the distance of the plates, the thickness and dielectric constant of the liquid over them.
This paper discloses the results of the capacitance method usage for a study of condensation processes inside short metal-cased low-temperature HPs, and a measurement of instantaneous values and time-averaged thickness of the working fluid condensate film on the condensing surface, depending on the heat load on the evaporator.
To measure the film thickness, we used the standard method of registering the condenser’s electric capacity variations in line with the thickness alterations of the working fluid condensate film on the located flush with the condensation surface gauging surface of sensor electrodes. A number of studies concerning application of the capacitance method for determination of the thickness of the working fluid layer in pipes are given in the [5] - [12] .
Some of the first, who used a capacitive technique to control fluid flow along the vertical surface were Ducler and Bergelin [5] . They developed a capacitance device and were able to measure water film thicknesses down to 0.5 mm with an error inferior to 10%. In their paper, they highlighted the fact that capacitive method is simple to implement, non-intrusive and presenting a reasonable accuracy.
Rogovaya et al. [6] employed more complex capacitance probe with two different counter electrodes. One of the electrodes is fixed flush to the wall surface, the other is rigidly connected to a micrometer, allowing it to move perpendicular to the wall. The measurements were made in the following way: they act on the screw micrometric order to bring the movable electrode in contact with the top of the waves a series of 10 steps of 0.1 mm each. The values of the capacities measured in the course of a changes show dispersion less than 5%.
More recently Ozgu et al. [7] have developed a variant of the capacitance method also with two electrodes placed on one side of the liquid film, side by side on the insulating wall of the channel. In this case the film is analyzed in a direction parallel to the wall but non-perpendicular as in the method proposed by Rogovaya. Thus electrodes used have a spacing adjustable, allowing for a film thickness given to work in the optimal conditions of determination of the value of the capacity.
Thorncroft and Klausner [8] used a parallel-plate capacitance sensor to measure liquid film thickness for horizontal, vertical upward and downward two-phase flows in a planeparallel channel. The capacitance was measured with a commercial instrument presenting a resolution of 0.1 fF and accurate to 0.1% of full scale. A simplified model was developed for predicting capacitance output as a function of the film thickness.
Krotov and Alekseenko et al. [9] [10] [11] adopted the same capacitance method for determine the instantaneous and average thickness of a liquid film. Their goal was to calculate the critical Reynolds number corresponding to the occurrence waves at the surface of the film, a number that is a function of its average thickness, the velocity, the number and energy of the waves.
Recently Chen et al. developed coplanar capacitive sensor for microfluidic devices [12] . Coplanar electrodes can give a more compact design and it allows to create arrays of measuring electrodes with the increased value of the capacitive signal. However, these enviable advantages lead to the averaging effect and cannot be applied to measure the local thickness of the liquid film on the condensation surface inside metal HPs.
The range of film thicknesses that can be measured depends primarily on the dielectric permeability of the fluid. The most accurate and reliable results can be obtained when the dielectric permeability of the fluid and vapour (gas) phases differs by five or more time,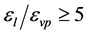 . In such case, even with compact electrodes, the capacitance sensor has sufficient sensitivity of 10 - 30 pF/m (0.01 - 0.03 pF/mm), which is normally sufficient when using gauges with a measuring sensitivity for electric capacity of 10−4 pF and higher. With a minor difference between the dielectric permeability of the fluid and vapour phases
. In such case, even with compact electrodes, the capacitance sensor has sufficient sensitivity of 10 - 30 pF/m (0.01 - 0.03 pF/mm), which is normally sufficient when using gauges with a measuring sensitivity for electric capacity of 10−4 pF and higher. With a minor difference between the dielectric permeability of the fluid and vapour phases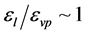 , the measuring sensitivity and broad bandness using a compact capacitance sensor are increased due to the frequency growth and application of the differential method, related to the measurement of frequency differences of measuring and reference high-frequency generators and in the measurement control using a PC.
, the measuring sensitivity and broad bandness using a compact capacitance sensor are increased due to the frequency growth and application of the differential method, related to the measurement of frequency differences of measuring and reference high-frequency generators and in the measurement control using a PC.
2. Capacitance Sensor: Design and Application
The main idea of this work is the design and development of capacitance open sensors which can be directly integrated with the condensation surface inside metal HPs. This paper presents the presently fullest classification of various designs of the capacitance sensors used when studying hydrodynamics of the fluid film flows in the channels [11] . Our compact open capacitance sensor is an advanced and upgraded version of one of the sensors that is presented therein and has received a patent [13] . The developed sensor enables us to perform measurements of local characteristics of the film flows―primarily, the film thickness and temperature, without making any major disturbances in the flow.
To measure the fluid condensate film thickness, short HPs were used whose vapour channel was made in the form of a nozzle, similar to the Laval nozzle [14] [15] . The HPs are described in details below.
The capillary-porous evaporator 7 is constructed of 43 circular layers of thin stainless steel net. Each layer is 0.07 mm thick with the mesh size of 0.04 mm and the aggregate thickness of 3 mm; all layers are spot-welded to the flat bottom lid 5. Outer diameters of the circular layers gradually decrease in such a manner that the lateral side of the assembled evaporator forms a pointed cone with a 45˚ total point angle that aligns with the angle of the end part of the capillary-porous insert 4.
The evaporator as a whole is further equipped with 4 vapour injection channels 6 with increasing diameter of 1 mm, 1.1 mm, 1.2 mm and 1.3 mm diameter that are inclined to the longitudinal axis of HP at a specific angle and create a swirling jet stream of vapour.
The capillary-porous insert 4 is assembled on a dedicated profiled frame made of layers of thin stainless steel net same as the evaporator. Each layer is 0.07 mm thick with mesh size of 0.04 mm, the total thickness of the insert is 1.5 mm at the edges and 7.5 mm at the critical diameter of the inner nozzle. All layers of the insert are radially stitched together along the forming insert with a thin wire 0.05 mm in diameter and stitch spacing of 5 - 7 mm. Eight lines of the wire stitches that radially fix the net layers together are tilted by 45˚ towards each other and form a rigid structure of the capillary-porous insert with an inner vapour channel made in the form of a nozzle, similar to the Laval nozzle. At the edge of insert 4 that is adjacent to the evaporator 7, an end portion is placed; its total angle is somewhat wider than that of the diffuser portion of the vapour channel and equals 45˚. The longitudinal length of the end portion is 3 mm and matches the thickness of the evaporator 7 exactly. The 45˚ angle of the end portion of insert 4 is formed by the gradually decreasing net layers’ lengths, from the outer layer to the inner one, and matches the angle of the evaporator 7 exactly. The multilayered evaporator with a tapering lateral side is tightly inserted into the rigid capillary-porous insert 4 at the full length of the end portion and is spot-welded to it in 8 spots along the perimeter of the insert. After being cooled down at the boiling temperature of fluid nitrogen 77 K (−196˚С), the assembled capillary- porous insert, together with the evaporator on the flat bottom lid 5, is tightly inserted in the stainless steel cylindrical shell 2 of the HP.
Porosity of the insert and evaporator is 72% and together they form one hydraulic system designed to deliver the service fluid to the evaporator when the HP is operating.
The HP length is 100 mm, its diameter is 20 mm, the max. diameter of the vapour nozzle in the convergent and divergent regions is 16 mm, the critical nozzle diameter is 4 mm, the length of the nozzle convergent region is 13 mm, the total angle of the convergent region is 41˚, the length of the nozzle divergent region is 81 mm, the total angle of the divergent region is 8.5˚, and the length of the cylindrical region in the nozzle throat section is 1 mm.
The compact open capacitance sensor constitutes the following device whose appearance is shown in Figure 1. The sensor’s body is made in the form of a flat circular flange 5.5 mm in diameter and 1 mm thick, with two cylindrical through bores 1 mm in diameter each that are arranged symmetrically with respect to the longitudinal axis of the flange, 2 mm from each other. Each through bore has vacuum-tight glass-to-metal seals 1 mm in diameter, in compliance with the
Figure 1. Compact open capacitance sensor layout. 1: flange with a gauging surface; 2: glass insulators; 3: gauging electrodes with gauging end surfaces; 4: ground electrode. The top surface is polished and called a gauging surface of the sensor.
national standard GOST 107.460092.002-86. Two gauging electrodes are tightly fixed in the vacuum-tight glass-to-metal seals, each of them 0.5 mm in diameter and 10 mm in length. The space between the gauging electrodes’ axes is a = 2 mm. A ground electrode 0.5 mm in diameter and 10 mm in length is additionally welded to the external surface of the flange.
The flange and gauging and ground electrodes of the open capacitance sensor are made of 29 NK kovar with thermal coefficient of linear expansion of ~5 × 10−6 К−1, density of 8350 kg/m3 and thermal conductivity of 19 W/m・K.
Leak-tight glass-to-metal seals are made of glass C48-2 with thermal coefficient of linear expansion of ~4.9 × 10−6 К−1, density of 2550 kg/m3, thermal conductivity of 8.5 W/m・K and softening temperature of ~843 K (570˚С). The dielectric permeability of glass C48-2 is εgl = 5.2, the loss-angle tangent at the electromagnetic waves frequency of 106 Hz does not exceed 28 × 10−4 and the specific electrical resistivity of glass is 1014 Ohm・m.
Flat gauging surface of the sensor is polished, its undulation not exceeding 0.63 μm including the surface of gauging electrodes and glass-to-metal seals.
The resistance of electrical insulation in the gauging electrodes is more than 2 × 1011 Ohm, the electrical resistance of the electrodes is not more than 0.7 Ohm, the operating voltage is under 500 V, the break-down voltage is ~1500 V, and the operating temperature range of compact open capacitance sensors is 77 K ÷ 473 K.
The vacuum-tight glass-to-metal seals of capacitance condensation sensors are characterized by high mechanical stability that provides means to sustain the excessive pressure up to 30 bar, and by high air-tightness or low gas permeability (gas leakage) that does not exceed 10−9 mbar・l・s−1 (10−5 Pa・m3・s−1). The air-tightness of glass-to-metal seals of the compact capacitance sensor was determined through the standard method for measuring the gaseous helium leakage rate using a model vacuum chamber and a leakage detector GTI-6.
The lack of aging materials (plastic masses, adhesives, organic materials, etc.) in the structure of our open capacitance sensors results in the high stability of their features supported by the value permanence of insulation resistance and self-capacitance of the first sensor specimens produced since 1990. In Figure 2 shows a detailed diagram of embedding of the capacitive sensors in the HPs top cover.
The micro-thermistor is 0.2 mm in diameter and is electrically insulated from the HP lid. The HP condensing surface of the top lid 1 and radially oriented end faces of the gauging electrodes of the capacitance sensor are also shown here.
3. Capacitance Sensor: Calibration
The sensor calibration is performed after the sensor is manufactured and the gauging surface is coated with a thin protective dielectric layer, e.g. Epilam Avtokon-0.5, whose thickness is 3 × 10−9 m (30 Ǻ). Ultra-pure diethyl ether С4H10O, ultra-pure ethanol С2H5OH and specially prepared distilled water were selected as working fluids for the calibration process. Purity grade of the final
Figure 2. Layout of the installation of two capacitance sensors into the top lid of the HP: 1: top lid with a smooth surface made of stainless steel 1Х18Н9Т; 2: actual capacitance sensors that are laser welded to the lid 1 along their perimeter, herewith the polished gauging surface of sensors is flush-lined with the lid’s inner surface; 3: glass insulators (glass-to-metal seals); 4: gauging electrodes of both sensors; 5: fastening nut of the HP filling unit that is welded to the inner surface of the lid 1; 6: screw plug of the HP filling unit; 7: capacitance sensor’s ground electrode; 8: micro-thermistor that is a sensing element of thermistor CT3-19 and is laser welded to the tangential oriented end faces of the electrodes of one of the capacitance sensors.
water was verified according to the value of specific electrical resistance whose value was not less than (18 − 20) × 106 Ohm・sm. The information on the static dielectric permeability of calibration fluids was obtained from [16] - [29] . The static dielectric permeability of diethyl ether in the temperature range (170 - 300) К can be presented by the equation, received us by the mathematical treatment of the published results [16] - [23] :
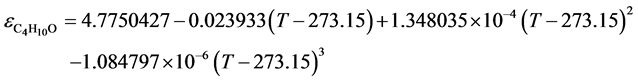 (1)
(1)
The standard deviation is σ = 0.037349, R2 = 0.999575.
The static dielectric permeability of ethyl alcohol can be presented by the equation, received us by the mathematical treatment of the published results [16] [17] [24] [25] [26] [27] in the temperature range (285 - 345) К:
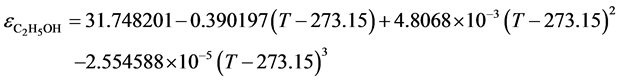 (2)
(2)
The standard deviation is σ = 0.502725, R2 = 0.954628.
The presently fullest informational base [28] [29] was used for the water and, within the temperature range 273 - 373 К, the static dielectric permeability of water can be presented by the equation stated there:
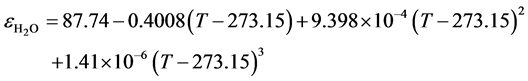 (3)
(3)
The calibration process consists in experimental determination of the sensor capacity at the independent measurement of the calibration fluid layer thickness over sensors measuring surface under constant and uniform temperature of the fluid and sensor.
Moreover, to increase the measurement accuracy of fluid film thickness on the condensation surface inside of HP, when calibrating the capacitance sensor it is required to remodel identically the induced electric fields around the measuring electrodes of the sensor, flush-mounted to the internal surface of the top cover of HP (see Figure 3).
To solve this problem the calibration was performed directly in the fragment of the standard HP with identical body and top cover with a smooth surface and with two mounted capacitance sensors, one of which was equipped with microthermistor. Herewith, the HP fragment presents vertically oriented upturned body cavity with the top cover and sensors mounted in it. The HP fragment layout with the upturned top cover is shown in Figure 4, way of flush mounting of capacitance sensors with internal surface of the top cover is detailed in Figure 2.
The HPs fragment as reversed body cavity with mounted cover and capacitance sensor is hermetically fixed in specially designed experimental test installation, which layout is shown in Figure 4.
Figure 3. layout of HP equipped with capacitance sensors: 1: flat upper lid with a smooth surface; 2: cylinder body of HP; 3: cone-shaped turbulence agitator; 4: capillary-porous insert defining the vapour channel’s form; 5: flat bottom lid; 6: injector channels; 7: capillary-porous evaporator; 8, 9: capacitance sensors, one of which is intended for a condensate film thickness measurement, while another one has a sensing element of CT3-19 thermistor mounted on its electrodes to measure the film temperature.
Figure 4. Layout of the experimental test installation with the mounted HPs fragment for capacitance sensor calibration.
The capacitance sensor 1 designed for calibration, is mounted in the cover of the upturned HPs fragment, as shown in Figure 4, herewith, elements surrounding the sensor precisely match with metal distribution when measuring the condensate layer thickness in the working standard HPs. In the upturned cover 2 opposite to the calibrated capacitance sensor, near the second sensor with microthermistor, there is the through opening 0.25 mm in diameter with the hermetically inserted measuring junction (short) of the differential thermocouple copper-constantan. The surface of the measuring junction matches the condensation surface of the top cover 2, and allows controlling temperature of the calibration fluid film at small thickness. The second junction of the differential thermocouple is constantly contained in the Dewar vessel filled with dispersed mixture of fine cracked ice and water at zero temperature (273.15 K). The HP fragment with shortened body (shell) 3 is hermetically inserted in the bottom opening of the base plate 4. External surface of short HP segment is surrounded with thermo stabilizing sheath 5 with flowing water, which temperature and flow rate are maintained by the external thermostat. The water temperature is Т = (298 ± 0.03) К.
In the upper portion of the base plate 4 there is the additional top opening extended to the HP body edge in the depth and displaced some distance away from the longitudinal axis of the HP. The flexible bellows 6 made of brass L80 and is mounted in this top opening in the plate 4. The sealing gland 7 is also hermetically fixed in the upper portion of the bellows 6. The movable measuring glass capillary 8 with outer diameter 1 mm and inner diameter 0.4 mm, is disposed inside of the central channel of the sealing gland 7. Hermetic sealing of the bellows 6 joint is performed using pure tin with THP000. Displacement value of the top opening, with respect to the longitudinal axis of the HP, is set in such a way that the capillary 8 never contacts the internal wall surface of the HP body, when moving up and down.
Brass sealing gland 7 is made as standard teflon seal with central through channel 1.05 mm in diameter, in which the glass capillary 8 is inserted, and with top nut adjusting compression efficiency of the teflon seal. This structure make it possible for the capillary 8 to realize longitudinal movement without affecting the hermeticity of the internal space of the bellows 6 and the HP fragment 3. Moreover, the bellows 6 itself can be compressed and stretched in longitudinal direction, herewith, thanks to the guard ring 9 with teflon coated internal surface, vertical orientation of bellows 6 and the entire sealing gland 7 is preserved. The guard ring 9 can obtain permanent position in space due to the lateral rod 10, securely fixed in the fitting 11, which is supported by the base plate 4 through the vertical rod 12.
On the support platform of the sealing gland 7 the hard HRC 45 disk 13, securely fixed by internal thread having ground top surface, and the extendable measuring rod 14 of the micrometer depth gauge 15 of GM type, is thrust against that top surface. The micrometer depth gauge 15 is securely fixed in the fitting 16 using the vertical rod 17, supported by the base plate 4. The limit of the absolute measurement error and length setting (adjusting) using the micrometer depth gauge is ±2 μm, sensitivity (scale increment) of the micrometer depth gauge is 0.01 mm.
Upper portion of the measuring glass capillary 8 is continued with thin flexible tube 18, which through the valve 19 is connected to the membrane electrical contact pressure sensor 20, which inlet A and outlet B are shunt using bypass valve 21. Sensor membrane is fabricated from steel foil 1Х18Н10Т 0.04 mm in thickness, membrane diameter is 100 mm, and sensor excessive pressure sensitivity is 0.5 Pa.
In the gaseous cavity of the HP short gaseous capillary 22 is inserted, which upper portion is connected to the outlet B of the membrane pressure sensor 20 and is vented to atmosphere through the valve 23.
The filling capillary 24, touching upon the bottom (cover) of the HP, through the inlet line the upper portion of this capillary is connected to the valve 25 and there through to the filling container 26, which can be made as a regular injection syringe with narrow needle.
The measuring glass capillary 8 is disposed at the opposite from the calibrated capacity sensor portion of the HP fragment near the microthermistor and thermocouple, the filling capillary 24 is disposed close to the measuring capillary, and is shown differently in the Figure 4 only because of the two-dimensional imaging.
There are valves 27 and 28 arranged on the top cover of the filling container 26. The container 26 can be filled with the calibration fluid (water, diethyl ether, and ethanol) through the valve 27, whereas through the valve 28 the excessive gas (argon) pressure can be supplied from the vessel 29 via the valve 30. Furthermore, the excessive gas pressure can be supplied to the measuring capillary 8 from the vessel 28 through the valve 31. Diameter of capillaries 8, 22 and 24 is 1 mm, the inner diameter is 0.4 mm.
The calibration process of the capacity sensor is performed in the following manner. The HP fragment is filled with large portion of the calibration fluid for a goodly proportion of the internal volume, and the fluid is immediately removed through the capillary 24. This procedure results in guaranteed formation of the molecular thickness film of the calibration fluid over the entire internal surface of the HP fragment, including the capacity sensor, what remarkably simplifies the wetting process of these surfaces at next filling of the fragment with small controlled quantity of fluid. The measuring capillary 8 is elevated and blown with gas portion from the vessel 29 through the opened valves 30, 31 and 23, fluid portion is removed from the internal cavity of the capillary.
The filling container 26 is filled with prepared calibration fluid (water, ethanol or diethyl ether). The top nut of the sealing gland 7 is released and the measuring capillary 8 is partially extended outside at ~10 mm. The bellows 6 is compressed approximately at 10 mm length, and the extendable measuring rod 14 of the micrometer 15 is unscrewed down until close contact of the rod 14 and the hard disk 13, what make it possible to hold the bellows 6 in compressed position. The measuring glass capillary 8 is pushed into the HP body cavity through the sealing gland channel, in such a way that the capillary end contacts the HP cover 2 surface. The top nut of the sealing gland 7 is slightly tighten, thereby fixing the measuring glass capillary 8 in contact with the internal surface of the HP top cover 2. Hence, the “zero level” of the measuring capillary 8 with respect to the internal surface of the HP cover 2 and concurrent to it with the measuring surface of the capacitance sensor can be successfully provided. The sensor capacity is measured in “dry” state, only the presence of the molecular thickness fluid film on the measuring surface of the sensor is confirmed.
The measuring rod 14 of the micrometer depth gauge 15 is rotated, and the sealing gland 7 together with the capillary 8 is shifted upwards at required distance, for instance 0.1 mm. By means of elastic stiffness of the compressed bellows 6, the raising goes smoothly, herewith vertical upward movement of the sealing gland 7 and measuring capillary 8 is assured with the guard ring 9. The movement comes upward vertically at specified upward value 0.1 mm.
The valve 25 is opened and the HP body cavity starts to fill slowly by injection of small drops of the calibration fluid, which properly spread over the condensation surface and measuring surface of the capacitance sensor, wetting them. As the wetting fluid touches the lower end portion of the measuring capillary 8, capillary elevation of the fluid goes approximately by 5 mm. The pressure surge in the measuring capillary reaches ΔP ~ 50 Pa, what allows fixing it reliable, using the membrane pressure sensor 20, where after the valve 25 closes. The calibration fluid covers the internal surface of the HP cover and measuring surface of the capacitance sensor with 0.1 mm layer. Systematic inaccuracy of setting (adjusting) and measuring the calibration fluid level over the capacitance sensor surface inside the HP segment by means of drawing a portion of the wetting fluid into the measuring capillary at capillary elevation and non instantaneous valve closing, does not exceed 0.001 mm.
Significant circumstance improving accuracy of measuring of fluid film thickness when calibrating the capacitance sensor, is systematic motion of the measuring rod 14 of the micrometer depth gauge 15 in one direction (upward) at all measurements, what reduces influence of the feed screw float of the micrometer 15.
Sensor’s capacity was measured using alternating current bridge Р5083 with absolute measurement error less than 10−5 pF. Temperature of the thermistor CT3-19 and thermal electromotive force of the thermocouple were measured using voltmeter AKIP B7-78 with measurement error 0.1 μV.
Because of comparatively small sensor capacity, influence of the supply wires capacity becomes significant. For thermal insulation was used twisted pair of shielded supply lines 0.5 mm in length. The wire shield was grounded and this was not resulted in marked frequency shift.
Further, the measuring rod 14 of the micrometer depth gauge 15 is moved upward by specified value, herewith the end portion of the measuring glass capillary 8 is lifted upward by this value. The valve 21 is opened and the membrane pressure sensor is return back to initial open state. Fluid plug is blown out from the measuring capillary 8 by supplying small portion of gas from the vessel 29 through the open valves 30, 31 and 23, in addition the valve 19 is closed. The pressure inside the HP body equals the atmospheric pressure. The valve 23 is closed. The next supply of small calibration fluid drops in the HP body is initiated until its level reaches the bottom end of the measuring capillary 8, what causes capillary elevation of the fluid approximately by several millimeters.
The calibration of the capacitance sensor was performed with release of small portions of gas into the atmosphere through the valve 23 every time the measuring capillary 8 was blown, herewith the pressure increase inside the HP internal body cavity was not higher than 0.01 bar. Special purity argon which is slightly soluble in fluids was used as the blowing gas, and its influence on fluid permittivity.
The sensor capacity variation can be neglected. Results for capacitance sensor calibration using micrometer depth gauge 15 GM type, are shown in Figure 5.
Figure 5. Calibration results for the capacitance sensor. 1: “drowned” capacitance sensor, when the calibration fluid (water) layer lies directly above the gauging surface of the sensor; 2: “dry” capacitance sensor in an inverted position above the surface of the calibration fluid (water) surface that approaches the gauging surface of the sensor. Direct scale from 0 to 8・mm is intended for the “drowned” sensor, curve 1; inverse scale from 8 to 0 mm is intended for the “dry” sensor, curve 2. Starting with the fluid layer thickness of h = 2 mm, which is equal to the distance between electrodes a, the sensor capacity growth sharply reduces, but once the layer thickness reaches h = 3.5 mm, the growth virtually recedes down to zero. It means that the capacitance sensor is insensitive within this thickness range of the fluid layer and defines a transition to the saturation state. The transition to the saturation state is caused by the closure of the electric field within the penetration (distribution) depth of the field Λ ~3.5 mm and by a virtual absence of the field beyond this depth Λ. All the details of the calibration are shown in [2] [3] .
Thickness error of the calibration fluid layer is 0.01 mm, measurement error of the sensor capacity, considering wires, with the values of the fluid layer thickness ≤2 mm, does not exceed 10−4 pF. If the thickness values in the calibrating fluid’s layer are greater, convective currents that increase the measurement error occur.
It is clear that the “dry” capacitance sensor has a maximum sensitivity in the range of medium and great thicknesses of the calibration fluid layer and the “drowned” capacitance sensor has a maximum sensitivity in the range of small thicknesses. It is clear that with the increase of the thickness of the calibration fluid layer in a “drowned” mode of measurements, the sensor capacity approaches the constant value.
To specify the behavior of variation curve of the “drowned” sensor at small calibration fluid layer thicknesses, the horizontal microscope MG-type was used as a reference device having finer upward movement adjustment of the measuring capillary 8 (see Figure 4). The interval of the MG-type microscope feed screw sensitivity (scale increment) in the vertical direction equals 0.002 mm within the capillary elevation range 2.5 mm. The measurements were performed at initial total compression of the bellows 6, and following movement of the microscope feed screw on way upward. The results of more accurate calibration of the capacitance sensor with reduced upward increment of measuring capillary 8 are shown in Figure 6. Thickness error of the calibration fluid layer is 0.002 mm, measurement error of the sensor capacity, considering wires, with the values of the fluid layer thickness ≤2.5 mm, does not exceed 10−4 pF.
The capacitance method for determination of the thickness of the fluid film (layer) in the channels shows high sensitivity, what can be proved with many examples.
In the simplest application of the plane capacitance sensor, condenser plates are arranged directly in the opposite side walls of the working section of the vertically oriented rectangular channel. Sensor plates are flush mounted with plane vertical side walls of the channel, which are parallel to the vertical moving film of the investigated fluid, and form closed plane condenser.
The sensitivity of that condenser, according to Alekseenko [11] , rises as the investigated fluid film with thickness h proceeds to cover the distance b between the condenser plates, and consequently, vapour (gas) gap b - h between the second condenser plate and external surface of the film decreases. The sensitivity value of the capacitance sensor is close to hyperbolic function and can be written as follows:
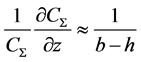 . (4)
. (4)
In the open-type capacitance sensor, where the curved electric field is concentrated in the area around the end portion surfaces of the measuring electrodes,
Figure 6. Calibration results for capacitance sensor in “drowned” state at small thicknesses of calibration fluid (water) layer.
the field density value and sensor sensitivity sharply reduce as the distance increases. Since two measuring end portion surfaces of the electrodes of the open sensor comprise electric charges of opposite sign, then together they form dipolar field, which density decreases proportionally to the cubed (degree 3) distance from the emitting surface of the electrodes [16] . This limits the long-range action of our capacitance sensor with open electrodes.
We performed the comparison of open capacitance sensor sensitivity, obtained in reliance on the empirical results of its calibration at small working fluid film thicknesses, with calculated value based on the hyperbolic function from the Equation (4), where the derivative value 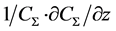 at zero film thickness was taken as equal to the experimental value. The comparison results are shown in Figure 7. It is seen, that for small film thicknesses up to 80 × 10−6 m (80 μm) the derivative value, obtained in reliance on the empirical results, are genuinely smaller and reduces more sharply in comparison with the hyperbolic function similar to (4). For fluid film thicknesses over 100 μm, in reliance on the empirical results, the open capacitance sensor sensitivity systematically exceed sensor sensitivity values obtained using the hyperbolic function similar to (4).
at zero film thickness was taken as equal to the experimental value. The comparison results are shown in Figure 7. It is seen, that for small film thicknesses up to 80 × 10−6 m (80 μm) the derivative value, obtained in reliance on the empirical results, are genuinely smaller and reduces more sharply in comparison with the hyperbolic function similar to (4). For fluid film thicknesses over 100 μm, in reliance on the empirical results, the open capacitance sensor sensitivity systematically exceed sensor sensitivity values obtained using the hyperbolic function similar to (4).
4. Capacitance Sensor: Temperature Measurement by Means of a Thermistor
The calibration of the CT3-19 thermistors was performed previously [31] [32] [33] [34] and all calibration measurements were performed in a stationary mode with an isothermal casing within the temperature range of 273.15 К - 473.15 К (0˚C - 200˚C). The calibration essence lied in the precise measuring of the thermistor resistance RC, Ohm, using the standard potentiometric method, in the stationary state and the set temperature T, K, that is determined according to the
Figure 7. The derivative of the calibration curve of the capacitance sensor for small fluid film thicknesses. 1―experimental results; 2―hyperbolic function similar to (4).
platinum resistance reference thermometer PRT-10. All temperature measurements were made at the gauge current value of 1 ma (1 × 10−3 A) and the emitted heat capacity is WPRT = (10 ÷ 17) × 10−6 W. The thermal capacity WC emitted by the gauge current on the thermistor is constant during all calibration tests and equals 20 × 10−6 W. We obtained a quartic polynomial equation [31] [32] [33] [34] that connected the temperature K and the logarithm of the thermistor resistance as follows:
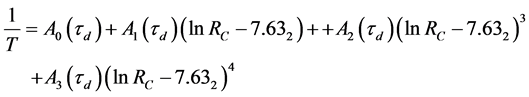 (5)
(5)
where 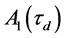 is the expansion coefficients with regard to the time drift τd; the minimum point of the distribution the derivative
is the expansion coefficients with regard to the time drift τd; the minimum point of the distribution the derivative 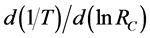 × 104, 1/К, as a function of the logarithm of the resistance of the thermistor lnRCmin = 7.632 ± 0.01, which corresponds the inflection point Tinf = 336.34 К (63.19˚C).
× 104, 1/К, as a function of the logarithm of the resistance of the thermistor lnRCmin = 7.632 ± 0.01, which corresponds the inflection point Tinf = 336.34 К (63.19˚C).
5. Measurement of the Heat Transfer Coefficient
Condensation zones of the HPs are provided with insulated thermocouples and set into the vortex continuous-flow calorimeter, shown in Figure 8, with stabilized water flow. To ensure accurate measuring of thermal power and heat removal augmentation in the HPs, jet flow of input water is swirled, values of flow velocity and vorticity due to air bubbles are recorded. The HPs evaporators, also
Figure 8. Vortical calorimeter. 1―vortical continuous-flow calorimeter; 2―heat pipes bolting flange; 3―glass cover; 4―cover fastening; 5―heat pipes; 6―resistance heater; 7―outlet stub tube for water flow; 8―inlet stub tube for water flow; 9― silicone sealant of the sensing wire; 10―capacitive sensors for measuring the thickness of the condensed layer of the working fluid; 11―the measuring and reference generators of the capacitive transducer; 12―external digital generator; 13―power assist element; 14―digital oscilloscope; 15―computer; 16―commutation switch; 17―digital voltmeter; 18―container for constant water head; 19―source of air bubble; 20―water flow meter; 21―va- cuum-jacketed zero temperature container.
equipped with thermocouples, is heated using a resistance heater, and the temperature is maintained at δТ˚C higher than the diethyl ether boiling temperature of 308.55 K (35.4˚C) under atmospheric pressure. The heater temperature is stabilized and HPs evaporator s overheat value is set in the range of δТ = 0 ÷ 20 К, herewith thermal power of single HP does not exceed 120 W.
Measurement were performed to disclose variability of the heat transfer coefficients in Laval-liked HPs and with standard cylindrical vapor channel.
The heat transfer coefficients in HPs, Faghri [35] is defined by the formula:

Temperature of evaporator surface and condensation surface of HPs were measured using differential thermocouples copper-constantan, heat power, transferred by condensations zones of HP to the calorimeter, was defined by the formula:

Input temperature of water at the calorimeter, temperature differences (heat value) of the flowing water at entrance and exit of the calorimeter were also measured using differential thermocouples copper-constantan, comparator Р3003 and digital voltmeter V7-34A. Water flow rate was measured using ultrasonic flowmeter. Total measuring inaccuracy of the thermal power E of the HPs does not exceed 1.7%.
Comparison of heat transfer coefficients in Laval-liked HPs and HPs with standard cylindrical vapour channel, with the equality of all dimensions showed following results, presented in Figure 9.
Figure 9. Comparison of heat transfer coefficients in Laval-liked HP and HP with standard cylindrical vapour channel. 1: Laval-liked HPs; 2: HPs with standard cylindrical vapour channel.
The increase of the heat transfer coefficient in the HP with a Laval-liked vapour channel appears to be related to the emergence of a vortex ring near the condensation surface of the HP.
Near the condensation surface of the Laval-liked HPs occurs vortex ring of the condensing vapour the estimated traffic pattern is shown in Figure 10.
Numerical Model Details
Numerical simulations of the vortex flows inside a vapour channel of the Laval-liked HPs have been performed in finite element modeling in CFD 10.0 code Fluent 6.3.26 under 2D, double precision axis-symmetric conditions. Navier-
Figure 10. The occurrence of a vortex ring near the condensation surface inside of Laval-liked HPs. The numerical analysis of flow in the Laval-liked HPs condensation zone shows that the vortex structure has a spatial nature, at the same time the flow asymmetry becomes apparent being determined by non-linear friction against the underlying surface and the two-dimensional compressibility of the wet condensing vapour as well. Figure 11 shows the results of numerical analysis of the distribution of the longitudinal component of the velocity of compressible moist vapour within the Laval-like HP. The formation of a vortex ring wet condensing vapour near the condensation surface inside of Laval-liked HPs leads to quite interesting results. Vortex ring is a highly gradient zone of the condensable moist vapour velocity with the opposite directions inside and outside the vortex ring. The numerical analysis of the velocity distribution along the centerline of the vapour channel in the Laval-liked HPs including the vortex ring shows the occurrence of two positive peaks of the velocity, one of them is in the critical section of the nozzle and the other near the condensation surface. In a critical section of the nozzle the axial component of velocity reaches 85 m/s, and near the condensation surface the counter-flow reaches the velocity of 33 m/s. The distribution of the axial component of velocity of the moist vapour shows the presence of a counter current due to the formation of a ring vortex within the vapor channel near the HPs condensation surface. This figure of the velocity distribution, shown in Figure 11, confirms the fact that the vortex ring is a zone of sharp velocity gradients, and as a consequence is also a pressure gradient. In the central part the vortex ring has a noticeable positive dynamic pressure, and it has a negative dynamic pressure in the peripheral part of the vortex ring. This means that lower static pressure occurs in the central part of the vortex ring and this leads to additional absorption of moist vapor in the condensation zone of Laval-liked HPs.
Figure 11. The distribution of the axial component of velocity of the moist vapour inside the vapour channel of Laval-liked HPs along the HPs centerline. Upper pattern with a positive velocity peak near the condensation surface of Laval-liked HPs represents the velocity distribution along the longitudinal axis of vapour channel and inside the vortex ring. The figure on the bottom with a negative velocity value peak near the surface of condensation represents the velocity distribution along the longitudinal axis and outside of a vortex ring and shows the presence of a counter current due to the formation of a ring vortex near the HPs condensation surface. Apparently, this means that the static pressure in the vortex center in the Laval-liked HP is less than the pressure in the axial part of the condensation zone of the HP with standard cylindrical vapor channel. The appearance of high static pressure in the peripheral part of the vortex ring, where there is a negative dynamic pressure leads to intensification of the condensation process near the top cap of the Laval-liked HPs, which leads, apparently, to an increased value of heat transfer coefficient in the Laval-liked HPs. This explains the reason why the heat transfer coefficient of Laval-like HPs becomes greater than HPs with the cylindrical vapor channel at boiling point in evaporator HP and there is formation of large amounts of vapor and increase in the efficiency of the nozzle in comparison with a cylindrical channel.
Stokes equations with measured boundary conditions were solved, i.e. using fixed temperature values of heat source and heat outlet. In the construction of the design model about 457233 finite elements were used, with increased meshing at injection capillary channels sections, nozzle throat section and turbulence element. Figure 10 shows a diagram of the vortex obtained by numerical simulation of CFD 10.0 code.
6. Measurement of Pulse Characteristics of HPs
The pulsation characteristics of HPs were measured in the following way [1] [30] . An overheating was imposed on the evaporator by δΤ = Т − ТB relative to the boiling temperature of diethyl ether at atmospheric pressure with the aid of resistive heater 6 and high-precision temperature controller increased in discrete steps of 1 K. Electrical pulses of 10 - 100 kHz and amplitude 5 V are applied to the electrodes of the capacitive sensor 10 (Figure 8). The modulation rate is measured via a gain and filtering circuit 13, whereupon the signal goes to measuring input of digital oscilloscope 14. The oscilloscope is connected to the computer 15 via USB-interface. Started from the specific overheating δTS = (Т − ТB) of HPs evaporator, electrical pulses become modulated. The modulation rate is measured using gain and filtering circuit 13, digital oscilloscope 14 and computer 15 and are shown in Figure 12 and Figure 13. Measuring inaccuracy of modulation rate does not exceed 3 - 5 Hz.
Initial pulsed flows occur in the Laval-liked HPs in the event of overheating of the evaporator δT ~9 K, frequency (modulation frequency of electromagnetic pulsation) is f1 ~386 Hz, (lower oscillogram); δT ~20 K f1 ~502 Hz, (upper oscillogram). The oscillograms without pulsations in the vapour channel of HPs do not have a low-frequency (400 - 500) Hz modulating features.
Table 1 shows the pulsation rate values (modulation rate), obtained in the Laval-liked HP, f1[Hz], and in the HP with standard cylindrical vapour channel, f2[Hz], depending on overheating δT, [K], of the evaporators.
While investigating HPs with standard cylindrical vapour channel and equal outer diameter 20 mm, length 100 mm and thickness of the evaporator and
Figure 12. Oscillograms of the increase of the modulation frequency depending on the thermal load on Laval-liked HPs.
Figure 13. Test values of modulation frequency depending on overheating δT = (Т − ТB) of HPs evaporator, with reference to the boiling temperature of diethyl ether 308.55 K (35.4˚C). 1 - HP with the Laval-liked vapour channel; 2 - HP with a standard cylindrical vapour channel. Both HPs have equal outer diameters 20 mm and equal sectional areas of capillary-porous inserts near the condensation region. As the overheating of the evaporator δT ~20 К increases, pulsation frequency in the Laval-liked nozzle goes up to ~502 Hz, derivative of the relationship between pulsation frequency and temperature is approximately 10.5 Hz/K.
Table 1. Pulsation rate values.
capillary-porous insert 3 mm, initial pulsed flows occur in event of overheating of the evaporator δT ~11 К, frequency (modulation frequency of electromagnetic pulsation) f ~406 Hz.
As the overheating of the evaporator δT ~20 К increases, pulsation frequency in the cylindrical vapour channel goes up to 474 Hz, derivative of the relationship between pulsation frequency and temperature is approximately 7.5 Hz/K.
The insensitivity zone of the capacity sensors in the cylindrical channel, defined by the initial convective nature of the vapour flow, is greater than in the vapour channel of Laval-liked HPs. Dynamic range of pulsations in the Laval-liked HPs vapour channel, is a little greater in frequency, in comparison to dynamic range of pulsations 406 Hz - 474 Hz in cylindrical vapour channel, and equals to 386 Hz - 502 Hz. Measuring inaccuracy does not exceeds 3 - 5 Hz.
6.1. Numerical Model Details
Numerical simulations of the vortex pulsation flows inside a vapour channel of the Laval-liked HP have been performed in finite element modeling in CFD 10.0 code Fluent 6.3.26 under 2D, double precision axi-symmetric conditions. Navier-Stokes equations with measured boundary conditions were solved, i.e. using fixed temperature values of heat source and heat outlet. The model was studied as a longitudinal section along the axes of the two injector channels, which helps to preserve all the specific features of whirling instability under the conditions of continuous circulation motion of the working fluid during liquid and vapour phases. In the construction of the design model about 457233 finite elements were used, with increased meshing at injection capillary channels sections, nozzle throat section and turbulence element. The model size is a compromise between available computer resources and computational investigation error.
Is clearly visible transition from stationary convective flow regime in the vapour channel to pulsatile flow regime. At high heat capacity, received by the HPs, and boiling in the grid evaporator, excessive vapour occurs in the convergent part of the nozzle, thus leads to pressure increase up to the value, at which the average temperature of layers of the flat grid evaporator becomes lower than the boiling temperature working fluid, and boiling in the evaporator stops. Excessive vapour spreads through the divergent part of the vapour channel to the cooled area of the HP and is partially condensed. Due to the condensation effect, the pressure in the vapour channel decreases and the boiling process in the flat evaporator proceeds. Pressure increase period, vapour wave spreading in the condensation area of the HP and return expansion wave define the pulsation period in the vapour channel.
6.2. Validation of Numerical Scheme
Evident conversion from convection mode to convection-vortex mode and then to pulsation mode of the vapour flow inside of the HP, is recorded at evaporator overheating value δT ~9 К.
Maximum value of velocity of diethyl ether moist vapour flow, obtained using calculation method in the throat section of the vapour channel using by the colour indication of the software CFD Design 10.0, reaches 100 - 110 m/s when pulsation occurs. This fact gives the opportunity to evaluate the Reynolds number Re of the vapour channel during pulsation, which is defined by the formula:

We substitute moist vapour density (vapour and drops) [17] [36] 
Duration of the pulsation period inside the divergent part of the HP vapour channel can be estimated using the formula:

Then substitute values of distance between pulsation crests (maximums) obtained in Figure 14 Δl ~(2 - 3) × 10−2 m, moist vapour flow velocity in divergent part of the vapour channel obtained using colour indication by the software CFD Design 10.0 uvp ~(20 - 30) m/s, and you will obtain numerical value of duration of the pulsation Δτ0 ~(0.75 - 1.5) × 10−3 s.
6.3. Analytical Evaluation
Evaporation cycle in HPs exist at low heat load of the evaporator, up to 4 - 6 W/cm2, and is characterized by convective flow in the vapour channel. Evaporation cycle of short HPs, when evaporator heating power is constant and maximum value is limited to prevent the development of bubble boiling in the flat grid evaporator, is defined in the following way:

Rate of evaporation of dry monomolecular vapour over the evaporator is defined by the following equation:

Mass flow of saturated dry monomolecular vapour over the evaporator is defined by the following equation:

Growth rate of the number of molecules of vapour over the evaporator in the convergent region of the nozzle of the vapour channel, which defines excess pressure over the evaporator and mass flow of vapour in HP, is calculated from the equation:
Figure 14. The results of flow simulation of compressible supersaturated vapour environment inside a vapour channel. The figure presents test values of the vapour flow pulsation in the vapour channel in the Laval-liked form of a HP, as overheating of HPs evaporator is increased in reference to boiling temperature of diethyl ether 308.55 K by 2 K; 5 K; 8 K; and 13 K, from left to the right.

Assuming approximately equal velocities and without considering the jet type nature of the flow pattern, the linear velocity of the hydrodynamic flotation of the vapour flow over the evaporator surface is calculated from the equation:

Insert expressions (5) and (4) in the Equation (3) to obtain the formula for calculation of molecular flow of the dry vapour over the evaporator:

Hydrodynamic flow of saturated dry vapour is defined by pressure difference value between the evaporator and condensation region in HP, according to the formula:

Equate mass and hydrodynamic flow of saturated dry vapour, and obtain the following equation:

Excess pressure over the evaporator defines transfer of the vapour flow in the vapour channel of the HP, and is calculated in linear approximation according to the equation:

With respect to the Clapeyron-Clausius equation, pressure derivative of the vapour by temperature is calculated in a conventional manner, nevertheless considering the fact that for liquid the specific volume ratio is small, 

Substitute expression (10) in (8), and obtain the equation to calculate vapour quantity in the HP:

Vapour temperature over the evaporator’s surface with low evaporation and without boiling is defined by the Equation (16):

Steady-state evaporation conditions in HP mean that the temperature in the evaporator does not exceed boiling temperature of the working fluid. Heating capacity of the HP, W, is defined according to the following equation:

Heat transfer coefficient at cross-section of the vapour channel of the HP is defined according to the following expression:

when the rate of heat supply into the thin evaporator is high, its average temperature is greater than the boiling temperature of the working fluid during bubble boiling or vapourization. The hydrodynamic vapour flow at the converging region of the nozzle has no time to carry out heating capacity generated through boiling in the evaporator.
Vapour density and pressure increase and boiling temperature of the working fluid goes up until it exceeds average temperature of the evaporator. Upon pressure increase the boiling in the evaporator stops (slows), and an overpressure wave spreads in the vapour channel to the condensation region of the HP, where the vapour becomes supersaturated, and condenses. The condensation process is not instant, and when the evaporator’s activity is slowed (stopped), condensation lasts until the pressure decreases to the vapour saturation pressure at the condensation temperature, thereafter the condensation process stops.
The slow process of saturated vapour pressure decrease, due to condensation, feeds back through the vapour channel of the HP back to the evaporator, and the boiling process there is resumed.
Pressure pulsations in the vapour channel of the HP result from boiling and intensive vapour generation in the evaporator, non-instantaneous mass-transfer through the vapour channel to the condensation region of the HP, and the slow condensation process, which provides pressure decrease in the condensation region at first and then in the evaporator of the HP.
Following all described processes the next pulsed evaporation cycle is resumed. The heating capacity, entering to the flat grid evaporator of the short HP, when the evaporator’s temperature exceeds the boiling temperature TB(p) of the working fluid, is defined according to the next equation:

It is considered that moist vapour is formed of two subsystems: microdrops system and dry vapour system. Rate of vaporization of the moist droplet vapour flow is defined in the standard way:

For the purpose of simplification of the analytical model construction, the real droplet vapour flow over the evaporator - having microdrops dimensioned by complicated double-humped distribution function, Lee, Reges, Almenas, [37] is reported in terms of a mono-dispersal system of spherical microdrops with arithmetic middling radius ra, which is frequently used while analyzing two- phase droplet vapour flows:

Considering the accepted assumption over spherical shape of microdrops, the expression for absolute moisture of the droplet vapour flow:

the density of moisture vapour without taking into account the relative motion phases

Synergies between consumable and absolute mass concentrations of microdrops or consumable and absolute moisture are defined according to the following relation:

The value γG represents the relation between quantity of the condensed droplet phase and total quantity of the two-phase droplet vapour, and, considering the expression (22) is as follows:

Mass flow rate of microdrops on the evaporator’s surface are considered to be proportional to vaporization velocity and mass flow rate of the vapour:

To evaluate the vapour quantity transported from the evaporator to the condensation region of the HP, Equation (31) is used, where the microdrops subsystem contribution to the generation of overpressure of the two-phase droplet mixture over the evaporator P(Tev) in the vapour channel is neglected:

As a result of the boiling process in the evaporator, the pressure of the vapour over the evaporator increases up to P*, whereby the boiling process in the surface layers and further in the whole of the thin evaporator (3 mm thick) is slowed (stopped) due to the fact that average temperature of the evaporator Tev becomes lower than the boiling temperature of the working fluid in the evaporator under the increased pressure and the confined spaces:

Furthermore, pulsing of the overpressured vapour begins to spread to the condensation region through the vapour channel. Cessation of boiling and retarding of vaporization in the evaporator of the HP lead to significant reduction (cessation) of the heat release and decrease in moist vapour transportation along the vapour channel of the HP to the condensation region of the HP. The time period Δτev of pressure increase up to P* and cessation of boiling in the capillary-porous evaporator is estimated in linear approximation in ideal gas state and laminar heat transfer inside of the vapour channel of the HP, according to the formula:

Surplus energy (increased pressure) release time in the evaporating region, by means of vapour flow transfer to the condensation region of the HP, is estimated according to the following formula:

Surplus pressure release time ΔτHP partially determines the time value of oscillations of the vapour flow in the vapour channel of the HP, during which the vapour pressure pulse, initiated over the evaporator, reaches the HP condensation surface, and condenses partially. The time period Δτcond of pressure decrease up to P(Tcond) is estimated according to the formula:

As a result of the liquid phase formation, pressure near the cooling condensation surface reduces to:

This leads to the slowing of heat transfer through the vapour channel, the rarefaction wave propagation from the condensation zone to the evaporator and the start of the next cycle of pulsed increase of the pressure near the evaporator’s surface. Thus, cycle pulse duration Δτ0 in the vapour channel of the HP:

The analysis of the obtained measured data of heat transfer over the evaporator shows that the designed HPs work in the boiling mode. This fact is confirmed by influences of operating parameters of the vaporization process (heat flow density q and pressure P(Tev)) on the heat transfer coefficient α. The influence of these parameters is related to the similar influence of heat flow density and pressure over the bubble boiling in the substantial volume. Performed numerical estimation of parts of pulsation duration Δτ0 from the expression (38) shows the following.
Pressure increase duration Δτev over the HP evaporator leads to increased values Δτev ~10−1 - 10−2 c, which means incomplete adequate flat model for estimation of evaporability in the evaporator. It is necessary to consider nonequilibrium volumetric vapourization with regard to the structure and porosity of the evaporator, temperature and moisture gradient in the boiling two-phase working fluid.
Moving duration ΔτHP of the vapour cluster along the convergent-divergent HP vapour channel at vapour flow velocity in the channel equal ~100 m/s ÷ 300 m/s, reaches ΔτHP ~(4.8 ÷ 1.6) × 10−3 s, which is acceptable only in the case when sonic velocity in dry vapour is ~300 m/s and correspondingly large temperature gradients in the vapour channel.
Maximum duration of condensation period of moist vapour is also excessive and reaches Δτcond ~10−1 - 10−2 s
Duration of expansion wave motion from condensation region to the HP evaporator at sonic speed in moist vapour about 100 m/s, doesn’t exceed Δτsound ~1 × 10−3 s.
Comparison of experimental measured results of pulsation period duration in the convergent-divergent vapour channel of short low temperature HPs Δτ0 = (2 ÷ 2.5) × 10−3 s with the valued Δτ0 ~(0.75 ? 1.5) × 10−3 s obtained using numerical method and the software CFD Design 10.0, shows that they have good fit values.
Comparison of experimental measured results of pulsation period duration in the convergent-divergent vapour channel of short low temperature HPs Δτ0 = (2 ÷ 2.5) × 10−3 with estimated values obtained using analytical method, shows excessive values of analytical results. Suggested simple theoretical model of the flat surface evaporation gives excessive values of pulsation period duration and is not fully correspond to acutely nonequilibrium evaporation processes in the grid capillary porous evaporator with boiling working fluid.
7. Capacitance Sensor: Transducer Calibration
To perform measurements of the thickness of the liquid condensate layer inside of the HP we used the method of detection of electrical capacity ΔС changes of capacitive sensor as the thickness of the liquid condensate on its surface changes. Due to small values of sensor capacity variations in the event of film condensation of the vapour inside of the HP, the thickness of the formed condensate of the working fluid was defined by measuring the difference of two frequencies of the measuring and reference high-frequency generators, which together constitute the main part of the capacitance transducer. Using modern imported hardware components, the transducer of capacity change―differential frequency― fluid film thickness at the condensation surface, was made combined with the measuring and reference capacitance sensors, and arranged under constant temperature in the vortical continuous-flow calorimeter (Figure 8). The transducer comprises two identical high-frequency generators, mixer and low-frequency filter. As the result, at the transducer output low-frequency signal can be obtained, which represents the difference between signals of the reference and measuring generators, and appears to be proportional to capacity change of the open capacitance sensor as the thickness of the liquid condensate on its surface changes. Using calibration dependencies, the difference between signals of the reference and measuring generators can be transformed in the thickness of the condensate film of the working fluid.
Variating capacity of the open capacitance sensor, in the event of film condensation of the vapour inside of the main HP, is included in the oscillating counter of the measuring alternating current generator ~33 МHz, and changes its frequency. Identical capacitive sensor of the reference HP, filled with noncondensable air, is included in the oscillating counter of the reference generator of the capacitance transducer. The main HP, called measuring, is filled with diethyl ether and the reference one, which is completely identical to the main pipe, is filled with dehumidified air with dew point temperature lower than 233.15 К (−40˚С).
To increase the measurement accuracy of the difference between signals of the reference and measuring generators, both of them have the same circuit design, arranged on similar circular printed-circuit boards 0.3 mm thick directly on the flat top covers of the HP. Boards diameter equals HP diameter 20 mm, 0.02 mm thick insulating fluoroplastic films are interlaid between boards and covers. Boards are pressed to the surfaces of HP top covers and securely fixed using short wire leads of capacitance and microthermistor sensors sealed into them. Hence, it is possible to minimize all stray capacities of the electric installation and wired-logic connections. Microcircuits, radioelements and printed circuitry are coated with several layers of the insulation compound based on lacquer UR-231.
Boards, along their perimeter, are surrounded by cylindrical copper cases, having 20.5 mm diameter, 7 mm highness and 0.25 mm wall thickness, welded directly to the HP, and hermetically closed with covers in such a way as to implement the modular structure for each of the two high-frequency generators with the isolation from the external high-frequency interference (noise) and water in the continuous-flow calorimeter. The special focus was on the selection of wires, in the capacity of which imported sealed wires with polymeric insulation were used, including shielded wires.
All supply wires, with polymeric insulation, including current and sensing wires of thermistors, generators and thermocouples are hermetically inserted in the calorimeter and glued to the surface of copper covers of protective cases, where they take on the water temperature in the continuous-flow calorimeter. Further, wires are inserted in the openings, made in cases covers, and welded to the generators boards. Welding joints and wires ends are coated with several layers of the insulation compound based on lacquer UR-231 There is the provided possibility of warping the reference capacity of the reference generator, without loss of sealing of copper protective cases. The process of heat removal from heat-dissipating elements of generators is caused by the natural convection; the temperature of sealed copper protective cases equals the water temperature in the vortical continuous-flow calorimeter.
Upper parts of both HPs are placed in the vortical continuous-flow calorimeter (see Figure 8), in which the input temperature and water flow rate are stabilized with the adjustment thermostat, T = 298 ± 0.03 K; G = 0.13 g/s. Using the resistive heater BRT-3, the HPs evaporators are maintained at the temperature, which exceeds the boiling temperature of diethyl ether by the overheating value of δТ = Т − ТB = 0 ÷ 20 К, herewith, the thermal power of the HP, filled with diethyl ether, doesn’t exceed 120 W.
Both high-frequency measuring and reference generators are made on two similar broadband amplifiers EL4551 (INTERSIL), which provide amplification of signals up to 90 МHz. The circuit of each generator is arranged on the LC series oscillating circuit, parallel to its capacity the measuring and reference capacitance sensors are connected, which are installed in the measuring and reference HP.
Generators circuits are identical, excluding small tuning capacity (varicap), disposed on the reference generator, thus under the influence of disturbing factors, the behavior and value of frequency variation in both generators can be reputed as approximately equal. At the generators output high-frequency operational amplifiers are positioned, which offer the possibility to perform appropriate adjustment and signal matching. The measuring and reference signals are sent from amplifiers outputs to balance mixer inputs ADE-1 type. The mixer represents diode bridge with standard performance and center-tap toroidal transformers, arranged on the separate board in the continuous-flow calorimeter under constant temperature. The board, along its perimeter, is also surrounded by cylindrical copper case, 9 mm highness and 0.5 mm wall thickness, and hermetically closed with the cover to provide the isolation from high-frequency interference (noise) and water in the continuous-flow calorimeter.
Processes of hermetic insertion in the calorimeter, gluing the wires on the case cover, insertion and sealing of cover openings and welding the wires to the mixer board are identical with the previously mentioned procedure for high-frequency generators.
At the mixer output we obtain signals with frequencies equal to the sum and difference of input signals frequencies of reference and measuring generators f = f1 ± f2. In the addition to the mentioned, in the output spectrum there are spurious signals with other frequencies, caused by transformation distortions. Through the amplifier the signal goes from the mixer output to the low-frequency filter (LF filter), where the signal of the input frequencies difference is extracted. Capacitance transducer layout is shown in Figure 15.
Further transformation of differential frequency signals, which is the measure of detuning the generators, related to the formation of the condensate film of the working fluid at the measuring surface of the capacitance sensor, is performed on the PC-connected digital oscilloscope AKIP Tektronix, which provides the means to complete all necessary mathematical operations with signals and
Figure 15. Circuit of the capacitance transducer consisting of a gauging generator and a reference generator, a mixer and a low frequencies filter, with a temperature-measuring circuit using two thermistors, a USB-Relay switchboard, a voltmeter AKIP B7-78, a PC and a digital oscilloscope AKIP Tektronix.
perform two-channel measurements with sampling frequency up to 1 GHz with high accuracy.
Further transformation of differential frequency signals, which is the measure of detuning the generators, related to the formation of the condensate film of the working fluid at the measuring surface of the capacitance sensor, is performed on the PC-connected digital oscilloscope AKIP Tektronix, which provides the means to complete all necessary mathematical operations with signals and perform two-channel measurements with sampling frequency up to 1 GHz with high accuracy.
The temperature in the measuring and reference HP is defined using two thermistors according to the potentiometric circuit, circuital current is measured using standard resistance coil R 321 accuracy class 0.01, disposed in the passive thermostat at room temperature. The set of “Backen” batteries in ground metal case serves as the current source. Another measuring element is the PC-con- nected digital voltmeter AKIP B7-78 or voltage comparator R3003 with increment of 0.01 μV, herewith, the thermal power WC evolved at each thermistor is the same as during calibration.
The temperature data input in the common computer bus is realized using the measurement module E14-440.
To increase the measurement accuracy of temperature (temperature differences), when measuring with the thermistor, thermistor signals are subject to the filtration of direct component voltages using calibration signals obtained using the comparator R3003. After subtracting the most significant digits, the variable components are supplied to the four digit AD converter E14-440 and then to the computer. Further, when calculating the temperature, significant digits (the constant component) are added using software-based method.
The measurement results are recorded in the computer as the data array of logarithms of thermistors resistances and temperature.
To perform measurement comparison and control, the signals of the reference and measuring generators, mixer and low-frequency filter signal are connected to the external outputs and can be connected to the measuring devices (amplifier, oscilloscope, frequency meter, alternating current bridge, spectrum analyzer, selective voltmeter, etc.), disposed on the mounting rack adjacent to the measuring and reference HPs, arranged in the calorimeter. To increase the measurement accuracy of condensate film thickness inside of the HP and except all errors associated with the intermediate transformations like film thickness―sensor capacity changing, and sensor capacity changing―difference frequency of generators, the calibration of the entire capacitance transducer as one element was performed, using the HP segment, shown in Figure 4. On the external surface of the cover 2 (see Figure 4), the second measuring generator was assembled, identical to the first one, and likewise, is coated with insulation compound and enclosed in the isolating copper case with the hermetic cover. The case is 7 mm high and has 0.25 mm thick walls, and is also closed with the isolating cover.
The input and output of the flowing water from the external stabilized thermostat 18, shown in Figure 8, was arranged in the internal cavity of the extended stabilizing sheath 5 (Figure 4), and heat-exchange conditions on the surface of the second measuring generator on the HP segment cover were identical to the heat-exchange of the first measuring generator in the vortical continuous-flow calorimeter (Figure 8). The water flow was also drawn through the stabilizing sheath 5 (Figure 4), from the external stabilized thermostat 18, shown in Figure 8. In the internal cavity and in the stabilizing sheath itself the temperature of the flowing water was 298 ± 0.03 K. As the reference generator was used the standard reference generator, shown in Figure 8, disposed on the reference HP filled with dry air. The experimental data arrays of differential frequency and layer thickness of the calibration fluid on the capacitance sensor surface inside the HP fragment 3 (Figure 4), for three fluid variants were made in accordance with the measurement results of the frequency difference between signals of the second measuring and first reference generators. Results for calibration of the second measuring generator are shown in Figure 16. The measurement error of frequency differences was less than 0.2 kHz, layer thickness error of the calibration fluid in the interval 0 - 2.5 mm and the use of the microscope was 0.002 mm.
The attainment of the saturation in measurements of frequency differences is related to the event, that the calibration fluid thickness begins to exceed the penetration depth of the electric field of the capacitance sensor. Starting with the fluid layer thickness of h = 2 mm, which is equal to the distance between
Figure 16. Calibration curves demonstrating the differences between frequencies of the gauging and reference high-frequency generators, depending on the thickness of the working fluids’ layer: 1 ? water H2O; 2 ? ethyl alcohol C2H5OH; 3 ? diethyl ether C4H10O. The calibration curves for frequency differences of the measuring and reference generators attain the saturation, for water case it is ~248 kHz, ethanol ~157 kHz, diethyl ether ~130 kHz.
electrodes a, the frequency differences growth sharply reduces, but once the layer thickness reaches h = 3.5 mm, the growth virtually recedes down to zero. It means that the capacitance sensor and as a consequence the frequency differences of the generators is insensitive within this thickness range of the fluid layer and defines a transition to the saturation state wherein the resolution decreases. The transition to the saturation state is caused by the closure of the electric field within the penetration (distribution) depth of the field Λ ~3.5 mm and by a virtual absence of the field beyond this depth Λ. The values of these saturation frequencies, when using different working fluids, is defined by fluid permittivity 


It is clearly seen, that the slope of the obtained calibration curves, defined by the sensitivity of the capacitance transducer, depends on the permittivity of the used working fluids. The sensitivity of our equipment is maximum in case of water use, (dΔf/dh) ~160 kHz/mm, less in case of ethanol use (dΔf/dh) ~118 kHz/mm, and lesser in case of diethyl ether use (dΔf/dh) ~100 kHz/mm. Performed estimates show that the operation rate of our capacitance transducer is not less than 103 Hz and its response time does not exceed 10−3 s.
8. Capacitance Sensor: Conduct of Measurements
Once the equipment is warmed up, the generators are turned on and a temperature balance of thermistors is reached in the gauging and support HPs, the reference generator frequency is aligned with the gauging generator frequency. Prior to turning on the condensers’ heating and HP starting to operate, the frequencies’ difference is set to close to zero and the gauging generator frequency is always smaller than the reference generator frequency by a small amount of 0.2 kHz. Later, when the condensate film forms, the gauging generator frequency decreases, while the frequencies’ difference increases and does not reverse its sign. The temperature difference between two thermistors in balance does not exceed 1 × 10−3 K. The program that runs the capacitance transducer has two operating modes: “control” and “measuring”. In the “control” mode, a circular scanning of all sensors, including thermocouples, thermistors and capacitance sensors, is performed and measurement outcomes are processed and displayed on the screen. In this mode, such parameters of the managing program as the duration of the sensors scanning cycle, measurement times for digital voltmeters, oscilloscope, frequency meter, etc., are adjusted. After the HPs condensers and the vortex flow calorimeter reach steady isothermal states, the program switches to the “measuring” mode. In this mode, the difference between the reference generator frequencies and the decreased gauging generator frequency, the temperature of thermistors and thermocouples, and heat-transfer properties of HP are measured, the outcomes are processed, the average, max. and min. values of the film thickness and temperature are calculated and displayed on the screen. Obtained arrays of experimental data are maintained and a measurement library is formed.
Despite the thermostabilization of the gauging and reference generators in the flow calorimeter with water at a constant temperature, the minimal length of wiring, the minute shielding and the temperature control of all wires, the difference frequency Δf of the generators slowly drifts by approximately 0.2 kHz when conducting the measurements. This drift determines the smallest value of the capacitance change ~3 × 10−6 pF our equipment is able to measure. In our measurements, frequency dependences of the dielectric permeability of diethyl ether are low and the dielectric loss tangent at frequencies ~30 MHz does not exceed 10−2 [16] .
Measurement outcomes for the time-averaged values of the diethyl ether layer thickness on the smooth condensation surface inside HP depending on the heat load on the condenser are shown in Figure 17. A non-linear and sharply decreasing dependence of the thickness of the liquid condensate film on the HP condenser’s overheating is obtained, while the absolute error of the thickness measuring does not exceed 2 × 10−3 mm.
The typical experimental dispersion of measurements of the average values of the condensate film thickness ~2 × 10−3 mm noticeably increases starting the overheating value δT ~(11 ÷ 12) К, when a boiling process starts in the capillary porous HP evaporator and the vapour becomes humid.
8.1. Capacitance Sensor: Conduct of Measurements: Swirling Flow
Swirling flow occurs in many engineering applications, such as vortex chambers,
Figure 17. Dependence of averaged values of the diethyl ether layer thickness on the condensation surface on the HP condenser overheating in reference to the boiling temperature of diethyl ether δT = T ? TB, K, at a semi-logarithmic scale.
separators, pumps, gas turbines, and so on. In all cases swirl is used to produce good mixing, improve the flow stability and to increase the condensation process in the pipes, experimental confirmation of this fact is given in many publications [38] [39] [40] [41] .
In all confined vortex applications it is important to understand adequately the overall swirling flow field evolution as a function of both the geometrical and flow parameters. In metal HPs the control of the vapour swirling flow parameters is indirect and appears by the pulsating of the rotation flow of the working fluid film on the condensing surface.
Time-averaging of the empirically obtained instantaneous values of the diethyl ether film thickness on the condensation surface becomes necessary due to the fact that vapour flow inside the vapour channel of HP has a clearly precessing jet nature. In the capillary porous condenser, 4 injector channels are arranged along its entire thickness and symmetrically with respect to the longitudinal axis of HP (see Figure 3). The channels are arranged on a circumference that is located inside a critical nozzle diameter of the HP vapour channel and tilted at 25˚ in tangential direction. The channels’ diameters augment and equal to 1 mm, 1.1 mm, 1.2 mm and 1.3 mm. Diethyl ether evaporation in these tilted capillary channels forms a steady jet flow above the condenser surface and a swirl of the entire vapour flow in the HP steam channel. In addition, the difference between the injector channels’ diameters leads to a precessing of the vapour jet flow and a formation of a rotating spiral-shaped vapour swirl, shown in Figure 18. This precessing is manifested in the occurrence of a pulsating rotating flow of the fluid
Figure 18. The jet flow above the tilted injector channels with augmentative diameters made in the capillary porous condenser leads to a swirl formation and precessing of the velocity of diethyl ether vapour flow in the vapour channel of short HP. The flow velocity is stated in m/s.
film on the HP condensation surface.
The vapour flow velocity was calculated using CFD Design 10.0 program and an improved k − ε model [42] was implemented for the turbulence consideration. Due to a more detailed description of the turbulence dissipation velocity, the abovementioned model ensures a higher precision of the turbulent viscosity calculation as compared to a standard k − ε model.
It proves significant when modelling complex swirling turbulent flows and flows with a great streamline curvature that are similar to those existing inside the short HPs’ steam channel that is executed in a form of a nozzle similar to the de Laval nozzle.
Because of the existence of a relative movement of phases, the fluid film on the condensation surface, HP is engaged in a rotational movement due to the shearing stress τw that exists between the outer film surface and the swirled precessing flow of condensing vapour.
The damped precessing of the jet vapour flow velocity and the rotational irregularity of condensation related to the precessing lead to a formation of additional shearing and normal stresses on the film surface and, consequently, to a formation of irregularity (crest) of the film thickness. The rotation rate of this irregularity of thickness and temperature of the diethyl ether film does not exceed (10 ÷ 11) Hz and was securely recorded by our capacitance transducer. Rotation of the irregularity on the film surface is recorded (perceived) by the capacitance transducer as pulses of the film thickness, while the pulsing rate rises as the HP condenser’s overheating increases. Thickness, temperature and flow velocity of the diethyl ether film on the condensation surface are inconsistent both due to the swirled jet flow and related irregular spatial vapour condensation and due to the jets precessing in the HP steam channel and rotational irregularity condensation, which is supported by calculations and measurements effected using a capacitance transducer. Calculation outcomes for the tangential component of the film flow velocity that are executed using CFD Design 10.0 program are shown in Figure 19.
The narrow areas of lower velocity values as highlighted in the radial direction in Figure 19 divide the flow field into sectors that are determined by the swirled jet flow of vapour near the condensation surface.
In the right part of the illustration, between two contour lines, the colour highlights a major velocity singularity determined by the precessing of vapour jet flow. Outer and inner contour lines P(1) and P(2) are drawn in such a way that the gauging capacitance sensor is located between them in the right part of the illustration, while the microthermistor is located in its left part. Figure 19 and Figure 20 demonstrate estimated values of the tangential component of
Figure 19. Estimated values of tangential component field for the flow velocity Vφ of the diethyl ether film on the smooth condensation surface inside HP.
Figure 20. Estimated values of tangential component field for the flow velocity Vφ of the diethyl ether film on the smooth condensation surface along the contour lines P(1) и P(2) from Figure 19. The upper graph in red is a tangential component of velocity achieved along the inner contour line P(2) and the lower graph is a tangential component of the film flow velocity along the outer contour line P(1).
velocity Vφ of the diethyl ether film on the smooth condensation surface and film temperature along contour lines P(1) and P(2).
Overheating of the evaporator in reference to the boiling temperature of diethyl ether at atmospheric pressure is 15 K, the temperature difference between the evaporator and the condensation surface is equal to 25 K. Velocity maximum of pulsations reaches 0.3 m/s.
Calculation outcomes shown in Figure 20 and Figure 21 demonstrate a clearly expressed and related to the precessing of vapour jet flow pulsing change of both the tangential component of flow velocity Vφ of the diethyl ether film on the condensation surface HP and the film temperature along the contour lines P(1) and P(2). Figure 22 and Figure 23 show oscillograms of the change in thickness (capacitance) and temperature of the diethyl ether film on the condensation surface inside HP that are obtained using a capacitance transducer and a micro thermistor CT3-19.
One can clearly see the recurring singularity (crest) on the film surface that is formed by the precessing vapour jet flow and recorded by the capacitance transducer as a film thickness pulsation. It proves an existence of a precessing swirled flow in the steam channel of HP that leads to a rotational inconsistency
Figure 21. Estimated values of pulsations of the diethyl ether film temperature on the condensation surface along the contour lines P(1) and P(2) from Figure 19. The upper graph in red is temperature distribution along the inner contour line P(2) and the lower graph is temperature distribution along the outer contour line P(1). The amplitude of the temperature pulsations reaches 6 K, overheating of the evaporator relative to the boiling temperature of diethyl ether at atmospheric pressure is 15 K, the temperature difference between the evaporator and the condensation surface is equal to 25 K.
Figure 22. Oscillograms of thickness pulsations for the diethyl ether film on the gauging capacitance sensor’s surface that coincides with the smooth condensation surface of HP. Overheating of the evaporator relative to the boiling temperature of diethyl ether is (15.45 ± 0.01) K. Temperature difference between the evaporator and the outer surface of the HP cover in the calorimeter is (25.13 ± 0.03) K.
Figure 23. Oscillograms of the measured with micro-thermistor temperature pulsations for the diethyl ether film on the condensation surface inside HP. Overheating of the evaporator relative to the boiling temperature of diethyl ether is (15.45 ± 0.01) K. Temperature difference between the evaporator and the outer surface of the HP flat upper lid in the calorimeter is (25.13 ± 0.03) K.
of vapour condensation and to an emergence of a rotating singularity (crest) on the diethyl ether film surface on the condensation surface of HP. The singularity (crest) nature is complex, the thickness of the actual crest reaches ~0.0005 mm, and the duration is ~0.014 s. The film thickness pulsation swing reaches 0.0023 mm.
The film temperature change is regular and leveled, the duration of temperature pulsation periods coincides with the duration of film thickness pulsation periods, which additionally supports the rotational nature of the film flow. Complete swing of the film temperature pulsations on the HP condensation surface reaches 5.12 K and it can be claimed that precessing of the vapour jet flow is taking place in the HP vapour channel and the temperature of the vapour jets differs.
It should be noted that oscillograms of pulsations of the diethyl ether film thickness on the smooth condensation surface (see Figure 22) is similar to the ones of temperature pulsations of this film that is obtained using a micro thermistor (see Figure 23), which may be related to the recurrence of the condensation process. Frequencies that have been determined on the grounds of pulsations of the film thickness and temperature are the same and equal to fpuls = 10.34 ±0.03 Hz. It is worth mentioning that the performed estimation of the average value of tangential component of the film flow velocity above the capacitance sensor’s surface, judging by the experimental value of the pulsations frequency fpuls ~10.34 Hz is close to the estimate values shown in Figure 19 and Figure 20:

In order to evaluate the impact a swirling precessing vapour jet flow in a steam channel of short HPs has on the rotational flow of the diethyl ether film on the condensation surface, a similar HPs was manufactured with an identical steam channel and an identical capillary porous evaporator and capillary-porous insert, but without tilted injector capillary channels.
Measurement outcomes for the thickness and temperature of the diethyl ether film on the condensation surface are shown in Figure 24 and Figure 25 without tilted injector capillary channels in the evaporator and without swirling and precessing of the vapour flow in the vapour channel.
There are no clearly expressed recurring rotational flows on the condensation surface inside HP. All measurements of the thickness of the condensing diethyl ether film were performed in a HP’s vertical position; condensation occurred on the horizontal inner surface of the upper lid and the gravity force projection on the film movement direction is zero.
Overheating of the evaporator relative to the boiling temperature of diethyl ether is (15.17 ± 0.01) K.
Temperature difference between the evaporator and the outer surface of the HP flat upper lid in the calorimeter is (25.47 ± 0.03) K. There are no rotational flows on the condensation surface inside HP. Value of the film thickness pulsations does not exceed 0.002 mm.
In our case, the film movement is determined by a dynamic impact of a condensing vapour flow that moves in a radial and a tangential (circular) directions along the outer surface of the film. As a first approximation, the vapour pressure can be deemed constant and the film movement is caused solely by shearing stresses τwr and τwφ that affect the film’s outer surface.
Figure 24. Oscillogram of the diethyl ether film thickness on the gauging capacitance sensor’s surface that coincides with the condensation surface of a short HP, with a condenser, without tilted injector capillary channels and without swirling and precessing of the vapour flow in the steam channel.
Figure 25. Oscillogram of the diethyl ether film temperature, measured with micro- thermistor on the gauging surface of the capacitance sensor that coincides with the condensation surface in a short HP, with the evaporator, without tilted injector capillary channels and without swirling and precessing of the vapour flow in the steam channel.
Overheating of the evaporator relative to the boiling temperature of diethyl ether is (15.17 ± 0.01) K Temperature difference between the evaporator and the outer surface of the HP flat upper lid in the calorimeter is (25.47 ± 0.03) K. The film temperature pulsation value does not exceed 1 K. The diethyl ether film thickness was averaged out on time intervals greater than the rotational pulsations period 0.1 s. The film thickness is constant at the averaging period over 0.1 s with a preset overheating of HP evaporator due to the existence of a stationary process of diethyl ether transferring (absorption) into a capillary porous insert placed along the perimeter of the HP upper lid (Figure 3) and the fluid’s return to the evaporator.
The heat resistance of the diethyl ether film on the condensation surface inside HP can be estimated in a standard way according to the following formula:

The overall heat resistance of a short HP that is determined using a vortex flow calorimeter in Figure 8 with the evaporator overheating δT = T ? TB =20 K decreases down to ~0.4 K/W. It means that contribution of the condensate film δ ~10−2 mm thick into the overall heat resistance of HP is ~60%. Obtained results enable to determine the true thickness, temperature, rotation frequency, pulsation values for the film thickness and temperature on the condensation surface inside HPs. Subsequent study results and a detailed analysis of the film flow on the condensation surface and inside low-temperature HPs will be presented in the future written works.
8.2. Conclusions
1. Capacitance method may be applied for measuring instantaneous and average (time averaged) values of thickness of the diethyl ether film on the condensation surface in short low-temperature range metal HPs.
2. Using the capacitive sensor we detected that thickness of the working fluid condensate film in short low-temperature HPs decreases with an increase of the condenser overheating. We have achieved a non-linear dependence of the liquid condensate film thickness on the HP condenser overheating, while the absolute error of thickness measurement does not exceed 2 × 10−3 mm.
3. Using the capacitive sensor is first detected rotating pulsating flow on the condensation surface inside HPs. The frequency of rotation is equal to 10.34 ± 0.03 Hz.
Cite this paper
Seryakov, A.V. (2017) The Study of Condensation Processes in the Low-Temperature Short Heat Pipes with a Nozzle-Shaped Vapour Channel. Engineering, 9, 190-240. https://doi.org/10.4236/eng.2017.92010
References
- 1. Seryakov, A.V. (2014) Pulsation Flow in the Vapour Channel of Short Low Temperature Range Heat Pipes. International Journal on Heat and Mass Transfer Theory and Application, 2, 40-49.
- 2. Seryakov, A.V., Ananiev, V.I. and Orlov, A.V. (2015) Condensation Research in the Short Low-Temperature Range Heat Pipes. Proceedings of the 9th Minsk International Seminar of Heat Pipes, Heat Pumps, Refrigerators, Power Sources, Minsk, Belarus, 7-10 September 2015, 168-176.
- 3. Seryakov, A.V. and Ananiev, V.I. (2015) Condensation Research in the Short Low-Temperature Range Heat Pipes. Proceedings of the VIII International Symposium on Turbulence, Heat and Mass Transfer, Sarajevo, Bosnia and Herzegovina, 15-18 September 2015, 693-696.
- 4. Seryakov, A.V. and Konkin, A.V. (2015) Numerical Simulation of Pulsations in Vapour Channel of Low-Temperature Range Heat Pipes. Proceedings of the 8th International Symposium on Turbulence, Heat and Mass Transfer, Sarajevo, Bosnia and Herzegovina, 15-18 September 2015, 677-680.
- 5. Ducler, E. and Bergelin, O.P. (1952) Characteristics of Flow in Falling Liquid Films. Chemical Engineering Progress, 48, 557-570.
- 6. Rogovaya, А., Olevsky, V.М. and Rinova, N.S. (1968) Measuring Thickness and Profiles of Fluid Film. Experiment Devices and Technique, No. 1, 189-192.
- 7. Ozgu, M.R., Chen, J.C. and Eberhardt, N. (1973) A Capacitance Method for Measurement of Film Thickness in Two-Phase Flow. Review of Scientific Instruments, 44, 1714-1716.
https://doi.org/10.1063/1.1686039 - 8. Thorncroft, G.E. and Klausner, J.F. (1997) A Capacitance Sensor for Two-Phase Fluid Film Thickness Measurements in a Square Duct. Journal of Fluids Engineering, 119, 164-169.
https://doi.org/10.1115/1.2819103 - 9. Krotov, S.V., Nazarov, А.D., Pavlenko, А.N., Pecherkin, N.I., Serov, А.F. and Chekhovich, V.Y. (1997) Capacitance Gauge of Local Thickness of Fluid Film. Experiment Devices and Technique, No. 1, 149-152.
- 10. Alekseenko, S.V., Nazarov, А.D., Pavlenko, А.N., Serov, А.F. and Chekhovich, V.Y. (1997) Flow of Cryogenic Fluid Film on a Vertical Surface. Thermal Physics Aeromechanics, 4, 307-317.
- 11. Alekseenko, S.V., Nakoryakov, V.Е. and Pokusaev, B.G. (1992) Wave Flow of Fluid Films. Publishing House “Nauka”, Novosibirsk, 256 p.
- 12. Chen, J.Z., Darhuber, A.A., Troian, S.M. and Wagner, S. (2004) Capacitive Sensing of Droplets for Microfluidic Devices Based on Thermocapillary Actuation. Lab on a Chip, 4, 473-480.
https://doi.org/10.1039/b315815b - 13. Seryakov A.V. (2015) Capacitance Sensor for Determination of a Fluid Layer Thickness. Utility Model Patent No. 152108, Bulletin No. 18/2015.
- 14. Seryakov, A.V., Konkin, А.V. and Belousov, V.K. (2012) Application of a Jet Steam Nozzle in Medium-Temperature Range Heat Pipes. Bulletin of Siberian State Aerospace University, 1, 142-147.
- 15. Seryakov, A.V. (2013) Velocity Measurements in the Vapour Channel of Low-Temperature Range Heat Pipes. International Journal of Engineering Research & Technology, 2, 1595 -1603.
- 16. Akhadov, Y.Y. (1972) Dielectric Properties of Pure Fluids. National Standard Reference Data Service Guide. Standards, Moscow, 412 p.
- 17. (1976) Tables of Physical Values. Guide under the Editorship of Kikoin I.K., the Member of Academy of Science. Atomizdat, Moscow, 1008 p.
- 18. Fuoss, R.M. (1968) Pressure Dependence of Dielectric Constant and Density of Liquids. Journal of Physical Chemistry, 72, 1057-1064.
https://doi.org/10.1021/j100849a048 - 19. Freeeman, G.R. (1986) Dielectric Constant against Temperature for 43 Liquids. Journal of Chemical Thermodynamics, 18, 221-234.
https://doi.org/10.1016/0021-9614(86)90050-9 - 20. Schaaf, A. (1974) Mitteilung beitrage zur problrmatik des einsatzes von kunststoffbehaltern fur flussige arzneizubereitungen. Pharmazie, 29, 708-711.
- 21. Nespital, W. (1932) Beschreibung einer kristallgesteuerten resonanzapparatur. Zeitschrift fur Physikalische Chemie, 16, 221-233.
- 22. Moll, W.L.H. (1939) Dielectrical Study of the Effect of Organic Solvent on High-Molecular Substances. Kolloidchemische Beihefte, 49, 1-74.
- 23. Kyropoulos, S. (1926) Die druckabhangigkeit der dielektrizitatskonstante einiger flussigkeiten bis zu 3000kg/cm2. Zeitschrift fur Physik, 40, 507-520.
https://doi.org/10.1007/BF01440828 - 24. Winkler, C.A. (1951) Solvent Effect on Iodide Exchange. Canadian Journal of Chemistry, 29, 790-803.
https://doi.org/10.1139/v51-091 - 25. Patil, P.B. (2000) Dielectric Measurements on Methyl Acetate + Alcohol Mixtures Using the Time Domain Technique. Journal of Chemical Engineering Data, 45, 917-919.
https://doi.org/10.1021/je000066+ - 26. Patil, P.B. (2001) Temperature Dependent Dielectric Relaxation Study of Ethyl Acetate-Alcohol Mixtures Using the Time Domain Technique. Journal of Molecular Liquids, 94, 27-36.
https://doi.org/10.1016/S0167-7322(01)00239-2 - 27. Mehrotra, S.C. (2001) Static Dielectric Constant and Relaxation Time for the Binary Mixture of Water, Ethanol, N,N-Dimethylformamide, N,N-Dimethylsulphoxide, and N,N-Dimethylacetamide with 2-Methoxyethanol. Bulletin of the Korean Chemical Society, 22, 357-361
- 28. Fernandes, D.P., et al. (1997) A Formulation for the Static Permittivity of Water and Steam at Temperatures from 238 K to 873 K at Pressures up to 120 MPa, Including Derivatives and Debye-Huckel Coefficients. Journal of Physical and Chemistry Reference Data, 26, 1125-1166.
https://doi.org/10.1063/1.555997 - 29. Fernandes, D.P., et al. (1995) A database for the Static Dielectric Constant of Water and Steam. Journal of Physical and Chemistry Reference Data, 24, 33-69.
https://doi.org/10.1063/1.555977 - 30. Seryakov, A.V. (2016) Characteristics of Low Temperature Short Heat Pipes with a Nozzle-Shaped Vapour Channel. Journal of Applied Mechanics and Technical Physics, 57, 69-81.
https://doi.org/10.1134/S0021894416010089 - 31. Seryakov, А.V. (2013) Changing the Temperature by Using Thermistors. Bulletin of Siberian State Aerospace University, 1, 167-172.
- 32. Seryakov, А.V. (2013) Enhancement of Precision of Temperature Measurements Using Thermistors. Sensors and Systems, No. 1, 38-42.
- 33. Seryakov, A.V. (2013) A New Method for Temperature Measurement Using Thermistors. International Journal of Engineering Research & Technology, 2, 444-454.
- 34. Seryakov, A.V. (2013) A Universal Method for Temperature Measurement Using Thermistors. Engineering and Technology Research, 1, 014-020.
- 35. Faghri, A. (1995) Heat Pipe Science and Technology. Taylor and Francis, Washington.
- 36. Vargaftic, N.B. (1963) Spravochnick po teplophizicheskim svoistvam gasov i zhidkostey. Publishing House of Physico-Mathematical Literature, Moscow, 708 p.
- 37. Lee, R., Reges, J. and Almenas, K. (1984) Size and Number Density Change of Droplet Populations above Front during Reflood. International Journal of Heat and Mass Transfer, 27, 573-585
- 38. Kreith, F. and Sonju, O. K. (1965) The Decay of a Turbulent Swirl Flow in a Pipe. Journal of Fluid Mechanics, 22, 257-271.
https://doi.org/10.1017/S0022112065000733 - 39. Huang, F. and Tsou, F.K. (1979) Friction and Heat Transfer in Turbulence Free Swirl Flow in Pipes. Transactions—ASME: Journal of Heat Transfer, 39, 1-9.
- 40. Adrian, B. and Allan, K.D. (2003) Heat Transfer Enhancement. In: Heat Transfer Handbook, Chap. 14, Wiley-Interscience. NY, 1033-1101, 1496 p.
- 41. Royal, J.H. (1975) Augmentation of Horizontal in Tube Condensation of Steam. Retrospective Theses and Dissertation, IOWA State University, Paper 5634.
- 42. Shih, T.H., Liou, W.W., Shabbier, A., Yang, Z. and Zhu, J. (1995) A New k-ε Eddy-Viscosity Model for High Reynolds Number Turbulent Flow-Model Development and Validation. Computers and Fluids, 24, 227-238.
https://doi.org/10.1016/0045-7930(94)00032-T
Appendix
The polynomial equation that describes the capacity value of the “drowned” sensor depending on thickness h, mm, and of the water layer above its gauging surface within the thickness range fluctuation of the layer h: 0 ? 4 mm is as follows:

The polynomial equation that describes the capacity value of the “dry” sensor depending on distance h, mm, between the sensor’s gauging surface and the calibration fluid’s surface approaching it can be presented as follows:

Dimension С(h) is presented in pF, h in mm and the standard deviation is σ = 0.002732, R2 = 0.9875829.
The polynomial equation describing the capacity value of the drowned sensor depending on thickness h, mm, of the water layer over its measuring surface within the thickness range variation of the layer h: 0 - 500 μm is as follows:

Dimension С(h) is presented in pF, h in μm, standard deviation σ = 0.0015552, R2 = 0.9968854
The polynomial equation describing the frequency difference of the measuring and reference generators, in relation to the water layer thickness of the measuring surface of the capacitance sensor, can be presented in the following manner:

Dimension Δf is stated in kHz, h in mm, standard deviation σ = 0.5177921, R2 = 0.9995247.
The polynomial approximation of the open capacitance sensor sensitivity for small thicknesses of measured fluid film (water) is as follows:

Dimension 
The polynomial equation that describes the change of the frequencies difference in the gauging generator and reference generator depending on the ethyl alcohol layer thickness on the gauging surface of the capacitance sensor may be presented as follows:

Dimension Δf is stated in kHz, h in mm, standard deviation σ = 0.504563, R2 = 0.999852.
The polynomial equation that describes the change of the frequencies difference in the gauging generator and reference generator depending on the diethyl ether layer thickness on the gauging surface of the capacitance sensor may be presented as follows:

Dimension Δf is stated in kHz, h in mm, standard deviation σ = 0.670613, R2 = 0.9988017.
Nomenclature
a and b: numerical coefficients;
A: nondimensional constant about a unit;
B: coefficient with account for thermophysical properties of the working fluid and structural parameters of the evaporator (porosity, typical dimension of channels and pores);
E: thermal power, supplied in the evaporator of the HP, W;
EB: thermal power, wherein the process of bubble boiling begins in the grid evaporator W;
F(z): surface area of the evaporator inside the vapour channel of the HP, m2;
f: decreased frequency of an output signal of the gauging generator with a fluid film that has formed on the gauging surface of the capacitance sensor, MHz;
f0: frequency of an output signal of the reference generator equal to 33 MHz;
Δf: difference between frequencies of a reference generator and a gauging generator, Hz;
fpuls: pulsations frequency on the surface of the liquid condensate film, Hz;
Gdr: mass flow of microdrops of the saturated vapour over the evaporator, kg/s;
Gmix: mass flow of moist saturated vapour over the evaporator, kg/s;
GVP: mass flow of dry saturated vapour over the evaporator, kg/s;
kB: Boltzmann’s constant, kB = 1.38065 × 10−23 J/K;
КHP: heat transfer coefficient through the cross section of the vapour channel of the heat pipe, W/K;
L: the length of the vapour channel of the HP, m;
Мdr: total mass of microdrops per unit volume of the droplet vapour flow over the evaporator, kg;

mvp: mass of molecule of diethyl ether, kg;
Мvp: vapour mass per unit volume of the droplet vapour flow over the evaporator, kg;
ndr: total number of microdrops of all sizes per unit volume of the droplet vapour flow over the evaporator, 1/m3;
ndri: number of microdrops of the working fluid with radius rdri per unit volume of the droplet vapour medium, 1/m3;
nvp(Tev): average number of dry vapour molecules in the unit volume of the vapour channel over the evaporator, m−3;

NA: Avogadro constant, mol−1;
P: vapour pressure near the condensation surface of the heat pipe, Pa;
P*: vapour pressure over the surface of the evaporator, which stops the process of boiling in the capillary-porous evaporator, Pa;
P(Tcond): vapour pressure near the condensation surface of the heat pipe, Pa; P(Tev): vapour pressure near the surface of the evaporator of the heat pipe, Pa;
ΔPvp: vapour pressure difference over the evaporator and near the condensation surface in the vapour channel of HP, Pa;
dP/dT: pressure derivative with respect to temperature of diethyl ether within the HP, Pa/K;
q: heat flow density, W/m2;
ΔQ: heat energy, absorbed in the evaporator over a period of
h: thickness of the gauged fluid film (layer), m;
ra: arithmetic middling radius of microdrops in two-phase droplet vapour flow, m;
rdri: radius of the i microdrop in the unit volume of the droplet vapour flow over the evaporator, m;
r(TB): specific vapourization heat of the working fluid in the HP, in the general case, depend upon temperature and pressure, J/kg;
r(Tcond): specific vapourization heat of the working fluid in the HP near the condensation surface, J/kg;
RC: electric resistance of the thermistor, Ohm, at temperature T, K;
Rfilm: heat resistance of the condensate film, K/W;
Rev(T): heat resistance of the flat evaporator, including outer wall of the HP, K/W/m2;
TB(P): boiling temperature of the working fluid, К;
T: temperature, K;
Tcond: temperature of the condensation surface, К;
Tev: temperature of the surface of the evaporator, К;
udr: average velocity of the microdrops movement in the vapour flow, m/s;
uvp: average velocity of the vapour phase, m/s;
Vφ: tangential component of the condensate film flow velocity, m/s;
Vr: radial components of the condensate film flow velocity, m/s;
z: longitudinal coordinate along the centroidal axis of the heat pipe, m;
Greek Symbols
α: the heat transfer coefficient of the evaporator, W/m2K;
γ: absolute moisture degree of the droplet vapour flow;
γG: degree of moisture discharge of the droplet vapour flow;
δ: average value of the film thickness on the condensation surface inside HP, m;
η: coefficient of dynamic viscosity of the dry vapour, Pa・s;
ηmix: coefficient of dynamic viscosity of the moist vapour with microdrops, Pa・s;
λ: coefficient of thermal conductivity of the working fluid condensate film, W/m・K;
Λ: penetration (spreading) depth of electric field above the gauging electrodes of the open capacitance sensor, m;
μvp: molar mass of diethyl ether vapour, kg/mol;
νL: specific volume of the working fluid on the liquid-vapour coexistence line, m3/kg;
νVP: specific volume of the saturated vapour, m3/kg;
ρL: density of microdrops of the working fluid, kg/m3;
ρvp: density of the dry vapour, kg/m3;
ρVP(Tcond): vapour density of diethyl ether near the condensation surface, kg/m3;
ρVP(Tev): vapour density of diethyl ether over the evaporator, kg/m3;


σ: dispersion or standard deviation of a smoothed curve regarding experimental values;
Δτ: unit time, s;
Δτ0: cycle pulse duration, s;
Δτ0num: numerical value of the cycle pulse duration, s;
Δτcond: cycle duration of pressure decrease due to condensation near the HP condensation surface, s;
Δτev: cycle duration of pressure increasing prior to the cessation of the boiling process in the evaporator, s;
ΔτHP: duration of pressure pulse propagation through the vapour channel of the heat pipe, s;


ψ: phase slip ratio of the droplet vapour flow, equal to the relation between average velocities of the microdrops movement and the vapour phase
ω: circular frequency of pulsations on the surface of liquid condensate film, Hz.
Subscripts
C: Thermistor
Film: Condensate film of the working fluid
φ: Tangential component velocity
r: Radial component velocity
wr: Radial shearing friction stress
wφ: Tangential shearing friction stress
Submit or recommend next manuscript to SCIRP and we will provide best service for you:
Accepting pre-submission inquiries through Email, Facebook, LinkedIn, Twitter, etc.
A wide selection of journals (inclusive of 9 subjects, more than 200 journals)
Providing 24-hour high-quality service
User-friendly online submission system
Fair and swift peer-review system
Efficient typesetting and proofreading procedure
Display of the result of downloads and visits, as well as the number of cited articles
Maximum dissemination of your research work
Submit your manuscript at: http://papersubmission.scirp.org/
Or contact eng@scirp.org