Engineering
Vol. 5 No. 1 (2013) , Article ID: 26533 , 6 pages DOI:10.4236/eng.2013.51007
An Improved Kernel K-Mean Cluster Method and Its Application in Fault Diagnosis of Roller Bearing
1Engineering Research Center of Advanced Mining Equipment, Ministry of Education, Hunan University of Science and Technology, Xiangtan, China
2Hunan Provincial Key Laboratory of Health Maintenance for Mechanical Equipment, Hunan University of Science and Technology, Xiangtan, China
Email: linlyjiang@163.com, alsace198@126.com, 312194703@qq.com
Received November 12, 2012; revised December 11, 2012; accepted December 20, 2012
Keywords: Improved Kernel K-Mean Cluster; Fault Diagnosis; Roller Bearing
ABSTRACT
For the kernel K-mean cluster method is run in an implicit feature space, the initial and iterative cluster centers cannot be defined explicitly. Against the deficiency of the initial cluster centers selected in the original space discretionarily in the existing methods, this paper proposes a new method for ensuring the clustering center that virtual clustering centers are defined in the feature space by the original classification as the initial cluster centers and the iteration clustering centers are ensured by the further virtual classification. The improved method is used for fault diagnosis of roller bearing that achieves a good cluster and diagnosis result, which demonstrates the effectiveness of the proposed method.
1. Introduction
The kernel K-mean cluster method is a combination of kernel method and K-mean method that the original items are embedded into a vector space called the feature space fist, and then K-mean cluster is performed in the feature space [1-2]. The initial cluster centers have an important influence on the cluster result. For example, the cluster result would be different by choosing different initial clusters, and there would obtain a local optimum rather than global optimal cluster result if choosing improper initial cluster center [3,4]. For the kernel K-mean cluster method is run in an implicit feature space, the initial and iterative cluster centers cannot be defined explicitly. To address this issue, L. Zhang [5] proposed the kernel clustering algorithm, in which the initial cluster centers are given freely in the original space and the iteration clustering centers are changed through transforming the kernel matrix to realize the algorithm iterative. This process is complicated and difficult to understand. R. Kong [6] adopted the kernel K-mean clustering, in which the initial cluster centers are arbitrarily given in the original space, and the iteration clustering centers are obtained according to the previous classification results, which choose every sample of every category as a clustering center respectively, to calculate the intra-class distance between the other sample points and the clustering center, the iteration cluster centers are the point with the minimum sum of distances. The paper combines the two perspectives and puts forward a new kernel K-mean clustering algorithm execution method, which uses virtual initial classification to determine the initial kernel clustering centers, and the iterative classification to determine the new virtual kernel clustering centers to ultimately achieve accurate clustering. The proposed method is applied in the diagnosis of rolling bearing clustering to verify the effectiveness of the method.
2. Kernel K-Mean Clustering Method
The K-mean clustering is an unsupervised learning algorithm proposed by J. MacQueen in 1967 and its core idea is divided the sample set of 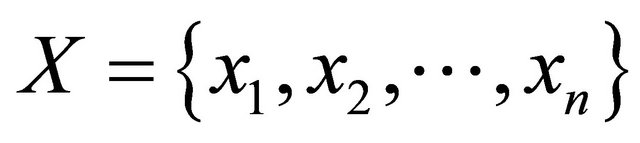 into K clustering, where the samples belong to the same calss have the higher similarity and samples belong to different class have lower similarity [7]. Detailed processing algorithm process is listed below:
into K clustering, where the samples belong to the same calss have the higher similarity and samples belong to different class have lower similarity [7]. Detailed processing algorithm process is listed below:
1) The initial clustering center is to select k sample of  discretionarily from n samples;
discretionarily from n samples;
2) Calculate the distance from each sample to the clustering center in turn and then assign the sample to the class of the minimum distance value, which represents the most similar with the clustering center. According to the approximation degree between the clustering center and the other sample, a certain sample x can be classified by the follow way:
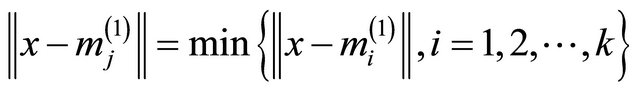 (1)
(1)
The sample![]() belongs to the clustering
belongs to the clustering 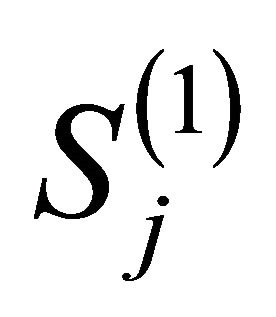 which corresponds with the center
which corresponds with the center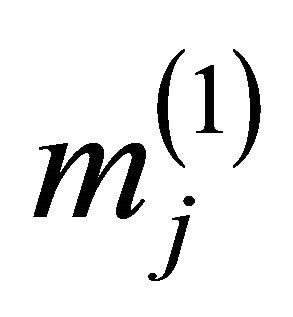 ;
;
3) After initial classification, calculate the k iteration clustering center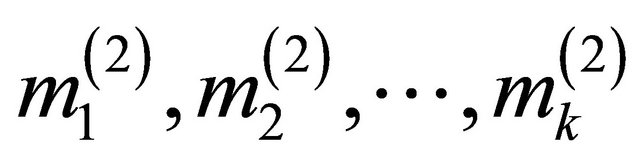 . It is different from the previous clustering center but will meet error sum of squares criterion:
. It is different from the previous clustering center but will meet error sum of squares criterion:
 (2)
(2)
make J minimum can get:
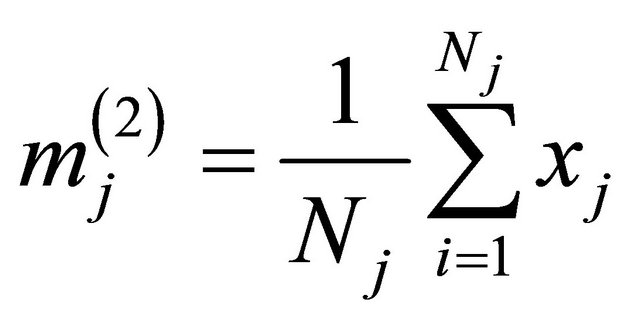 (3)
(3)
where 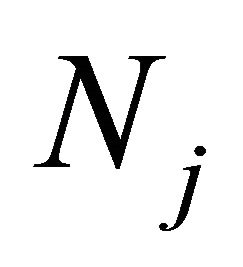 is the sample number of the class
is the sample number of the class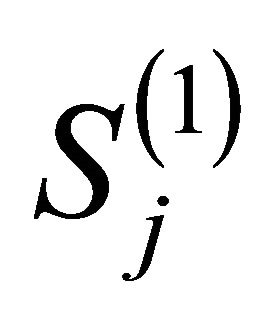 ;
;
4) Make a comparison with the previous iteration clustering center, if  switch to (2), otherwise switch to (5);
switch to (2), otherwise switch to (5);
5) Output clustering results.
Girolam first puts forward the ideas that make kernel method combine with clustering method. He believes that the nonlinear mapping is smooth and continuous. In the high dimensional space, sample in topology will remain the same struck with the original space, and when the categorical distribution was not suprasphere or ellipsoid, the clustering algorithm based on kernel is still valid.
Assume that nonlinear mapping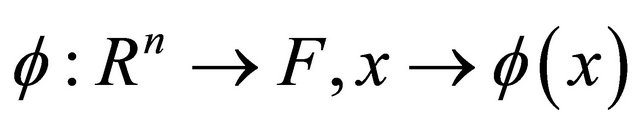 , mapping the sample
, mapping the sample![]() of original space
of original space 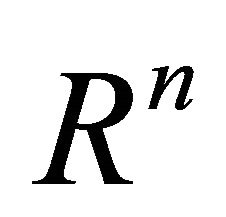 to the high dimensional feature space F, then in the feature space, the sample for classification will become:
to the high dimensional feature space F, then in the feature space, the sample for classification will become: 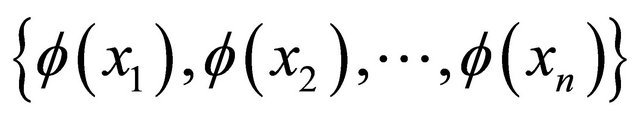 . The formula (2) which represents error sum of squares criterion function change into [8]:
. The formula (2) which represents error sum of squares criterion function change into [8]:
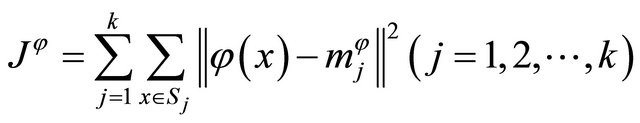 (4)
(4)
where the mean value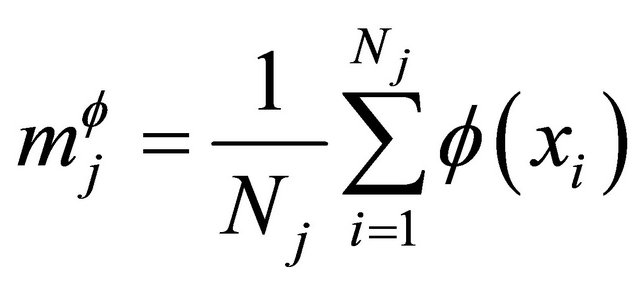 , and
, and 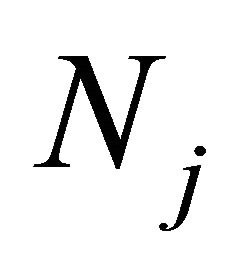 is the sample number of the jth class
is the sample number of the jth class , so:
, so:
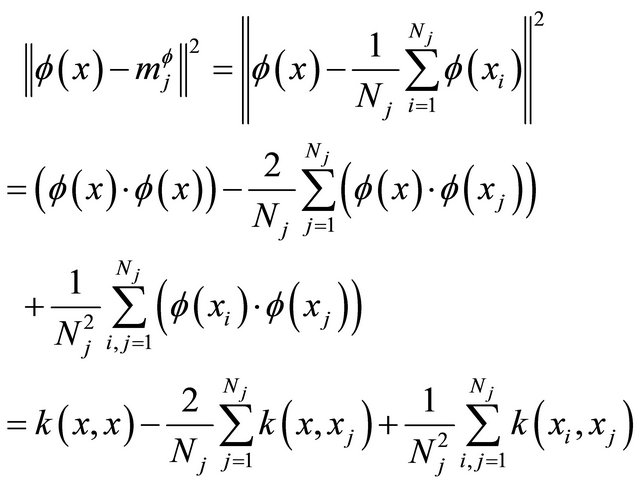 (5)
(5)
where k(x,x) was kernel function.
The distance between any two points and feature space:
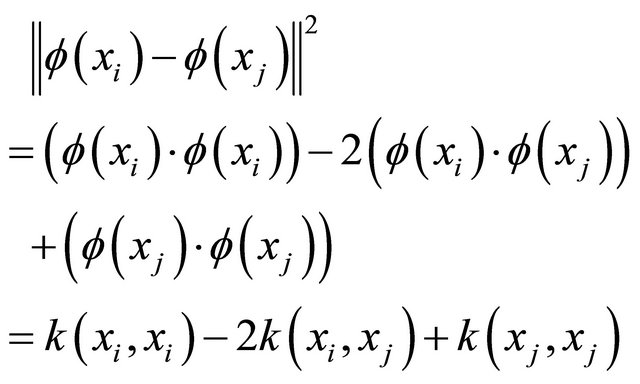 (6)
(6)
3. The Improved Kernel K-Mean Clustering Method
It can be found from formula (5) that, to calculate the distance between arbitrary point in feature space and kernel clustering center, it just need to know the original space coordinates of all samples which represented by kernel clustering center. The clustering center coordinates are always recessive in the original space or feature space which is just an intermediate variable. If determine the initial clustering center is equivalent to determine the initial classification and the next clustering center is equivalent to the new classification, so it can realize the kernel clustering according to the process as follows:
1) Determining the clustering categories k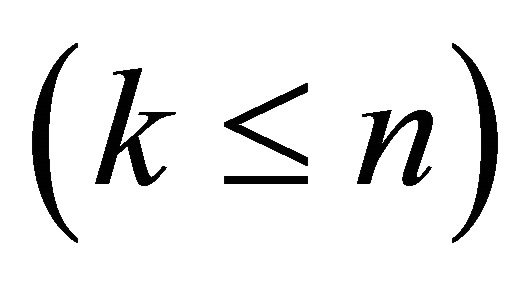 ;
;
2) Separating the sample set into k kind randomly;
3) Calculating the distance between each sample in feature space and clustering center according to the formula (5), then it can get a new sorting while assign the sample to the classes of the minimum distance;
4) Calculating the error sum of squares criterion function according to the formula (4), and judge whether criterion function is convergence or not, if it is not convergence, repeat the step 3), otherwise turn the step 5);
5) Outputting clustering results.
The process flow above is shown as in Figure 1.
4. Case Study
In order to verify the effectiveness of the improved kernel cluster method, the test of fault diagnosis of roller bearing is developed.
4.1. The Vibration Collecting Experiments
The vibration collecting experiments were performed on The Machinery Fault Simulator (MFS) from Spectra Quest, Inc. shown in Figure 2. It can simulate most of faults that commonly occur in rotating machinery, such as misalignment, unbalance, resonance, rolling bearing faults, gearbox faults, and so on. The simulator has a range of operating speeds up to 6000 rpm. In this work, the simulator is composed of a motor, a coupling, a testing rolling bearing fitted on the left of the shaft near the motor, a working rolling bearing on the other side, a bearing load and a shaft. The MFS provides a bearing
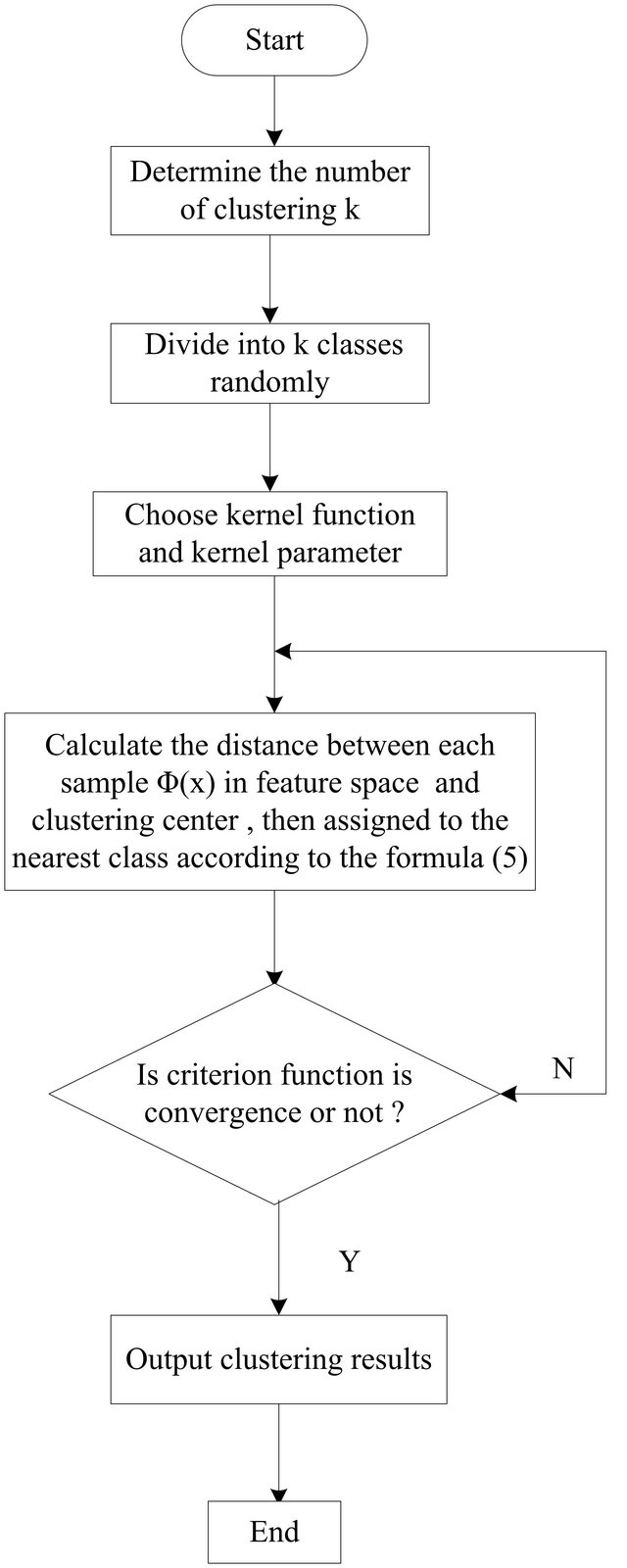
Figure 1. The process flow of the improved kernel K-mean cluster method.

Figure 2. Machinery fault simulator.
fault kit consisting of one inner race defect, one outer race defect, one with ball defect, and one combination of defects for performing experiments and studying bearing fault diagnosis.
The shaft rotating speed was obtained by a laser speedometer. Acceleration signals were measured using the Dewetron 16 channels data acquisition system and the IMI 603C01 accelerometers with 10 kHz acquisition frequency rate. The data were stored in .mat format for further Matlab operation.
4.2. Feature Extraction
Feature database 1: Time-domain statistical features of rolling bearing.
Vibration signals of rolling bearing with four fault models including normal, inner race defect, outer race defect and ball defect are taken for analysis. A total of 12 time-domain statistical features (shown in Table 1) are extracted from each vibration signal to constitute a fault sample. One hundred and ten fault samples from each model, total four hundred and forty samples are used to constitute the feature library 1.
Feature database 2: Energy features of rolling bearing in different frequency band based on 3-layer wavelet packet decomposition.
The 3-layer wavelet packet decomposition is performed on the vibration signals of roller bearing with four fault models. The different frequency branches are included in different layer of wavelet packet reconstructed signal, and when decomposing different fault mode of roller bearing, the reconstruction signals are different with each other. The result of decomposition is shown in Figure 3. The energy eigenvalue in each frequency
Table 1. The time-domain statistical features.

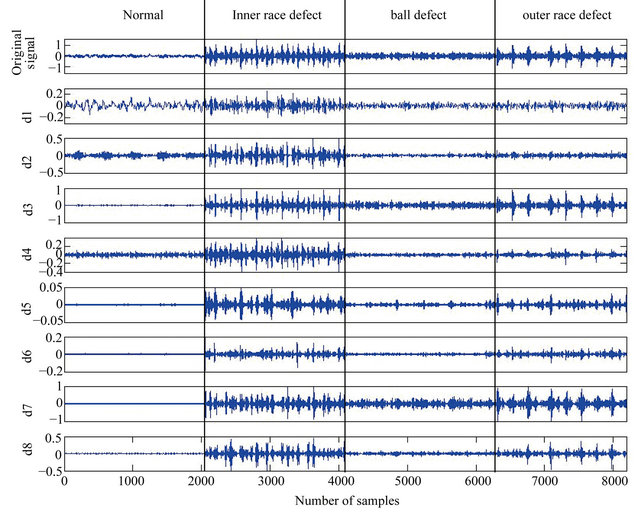
Figure 3. The 3-layer wavelet packet decomposition of roller bearing with deferent defects.
branch is calculated to constitute the fault sample. One hundred and ten fault samples from each model, total four hundred and forty samples are used to constitute the feature library 2.
Feature database 3: The first eight intrinsic mode functions (IMFs) energy features of rolling bearing based on empirical mode decomposition (EMD).
The empirical mode decomposition is performed on the vibration signals of roller bearing with four fault models. The different frequency branch is included in different intrinsic mode functions. When decomposing different fault mode of roller bearing, the reconstruction signals are different with each other. The result of decomposition is shown in Figure 4. The energy eigenvalue in each frequency branch is calculated to constitute the fault sample. One hundred and ten fault samples from each model, total four hundred and forty samples are used to constitute the feature library 3.
4.3. State Recognition and Fault Diagnosis
The improved kernel K-mean cluster analysis is conducted to the feature database 1 (time-domain statistical features of rolling bearing), the feature database 2 (energy features of rolling bearing in different frequency band based on 3-layer wavelet packet decomposition) and the feature database 3 (The first eight IMFs energy features of rolling bearing based on EMD). Gaussian kernel function is chosen and the kernel parameter σ is 100. A total of 10 experiments are conducted and average number is got. The results are shown in Table 2. It can be seen from the table that the improved kernel Kmean clustering algorithm is better than kernel K-mean clustering algorithm both in iterations and accuracy rate.
5. Conclusion
This paper studies on the kernel clustering methods. Aiming at the present deficiency of kernel K-mean clustering methods, this paper presents an executing process at kernel clustering method. The key of studying lies in the initial kernel cluster center and the iteration kernel clustering center. The case of roller bearing fault diagnosis indicated that the improved kernel K-mean clustering algorithm is better than kernel K-mean clustering algorithm both in iterations and accuracy rate. This study has significant instruction and reference value for the domain of fault diagnosis.
6. Acknowledgements
This work is supported by the national natural science
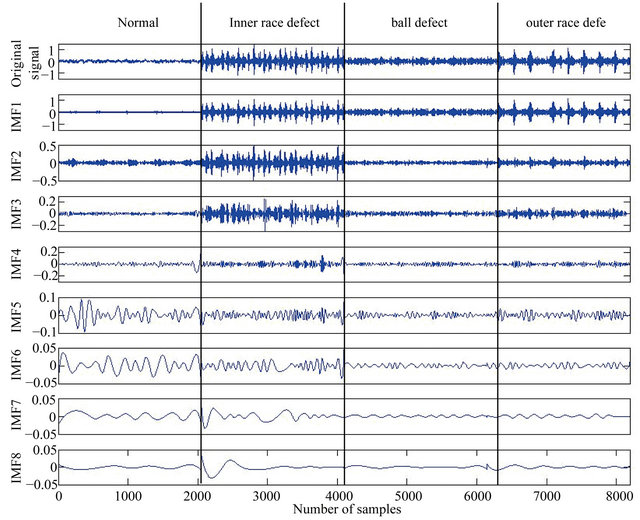
Figure 4. The empirical mode decomposition of roller bearing with deferent defects.
Table 2. A compare of different K-mean cluster methods.

foundation of China (51105138), the national high technology research and development program items (2012- AA041805), the Hunan province science and technology plan projects (2011GK3161), the scientific research fund of Hunan provincial education department (11C0530) and the aid program for science and technology innovative research team in higher educational institutions of Hunan province.
REFERENCES
- K. Yuchi, E. Yasunori and M. Sadaaki. “Indefinite Kernel Fuzzy c-Means Clustering Algorithms,” Lecture Notes in Computer Science, Vol. 6408, 2010, pp. 116-128. doi:10.1007/978-3-642-16292-3_13
- G. Daniel, P. Witold, “Kernel-Based Fuzzy Clustering and Fuzzy Clustering: A Comparative Experimental Study,” Fuzzy Sets and Systems, Vol. 161, No. 4, 2010, pp. 522-543. doi:10.1016/j.fss.2009.10.021
- C. Gu, S. Zhang, K. Liu and H. Huang, “Fuzzy Kernel K-Means Clustering Method Based on Immune Genetic Algorithm,” Journal of Computational Information Systems, Vol. 7, No. 1, 2011, pp. 221-231.
- G. Wang, X. Li and K. He, “Kernel Local Fuzzy Clustering Margin Fisher Discriminant Method Faced on Fault Diagnosis,” Journal of Software, Vol. 6, No. 10, 2011, pp. 1993-2000.
- L. Zhang, W. Zhou and L. Jiao, “Kernel Cluster Algorithm,” Chinese Journal of Computers, Vol. 25, No. 6, 2002, pp. 587-590.
- R. Kong, G. Zhang, Z. Shi and G. Li, “Kernel-Based K-Mean Clustering,” Computer Engineer, Vol. 30, No. 11, 2004, pp. 12-13,80.
- L. Kaufman and P. Rousseeuw, “Finding Groups in Data: An Introduction to Cluster Analysis,” Wiley Blackwell, Hoboken, 2005.
- Z. Wu, W. Xie and J. Yu, “Fuzzy c-Means Clustering Algorithm Based on Kernel Method,” Proceedings of International Conference on Computational Intelligence and Multimedia Applications, 27-30 September 2003, pp. 49-54.

