Engineering
Vol. 4 No. 7 (2012) , Article ID: 20536 , 4 pages DOI:10.4236/eng.2012.47050
Simulation Aspects of a Full-Car ATV Model Semi-Active Suspension
1Hindustan College of Engineering, Chennai, India
2Anna University, Chennai, India
3Ashok Leyland, Chennai, India
Email: kamalakannan.ka@gmail.com
Received April 20, 2012; revised May 7, 2012; accepted May 18, 2012
Keywords: ATV; BAJA SAEINDIA; SLA Wishbone; McPherson Strut; SAS (Semi Active Suspension) MATAB SIMULINK; Simulation and Testing
ABSTRACT
This paper is concerned with the design, modeling, and simulation and testing procedure of All Terrain Vehicle (ATV) fitted with SAS, which is used in BAJA SAEINDIA standards. Using CATIA V5, the model is created, which is fulfilling the guidelines of BAJA SAEINDIA rules. ATV is having the two different pairs of quarter car models of suspensions where dampers filled with MR Fluid (SAS) in front and rear wheels. In front SLA wishbone and rear McPherson Strut are fixed. The physical representation of the ATV is converted into the mathematical modeling and it is imported in MATLAB SIMULINK software and analyzed for ATV’s performance. The ATV is analyzed for its vertical, pitch and roll motions which include total number of 7 Degrees of Freedom. The road excitation modeling also incorporated with the equations. This paper, elaborates the approaching of simulation method only. The virtual model of ATV has involving greater significance of reducing the cost involved in real time testing as well as the results are replica of experimental results.
1. Introduction
Many papers are discussing the design, and various controllers used in quarter car/half car models provided with SAS. But the full car model with SAS is comparatively very less than above said models. A full car model has greater influence giving the closer to accurate results comparing with experimental to the simulation automotive [1] applications. The prime intention of using simulation is reducing the cost of experimental test as well as shortening the period of testing time. This paper’s prime intention is application of full car model of (Figure 1) ATV, designed conventional dampers in front wheels, and rear wheels are associated with SAS, and introducing simulation environment like MATLAB SIMULINK. The MATLAB environment is very much useful to simulate vehicle model in a convenient way.
Comfort and road handling performance of a passenger car is mainly controlled by the damping [2,3] characteristics of the shock absorber. Almost all types of spring and shock absorber for a car are designed assuming that, the surface of the road is a smoother one. But the surface is reverse against the assumption. So the negotiations between surface roughness and constant damper coefficients are not well balanced, causing increasing vibrations in the vehicles.
2. ATV’s Introduction
Mechanical design, as classically taught in engineering, has centered on the application of stress analysis theory. While this theory is important, actual industrial design is generally dependent upon manufacturability, time and cost constraints as well as stress analysis.
With this in mind, the SAE Mini Baja® competition [4] was originated at the University of South Carolina in 1976, under the supervision of Dr. John F. Stephens. Since then, the competition has grown to become a premier engineering design series. BAJA SAEINDIA, an annual competition for engineering students in India, was started 2007.
The ATV should run continuously for four hours in various terrains, especially loose and uneven roads with high bumps, deeper potholes and muddy terrain on the surface. The input from the road surface to the ATV is hard/soft and always varying its rattle space with body and suspension, longitudinal acceleration in forward motion and lateral acceleration when cornering. This property results reduced in steering stability, controlling and handling performance of the ATV by drivers [5]. The

Figure 1. ATV model.
other problem is higher risk of roll-over due to the translation of the centre of gravity (COG) of ATV at maneuvering in high speeds. It is very much important that the suspension characteristics ensure ATV’s stability on the track.
The conceptual idea of SAS is to replace active force actuators with continually adjustable elements, which can vary or shift the rate of the energy dissipation in response to instantaneous condition of motion. SAS can only change the viscous damping coefficient of the shock absorber; it will not add additional energy of the suspension system. The detailed explanation about the design steps of suspension system is given below.
3. Design of the Suspension System in ATV (Front and Rear)
3.1. Front and Rear Suspension
The double wishbone suspension can also be referred to as double “A” arms. It is called short long arm (SLA) suspension, if the upper and lower arms are of unequal length. For the front wheels of ATV SLA is provided for the following reasons. The upper arm is usually shorter to induce negative camber as the suspension jounces (rises). When the vehicle is in a turn, body roll results in positive camber gain on the inside wheel. The outside wheel also jounces and gains negative camber due to the shorter upper arm. This is the attempt to overcome these two effects to cancel out and keep the tire perpendicular to the ground. This is especially important for the outer tire because of the weight transfer to this tire during a turn. The Figures 2-3 shows SLA and Mc Pherson suspensions, respectively, of the ATV.
The other advantages of a SLA suspension are that it is as quick as possible to work out the effect of moving each joint .Adjusting of the kinematics of the suspension easily and optimize wheel motion. It is also easy to work out the loads that different areas in ATV, will be subjected to which allows more optimized lightweight parts
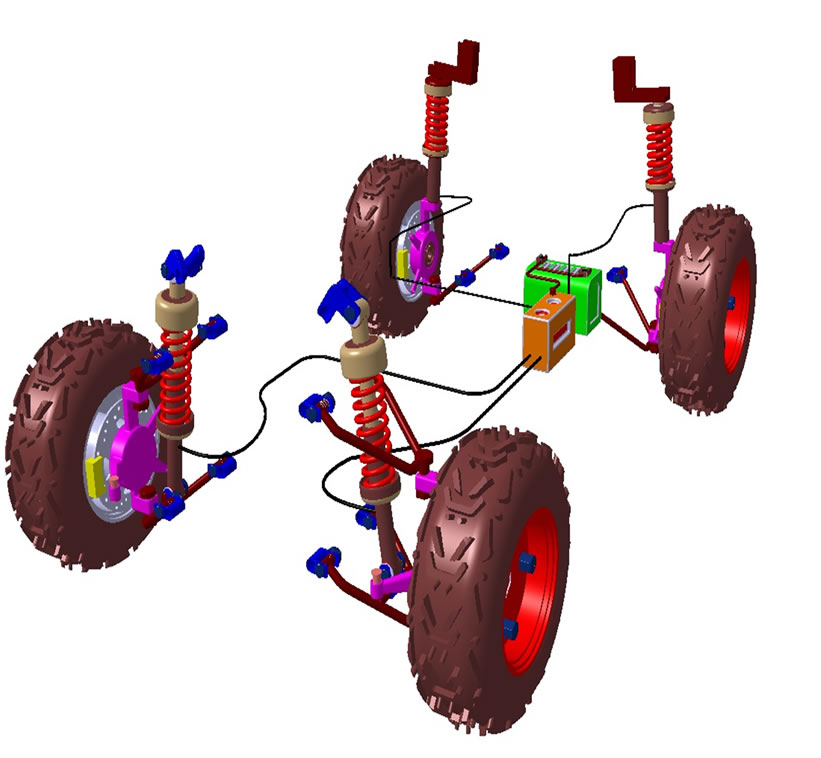
Figure 2. Front wheels and rear wheels with SLA suspensions and McPherson respectively.
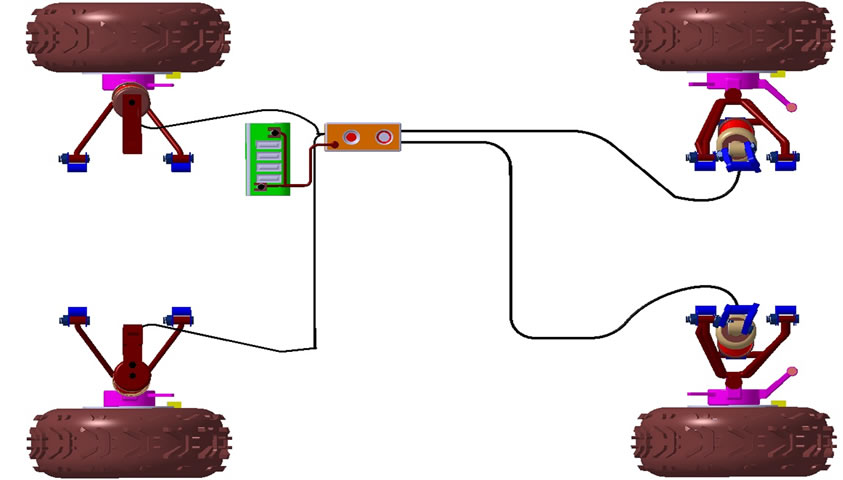
Figure 3. Top view of ATV.
to be designed.
The disadvantage is that it is slightly more complex than other systems like a McPherson strut. Due to the increased number of components within the suspension setup, it takes much longer to service and is heavier than an equivalent McPherson design. But for purpose of utilizing in ATV the servicing is not making much problem because, it is used in only one competition.
3.2. The McPherson Strut
The McPherson is a simple system that utilizes the piston rod of the built-in telescopic shock absorber to serve as the kingpin axis. Normally, a coil spring is mounted over the strut assembly, in which case, a thrust bearing at the top of the spring prevents spring wind-up during turns.
The lower link may be in the form of an ordinary A-arm. More commonly, a narrow transverse link locates the lower end of the strut in the transverse direction and a separate member called a radius rod locates the assembly in the longitudinal direction.
The advantages of the McPherson strut include its simple design of fewer components, widely spaced anchor points that reduce loads, and efficient packaging. But, its disadvantages include a relatively high overall height which tends encourage a higher hood and fender line, and its relatively limited camber change during jounce. A disadvantage on the consumer level is the comparatively high cost of servicing the shock absorber.
A small camber change during jounce and rebound is characteristic of the strut design. The vehicle roll center is controlled by raising or lowering the inboard anchor point of the transverse link, and by varying the steering axis inclination.
For the reverse the conventional type McPherson is replaced by SAS and suitable control algorithm as been provided.
4. Semi Active Suspension with MR Fluids
For the following benefits the MR fluids are used in dampers:
The Magnetoreological (MR) fluids can be quite promising for vibration reduction applications [6]. Dampers with controllable fluids are often known as rheological fluids. MR fluids are non colloidal suspensions of particles having size in order of a few microns (5 - 10 µm) [7]. The properties of these fluids are determined by polarizable particles within nonconductive carrier fluid. These particles being polarized the fluid become very viscous and difficult to move and responds faster, in mili seconds.
Semi-active systems can only change the viscous damping coefficient of the shock absorber, and do not add energy to the suspension system. Though limited in their intervention (for example, the control force can never have different direction than that of the current speed of the suspension), semi-active suspensions are less expensive to design and consume far less energy [8]. As shown in Figure 4, recent research in semi active suspensions narrows the gap between semi-active and fully active suspension systems. In active suspension, the power consumption is very large (at least 10% of engine power) but for SAS the power from the battery is enough. At the time of power failure, the active suspension is completely inactive. Because of the above reasons it has been considered and observed that SAS very much useful in ATV suspensions.

Figure 4. Vertical vibration of a car suspension.
5. Full Vehicle Model of ATV
In the first step of the modeling, the full vehicle model of the ATV is developed. This model includes the submodels of the tire, ATV body, wheels, and ATV suspension, etc.
5.1. Tire Model
Tires are the first elastic member between the road surface and ATV that have ideal characteristics in providing better isolation from the uneven profile of road disturbances, particularly the high frequency road input that is not damped effectively by a suspension system. On the other hand, the tires characteristics are related very fine to the quality of the tire-road contact and the vehicle handling.
5.2. Road Excitation Modeling
It has been already discussed [4] that, the ATV vehicle running terrain is an uneven surface (is neither a deterministic nor a random type inputs) with bumps, pot holes, hard and loose sands with muddy or without muddy. The road profile considered has above said discrete events as happening. So it is very important that for a vehicle dynamic simulation process, the road profile plays a vital role. Instead of using multi harmonic input or pseudorandom input, the better choice is Power Spectral Density (PSD). A stochastic model gives a more realistic representation of a road profile.
5.3. Quarter Car Suspension Model
The quarter-car model as shown in Figure 5 represents one of the four vehicle suspension units. It is a simplified model [1,8] with lumped masses and liberalized elements. This may appear to be an oversimplification model for a vehicle suspension system. However, the origins of the many ideas come from the fundamental work using this model. Particularly, this model is used in the area of modern control strategies for active and semi-active suspensions.
In this study, the quarter-car model is also used as basis for deriving of the full vehicle model. The fundamental parameters of a suspension system can be defined by this model. The motions of the sprung and unsprung masses can be determined by solving the system of differential equations. In the below sections, the quarter-car model will be explained as the basis of the full ATV model.
5.4. Full-Vehicle Model Degrees of Freedom
The quarter-car model can be used in order to evaluate the main characteristics of vehicle suspensions. However, a model with the two degrees of freedom of the sprung and unsprung masses covers just the vertical motions of a
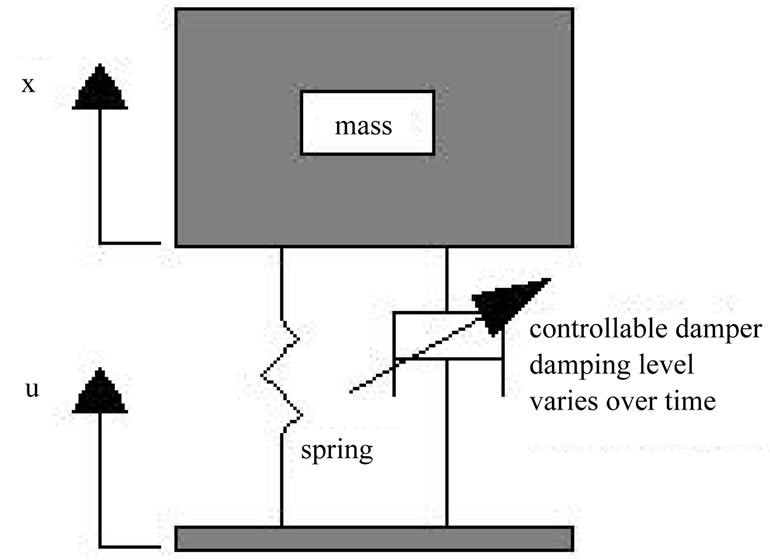
Figure 5. Quarter car semi-active suspension model.
vehicle, and in order to study the rotational motions, other models with more degrees of freedom are necessary. A full-vehicle model is able to cover all needed degrees of freedom. As before, it is necessary to define a proper coordinate system for dynamics of an ATV.
For this purpose, there are two [9] kinds of coordinate systems: space-fixed and vehicle-fixed system. In spacefixed system a point in space determines the position and orientation of a vehicle. This system is used in order to define the maneuver path of a vehicle. In opposition, vehicle-fixed coordinate system is originated at the center of gravity (CG) of a vehicle and travels with it. In the study of suspensions, the vehicle-fixed system is used in order to define a relative coordinate system for the dynamics of the suspension components.
According to the SAE convention, the positive directions of the axes are defined as follows:
1) X-axis: straight to the forward from the vehicle;
2) Y-axis: straight to the left from the vehicle;
3) Z-axis: straight to the upwards from the vehicle.
The above said DOF’s is converted into a physical representation. These represents are converted into the mathematical modeling for the simulation process in full vehicle rectangular form of lumped-mass dimensions determining the position of the modes. Now with respect to the vehicle fixed coordinate (Figure 6) system, the vehicle motions can be described. There are six degrees of freedom (6 DOF) related to the vehicle body motions including three translational and three rotational degrees of freedom. In addition, there are four dimensional degrees of freedom related to the unsprung masses, which is the number of the vehicle wheels. This vehicle motions and relevant terminology about vehicle body are described in this part.
In a body there are six degrees of freedom, (Table 1) which every axis containing of 2 DOF. The above said DOF’s is converted into a physical representation. These represents are converted into the mathematical modeling for the simulation process in full vehicle rectangular
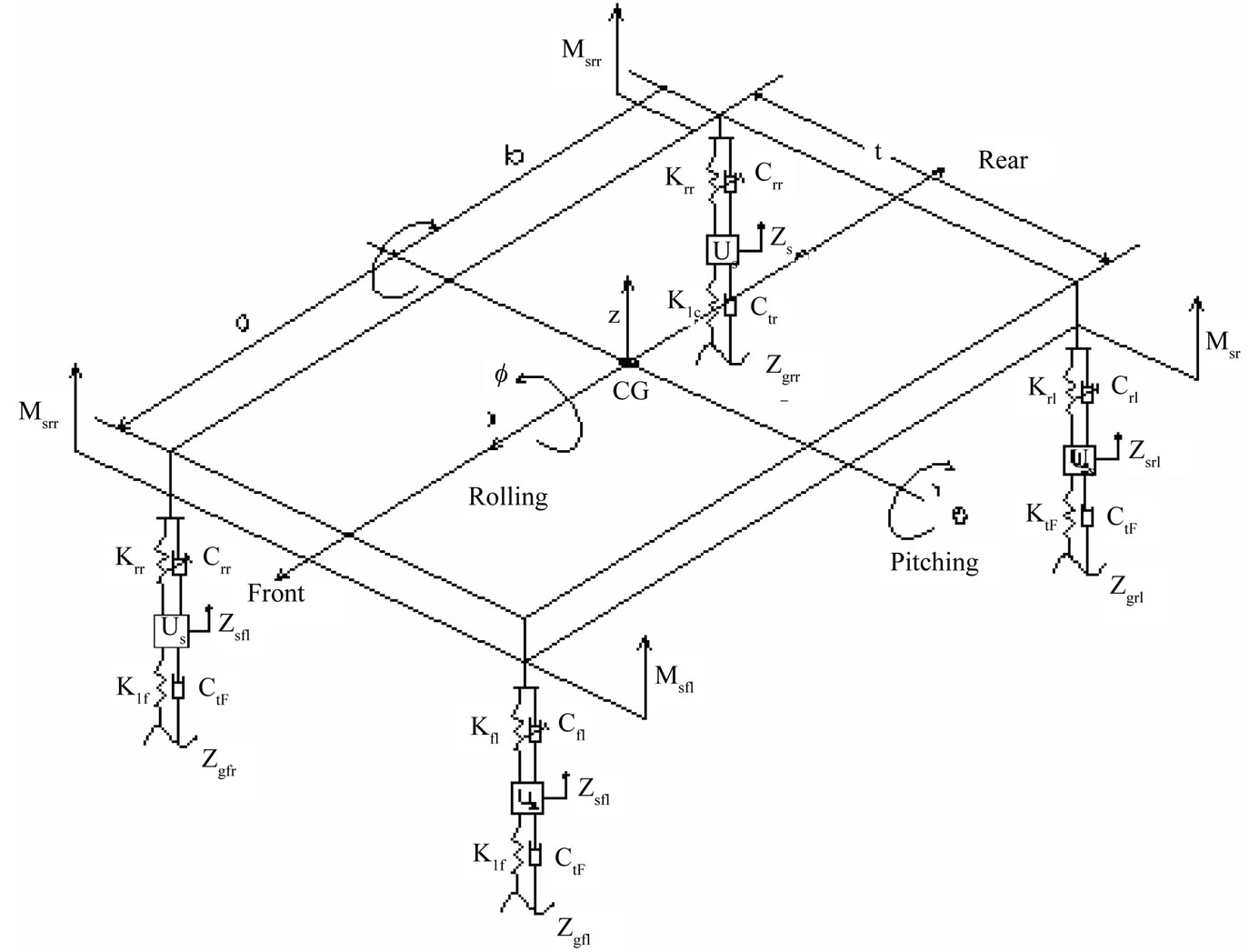
Figure 6. Full-ATV vehicle physical model with seven degrees of freedom.

Table 1. Considered degrees of the freedom in the full-vehicle model.
form of lumped-mass dimensions determining the position of models. This mass form has specific dimensions determining the position of the COG and position of the four suspension units standing on the corners of the body. In this modeling, it is also supposed that the axes of the roll and pitch cross the center of gravity .This model (Table 2) present a proper simplification. However, it is needed that the related mass and inertia parameters to be calculated accurately. In the reality, ATV body involves different masses standing on different position.
In order to precise the value of model parameters, the body of the ATV is considered a multi-rigid body mass. This mass includes that of engine, roll cage, Gear box, drive train etc., and it has been observed that the approximate weight distribution ratio from front and rear is 40:60, because all the above said components are provided rear side only.
6. Conclusions
This paper discusses the fundamentals of a full-car dynamic model of ATV. Primary important of the paper has been to show a direction, of an easy way to implement ATV’s behavior to the simulation software, in particular for SAS.
As discussed earlier, the SAS has been considered as the best solution to the ATV for its road handling behavior of that particular terrain, for the various events of dynamic tests includes hill climbing test, speed test, acceleration test, maneuverability test and endurance test. The expected results of vertical displacements, and both
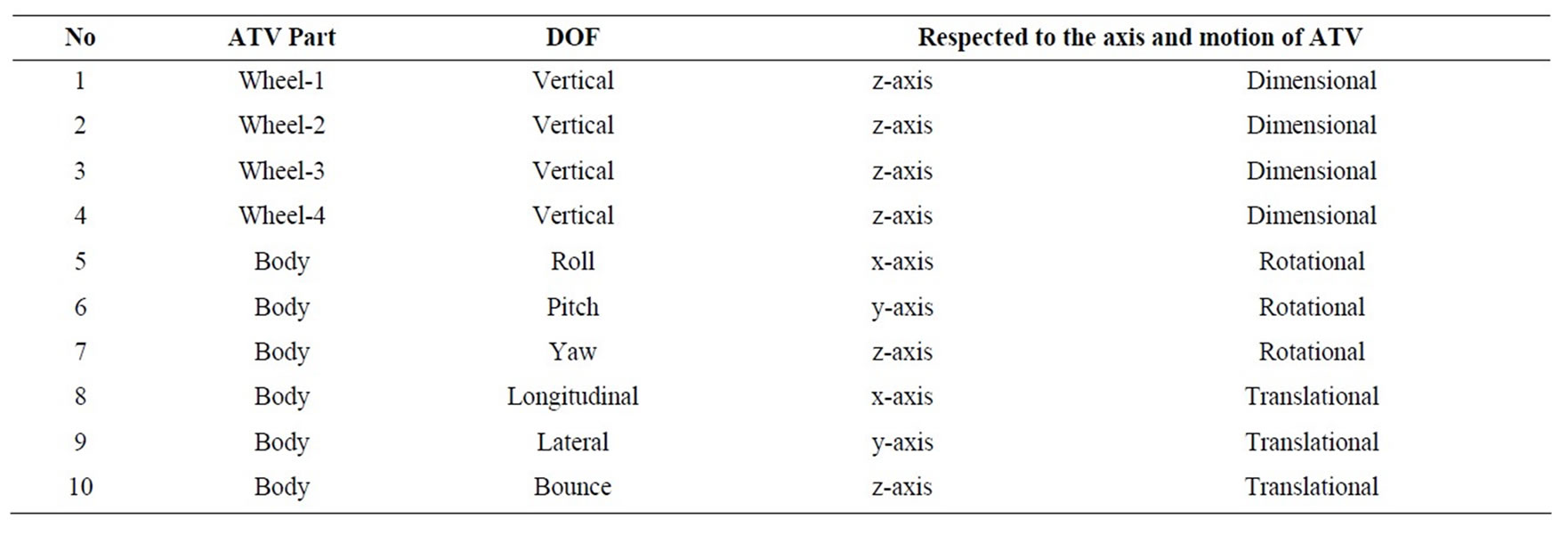
Table 2. DOF (10) in the full-vehicle model.
longitudinal and lateral accelerations to be controlled and it will be in the expected level.
The mathematical equations of the physical full-vehicle ATV model with seven degrees of freedom will be created with addition of longitudinal, vertical and lateral DOF. Road excitation inputs would be added into the equations. These equations shall be imported to a software implementation (MATAB SIMULINK) and simulation shall be done. The paper has been presented and some points are introduced to design the increase the comfortness of the ATV’s driver, and gives better handling performance of the vehicle.
REFERENCES
- W. Gao, N. Zhang and H. P. Du, “A Half Car Model for Dynamic Analysis of Vehicle with Random Parameters,” 5th Australasian Congress on Applied Mechanics, ACAM 2007, Brisbane, 10-12 December 2007.
- J. Wang, D. A. Wilson, W. David and A. Corolla, “Active Suspension to Improve Vehicle Ride and Steady State Handling,” 44th IEEE Conference on Decision and Control, 2005 and 2005 European Control Conference (CDC-ECC’05), 12-15 December 2005, pp. 1982-1987.
- M.-C. O. S. Popesc and N. E. Mastorakis, “Testing and Simulation of a Motor Vehicle Suspension,” International Journal of Systems Applications, Engineering & Development (IJSAED), Vol. 3, No. 2, 2009.
- www.bajasaeindia.org
- D. C. Karnopp, M. J. Crosby and R. A. Harwood, “Vibration Control Using Semi-Active Force Generators,” ASME Journal of Engineering for Industry, Vol. 96, No. 2, 1975, pp. 619-626. doi:10.1115/1.3438373
- R. M. Chalasani, “Ride Performance Potential of Active Suspension Systems-Part I Simplified Analysis Based on a Quarter-Car Model,” Proceedings of 1986 ASME Winter Meeting, Los Angeles, December 1986.
- W. H. Liao and C. Y. Lai, “Harmonic Analysis of a Magnetoreological Damper Publishing for Vibration Control,” Smart Materials and Structures, Vol. 11, No. 2, 2002, pp. 288-296.
- Emmanuelle Guglielmino, Tudor Sireteanu, Semi-Active Suspension Control-1153-1164, 2005.
- K. Kamalakkannan, A. ElayaPerumal, S. P. Mangalaramanan and K. Arunachalam, “Performance Analysis and Behaviour Characteristics of CVD (Semi-Active) in Quarter Car Model,” Jordan Journal of Mechanical and Industrial Engineering, Vol. 5, No. 3, 2010, pp. 261-265.

