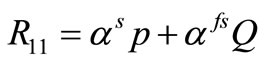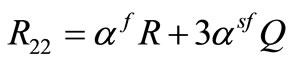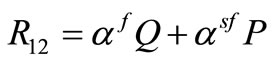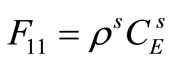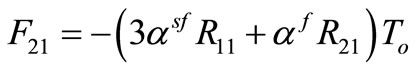Engineering
Vol. 3 No. 11 (2011) , Article ID: 8662 , 13 pages DOI:10.4236/eng.2011.311138
Generalized Porothermoelasticity of Asphaltic Material
Civil Engineering Department, Makkah, Kingdom of Saudi Arabia
E-mail: mhalawi@uqu.edu.sa
Received September 18, 2011; revised October 11, 2011; accepted October 20, 2011
Keywords: Porothermoelasticity, Asphaltic material, Thermal shock, Tod
ABSTRACT
In this work, a mathematical model of generalized porothermoelasticity with one rela-xation time for poroelastic half-space saturated with fluid will be constructed in the conte-xt of Youssef model (2007). We will obtain the general solution in the Laplace transform domain and apply it in a certain asphalt material which is thermally shocked on its bounding plane. The inversion of the Laplace transform will be obtained numerically and the numerical values of the temperature, stresses, strains and displacements will be illustrated graphically for the solid and the liquid.
1. Introduction
Due to many applications in the fields of geophysics, plasma physics and related topics, an increasing attention is being devoted to the interaction between fluid such as water and thermo elastic solid, which is the domain of the theory of porothermoelasticity. The field of porothermoelasticity has a wide range of applications especially in studying the effect of using the waste materials on disintegration of asphalt concrete mixture.
Porous materials make their appearance in a wide variety of settings, natural and artificial and in diverse technological applications. As a consequence, a variety of problems arise while dealing with static and strength, fluid flow, heat conduction and the dynamics of such materials. In connection with the later, we note that problems of this kind are encountered in the prediction of behavior of sound-absorbing materials and in the area of exploration geophysics, the steadily growing literature bearing witness to the importance of the subject [1]. The problem of a fluid-saturated porous material has been studied for many years. A short list of papers pertinent to the present study includes Biot [2,3], Gassmann [4], Biot and Willis [5], Biot [6], Deresiewicz and Skalak [7], Mandl [8], Nur and Byerlee [9], Brown and Korringa [10], Rice and Cleary [11], Burridge and Keller [12], Zimmerman et al. [13,14], Berryman and Milton [15], Thompson and Willis [16], Pride et al. [17], Berryman and Wang [18], Tuncay and Corapcioglu [19], Alexander and Cheng [20], Charlez, P. A., and Heugas, O. [21], Abousleiman et al. [22], Ghassemi, A. [23] and Diek, A S. Tod [24].
The thermo-mechanical coupling in the poroelastic medium turns out to be of much greater complexity than that in the classical case of impermeable elastic solid. In addition to thermal and mechanical interaction within each phase, thermal and mechanical coupling occurs between the phases, thus, a mechanical or thermal change in one phase results in mechanical and thermal changes throughout the aggregate of asphaltic concrete mixtures. Following Biot, it takes one physical model to consist a homogeneous, isotropic, elastic matrix whose interstices are filled with a compressible ideal liquid both solid and liquid form continuous (and interacting) regions. While viscous stresses in the liquid are neglected, the liquid is assumed capable of exerting a velocity- dependent friction force on the skeleton. The mathematical model consists of two superposed continuous phases each separately filling the entire space occupied by the aggregate. Thus, there are two distinct elements at every point of space, each one characterized by its own displacement, stress, and temperature. During a thermomechanical process they may interact with a consequent exchange of momentum and energy.
Our development Proceeds by obtaining, the stressstrain-temperature relationships using the theory of the generalized thermo elasticity with one relaxation time “Lord-Shulman” [25]. Moreover, to the usual isobaric coefficients of thermal expansion of the single-phase materials, two coefficients appear which represent measures of each phase caused by temperature changes in the other phase.
As a result of the presence of these “coupling” coefficients, it follows that coefficient of thermal expansion of the dry material which differs than that of the saturated ones and the expansion of the liquid in the bulk is not the same as of the liquid phase. Putting into consideration the applications of geophysical interest, it takes the coefficient of proportionality in the dissipation term to be independent of frequency, that is, we confine ourselves to low-frequency motions. The last constituent of the theory is the equations of energy flux. Because the two phases in general, will be at different temperatures in each point of the material, there is a rise of a heat-source term in the energy equations representing the heat flux between the phases. It has been taken this “interphase heat transfer” to be proportional to the temperature difference between the phases. Finally, by using the uniqueness theorem the proof has been done.
Recently, Youssef has constructed a new version of theory of porothermoelasticity, using the modified Fourier law of heat conduction. The most important advantage for this theory, is predicting the finite speed of the wave propagation of the stress and the displacement as well as the heat [26].
In this work, a mathematical model of generalized porothermoelasticity with one relaxation time for poroelastic half-space saturated with fluid will be constructed in the context of Youssef model. We will obtain the general solution in the Laplace transform domain and apply it in a certain asphalt material which is thermally shocked on its bounding plane. The inversion of the Laplace transform will be obtained numerically and the numerical values of the temperature, displacement and stress will be illustrated graphically.
2. Basic Formulations
Starting by Youssef model of generalized porothermoelasticity [26], the linear governing equations of isotropic, generalized porothermoelasticity in absence of body forces and heat sources, are
1) Equations of motion
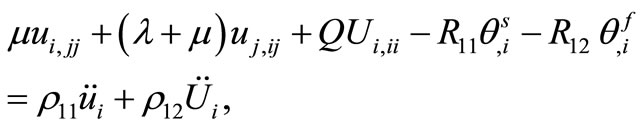 (1)
(1)
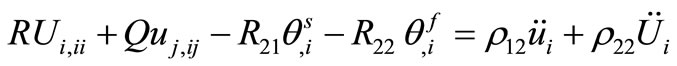 . (2)
. (2)
2) Heat equations
 (3)
(3)
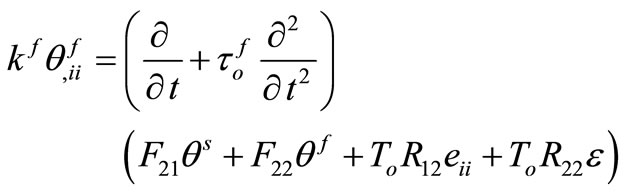 (4)
(4)
3) Constitutive equations
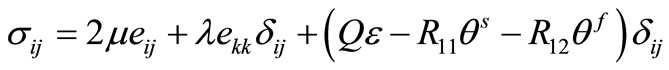 , (5)
, (5)
 . (6)
. (6)
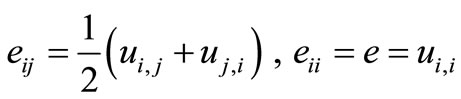 (7)
(7)
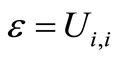 . (8)
. (8)
3. Formulation the Problem
We will consider one dimensional half-space 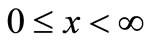 is filled with porous, isotropic and elastic material which is considered to be at rest initially. The displacement will be considered to be in one dimensional as follows:
is filled with porous, isotropic and elastic material which is considered to be at rest initially. The displacement will be considered to be in one dimensional as follows:
 , (9)
, (9)
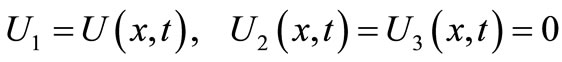 . (10)
. (10)
Then the governing equations (1)-(8) will take the forms:
1) Equations of motion
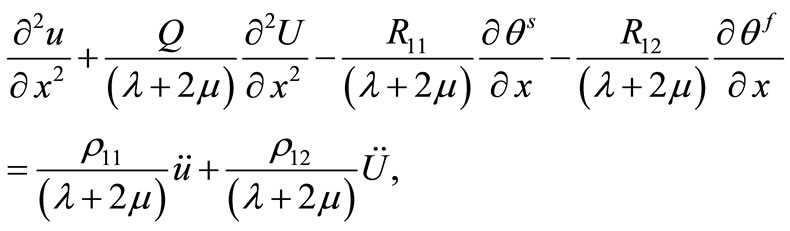 (11)
(11)
 . (12)
. (12)
2) Equation of heat
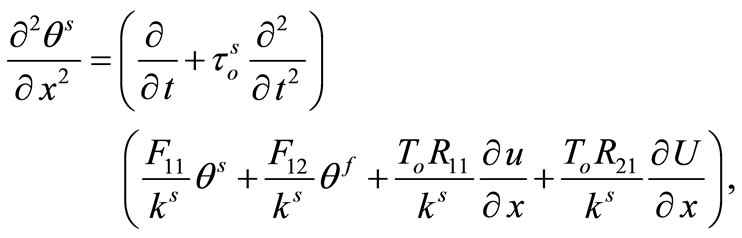 (13)
(13)
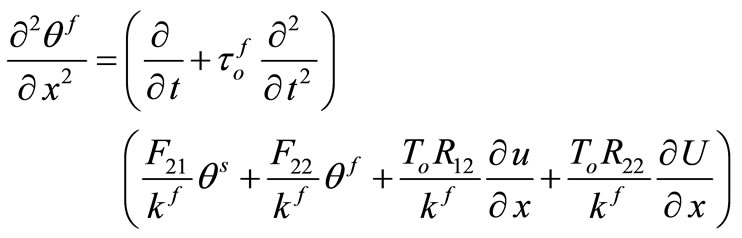 (14)
(14)
3) The constitutive relations
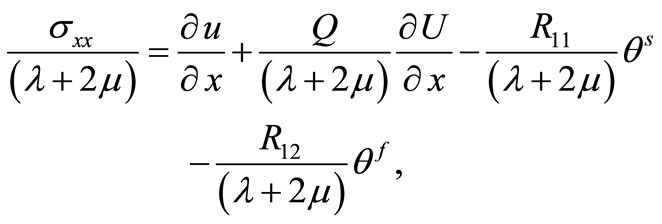 (15)
(15)
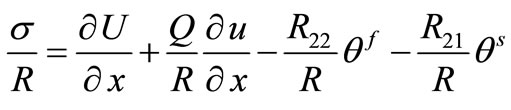 . (16)
. (16)
 (17)
(17)
 . (18)
. (18)
Using the non-dimensional variables as follows:
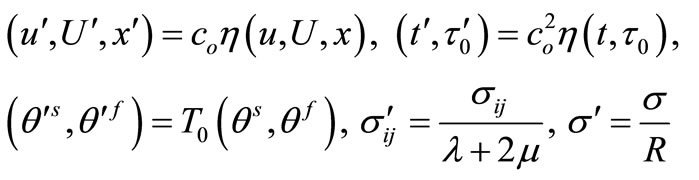
where
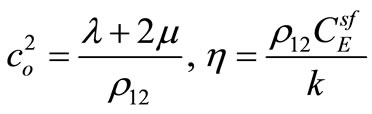 .
.
Then, we get
 (19)
(19)
 (20)
(20)
 (21)
(21)
 (22)
(22)
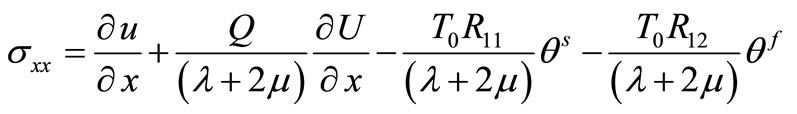 , (23)
, (23)
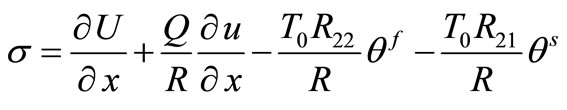 . (24)
. (24)
In the above equation, we dropped the prime for convenient.
4. Formulation the Problem in Laplace Transform Domain
Applying the Laplace transform for the both sides of the equations (19)-(24) which is defined as follows:

then, we get
 , (25)
, (25)
 , (26)
, (26)
 , (27)
, (27)
 , (28)
, (28)
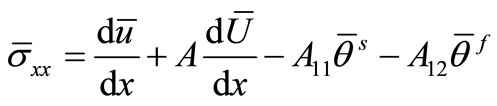 , (29)
, (29)
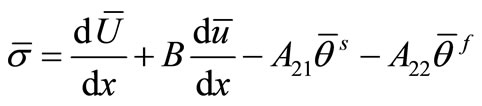 , (30)
, (30)
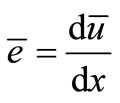 (31)
(31)
 . (32)
. (32)
where
 ,
,
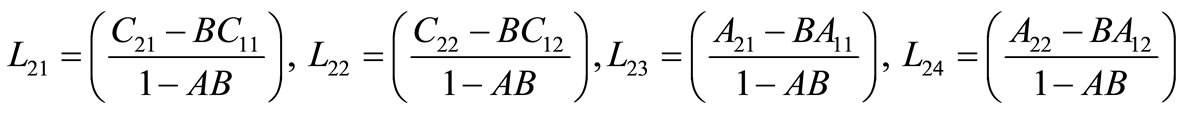 ,
,
 ,
,
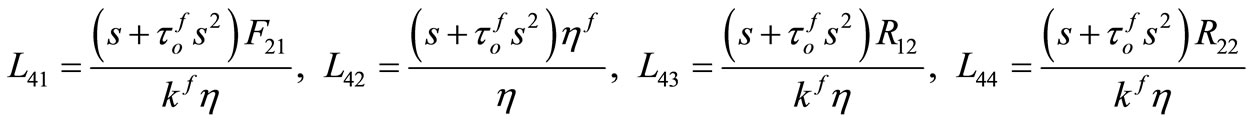 .
.
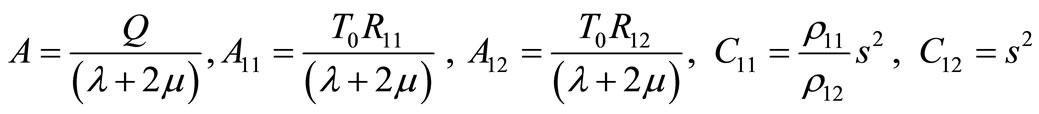

By using equations (25)-(28), we get
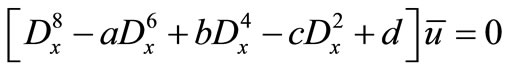 , (33)
, (33)
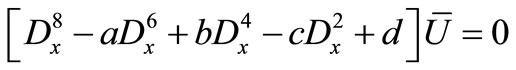 , (34)
, (34)
 , (35)
, (35)
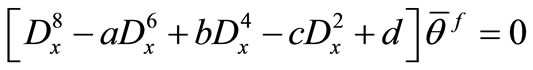 , (36)
, (36)
where
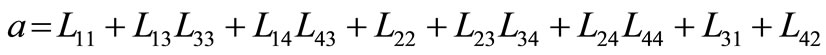


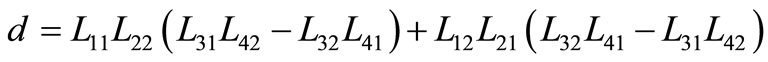 and
and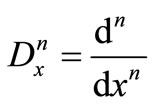 .
.
According to equations (33)-(36) and to bounded state of functions at infinity, we can consider the following forms
 , (37)
, (37)
 , (38)
, (38)
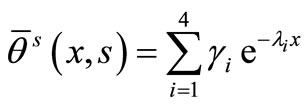 , (39)
, (39)
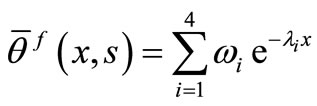 , (40)
, (40)
where 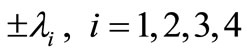 are the roots of the characteristic equation of the system (33)-(36) which takes the form
are the roots of the characteristic equation of the system (33)-(36) which takes the form
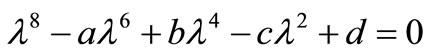 , (41)
, (41)
To get the relations between the parameters 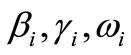 and
and , we will use equations (26)-(28) in the following forms
, we will use equations (26)-(28) in the following forms
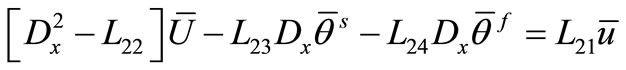 , (42)
, (42)
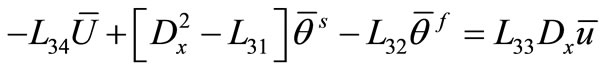 , (43)
, (43)
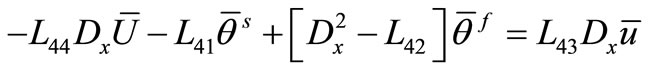 , (44)
, (44)
Inserting the formulas in (37)-(40) into equations (42)-(44), we get
 , (45)
, (45)
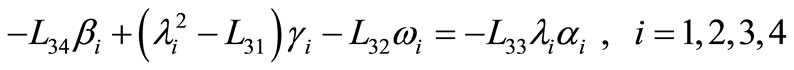 , (46)
, (46)
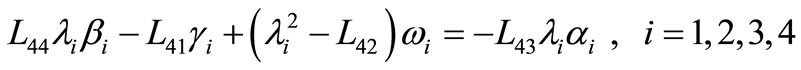 , (47)
, (47)
By solving the system in (45)-(47), we obtain
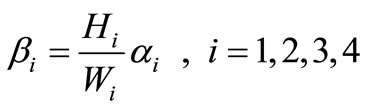 ,
,
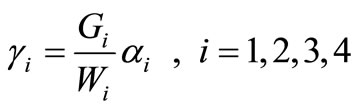 ,
,
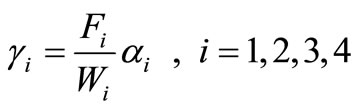
where
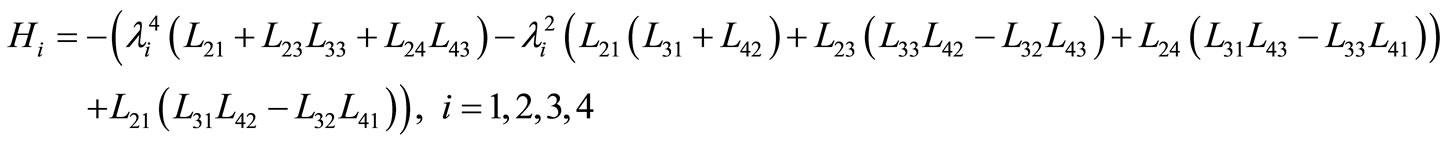

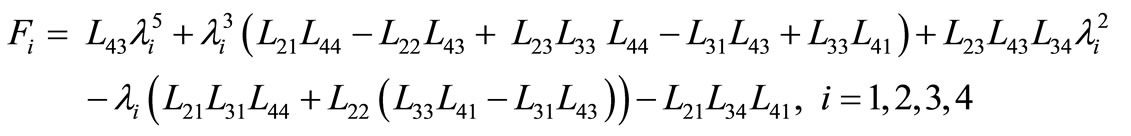
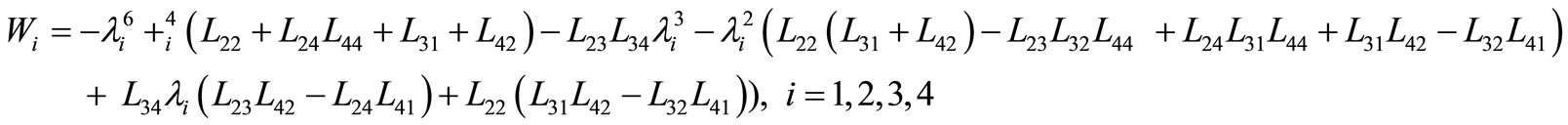
Hence, we have
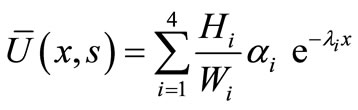 , (48)
, (48)
 , (49)
, (49)
 , (50)
, (50)
To get the values of the parameters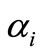 , we have to apply the boundary conditions as follows;
, we have to apply the boundary conditions as follows;
1) The thermal conditions We will consider the bounding plane surface of the medium at x = 0 has been thermally loaded by thermal shock as follows:
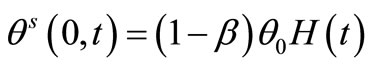 , (51)
, (51)
and
 , (52)
, (52)
where H(t) is the Heaviside unite step function and 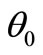 is constant which gives after using the Laplace transform the following conditions
is constant which gives after using the Laplace transform the following conditions
 , (53)
, (53)
and
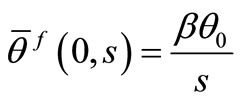 , (54)
, (54)
2) The mechanical conditions We will consider the bounding plane surface of the medium at x = 0 has been connected to a rigid surface which prevents any displacement to accrue on that surface, i.e.,
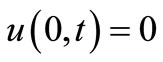 , (55)
, (55)
and
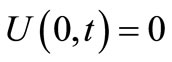 , (56)
, (56)
which gives after using the Laplace transform the following conditions
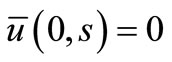 , (57)
, (57)
and
 . (58)
. (58)
After using the boundary conditions in (53), (54), (57) and (58), we get the following system
 , (59)
, (59)
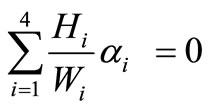 , (60)
, (60)
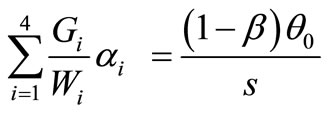 , (61)
, (61)
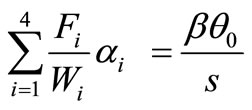 , (62)
, (62)
Then we get
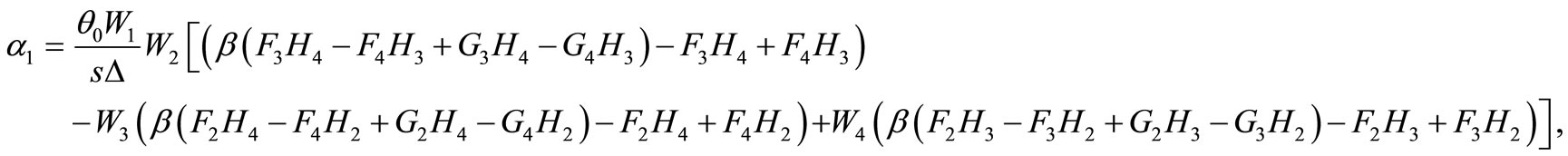



where
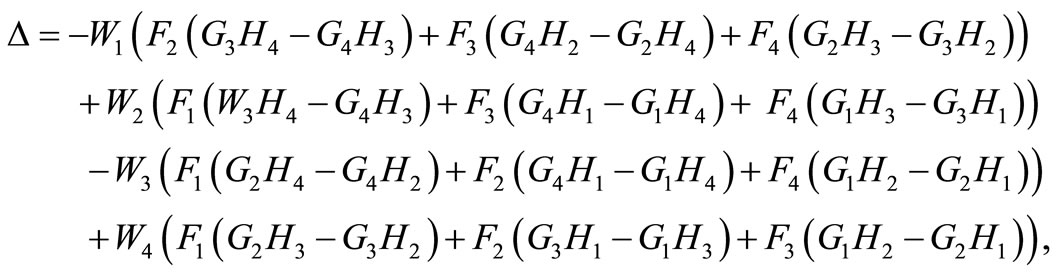
Those complete the solution in the Laplace transform domain.
5. Numerical Inversion of the Laplace Transforms
In order to invert the Laplace transforms, we adopt a numerical inversion method based on a Fourier series expansion [27].
By this method the inverse 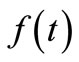 of the Laplace transform
of the Laplace transform 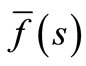 is approximated by
is approximated by
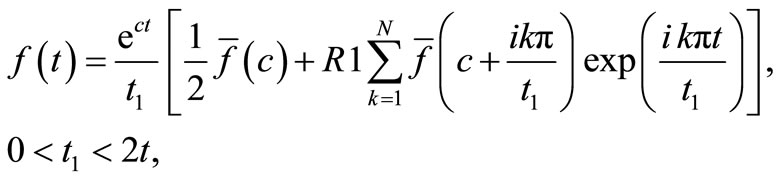
where N is a sufficiently large integer representing the number of terms in the truncated Fourier series, chosen such that
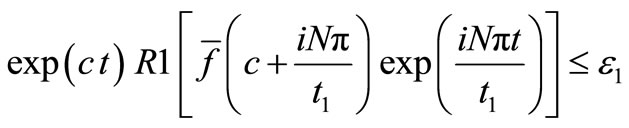
where e1 is a prescribed small positive number that corresponds to the degree of accuracy required. The parameter c is a positive free parameter that must be greater than the real part of all the singularities of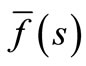 . The optimal choice of c was obtained according to the criteria described in [27].
. The optimal choice of c was obtained according to the criteria described in [27].
6. Numerical Results and Discussion
The Ferrari’s method has been constructed by using the FORTRAN program to solve Equation (41). The material properties of asphaltic material saturated by water have been taken as follow [28,29].

Figure 1. Asphalt temperature distribution.

Figure 2. Water temperature distribution.
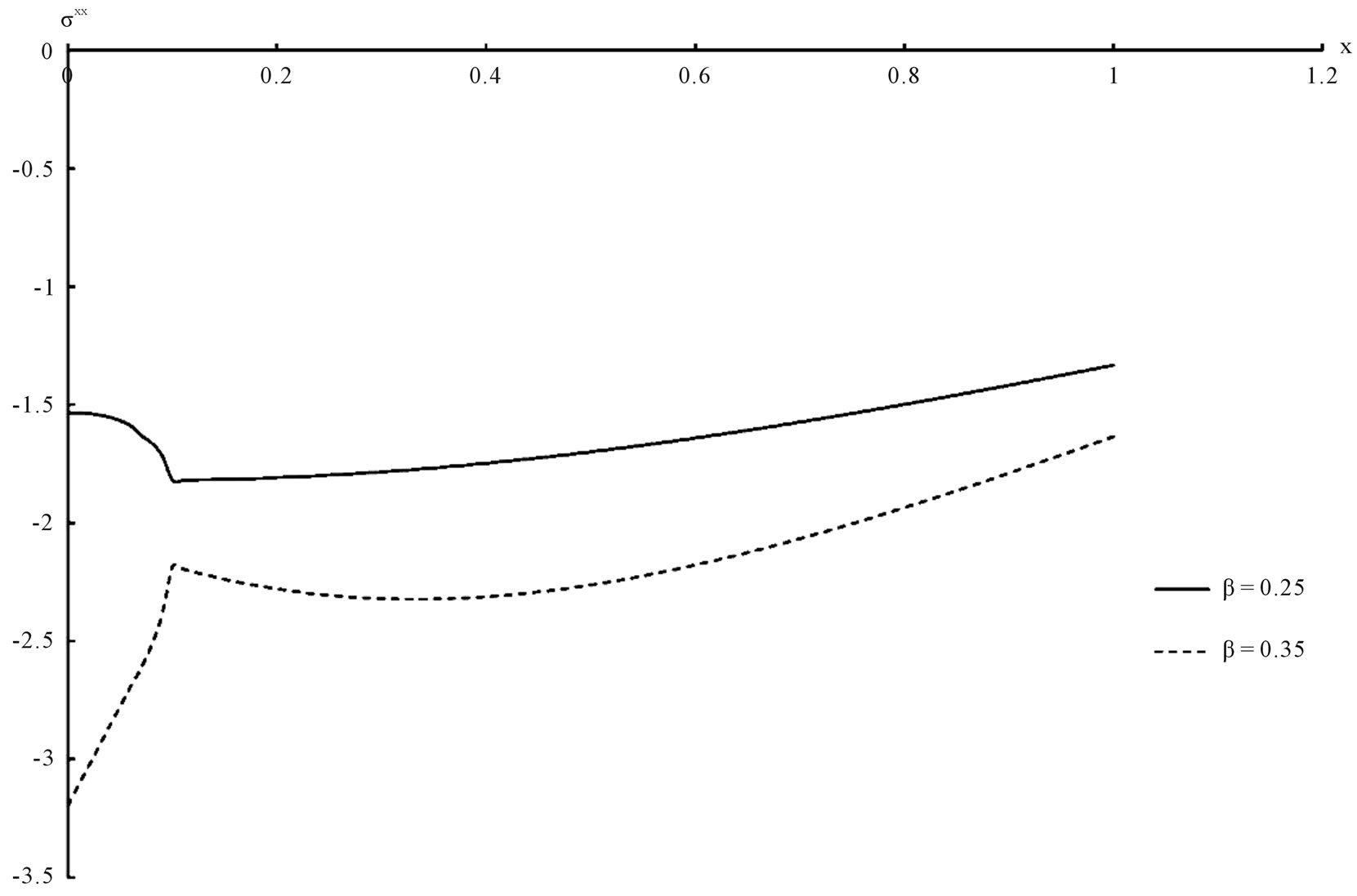
Figure 3. Asphalt stress distribution.

Figure 4. Water stress distribution.
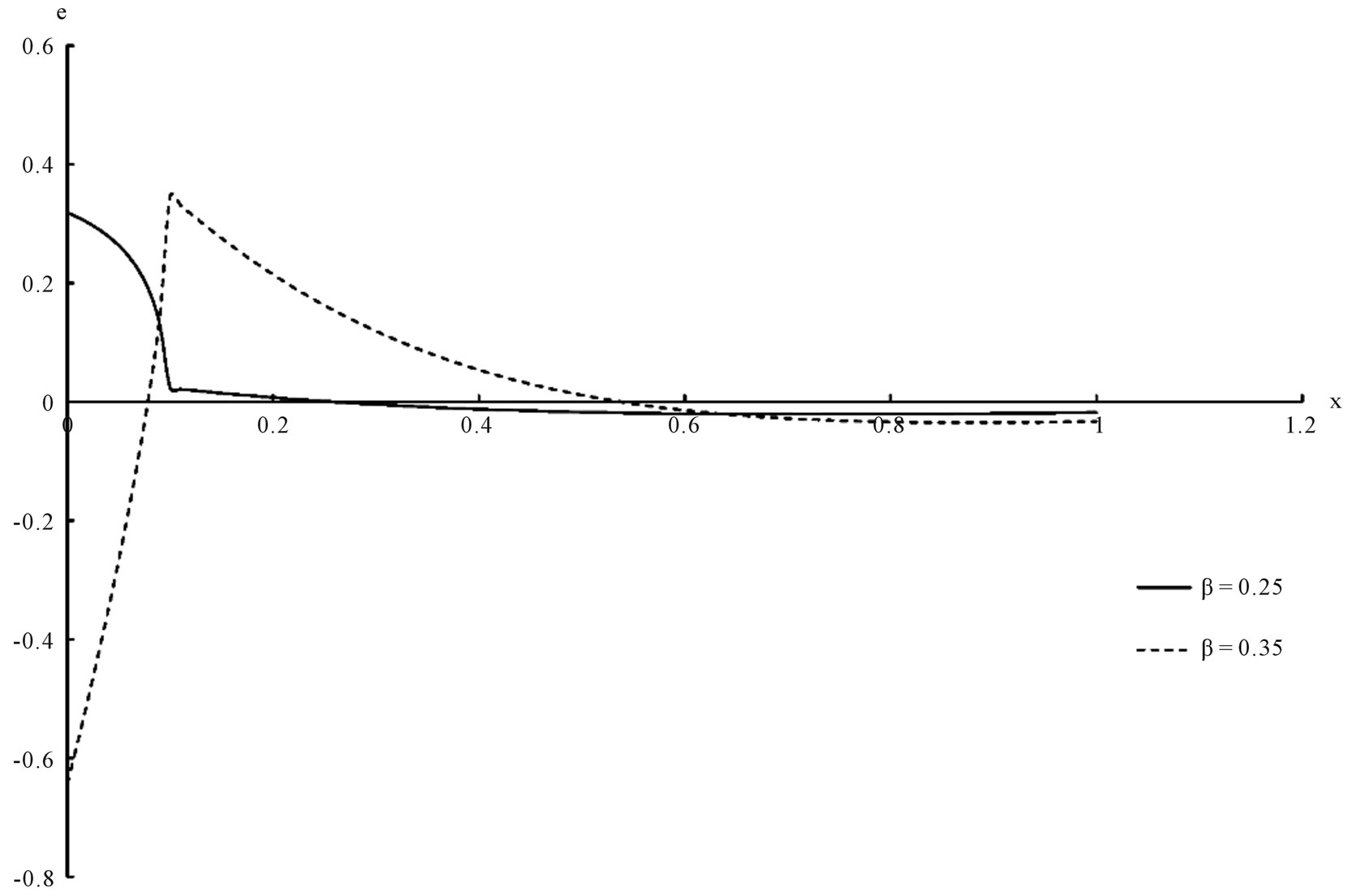
Figure 5. Asphalt strain distribution.

Figure 6. Water strain distribution.
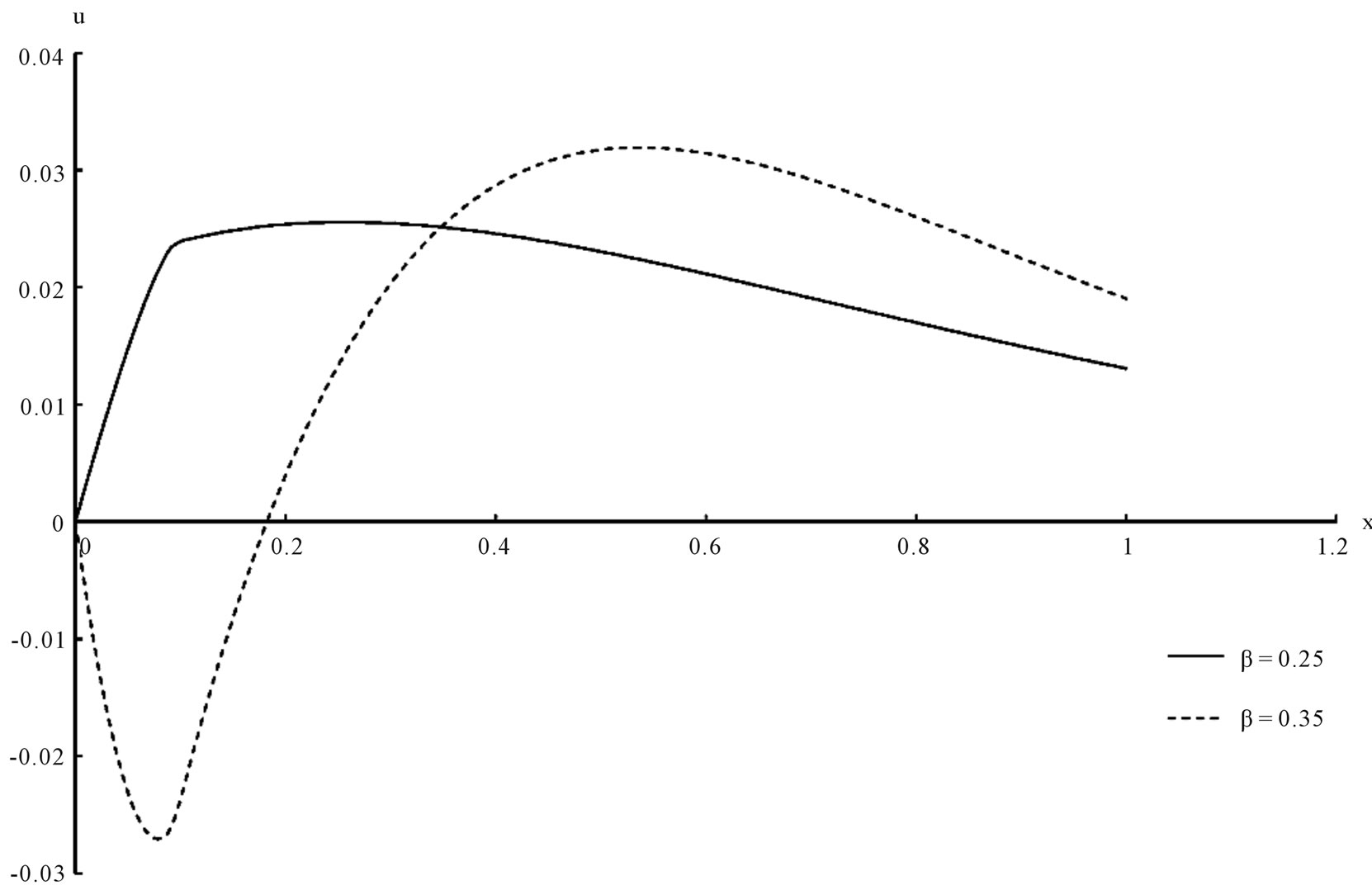
Figure 7. Asphalt displacement distribution.
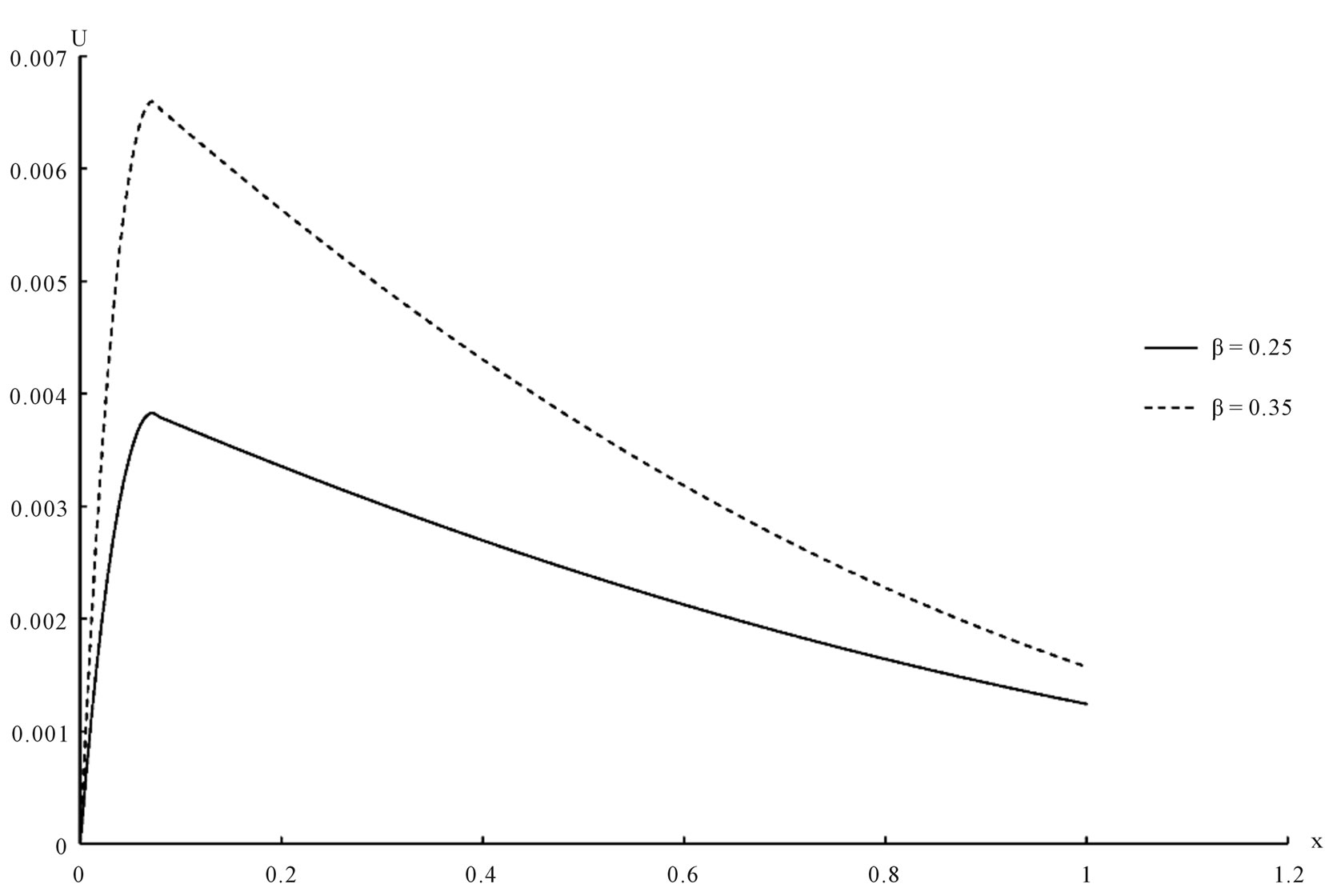
Figure 8. Water displacement distribution.
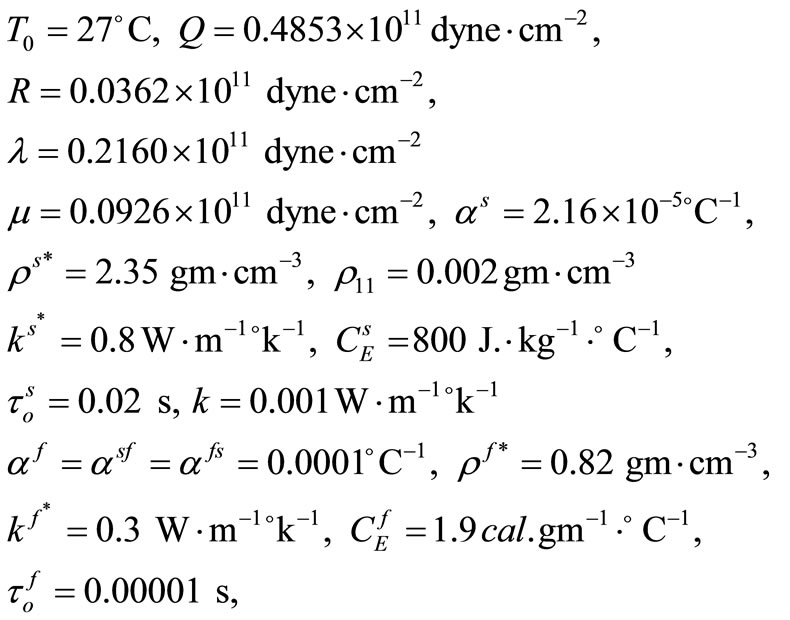
We will take the non-dimensional x variable to be in interval 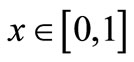 and all the results will be calculated at the same instance
and all the results will be calculated at the same instance  for two different values of the porosity
for two different values of the porosity  of the material when
of the material when 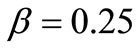 and
and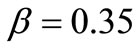 .
.
The temperature, the stress, the strain and the displacement for the solid and the liquid have been shown in figures 1-8 respectively. We can see that, the value of the porosity has a significant effect on all the studied fields.
7. Conclusions
This work was dealing with studying the effect of the porosity of isotropic and poroelastic one dimensional half-space which is saturated with fluid. The mathematical model of generalized porothermoelasticity with one relaxation time has been constructed in the context of Youssef model. The general solution has been obtained in the Laplace transform domain and applied it in a certain asphalt material which is thermally shocked on its bounding plane. The inversion of the Laplace transform has been obtained numerically and the numerical values of the temperature, stresses, strains and displacements have been presented graphically for the solid and the liquid and the graphs shown the significant effect of the porosity value.
8. REFERENCES
- C. Pecker and H. Deresiewiez, “Thermal Effects on Wave in Liquid-Filled Porous Media,” Journal of Acta Mechanica, Vol. 16, No. 1-2, 1973, pp. 45-64. doi:10.1007/BF01177125
- M. A. Biot, “General Theory of Three-Dimensional Consolidation,” Journal of Applied Physics, Vol. 12, No. 2, 1941, pp. 155-164. doi:10.1063/1.1712886
- M. A. Biot, “Theory of Propagation of Elastic Waves in a Fluid-Saturated Porous Solid. I. Low-Frequency Range,” Journal of Acoustical Society America, Vol. 28, No. 2, 1956, pp. 168-178. doi:10.1121/1.1908239
- F. Gassmann, “Uber die Elastizitat Poroser Medien,” Veirteljahrsschrift der Naturforschenden Gesellschaft in Zzirich, Vol. 96, 1951, pp. 1-23.
- M. A. Biot and D. G. Willis, “The Elastic Coefficients of the Theory of Consolidation,” Journal of Applied Mechanics, Vol. 24, No. 4, 1957, pp. 594-601.
- M. A. Biot, “Mechanics of Deformation and Acoustic Propagation in Porous Media,” Journal of Applied Physics, Vol. 33, No. 4, 1962, pp. 1482-1498. doi:10.1063/1.1728759
- H. Deresiewicz and R. Skalak, “On Uniqueness in Dynamic Poroelasticity,” Bulletin of the Seismological Society of America, Vol. 53, No. 4, 1963, pp. 783-788.
- G. Mandl, “Change in Skeletal Volume of a Fluid-Filled Porous Body under Stress,” Journal of Applied Physics, Vol. 12, No. 5, 1964, pp. 299-315. doi:10.1016/0022-5096(64)90027-4
- A. Nur and J. D. Byerlee, “An Exact Effective Stress Law for Elastic Deformation of Rock with Fluids,” Journal of Geophysical Research, Vol. 76, No. 26, 1971, pp. 6414- 6419. doi:10.1029/JB076i026p06414
- R. J. S. Brown and J. Korringa, “On the Dependence of the Elastic Properties of a Porous Rock on the Compressibility of the Pore Fluid,” Geophysics, Vol. 40, 1975, pp. 608-616. doi:10.1190/1.1440551
- J. R. Rice and M. P. Cleary, “Some Basic, Stress Diffusion Solutions for Fluid-Saturated Elastic Porous Media with Compressible Constituents,” Review of Geophysics, Space Physics, Vol. 14, No. 2, 1976, pp. 227-241. doi:10.1029/RG014i002p00227
- R. Burridge and J. B. Keller, “Poroelasticit, y Equations Derived from Microstructure,” Journal of Acoustical Society America, Vol. 70, No. 4, 1981, pp. 1140-1146. doi:10.1121/1.386945
- R. W. Zimmerman, W. H. Somerton and M. S. King, “Compressibility of Porous Rocks,” Journal of Geophysical Research, Vol. 91, No. B12, 1986, pp. 12765- 12777. doi:10.1029/JB091iB12p12765
- R. W. Zimmerman, L. R. Myer and N. G. W. Cook, “Grain and Void Compression in Fractured and Porous Rock,” International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, Vol. 31, No. 2, 1994, pp. 179-184. doi:10.1016/0148-9062(94)92809-6
- J. G. Berryman and G. W. Milton, “Exact Results for Generalized Gassmann’s Equations in Composite Porous Media with Two Constituents,” Geophysics, Vol. 56, 1991, pp. 1950-1960. doi:10.1190/1.1443006
- M. Thompson and J. R. Willis, “A Reformation of the Equations of Anisotropic Poroelasticity,” Journal of Applied Mechanics, Vol. 58, No. 3, 1991, pp. 612-616. doi:10.1115/1.2897239
- S. R. Pride, A. F. Gangi and F. D. Morgan, “Deriving the Equations of Motion for Porous Isotropic Media,” Journal of Acoustical Society America, Vol. 92, No. 6, 1992, pp. 3278-3290. doi:10.1121/1.404178
- J. G. Berryman and H. F. Wang, “The Elastic Coefficients of Double-Porosity Models for Fluid Transport in Jointed Rock,” Journal of Geophysical Research, Vol. 100, No. B12, 1995, pp. 24611-24627. doi:10.1029/95JB02161
- K. Tuncay and M. Y. Corapcioglu, “Effective Stress Principle for Saturated Fractured Porous Media,” Water Resources Research, Vol. 31, No. 12, 1995, pp. 3103-3106. doi:10.1029/95WR02764
- A. H. D. Cheng, “Integral Equation for Poroelasticity in Frequency Domain with BEM solution,” Journal of Engineering Mechanics, Vol. 117, No. 5, 1991, pp. 1136- 1157. doi:10.1061/(ASCE)0733-9399(1991)117:5(1136)
- P. A.Charlez and O. Heugas, “Measurement of Thermoporoelastic Properties of Rocks: Theory and Applications,” In: J. A. Hudson, Ed., International Society for Rock Mechanics, Tour Total, Paris, 1992, pp. 42-46.
- Y. Abousleiman and L. Cui, “Poroelastic Solutions in Transversely Isotropic Media for Wellbore and Cylinder,” International Journal of Solids Structures, Vol. 35, No. 34-35, 1998, pp. 4905-4903. doi:10.1016/S0020-7683(98)00101-2
- A. Ghassemi and A. Diek, “Porothermoelasticity for Swelling Shales,” Journal of Petroleum Science & Engineeing, Vol. 34, 2002, pp. 123-135.
- S. R. Tod, “An Anisotropic Fractured Poroelastic Effective Medium Theory,” Geophysical Journal International, Vol. 155, No. 3, 2003, pp. 1006-1020.
- H. Lord and Y. Shulman, “A Generalized Dynamical Theory of Thermoelasticity,” Journal of the Mechanics and Physics of Solids, Vol. 15, No. 5, 1967, pp. 299-309. doi:10.1016/0022-5096(67)90024-5
- H. M. Youssef, “Theory of Generalized Porothermoelasticity,” International Journal of Rock Mechanics and Mining Sciences, Vol. 44, No. 2, 2007, pp. 222-227. doi:10.1016/j.ijrmms.2006.07.001
- G. Honig and U. Hirdes, “A Method for the Numerical Inversion of Laplace Transform,” Journal of Computational and Applied Mathematics, vol. 10, No. 1, 1984, pp. 113-132. doi:10.1016/0377-0427(84)90075-X
- G.-B. Liu, S.-R. Ding, R.-H. Ye and X.-H. Liu, “Relaxation Effects of a Saturated Porous Media Using the TwoDimensional Generalized Thermoelastic Theory,” Transport in Porous Media, Vol. 86, No. 1, 2011, pp. 283-303. doi:10.1007/s11242-010-9621-9
- Y. Zhong and L. Geng, “Thermal Stresses of Asphalt Pavement under Dependence of Material Characteristics on Reference Temperature,” Mechanics of Time-Dependent Materials, vol. 13, No. 1, 2009, pp. 81-91. doi:10.1007/s11043-008-9073-6
Nomenclature
 The displacements of the skeleton and fluid phases
The displacements of the skeleton and fluid phases
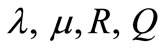 The poroelastic coefficients
The poroelastic coefficients
 The mixed and thermal coefficients
The mixed and thermal coefficients
 The temperature increment of the solid where
The temperature increment of the solid where 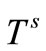 is the solid
is the solid
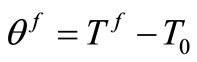 The temperature increment of the fluid where
The temperature increment of the fluid where 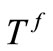 is the fluid
is the fluid
 The reference temperature
The reference temperature
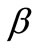 The porosity of the material
The porosity of the material
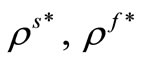 The density of the solid and the liquid phases respectively
The density of the solid and the liquid phases respectively
 The density of the solid phase per unit volume of bulk
The density of the solid phase per unit volume of bulk
 The density of the solid phase per unit volume of bulk
The density of the solid phase per unit volume of bulk
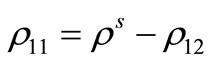 The mass coefficient of solid phase
The mass coefficient of solid phase
 The mass coefficient of fluid phase
The mass coefficient of fluid phase
 The dynamics coupling coefficient
The dynamics coupling coefficient
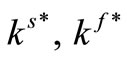 The thermal conductivity of the solid and the fluid phases
The thermal conductivity of the solid and the fluid phases
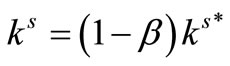 The thermal conductivity of the solid phase
The thermal conductivity of the solid phase
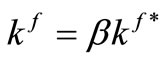 The thermal conductivity of the fluid phase k The interface thermal conductivity
The thermal conductivity of the fluid phase k The interface thermal conductivity
 The relaxation time of the solid and the fluid phases
The relaxation time of the solid and the fluid phases
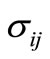 The stress components apply to the solid surface
The stress components apply to the solid surface
 The normal stress apply to the fluid surface
The normal stress apply to the fluid surface
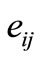 The strain component of the solid phase
The strain component of the solid phase
 The strain component of the fluid phase
The strain component of the fluid phase
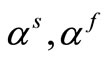 The coefficients of the thermal expansion of the phases
The coefficients of the thermal expansion of the phases
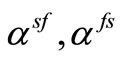 The thermoelastic couplings between the phases
The thermoelastic couplings between the phases
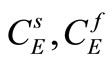 The specific heat of the solid and the fluid phases
The specific heat of the solid and the fluid phases
 The specific heat couplings between the phases
The specific heat couplings between the phases
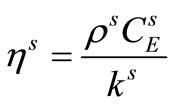 The thermal viscosity of the solid
The thermal viscosity of the solid
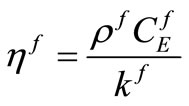 The thermal viscosity of the fluid
The thermal viscosity of the fluid
 The thermal viscosity couplings between the phases
The thermal viscosity couplings between the phases