Engineering
Vol. 3 No. 12 (2011) , Article ID: 9210 , 5 pages DOI:10.4236/eng.2011.312148
DNAPL Infiltration in a Two-Dimensional Porous Medium—Influence of the Shape of the Solid Particles
European University of Brittany, LGCGM-INSA, Rennes, France
E-mail: Mustapha.Hellou@insa-rennes.fr
Received August 9, 2011; revised October 1, 2011; accepted October 15, 2011
Keywords: DNAPL, Multiphase Flow, Wetting Liquid, Solid Particle, VOF, Retention of Liquid Pollutant
ABSTRACT
The infiltration with atmospheric pressure of Dense Non Aqueous Phase Liquid (DNAPL) in a model of porous medium saturated by another liquid is studied when this DNAPL liquid has a contact angle characterizing wetting liquid. The model of the porous medium considered consists of an assembly of solid particles for various forms. The influence of the shape of the particles is studied. The results found show the retention capacity of such porous media in function of the shape of the solid particles.
1. Introduction
Multiphase flows in porous media involving immiscible fluids always interest scientists in terms of applied and fundamental point of view. For example, the transport of immiscible fluid with water known as NAPL (Non Aqueous Phase Liquid) is encountered in geomaterials, processes of remediation of the grounds, biofilters employed in waste water treatment, etc. These flows are complex and often unknown because of the large number of physical parameters involved to describe their properties. At the present time, influence of parameters as density, viscosity or nterfacial tension on the infiltration of NAPL into porous media is much studied by several authors [1-6]. Most of these studies are realized at a macroscopic scale. This macroscopic approach does not make it possible to understand the retention of small drops of DNAPL (Dense Non Aqueous Phase Liquid) in the pores of the medium. However, few studies carried out at the scale of the interstices showed the dispersion of the DNAPL as well in experiments and in numerical simulation [7-9].
In this work, we highlight the influence of a parameter which is poorly studied—geometry of the solid particles of porous media—on the infiltration and the dispersion of a drop of DNAPL. Numerical simulation is carried out for various shapes of the solid particles.
2. Problem Position
The fluids used in this study are water (carrier fluid) and the DNAPL (the drop). The density and the viscosity of water are of 998 kg·m–3 and 1 × 10–3 Pa·s. Those of the DNAPL are respectively equal to 1623 kg·m–3 and 0.89 Pa·s. As an example, Perchlorethylen (PCE) possesses similar properties (INERIS, 2002). A contact angle of 65˚ is imposed in order to consider a wetting DNAPL because most DNAPL’s being in nature are wetting.
Figure 1 presents one of the three structures of porous
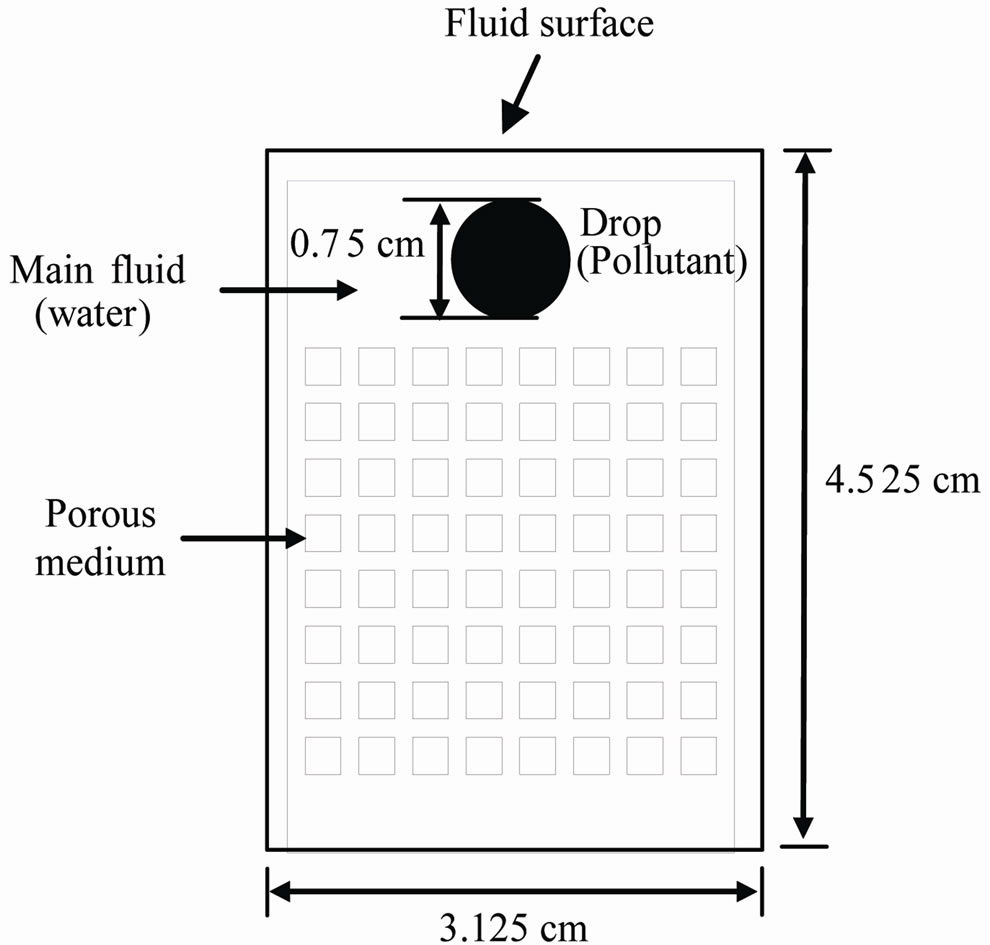
Figure 1. Description of the computational domain case m →∞. The gap between two particles is equal to 0.125 cm.
medium used. This porous medium is represented by a periodic assemblage of similar and non deformable solid particles. The circle outside the medium represents a drop of DNAPL at the initial time. It is injected without initial velocity within the carrying fluid which is at rest. Under the effect of gravity the dense drop infiltrates downward through the porous medium. The domain of calculation is rectangular. Its dimensions relative to the radius R of a solid particle are 12.5 × 18.1 and it is composed of 3 zones. From top to bottom, zone1 contains the drop at t = 0, zone 2 contains the porous medium composed by 64 particles, zone 3 contains the wall of the bottom which is used to recover the infiltrated DNAPL.
The shape of a solid particle is described by the following equation which enables us to pass from the circular form to the almost square form by increasing the value of the parameter m:
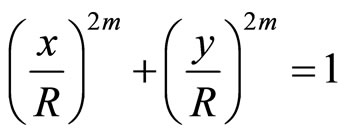 (1)
(1)
In this paper, we present three models of periodic porous media which differ by the form of the solid particles by varying m: m = 1 (circle), m = 2 and m→∞ (square). In order to conserve the same porosity (0.36), we vary the side of the square mesh (see Figure 2) while preserving R constant.
The gap between two particles is equal to 0.125 cm.
In this study, we use a numerical simulation based on VOF model (Volume of Fluid) [10]. When solving the Navier-Stokes equation for each fluid, these two authors introduced the definition of the volume fraction 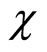 of the immiscible fluids (1 and 2) into the mesh. The volume fraction is equal to 0 in fluid 1, equal to 1 in fluid 2 or between 0 and 1 within the interface of the fluids. Here fluid 1 is the main fluid. The volume fraction in a point of velocity
of the immiscible fluids (1 and 2) into the mesh. The volume fraction is equal to 0 in fluid 1, equal to 1 in fluid 2 or between 0 and 1 within the interface of the fluids. Here fluid 1 is the main fluid. The volume fraction in a point of velocity 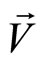 on the interface is controlled by the following equation:
on the interface is controlled by the following equation:
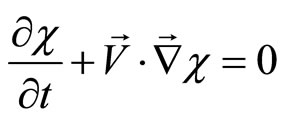 (2)
(2)
Equation of Navier Stokes for each fluid is given by the following expression:
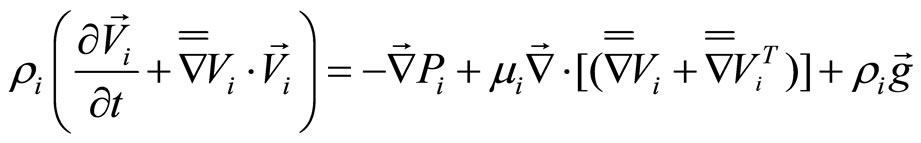 (3)
(3)
where Pi is the pressure in the fluid i. The operators and
and 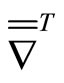 represent the gradient tensor and the transpose gradient tensor. The resolution of these equations has been realized by a computational fluid dynamics package (COMSOL Multiphysics). The solution takes into account the behaviour on the interface represented by Equation (2) and the boundary conditions that are: adherence on all the solid surfaces and a pressure constant on the fluid surface. The validation of the results has been conducted by comparison with experiments.
represent the gradient tensor and the transpose gradient tensor. The resolution of these equations has been realized by a computational fluid dynamics package (COMSOL Multiphysics). The solution takes into account the behaviour on the interface represented by Equation (2) and the boundary conditions that are: adherence on all the solid surfaces and a pressure constant on the fluid surface. The validation of the results has been conducted by comparison with experiments.
3. Results and Discussion
Before presenting the results for infiltration of DNAPL in various models of porous media, we proceeded to validate the computational code. Thus Figure 3 compare experimental results realized in LGCGM with numerical results obtained by VOF Model. The experiments concern the infiltration of a drop in a porous medium formed by glass cylinders. Despite the three dimensional drop, the experimental results are in good agreement with numerical ones. These results confirm the validity of the numerical calculation.
Figure 4 shows the infiltration of a drop into each of the models presented in Figure 2. The results are presented in function of time. For generalization, time can be normalized by the time of settling of the drop in an infinite static continuous flow field. The settling velocity found by [12,13] is:
 (4)
(4)

Figure 2. Shape of the solid particles. R = 0.125 cm.

Figure 3. Experimental and numerical visualization of infiltration of a DNAPL in a porous medium [11].
where 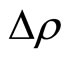 is the difference of densities,
is the difference of densities, 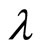 is the ratio of the drop viscosity and the continuous fluid viscosity,
is the ratio of the drop viscosity and the continuous fluid viscosity, 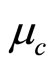 is the viscosity of the continuous fluid. For water as continuous fluid and PCE as the drop, the value of the settling velocity is 31.7 mm·s−1, the reference time is thus t0 = d/Ud∞ = 0.24 s.
is the viscosity of the continuous fluid. For water as continuous fluid and PCE as the drop, the value of the settling velocity is 31.7 mm·s−1, the reference time is thus t0 = d/Ud∞ = 0.24 s.
The infiltration of DNAPL in porous medium is complex even if the medium of Figure 4 is perfectly periodic. Thus, Figure 4 illustrates that the injected drop spreads out horizontally immediately before infiltrating vertically into the porous medium.The drop tries to maintain its surface constant but the more deeply it infiltrates, the more it is divided into several droplets. By comparing the infiltration in these three models, we note that when m increases, division of the principal drop onto droplets is more important. The position of these droplets retained in the medium is not predicable. However, the infiltration of DNAPL in the medium formed by square particle, presents less dispersion relatively to the medium formed by circular particles.
The specific surface (surface of the solid particles per unit of volume of porous material) is related to the porosity n by the following equations:
Circle:  (5)
(5)
Square:  (6)
(6)
For the same porosity, the specific surface for the square is twice the specific surface in the case of circles. It’s a part of explanation of the greatest retention observed for the square particles.
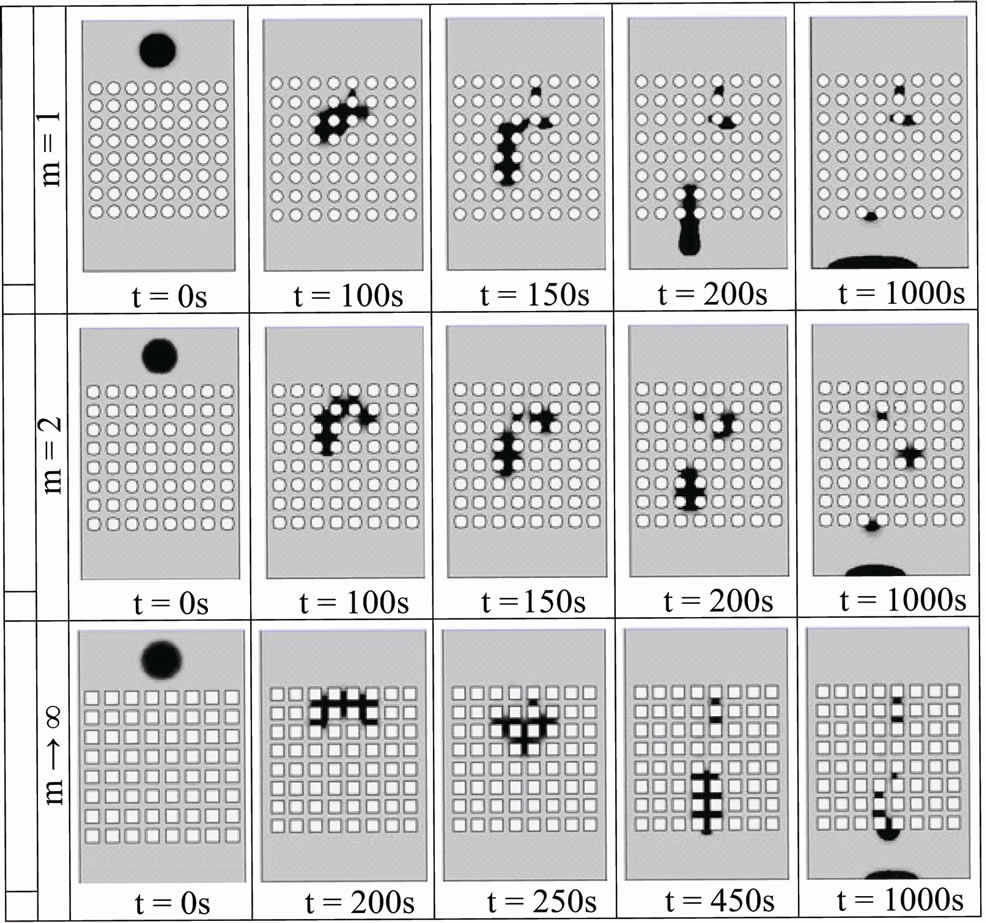
Figure 4. Tracking of a DNAPL drop during its infiltration in a model of porous medium.
Figure 5 explains the mechanism of retention of the droplets in contact with two solid particles of a horizontal row. We note that surface of the liquid/solid contact increases with increasing the parameter m. This surface is minimum for the case where the solid particles are circles. The more surface of the liquid/solid contact increases, the more adherence on the area of this contact increases. This explains why the drops are retained between the solid particles with increasingly large volume as m increases.
In Figure 5 we have presented the contact forces and their direction taking into account that the drop is composed by a wetting fluid. In this condition, the contact forces are opposed to the apparent weight. Thus the vertical components of these contact forces are responsible to the retention when their sum is greater than the apparent weight. Due to the solid surface inclination, the vertical components are greater for the square compared to the circles. The consequence is that the volume retained between the square particles can be greater than the volume retained by the circular particles.
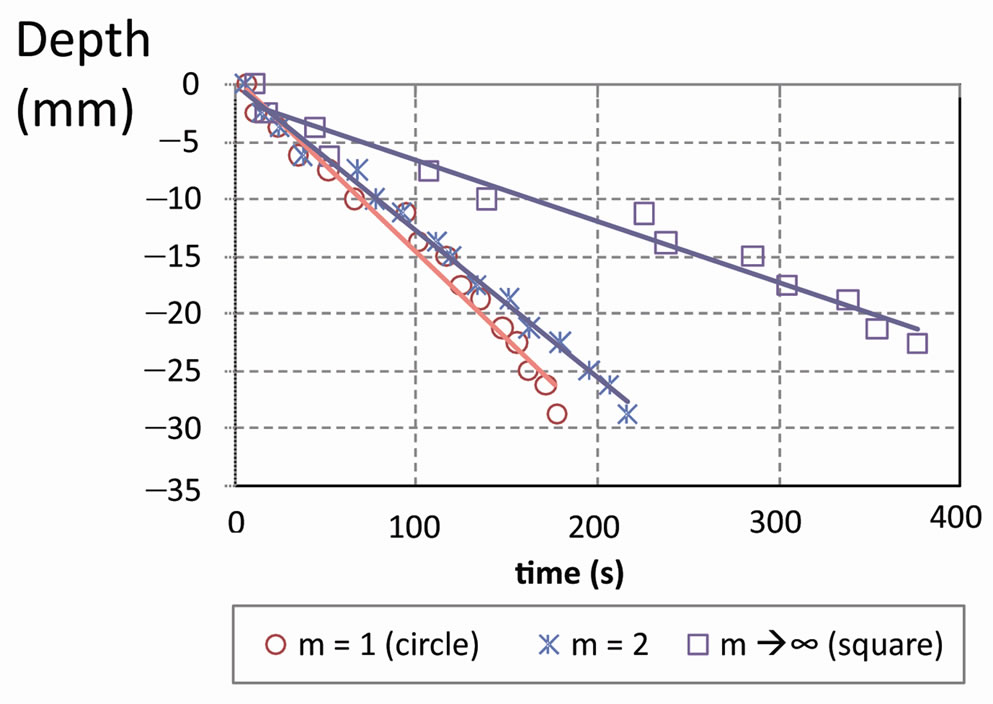
Then we compare then the velocity of the DNAPL infiltration into different models of porous media. For each model, calculation is carried out until the drop becomes at rest. We present in Figure 6(a) the depth of the infiltration (vertical position of the lower face of the drop relatively to the upper surface of the porous medium) according to time for the three models. We find that the velocity of the infiltration of DNAPL decreases when m increases. Figure 6(b) shows the volume of retention of DNAPL in the different models of the porous medium. The parameter 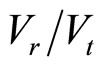 defines the ratio of the volume of DNAPL retained in the medium on the total volume of DNAPL injected. In the case of the particles having the circular form, most of the drop passes through the porous medium. There is only 30% of the volume of the drop retained in the pores. When the shape of the particles tends towards the square form, the volume of DNAPL retained in the pores increases and reaches 64% and 72% respectively for the case m = 2 and the case of the square.
defines the ratio of the volume of DNAPL retained in the medium on the total volume of DNAPL injected. In the case of the particles having the circular form, most of the drop passes through the porous medium. There is only 30% of the volume of the drop retained in the pores. When the shape of the particles tends towards the square form, the volume of DNAPL retained in the pores increases and reaches 64% and 72% respectively for the case m = 2 and the case of the square.

 represents the contact force;
represents the contact force;  represents the apparent weight of the drop.
represents the apparent weight of the drop.
Figure 5. Illustration of the mechanism of drop retention.
 (a)
(a)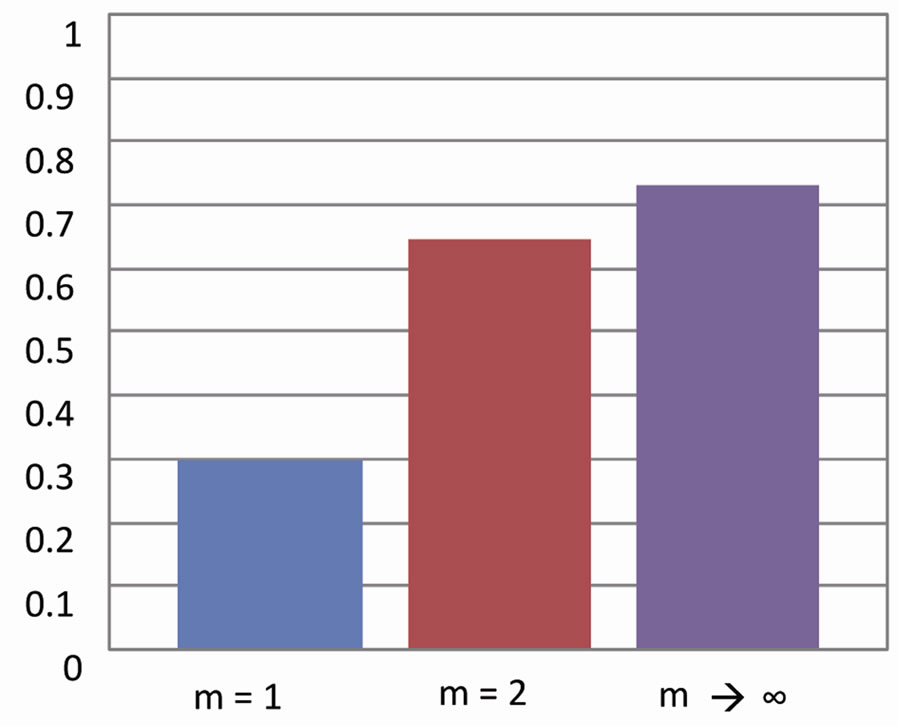 (b)
(b)
Figure 6. (a) DNAPL infiltration depth in function of time; (b) DNAPL retention volume (ratio of the volume of DNAPL retained in the medium and the total volume of DNAPL injected).
4. Conclusions
The analysis of the influence of the shape of the solid particles on the infiltration of the DNAPL is carried out for several forms: circular, square, intermediate form between the circle and the square. This study highlights that as the shape of the particles passes from the circle shape to the square shape, the solid specific surface increases, the velocity of infiltration decreases and the retention of DNAPL increases. This retention is the result of division of the drop.
This study has been conducted for the same porosity of the three models of porous media corresponding to three shapes of solid particles. It could be interesting to do a similar study but for the same specific solid surface (i.e. the same available surface of contact) in order to complete the knowledge the relative influence of the shape of the solid particles on the infiltration of DNAPL into porous media.
5. REFERENCES
- K. D. Pennell, G. A. Pope and L. M. Abriola, “Influence of Viscous and Buoyancy Forces on the Mobilization of Residual Tetrachloroethylene during Surfactant Flushing,” Environmental Science & Technology, Vol. 30, No. 4, 1996, pp. 1328-1335. doi:10.1021/es9505311
- H. E. Dawson and P. V. Roberts, “Influence of Viscous, Gravitational, and Capillary Forces on DNAPL Saturation,” Ground Water, Vol. 35, No. 2, 1997, pp. 261-269. doi:10.1111/j.1745-6584.1997.tb00083.x
- C. Hofstee, C. G. Ziegler, O. Trötschler and J. Braun, “Removal of DNAPL Contamination from the Saturated Zone by the Combined Effect of Vertical Upward Flushing and Density Reduction,” Journal of Contaminant Hydrology, Vol. 67, No. 1, 2003, pp. 61-78. doi:10.1016/S0169-7722(03)00088-3
- S. W. Jeong and M.-Y. Corapcioglu, “Force Analysis and Visualization of NAPL Removal during Surfactant-Related Floods in a Porous Medium,” Journal of Hazardous Materials, Vol. A126, 2005, pp. 8-13. doi:10.1016/j.jhazmat.2005.06.015
- A. M. Tartakovsky, A. L. Ward and P. Meakin, “Heterogeneity Effects on Capillary Pressure-Saturation Relations Inferred from Pore-Scale Modeling,” Physics of Fluids, Vol. 19, 2007, Article ID: 103301.
- P. Meakin and A. M. Tartakovsky, “Modeling and Simulation of Pore Scale Multiphase Fluid Flow and Reactive Transport in Fractured and Porous Media,” Reviews of Geophysics, Vol. 47, 2009, Article ID: RG3002. doi:10.1029/2008RG000263
- R. Krishna and J. M. Van Baten, “Rise Characteristics of Gaz Bubbles in a 2D Rectangular Column: VOF Simulations vs Experiments,” International Communications in Heat and Mass Transfer, Vol. 66, No. 7, 1999, pp. 965- 974. doi:10.1016/S0735-1933(99)00086-X
- G. J. Storr and M. Behnia, “Comparisons between Experiment and Numerical Simulation Using a Free Surface Technique of Free-Falling Liquid Jets,” Experimental Thermal and Fluid Science, Vol. 22, No. 1-2, 2000, pp. 79-91. doi:10.1016/S0894-1777(00)00013-3
- D. J. E. Harvie, M. R. Davidson, J. J. Cooper-White and M. Rudman, “A Parametric Study of Droplet Deformation through a Microfluidic Contraction: Low Viscosity Newtonian Droplets,” Chemical Engineering Science, Vol. 61, No. 15, 2006, pp. 5149-5158. doi:10.1016/j.ces.2006.03.011
- C. W. Hirt and B. D. Nichols, “Volume of Fluid (VOF) Method for the Dynamics of Free Boundaries,” Journal of Computational Physics, Vol. 39, 1981, pp. 201-225. doi:10.1016/0021-9991(81)90145-5
- T. D. Nguyen, “Infiltration de Particules Liquids ou Solides dans un Milieu Poreux,” Ph.D. Thesis, INSA, Rennes, 2007.
- J. S. Hadamard, “Mouvement Permanent Lent d’une Sphère Liquide et Visqueuse dans un Liquide Visqueux,” Comptes Rendus de l’Académie des Sciences, Vol. 152, 1911, pp. 1735-1752.
- W. Rybczynski, “On the Translatory Motion of a Fluid Sphere in a Viscous Medium,” Bull. Acad. Sci., Series A, Cracow, 1911, p. 40.

