Engineering
Vol. 3 No. 10 (2011) , Article ID: 8083 , 4 pages DOI:10.4236/eng.2011.310126
Influence of Structural Aspects on the Generation Process in Planetary Gear Trains
JITSW, Hanamkonda, Bits-Pilani, Hyderabad, India
E-mail: rajasrii331@gmail.com, avs_gupta@rediffmail.com, yvdrao@yahoo.com
Received July 21, 2011; revised August 10, 2011; accepted August 20, 2011
Keywords: Planetary Gear Trains, Generation Process of PGTs, Isomorphism, Symmetry, Structural Arrangements, Hamming Matrix
ABSTRACT
Structural and rotational isomorphism in planetary Gear Trains (PGTs), is tested by Hamm-ing number method. Symmetry in PGTs can be determined from the same Hamming matrix. Bearing of the structural property like symmetry in PGTs is studied and is used to evaluate its influence on generation of PGTs.
1. Introduction
Structural synthesis and analysis of mechanisms plays an important role in the investigation for mechanisms. Identification of isomorphism among various PGTs of given number of links and Degree of freedom (DOF) is very important in synthesis process. PGTS are preferred because of its advantages like high speed reduction, light weight, compactness and capability of differential drive. PGTS are used in applications like gear boxes of machine tool, robots etc. to transmit specified motion and torque between two or more shafts.
Generation of PGTs is also one of the important stages in synthesis of gear train and in an “n” link PGT, there are (n-2) gear pairs and (n-1) turning pairs [1,2]. Gear pairs are denoted by thick lines and turning pair is represented by thin lines [1,2]. Distinguishing the gear pair and turning pair with thick and thin lines is known as labeling of graphs. Otherwise the graph is known as an unlabeled graph [3]. There will be n (n-1) possible ways to add an additional vertex to each of the rotational isomorphic graph. For every one additional element added to a PGT of given number of links and one DOF, one gear pair and one turning pair will be added. Thus from a 3-link PGT, six 4-link PGTs are generated and from every 5-link PGT twenty 6-link PGTs are generated and so an. From the earlier published work [4,5] there will be 26 non-isomorphic 6-link rotational graphs and 80 non isomorphic 6-link displacement graphs are possible. Generation of PGTs from the No. of links is shown in Table 1.
Considering a 6-link PGT shown in Figure 1, it can be represented by a labeled graph as shown in Figure 2. A structural graph in Figure 2 is converted to rotational graph, by deleting the turning pair and marking the transfer vertex for each gear pair as shown in Figure 3 [2, 6].
A graph of a PGT can further be represented by a link to link adjacency matrix as per the following rules [2,3].
To test isomorphism in PGTS various researches used different methods like characteristics polyno-mial [7], converting unlabeled graphs into labeled graphs[2], minimum and maximum code method [8], Hamming

Table 1. Generation of pgts from no. of links.

Figure 1. Functional dlagram.

Figure 2. Structural graph.

Figure 3. Rotational graph.

number approach [1,9], Eigen vectors and Eigen values of adjacency matrix based method [10], genetic algorithm [11] and artificial neural network method [12], Canonical graph method [13] etc. Each method has its own advantages and disadvantages.
Hamming number method is used to check isomorphism in the PGTs and verify the structural aspects like parallelism, symmetry and compactness in PGTs [14].
In Hamming number method, from the adjacency matrix another matrix called Hamming matrix is defined as for the following rules [1,9]

Hamming matrix is also a symmetric matrix similar to adjacency matrix. For the 6 link PGT in Figure 2, the adjacency and hamming matrix are as given below.

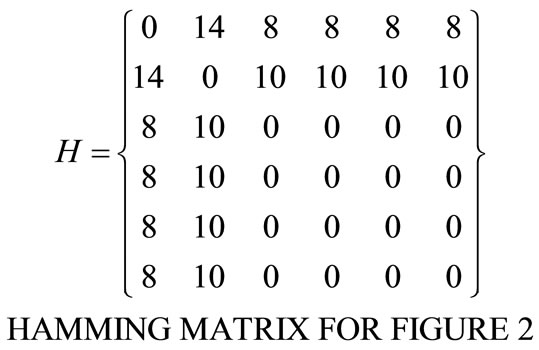
From the Hamming matrix, an invariant known as Hamming string 172 [54, 46, 18, 18, 18, 18] is written as per the definition of Hamming string [1,9] and this is used to detect isomorphism in PGTs. Also Hamming values of different elements in Hamming matrix of a PGT are also used to define symmetrical links [9] and symmetry in a given PGT [9].
In a PGT the position of a turning pair is identified by a level. If levels are assigned to a graph it is known as leveled graph [3]. A graph of a PGT with given number of links and one DOF, has number of Fundamental circuits and in a graph of PGT there is a vertex called Transfer vertex. The levels on one side of the transfer vertex must be same and different from the levels on the other side of Transfer vertex [1,2].
For a rotationally non-isomorphic graph, levels can be assigned to the turning pairs in different ways. Assigning levels to turning pair of 26 graphs of 6-link PGTs in as many ways as possible results in 80 non-isomorphic structural graphs [2].
For example for a 6-link PGT shown in Figure 1, Different Levels assigned to different turning pairs (12, 13, 14, 15 and 16) can be assigned in 5 different ways. They are as shown in Table 2.
Thus structural diagram for all the 26 non-isomorphic graphs can be drawn as per the labeling given in the Table 2 [3].
2. Generation of Seven Link PGTs
From the Twenty six, 6-link PGTs by adding one additional link (one turning pair and one gear pair) generated 7-links PGTS are 780. Out of these some PGTs are dis-
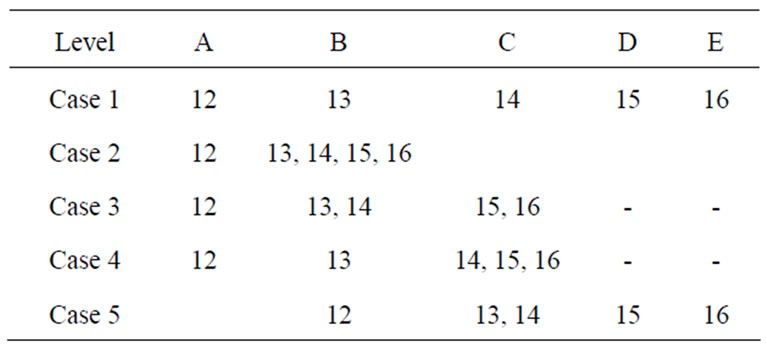
Table 2. No. of ways to assign different levels to the same structural graph.
carded due to violation of fundamental rule—9 [1,2]. Thus 213 PGTs are eliminated and remaining 567 PGTs are tested for structural isomorphism.
This resulted in 75 structurally isomorphic PGTs. Further verifying for rotational isomorphism, these 492 nonisomorphic structural graphs results in 159 non-isomorphic rotational graphs. While testing for isomorphism using Hamming number method it is observed that, PGTs with more symmetry resulted in less number of non isomorphic structural graphs and rotational graphs.
For the PGT shown in Figure 4, the Hamming matrix written from the adjacency matrix is given below. From the Hamming matrix, Hamming values of links (1, 2, 3, 4, 5, 6) are in order 216 [42, 42, 34, 34, 32, 32]. The PGT in Figure 4 is having three pairs of symmetry. Thus links 1&2 are symmetric about links 3, 4, 5 and 6. Links 3 & 4 are symmetric about links 1, 2, 5, 6. And finally links 5 & 6 are symmetric about links 1, 2, 3 and 4. Hence this PGT is having more symmetry.
3. Hamming and Adjacency Matrix
For the PGT in Figure 4, thirty, 7-link graphs are generated, out of which 11 are eliminated due to violation of rule F-9, and resulted in 11 non-isomorphic structural graphs and 7 non-isomorphic rotational graphs. Now consider another 6-link PGT as shown in Figure 5. It
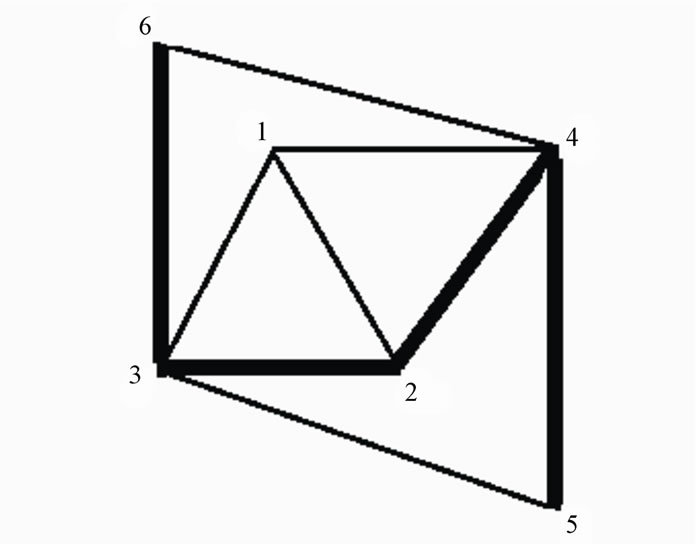
Figure 4. Six-link structural graph.
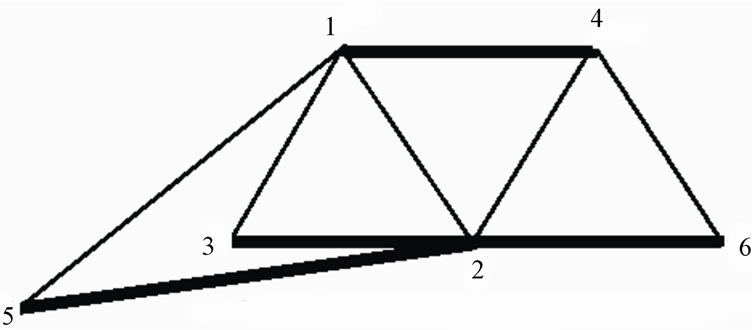
Figure 5. Six-link structural graph.
has two symmetric links 3 & 5 and is symmetric about links (1, 2, 4, & 6). This graph has resulted in 15 non-isomorphic structural graphs and 9 non-isomorphic rotational graphs.
Further consider a non-symmetrical graph shown in Figures 6 and 7. For PGT in Figure 6, which has no symmetry resulted in 25 non-isomorphic structural graphs and 11 non-isomorphic rotational graphs, And PGT in Figure 7 resulted in 23 non-isomorphic structural graphs and 13 non-isomorphic rotational graphs.
Thus symmetry in the PGTs resulted in less number of non-isomorphic rotational graphs for PGTs. However it has been observed that symmetry in a graph results in more number of levels compared to non-symmetric graphs.
4. Conclusions
Checking for isomorphism in PGTs is an important stage in structural synthesis of planetary gear trains. However
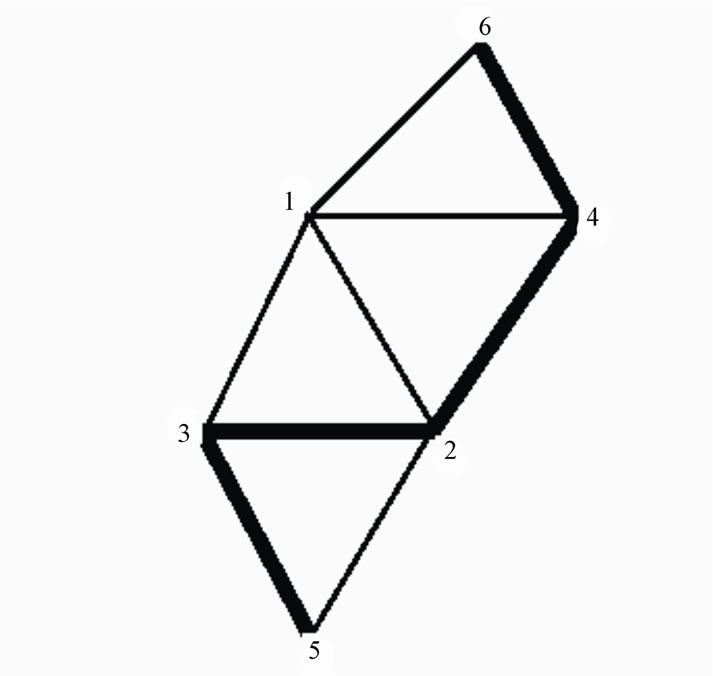
Figure 6. Six-link structural graph.
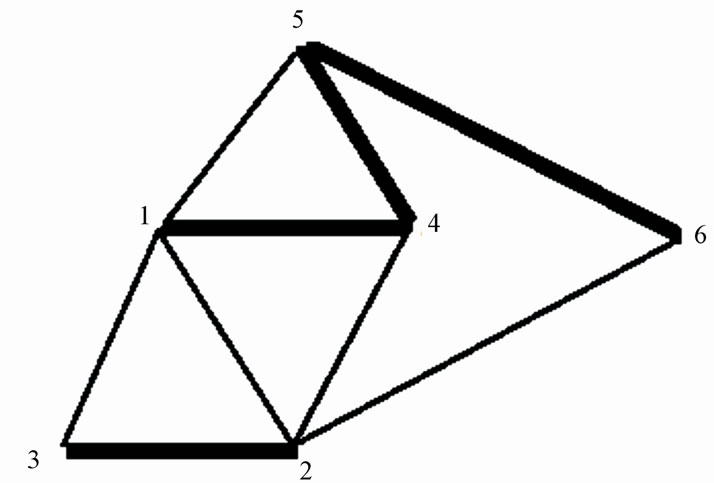
Figure 7. Six-link structural graph.
structural aspect like symmetry has an influence in the generation of PGTs. Higher the symmetry less in the number of non isomorphic graphs generated. However, the number of levels for a given graph of a PGT increases with symmetry in the graph.
5. REFERENCES
- I. Rajasri, Y. Rao and A. Gupta, “Structural Aspects of Symmetry and Its Effects on Generation of Planetary Gear Trains,” 2011 International Conference on Mechanical and Aerospace Engineering, New Delhi, 21-23 March 2011, pp. 530-533.
- L. W. Tsai, “An Application of the Linkage Characteristic Polynomial to the Topological Synthesis of Epicyclic Gear Trains,” ASME Journal of Mechanisms, Transactions and Automation in Design, Vol. 199, No. 3, 1987, pp. 329-336. doi:10.1115/1.3258798
- R. R.Shankar and T. S. Mruthyunjaya, “Computerized Synthesis of the Structure of General Kinematic Chains,” Mechanism and Machine Theory, Vol. 20, No. 5, 1985, pp. 367-387. doi:10.1016/0094-114X(85)90042-4
- F. Buchsbaum and F. Freudenstein, “Synthesis of Kinematic Structure of Geared Kinematic Chains and Other Mechanisms,” Journal of Mechanisms, Vol. 5, 1970, pp. 357-392. doi:10.1016/0022-2569(70)90068-6
- F. Freudenstein, “An Application of Boolean Algebra to the Motion of Epicyclic Drives,” ASME Journal of Engineering for Industry, Vol. 93, Series-B, 1971, pp. 176- 182
- Z. Levai, “Structure and Analysis of Planetary Gear Trains,” Journal of Mechanisms, Vol. 3, No. 3, 1968, pp. 131-148. doi:10.1016/0022-2569(68)90352-2
- G. Chatterjee and L.-W. Tsai, “Enumeration of Epicyclic Type Automatic Transmission Gear Trains,” Technical Report, ISR, 1995.
- A. G. Ambekar and V. P. Agrawal, “Canonical Numbering of Kinematic Chains and Isomorphism Problem,” Mechanism and Machine Theory, Vol. 22, No. 5, 1987, pp. 453-461. doi:10.1016/0094-114X(87)90062-0
- A. C. Rao and Y. Rao, “Symmetry in Planetary Gear Trains,” Indian Journal of Engineering & Material Sciences, Vol. 9, October 2002, pp. 311-314.
- Z. Y. Chang, C. Zhang, Y. H. Yang, et al., “A New Method to Mechanism Kinematic Chain Isomorphism Identification,” Mechanism and Machine Theory, Vol. 37, No. 4, 2002, pp. 411-417. doi:10.1016/S0094-114X(01)00084-2
- A. C. Rao, “Genetic Algorithm for Topological Characteristics of Kinematic Chains,” Journal of Mechanical Design, Vol. 122, No. 2, 2000, pp. 228-231. doi:10.1115/1.533569
- F. G. Kong, Q. Li and W. J. Zhang, “An Artificial Neural Network Approach to Mechanism Kinematic Chain Isomorphism Identification,” Mechanism and Machine Theory, Vol. 34, No. 2, 1999, pp. 271-283. doi:10.1016/S0094-114X(98)00035-4
- H. S. Yan and A. S. Hall, “Linkage Characteristic Polynomials: Assembly, Theorems, Uniqueness,” Journal of Mechanical Design, Vol. 104, No. 1, 1982, pp. 11-20. doi:10.1115/1.3256301
- A Srinath. “Improved Synthesis of Planetary Gear Trains,” IE (I) Journal-MC, Vol. 86, October 2005, pp. 172-174.

