Engineering
Vol. 3 No. 4 (2011) , Article ID: 4596 , 4 pages DOI:10.4236/eng.2011.34041
Modeling of Slab Induction Heating in Hot Rolling by FEM
1Northeastern University at Qinhuangdao Branch, Northeastern University, Qinhuangdao, China
2State Key Laboratory of Rolling and Automation, Northeastern University, Shenyang, China
3Technical Center, Wuhan Iron and Steel Company, Wuhan, China
E-mail: meirbbaol@126.com
Received January 21, 2011; revised March 8, 2011; accepted March 21, 2011
Keywords: FEM, Induction heating, Heat generating rate model, Hot rolling, Temperature
ABSTRACT
FEM (Finite Element Method) has been widely used to solve temperature in hot rolling. The heat generating rate of electromagnetic field has been discussed in order to improve the efficiency and accuracy in the solution of induction heating. A new heat generating rate model was proposed and derived from the calculated results by FEM software in consideration of work frequency, source current density, and the air gap between induction coil and slab. The calculated distribution of heat generating rate in the skin depth by the model is satisfying and reliable compared with that of FEM software. Then, the mathematic model of the heat generating rate model is considered as the density of heat reservoir to solve the temperature in induction heating. Moreover, the temperature evolution of slab in induction heating from a hot rolling plant has been solved by the developed FE code and the calculated temperature has a good agreement with the measured value. Therefore, the heat generating rate model is suitable and efficiency to solve the temperature in induction heating by FEM.
1. Introduction
Induction heating is widely used in vehicle manufacture, cast-rolling, forging, preheating before rolling, heat treatment, galvanizing and so on. Compared to other heating technologies, induction heating has the advantages of high efficiency, fast heating rate, easy control etc. The mathematical model and FEM were used to analyze the induction heating by many researchers. A mathematical model and special simulation program were developed for the induction hardening process of axially symmetric workpiece [1]. The optimal control approach of induction heating was studied and the corresponding mathematical model was established by Olivier [2] and Favennec [3]. On the basis of Maxwell equations, a mathematical model was established to determine the coupled field during the high frequency induction heating [4]. The expression of magnetic permeability with temperature was derived from measured data and the induction heating was analyzed using 3D FEM by Hiroki [5]. With the development of iron and steel technologies, the induction heating has been used to heat strip quickly or uniformly in hot rolling process. Nicholas V. Ross [6] analyzed the different solenoidal and transverse flux heating methods for strip heating and discussed its application to the galvanizing and strip preheating according to experiments data. The references [7] used the FEM software to investigate the slab temperature distribution of induction heating in hot strip rolling.
It is difficult to predicting temperature accuracy because of multiple nonlinear relationships among induction heating parameters. Furthermore, the material electromagnetic and thermal physic properties are influenced by the temperature. In the case of the electromagnetic-thermal analysis by FEM, the heat generating rate obtained in the solution of electromagnetic field according to the Maxwell equations and then it is considered as the density of heat reservoir into the thermal analysis [8]. In the past, both electromagnetic and thermal field need to be obtained to solve the temperature in induction heating process and these methods reduce the solution efficiency and make the solution of temperature difficult in induction heating. In fact, the temperature can be solved through thermal analysis only on the premise of the density of heat reservoir obtained.
In the work, the max value of heat generating rate with different work frequency, source current density and air gap has been investigated on the basis of electromagnetic analysis by FEM software. Furthermore, the heat generating rate distribution with different element has been discussed according to the distance to edge. A new heat generating rate model has been discussed and set up successfully on the premise of taking the main factors into consideration. Then, the new model was used as the density of heat reservoir and embedded into the developed FE code for the thermal analysis in induction heating.
2. Finite Elements Model
2.1. Electromagnetic Analysis
The solution of electromagnetic field problem should be satisfied with Maxwell differential equations [8].
 (1)
(1)
where  is Laplacian,
is Laplacian,  the electric field (V/m),
the electric field (V/m), 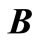 the magnetic induction intensity (T),
the magnetic induction intensity (T), 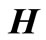 the magnetic intensity (A/m),
the magnetic intensity (A/m), 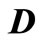 the electric displacement vector (C/m2),
the electric displacement vector (C/m2), 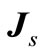 the source current vector,
the source current vector, 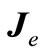 the induction current vector, and
the induction current vector, and 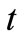 is time.
is time.
Additional equation can be described as
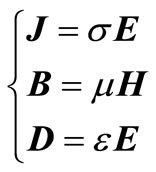 (2)
(2)
where ![]() is conductivity,
is conductivity, 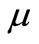 the magnetic inductivity, and
the magnetic inductivity, and ![]() is the dielectric constant,
is the dielectric constant, 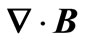 equals to zero, then the vector potential
equals to zero, then the vector potential  and
and 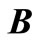 are expressed as follows
are expressed as follows
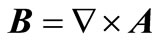 (3)
(3)
Substituting equation (3) into Maxwell equations then the finite element method solution of alternating magnetic field can be expressed as [9]:
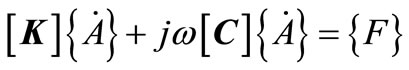 (4)
(4)
where 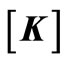 is coefficient matrices,
is coefficient matrices,  the magnetic damping matrices,
the magnetic damping matrices, ![]() the angular frequency,
the angular frequency, 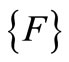 loadsand
loadsand 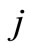 equals to
equals to .
.
2.2. Thermal Analysis
In the thermal analysis, variable 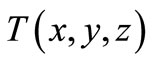 of transient temperature fields should be met with differential equation on 3D thermal conductivity [10].
of transient temperature fields should be met with differential equation on 3D thermal conductivity [10].
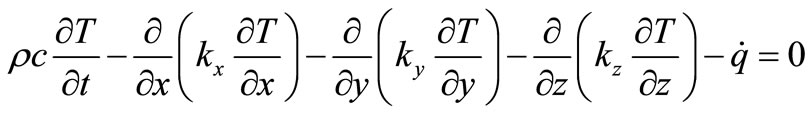 (5)
(5)
where ![]() is transient temperature of infinitesimal body (K),
is transient temperature of infinitesimal body (K),![]() the material density (kg/m3),
the material density (kg/m3), ![]() the material specific heat J/(kg·K),
the material specific heat J/(kg·K), 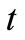 the time (s),
the time (s), 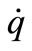 the density of heat reservoir (W/kg), and
the density of heat reservoir (W/kg), and  are material conductivity along
are material conductivity along 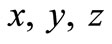 respectively.
respectively.
According to variation principle of thermal conductivity, temperature can be obtained when the temperature derivative of functional equals to zero
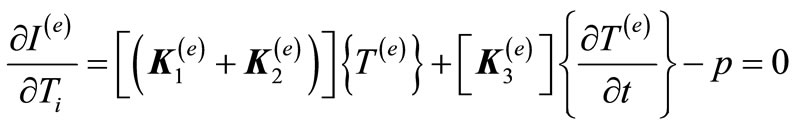 (6)
(6)
Element stiffness matrixes are assembled to integral stiffness matrix according to the Equation (6) and the partial differential equation can be expressed as
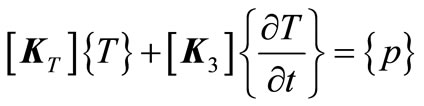 (7)
(7)
where 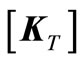 is temperature stiffness matrix, and
is temperature stiffness matrix, and 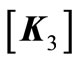 is variable temperature matrix.
is variable temperature matrix.
2.3. Electromagnetic-Thermal Coupled Process
It is complex for the analysis of induction heating process and the solution procedure of electromagnetic-thermal field with FEM is shown in Figure 1.
In the case of the electromagnetic-thermal analysis by FEM, the heat generating rate is considered as the density of heat reservoir in equation (8). In the FEM software, the heat generating rate is described as function of resistivity, and current density
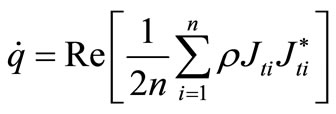 (8)
(8)
where Re denotes real component, 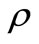 is resistivity,
is resistivity, 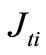 is current density in element,
is current density in element, 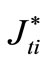 are conjugate values of current density.
are conjugate values of current density.
Equation (8) is obtained by electromagnetic field and it is inconvenient to obtain the current density in element. The lay out of induction heating is shown in Figure 2. L and H are length and thickness of workpiece, respectively. In the induction heating, the induction current and electromagnetic field are generated in the workpiece with
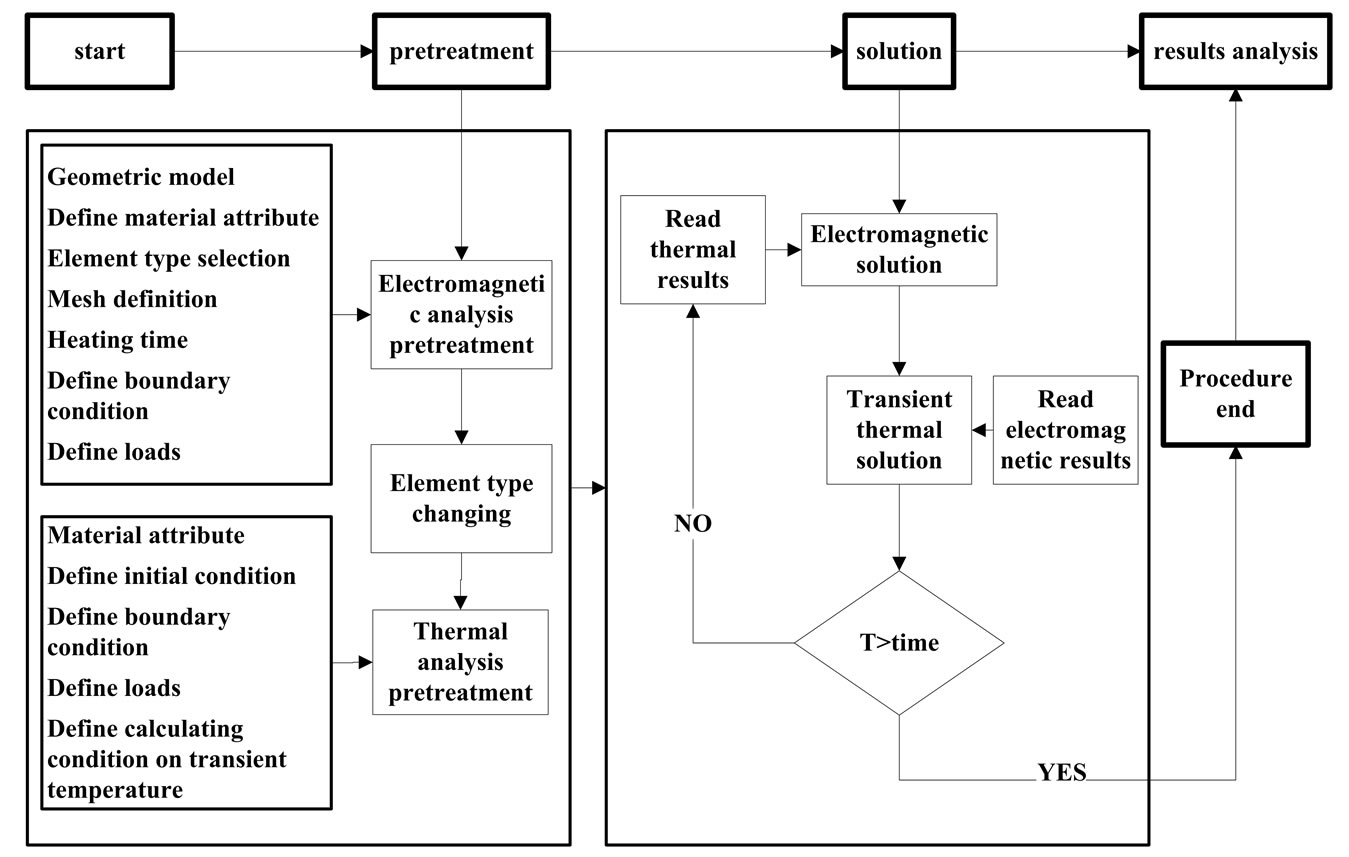
Figure 1. Solution procedure of Electromagnetic-thermal field.
the change of source current in the induction coil. Moreover, work frequency and air gap have important influence on the depth of induction current and induction heating [7]. Generally, low-frequency induction heating heat slab steel uniformly to improve microstructure during deforming process but high-frequency induction heating technologies usually apply to hot surface treatment mainly. For electromagnetic field, the induction current become weaken with the increase of distance between coil and workpiece. In addition, the heat generating rate of every element changes greatly at different position and the max value lies in the surface of workpiece [7]. Therefore, the mainly influent factors including work frequency, current density, air gap and distance of one element to edge were taken into account and a new heat generating rate model is investigated in the work and the new model is written in
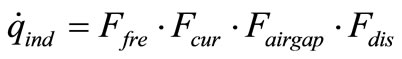 (9)
(9)
where 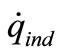 is heat generate of electromagnetic field in induction heating,
is heat generate of electromagnetic field in induction heating, 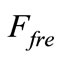 the function of work frequency,
the function of work frequency,  the function of source current density,
the function of source current density,  the function of air gap, and
the function of air gap, and 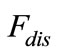 is the function of distance of one element to edge.
is the function of distance of one element to edge.
3. Modeling of Heat Generating Rate
3.1. Heat Generating Rate on Surface
The maximum of heat generating rate on the slab surface is the highest because of skin effect. In addition, the maximum of heat generating rate and distance of element in the skin depth have important influence on the distribution of heat generating rate. Therefore, in the solution procedure, the electromagnetic field is discussed by FEM and the heat generating rate model of every element is derived from the calculated results. In the analysis of induction heating, the source current density is more than 105 A/m2 and the air gap is less than 0.15 m according to the requirements in production.
Figure 3 shows the influence of work frequency, air gap and source current density on the change of heat generating rate on surface of slab in induction heating. It is found that the heat generating rate increase linearly with the increase of the work frequency (Figure 3(a)). In order to set up model, the value with 1000 Hz is considered as the bases to calculate the other values with different work frequency. Then, the function of work frequency is expressed as
 (10)
(10)
where 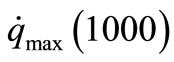 is heat generating rate on surface with 1000 Hz.
is heat generating rate on surface with 1000 Hz.
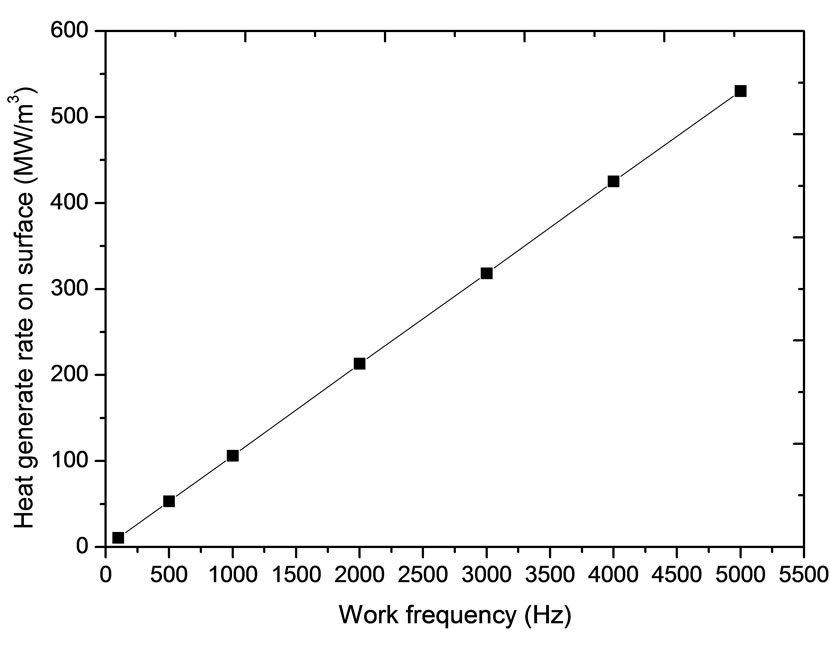
With the increase of air gap, the electromagnetic field will be weakened and the different air gap from 0.001 m to 0.15 m has been discussed (Figure 3(b)). It can be seen that the heat generating rate on surface decreases linearly with the increase of air gap. The maximum values of heat generating rate based on the 0.01 m can be described as the value with 0.01 m and 1000 Hz is considered as the bases to calculate the other values with different air gap and the function of work frequency is

Figure 2. Lay out of induction heating.
described as
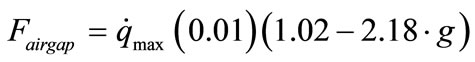 (11)
(11)
where  is heat generating rate on surface with 0.01 m, and
is heat generating rate on surface with 0.01 m, and ![]() is less than 0.15 m.
is less than 0.15 m.
The change of eddy current density value on the surface with different is shown in Figure 3. It can be seen that the relationship between heats generate rate on surface and source current density is parabola (Figure 3(c)). The heat generating rate on the surface of slab with 1000 Hz, 0.01 m and different source current density is described as the follow function
 (12)
(12)
where 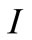 is source current density and its value is more than 105.
is source current density and its value is more than 105.
3.2. Distribution of Heat Generating Rate
In the case of solution of thermal analysis by the FEM, the heat generating rate of every element in the skin depth should be given. Therefore, the heat generating rate of element at any position in the slab should be obtained. During solving the electromagnetic process by the boundary element method (BEM), the distribution of the induced eddy current density per depth 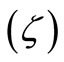 is determined approximately by the equation (13) by Cajner [1]:
is determined approximately by the equation (13) by Cajner [1]:
 (13)
(13)
where 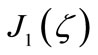 is distribution of eddy current (A/m2),
is distribution of eddy current (A/m2), 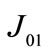 a fixed value in a direction (A/m2),
a fixed value in a direction (A/m2),  the complex vector,
the complex vector, 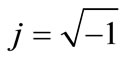 ,
, ![]() the circular frequency (rad/s),
the circular frequency (rad/s),  the magnetic permeability (H/m), and
the magnetic permeability (H/m), and  is electric conductivity (S/m).
is electric conductivity (S/m).
It is found that the relationship between the distribution of eddy current density and depth of the boundary element is exponential. In the paper, the distribution of heat generating rate with different work frequency from 100 Hz to 1 MHz has been discussed. The distribution of heat generating rate from center to surface with 100 Hz and 50 kHz is shown in Figure 4. It can be seen the distribution of heat generating rate is exponential. With the increase of the frequency the skin depth is less and the skin effect is more obvious.
Through investigating the data the heat generating rate distribution is described as
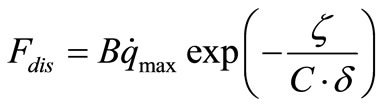 (14)
(14)
where ![]() is skin depth (m),
is skin depth (m), 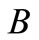 and
and 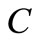 are constants,
are constants,  the heat generating rate on surface with 0.01 m air gap and 1000 Hz work frequency,
the heat generating rate on surface with 0.01 m air gap and 1000 Hz work frequency, ![]() the distance of every element in the skin depth, and
the distance of every element in the skin depth, and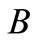 ,
, 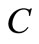 are constants, which are related to the slab size and FE mesh.
are constants, which are related to the slab size and FE mesh.
According to the function of work frequency, source current density, air gap and distance to edge of element, the total heat generating rate model can be expressed as:
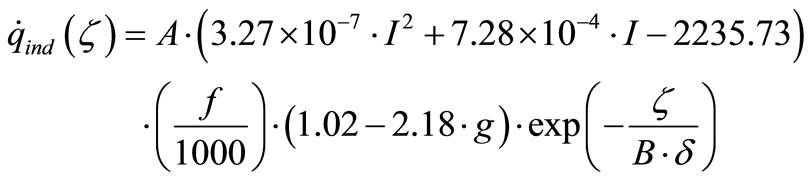 (15)
(15)
where  is heat generating rate of induction heating (W/m3),
is heat generating rate of induction heating (W/m3),  the source current density (A/m2),
the source current density (A/m2),  the work frequency (Hz),
the work frequency (Hz),  the air gap (m),
the air gap (m), ![]() the distance of element to surface in skin depth (m),
the distance of element to surface in skin depth (m), ![]() the skin depth (m), and
the skin depth (m), and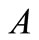 ,
, 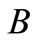 are constants.
are constants.
4. Model Test
4.1. Comparison of Heat Generating Rate
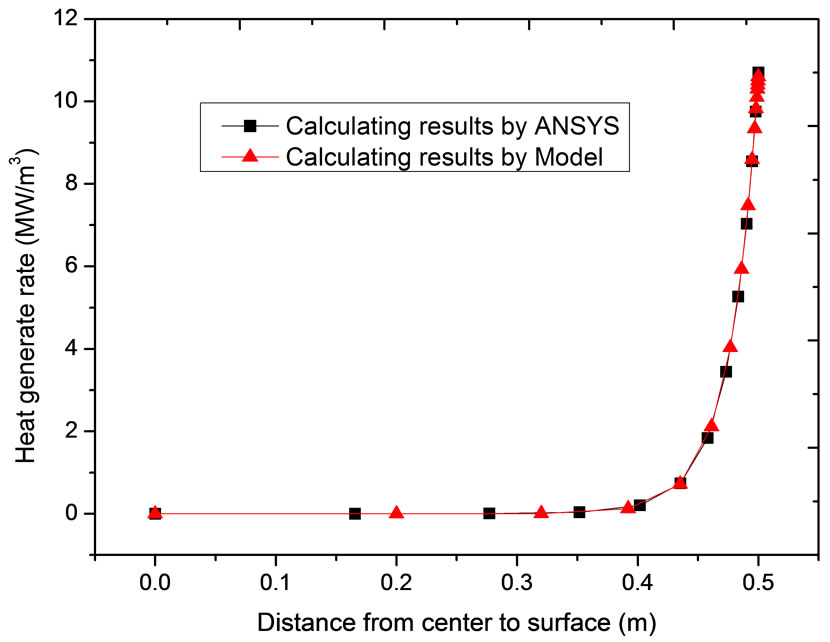
The comparison of heat generating rate by ANSYS and the model can be seen in Figure 5. It can be seen that the heat generating rate distribution by the model have a good agreement with the calculated results by solution of electromagnetic field with ANSYS. The model is reliable for predicting heat generating rate of the electromagnetic field.
4.2. Comparison of Temperature
In order to verify the validation of the new model, the FE code has been developed by FORTRAN. Then the model
 (a)
(a)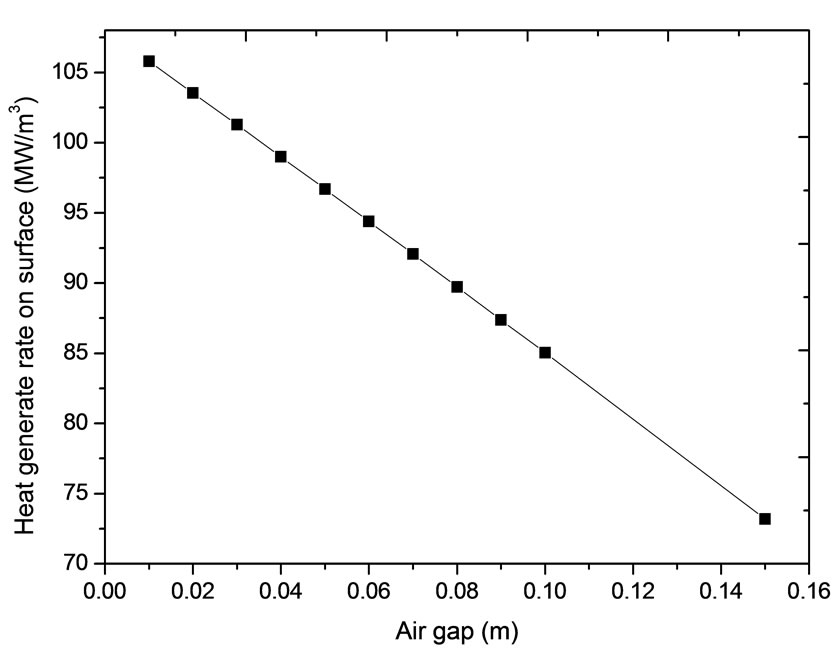 (b)
(b) (c)
(c)
Figure 3. Change of heat generating rate on surface with different parameters, (a) Influence of work frequency (b) influence of air gap (c) Influence of source current density.
 (a)
(a)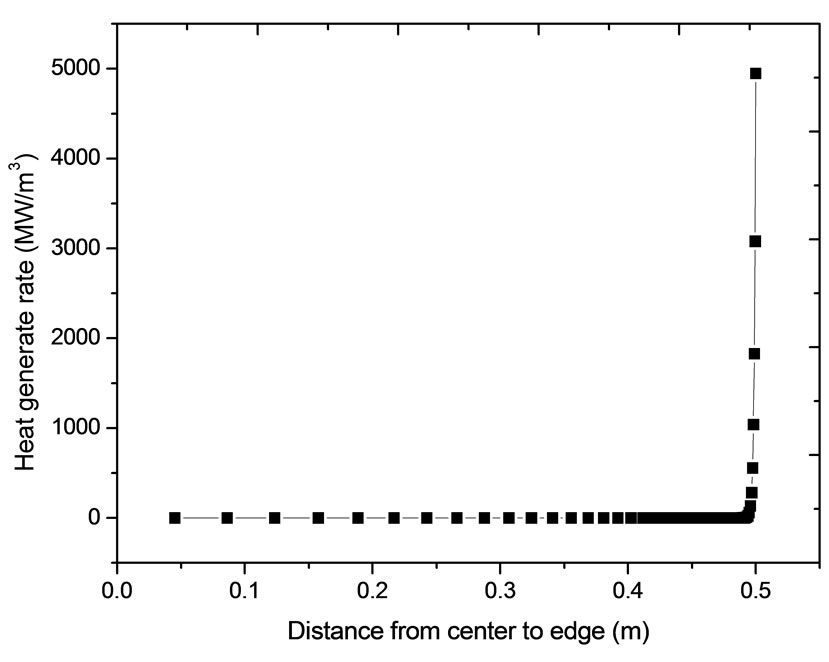 (b)
(b)
Figure 4. Distribution of heat generating rate. (a) 100 Hz, (b) 50 kHz.
was embedded into the FE code as the density of heat reservoir to solve temperature in induction heating under the same experimental conditions. The calculating conditions are described as follows: physical model is 11.0 × 1.0 × 0.2 m3, initial temperature is 850˚C, heating time is 30 min, frequency is 110 Hz, source current density is 1.3 × 107 (A/m2),  equals to 1,
equals to 1, 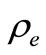 is 1.24 × 10−6 (Ω·m),
is 1.24 × 10−6 (Ω·m),  is 4π × 10−7 (T/A),
is 4π × 10−7 (T/A),  is 28 (W/(m·K)), Specific heat
is 28 (W/(m·K)), Specific heat ![]() is 670 (J/(Kg·K)),
is 670 (J/(Kg·K)),  is 7800 (kg/m3),
is 7800 (kg/m3), ![]() is 0.6 and
is 0.6 and ![]() is 5.67 × 10−8 W/(m2·K4),
is 5.67 × 10−8 W/(m2·K4), 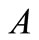 and
and 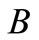 are set to 0.3 and 0.95.
are set to 0.3 and 0.95.
It can be seen that the calculated temperature had a good agreement with the measured results and the new model is suitable for solution to temperature in induction heating (Figure 6). Additionally, in the initial time, the temperature is changed slowly because of the heat loss of radiation and the insulating material has important influ-
 (a)
(a)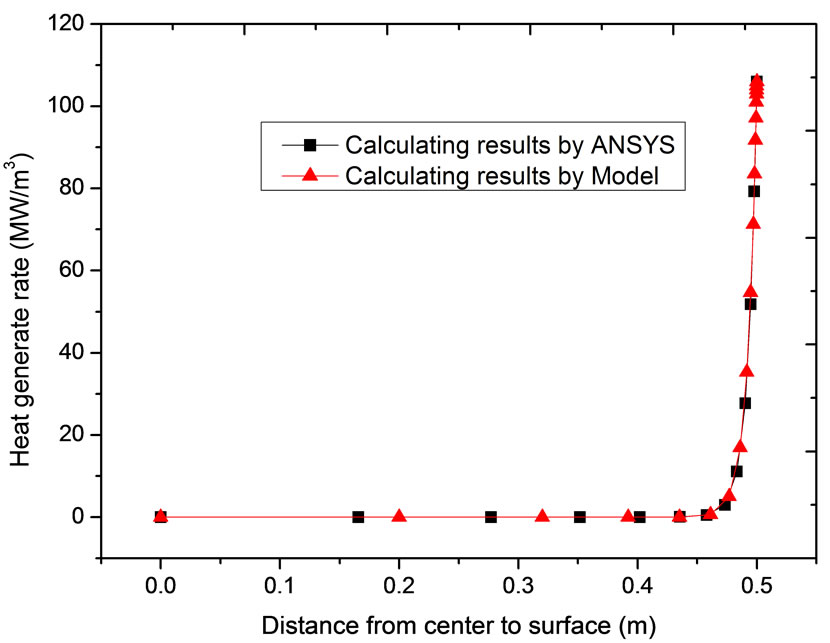 (b)
(b)
Figure 5. Comparison of heat generating rate, (a) f = 100 Hz, I = 1.8 × 107 A/m2, g = 0.01 m; (b) f = 1000 Hz, I = 1.8 × 107A/m2, g = 0.01 m.

Figure 6. Comparison of temperature on surface of slab.
ence on the induction heating. Then, the temperature changes fast at first and then slowly with the increase of time in the solution of induction heating.
5. Conclusions
The heat generating rate of electromagnetic field was investigated by the FEM and the heat generating rate model derived from the calculated results. The model was considered as density of heat reservoir into the thermal analysis. The influence of work frequency, source current density, air gap and distance of every element to surface on the heat generating rate has been discussed. With the increase of work frequency and air gap the heat generating rate on surface increase linearly. However, its value is increased greatly with different source current density and the relationship is parabola type. Furthermore, the distribution of heat generating rate is exponential with the distance of every element from centre to surface in the skin depth. The temperature distribution in induction heating from a certain plant was solved according to the new model. The calculated results have a good agreement with the measured values and the new model is suitable for solution to tempe-rature in induction heating.
6. Acknowledgment
The authors would like to acknowledge National Natural Science Foundation Project (No. 50534020) and Qinhuangdao Technology Support Project (No. 201001A006) for the financial support.
7. REFERENCES
- F. Cajner, B. Smoljan and D. Landek, “Computer Simulation of Induction Hardening,” Journal of Materials Processing Technology, Vol. 157-158, 20 December 2004, pp. 55-60. doi:10.1016/j.jmatprotec.2004.09.017
- O. Bodart, A.-V. Boureau and R. Touzani, “Numerical Investigation of Optimal Control of Induction Heating Processes,” Applied Mathematical Modelling, Vol. 25, No. 8, August 2001, pp. 697-712. doi:10.1016/S0307-904X(01)00007-5
- Y. Favennec, V. Labb and F. Bay, “Induction Heating Processes Optimization a General Optimal Control Approach,” Journal of Computational Physics, Vol. 187, No. 1, 2003, pp. 68-94. doi:10.1016/S0021-9991(03)00081-0
- H. Shen, Z. Q. Yao, Y. J. Shi and J. Hu, “Study on Temperature Field Induced in High Frequency Induction Heating,” Acta Metallurgica Sinica (English Letters), Vol. 19, No. 3, 2006, pp. 190-196. doi:10.1016/S1006-7191(06)60043-4
- H. Kawaguchi, M. Enokizono and T. Todaka, “Thermal and Magnetic Field Analysis of Induction Heating Problems,” Journal of Materials Processing Technology, Vol. 161, No.1-2, 2005, pp. 193-198. doi:10.1016/j.jmatprotec.2004.07.075
- N. V. Ross and G. J. Jackson, “Induction Heating of Strip Solenoidal and Transverse Flux,” Iron and Steel Engineer, Vol. 68, No. 6, June 1992, pp. 39-43.
- R. B. Mei, C. S. Li, B. Han and X. H. Liu, “FEM Analysis of Slab Induction Heating,” Iron and Steel, Vol. 43, No. 2, 2008, pp. 56-60.
- D.-C. Ko, G.-S. Min, B.-M. Kim and J.-C. Choi, “Finite Element Analysis for the Semi-Solid State Forming of Aluminium Alloy Considering Induction Heating,” Journal of Materials Processing Technology, Vol. 100, No. 1-3, 2000, pp. 95-104. doi:10.1016/S0924-0136(99)00459-8
- G. B. Zhang, Y. H. Wang and X. X. Dong, “The Finite Element Simulation of Continuous Casting of Square Billet during the Induction Heating,” Journal of He-bei Institute of Technology, Vol. 27, No. 4, 2005, pp. 24-30.
- X. H. Liu, “Rigid Plastic FEM and Its Application in Rolling,” Metallurgy Industry Press, Beijing, 1994, pp. 300-324.

