Engineering
Vol. 3 No. 1 (2011) , Article ID: 3725 , 4 pages DOI:10.4236/eng.2011.31007
Regression Models of the Impact of Rockmass and Blast Design Variations on the Effectiveness of Iron Ore Surface Blasting
Department of Chemical & Mining Engineering, College of Engineering & Technology,
University of Dar es Salaam, Dar es Salaam, Tanzania
E-mail: massaweantipas@hotmail.com
Received October 2, 2010; revised November 23, 2010; accepted November 26, 2010
Keywords: Blasting Effectiveness, Oversize generation, Blasthole Productivity, Blasting Cost, Rockmass Parameters, Blast Design Parameters, Regression Models
ABSTRACT
The desired economics of hard rock surface mining is mainly determined by the para-meters of process design which minimize the overall cost per tonne of the rock mined in drilling, blasting, handling and primary crushing in given rockmass conditions. The most effective parameters of process design could be established based on the regression models of the cumulative influence of rockmass and mine design parameters on the overall cost per tonne of the rock drilled, blasted, handled and crushed. These models could be developed from the huge data accumulated worldwide on the costs per tonne of hard rock surface mining in drilling, blasting, handling and primary crushing vs the parameters of rockmass and mine design. This paper only dwelt on the development of regression models for oversize generation, blasthole productivity and blasting cost for iron ore surface mines, whose data is available. The SPSS standard statistical correlation – regression analysis software was used in the analysis. Interpretation of the models generated shows that the individual effects of the determinant rockmass and blast design parameters on oversize generation, blasthole productivity and blasting cost are all in compliance with the findings of other researchers and the theory of explosive rock fragmentation and could be used for the estimation of oversize generation, blasthole productivity and blasting cost in rockmass and blast design conditions similar to those of the iron ore surface mines examined in this study. However, the regression models obtained here could not be used alone for the optimization of blast design because most of the determinant parameters also have conflicting effect on the other processes of drilling, handling and primary crushing the blasted rock. Also, the quality and content of the regression models could be enhanced further by increasing the content of rockmass and blast design parameters and the volume of data considered in the regression analysis.
1. Introduction
Oversize generation, blasthole productivity and cost per tonne of rock blasted are the three main indices of hard rock surface blasting effectiveness and are dependent on rockmass and blast design parameters. The determinant parameters differ from one mine to the other and some of the blast design parameters could be regulated to deliver the desired blasting effectiveness. The individual influence of the determinant parameters on blasting effectiveness has been studied by several authors [1-13], but their cumulative influence on the same is yet to be formulated. However, the huge statistical data generated from the well organized and documented large scale hard rock surface mines operating in variable conditions worldwide constitutes the only readily available resource which could be used for the analysis and generation of the regression models of oversize generation, blasthole productivity and cost per tonne of the rock blasted fit on rockmass and blast design parameters. For example, the statistical data available on several large scale iron ore surface mines which operated in the former Soviet Union could be used to develop regression models of iron ore surface blasting effectiveness. Therefore, aim in this paper is to develop the regression models of oversize generation, blasthole productivity and cost per tonne of the rock blasted fit on rockmass and blast design parameters of iron ore surface blasting, based on the blasting data published for the year 1970 for 10 large scale iron ore surface mines which operated in the former Soviet Union [6].
2. Indices of Blasting Effectiveness
2.1. Oversize Generation
Oversize generation is a quality index of blasting effectiveness, characterizing the percentage of the blasted rock product  which requires secondary blasting before it could be allowed into the downstream processes of handling and primary crushing. Blast design parameters which are not compatible with the rockmass conditions of blasting constitute the main cause of excessive oversize generation. Excessive oversize generation means extra cost on conducting the inefficient secondary blasting. The desired economics of hard rock surface mining could be achieved from the parameters of blast design delivering the minimum oversize and overall cost per tonne in drilling, blasting, handling and primary crushing in given rockmass conditions [1,7,8,10-12].
which requires secondary blasting before it could be allowed into the downstream processes of handling and primary crushing. Blast design parameters which are not compatible with the rockmass conditions of blasting constitute the main cause of excessive oversize generation. Excessive oversize generation means extra cost on conducting the inefficient secondary blasting. The desired economics of hard rock surface mining could be achieved from the parameters of blast design delivering the minimum oversize and overall cost per tonne in drilling, blasting, handling and primary crushing in given rockmass conditions [1,7,8,10-12].
2.2. Blasthole Productivity
Blasthole productivity  is a quantity index of blasting effectiveness, characterizing the volume of rock blasted per unit of blasthole length. The maximum blasthole productivity achievable from hard rock surface blasting is calculated according to the formula shown on (1) [1,7,9-11]:
is a quantity index of blasting effectiveness, characterizing the volume of rock blasted per unit of blasthole length. The maximum blasthole productivity achievable from hard rock surface blasting is calculated according to the formula shown on (1) [1,7,9-11]:
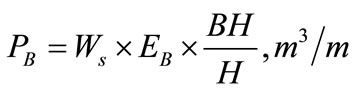 (1)
(1)
Where: 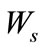 - burden at bench toe
- burden at bench toe ;
; 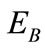 - blasthole spacing
- blasthole spacing ;
; 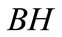 - bench height
- bench height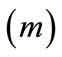 ;
;  - blashole length
- blashole length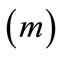 .
.
Blasthole productivity could increase as a result of the increase of . The increase of
. The increase of 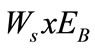 could also cause the increase of oversize generation and the cost on secondary blasting but the total volume of drilling work
could also cause the increase of oversize generation and the cost on secondary blasting but the total volume of drilling work  decreases. The desired economics of hard rock surface mining could be achieved from the parameters of blast design which deliver the maximum blasthole productivity and the minimum overall cost per tonne in drilling, blasting, handling and primary crushing.
decreases. The desired economics of hard rock surface mining could be achieved from the parameters of blast design which deliver the maximum blasthole productivity and the minimum overall cost per tonne in drilling, blasting, handling and primary crushing.
2.3. Blasting Cost
Blasting cost  is the overall quality index of blasting effectiveness and one of the components of the overall cost per tonne of hard rock surface mining in drilling, blasting, handling and primary crushing. This index is characterizes the overall cost per tonne of the rock blasted in charging and firing and secondary blasting [1,10,11]. The desired economics of hard rock surface mining could be achieved from the blast design parameters delivering the established production capacity of the mine at the maximum blasthole productivity, minimum generation of oversize, minimum blasting and overall costs per tonne of the rock mined in drilling, blasting, handling and primary crushing.
is the overall quality index of blasting effectiveness and one of the components of the overall cost per tonne of hard rock surface mining in drilling, blasting, handling and primary crushing. This index is characterizes the overall cost per tonne of the rock blasted in charging and firing and secondary blasting [1,10,11]. The desired economics of hard rock surface mining could be achieved from the blast design parameters delivering the established production capacity of the mine at the maximum blasthole productivity, minimum generation of oversize, minimum blasting and overall costs per tonne of the rock mined in drilling, blasting, handling and primary crushing.
3. Regression Models of Blasting Effectiveness
3.1. Description
The levels of oversize generation, blasthole productivity and cost per tonne of the rock blasted are determined by the parameters of rockmass and blast design. Any of the rockmass and blast design parameters presented on Table 1 could influence on blasting effectiveness [1,3-6, 10-12]. The effects of blast design parameters on the costs per tonne of the rock blasted in drilling, blasting, handling and primary crushing are conflicting. Therefore, optimum blast design parameters should be the ones delivering the established production capacity of the mine at the minimum overall cost per tonne of the rock blasted in drilling, blasting, handling and primary crushing. Consequently, the assessment of blasting effectiveness and optimization of blast design should be based on the mathematical models of the cumulative influence of rockmass and blast design parameters on oversize generation, blasthole productivity and cost per tonne of the rock blasted. These models are one of the techno-economic models of processes in the mining industry, which are developed using the method of regression analysis [13]. However, the effectiveness of regression analysis depends on the availability of the necessary content and volume of data in respect of the costs per tonne of the rock blasted in drilling, blasting, handling and primary crushing vs the parameters of rock mass and blast design.
3.2. Development
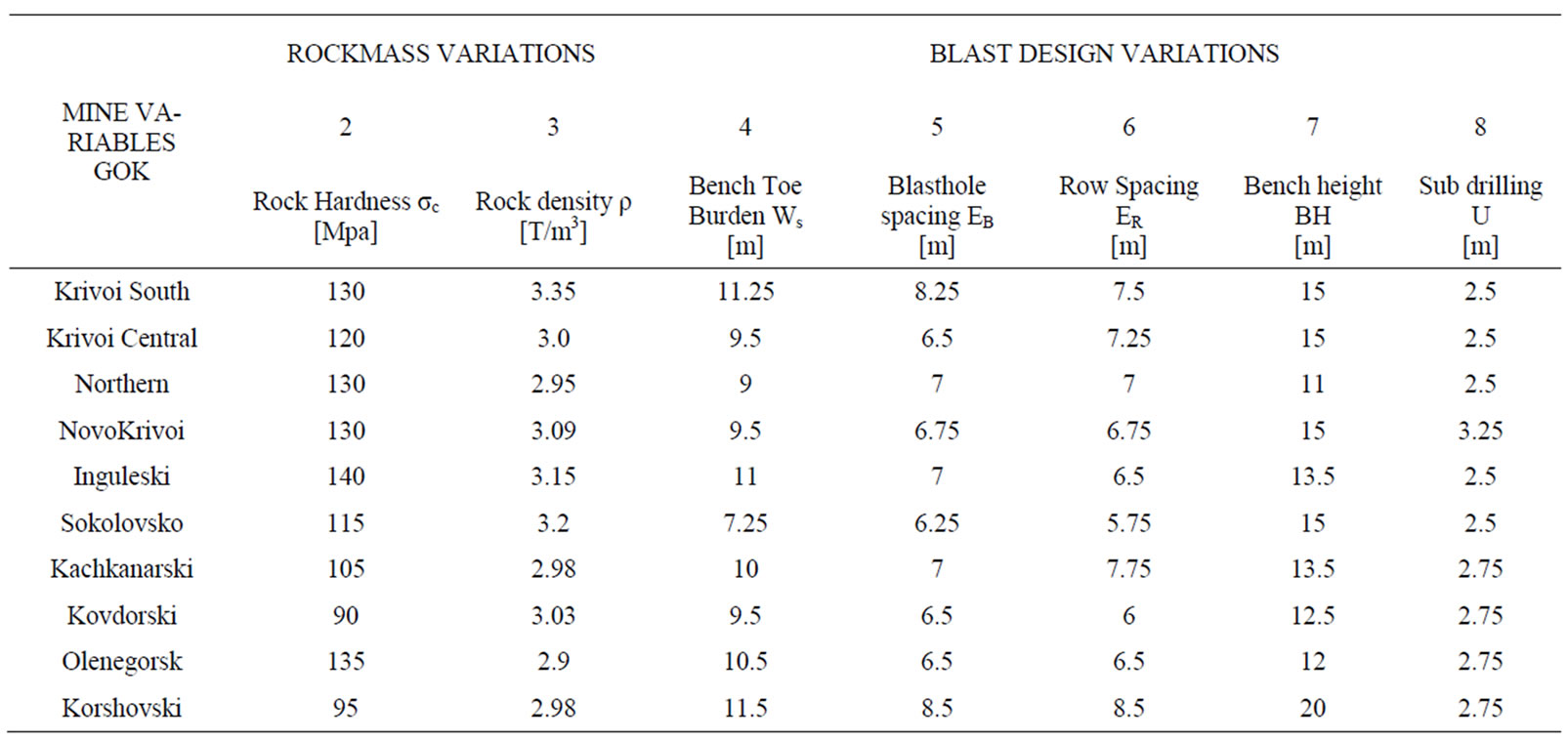
Regression models for the assessment of large scale iron ore surface blasting effectiveness were generated from the data available on the statistics of rockmass and blast

Table 1. Determinant parameters.
design parameters of 10 large scale iron ore surface mines in the former Soviet Union, whose average values for the year 1970 are shown on the appendix. The SPSS standard statistical correlation-regression analysis software was used to generate the regressions models of oversize generation , blasthole productivity
, blasthole productivity 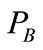 and blasting cost
and blasting cost 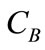 fit on the parameters of rockmass (hardness and density) and blast design (bench toe burden, blasthole spacing, rows spacing, bench height, subdrilling, stemming, powder factor, number of rows blasted, volume of rock blasted per blast and number of blasts per year). The models generated are shown on (2,3).
fit on the parameters of rockmass (hardness and density) and blast design (bench toe burden, blasthole spacing, rows spacing, bench height, subdrilling, stemming, powder factor, number of rows blasted, volume of rock blasted per blast and number of blasts per year). The models generated are shown on (2,3).
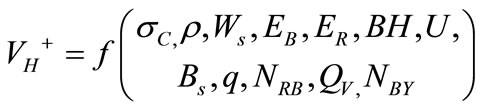 (2)
(2)
 (3)
(3)
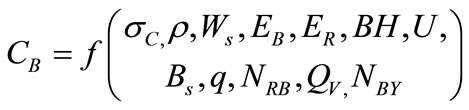 (4)
(4)
Important rockmass and blast design parameters such as, rock blastability, rock P-wave seismic velocity, type of explosive, blasthole diameter, charge diameter, detonation velocity, charge design; type of initiation system and delay interval (s), etc. were not considered in the regression analysis because they were almost the same for the 10 mines examined. Beside, their data were not available.
Model 1: Over size generation, %
The value of R2 is 0.884 showing that the five predictors entered in the regression analysis account for 88.4% of the variation in the percentage of oversize, while the F change is 6.093 and significant value is 0.052 slightly greater than 0.05 showing that the model is to a great extent significantly better at predicting the percentage of oversize generation than using the mean as the best guess. The following variables were found to be significant for the generation of oversize %: rock density, volume of rock blasted per blast, blasthole spacing and bench height. Compressive rock strength is the only variable found insignificant and was not shown on Table 2.
Explanation of variables and their coefficients
1) Rock density : This value indicates that as rock density increases by one unit, percentage of oversize increases by 10.704 units. This interpretation is true only if the effects of other variables in the model are held constant. The t-test
: This value indicates that as rock density increases by one unit, percentage of oversize increases by 10.704 units. This interpretation is true only if the effects of other variables in the model are held constant. The t-test  associated with this value indicates that it is significant
associated with this value indicates that it is significant . Rock density is making a significant contribution to the model.
. Rock density is making a significant contribution to the model.

Table 2. Significant variables and their coefficients.
2) Volume of rock blasted per blast : This value indicates that as volume of rock blasted in a round increases by one unit, percentage of oversize decreases by 0.012 units. This interpretation is true only if the effects of other variables in the model are held constant. The t-test
: This value indicates that as volume of rock blasted in a round increases by one unit, percentage of oversize decreases by 0.012 units. This interpretation is true only if the effects of other variables in the model are held constant. The t-test 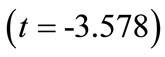 associated with this value indicates that it is significant
associated with this value indicates that it is significant . The volume of rock blasted per blast is making a significant contribution to the model.
. The volume of rock blasted per blast is making a significant contribution to the model.
3) Blasthole spacing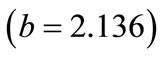 : This value indicates that as blasthole spacing increases by one unit, percentage oversize increases by 2.136 units. This interpretation is true only if the effects of other variables in the model are held constant. The t-test
: This value indicates that as blasthole spacing increases by one unit, percentage oversize increases by 2.136 units. This interpretation is true only if the effects of other variables in the model are held constant. The t-test 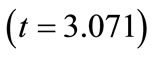 associated with this value indicates that it is significant
associated with this value indicates that it is significant . Blasthole spacing is making a significant contribution to the model.
. Blasthole spacing is making a significant contribution to the model.
4) Bench height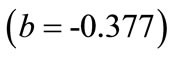 : This value indicates that as bench height increases by one unit, percentage oversize decreases by 0.377 units. This interpretation is true only if the effects of other variables in the model are held constant. The t-test
: This value indicates that as bench height increases by one unit, percentage oversize decreases by 0.377 units. This interpretation is true only if the effects of other variables in the model are held constant. The t-test 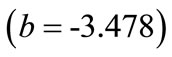 associated with this value indicates that it is significant (*p > .05). Bench height is making a significant contribution to the model.
associated with this value indicates that it is significant (*p > .05). Bench height is making a significant contribution to the model.
5) Compressive rock strength : This value indicates that as compressive rock strength increases by one unit, percentage of oversize increases by 0.245 units. This interpretation is true only if the effects of other variables in the model are held constant. The t-test
: This value indicates that as compressive rock strength increases by one unit, percentage of oversize increases by 0.245 units. This interpretation is true only if the effects of other variables in the model are held constant. The t-test  associated with this value indicates that it is not significant
associated with this value indicates that it is not significant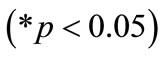 . The contribution of compressive rock strength to the model is not significant and therefore was removed.
. The contribution of compressive rock strength to the model is not significant and therefore was removed.
Model 2: Blasthole productivity, m3/m
The value of 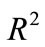 is 1.000 showing that the eight predictors entered in the regression analysis account for 100.00% of the variation in the blasthole productivity. The
is 1.000 showing that the eight predictors entered in the regression analysis account for 100.00% of the variation in the blasthole productivity. The  change is 1435.690 and is much greater than 1, showing that the model is significantly better at predicting blasthole productivity than using the mean as the best guess (significant
change is 1435.690 and is much greater than 1, showing that the model is significantly better at predicting blasthole productivity than using the mean as the best guess (significant ). The variables found to be significant for the blasthole productivity include: burden at bench toe, blasthole spacing, powder factor, rock hardness, subdrilling and stemming height. The other variables included in the analysis: rock density and volume of rock blasted were not found to be significant and were not shown in Table 3 of results.
). The variables found to be significant for the blasthole productivity include: burden at bench toe, blasthole spacing, powder factor, rock hardness, subdrilling and stemming height. The other variables included in the analysis: rock density and volume of rock blasted were not found to be significant and were not shown in Table 3 of results.
Explanation of variables and their coefficients
1) Burden at bench toe : This value indicates that as burden at bench toe increases by one unit, blasthole productivity increases by 6.844 units. This interpretation is true only if the effects of other variables in the model are held constant. The t-test
: This value indicates that as burden at bench toe increases by one unit, blasthole productivity increases by 6.844 units. This interpretation is true only if the effects of other variables in the model are held constant. The t-test 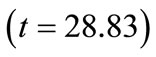 associated with this value indicates that it is significant
associated with this value indicates that it is significant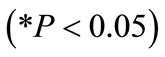 . Burden at bench is making a significant contribution to the model.
. Burden at bench is making a significant contribution to the model.
2) Blasthole spacing : This value indicates that as blasthole spacing increases by one unit, blasthole productivity decreases by 15.028 units. This interpretation is true only if the effects of other variables in the model are held constant. The t-test
: This value indicates that as blasthole spacing increases by one unit, blasthole productivity decreases by 15.028 units. This interpretation is true only if the effects of other variables in the model are held constant. The t-test 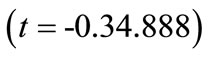 associated with this value indicates that it is significant
associated with this value indicates that it is significant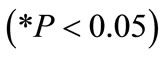 . Average blasthole spacing is making a significant contribution to the model.
. Average blasthole spacing is making a significant contribution to the model.
3) Powder factor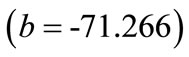 : This value indicates that as powder factor increases by one unit, blasthole productivity decreases by 71.266 units. This interpretation is true only if the effects of other variables in the model are held constant. The t-test
: This value indicates that as powder factor increases by one unit, blasthole productivity decreases by 71.266 units. This interpretation is true only if the effects of other variables in the model are held constant. The t-test 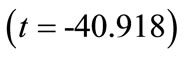 associated with this value indicates that it is significant
associated with this value indicates that it is significant . Powder factor is making a significant contribution to the model.
. Powder factor is making a significant contribution to the model.
4) Compressive rock strength : This value indicates that as average rock hardness increases by one unit, blasthole productivity decreases by 1.781 units. This interpretation is true only if the effects of other variables in the model are held constant. The t-test
: This value indicates that as average rock hardness increases by one unit, blasthole productivity decreases by 1.781 units. This interpretation is true only if the effects of other variables in the model are held constant. The t-test
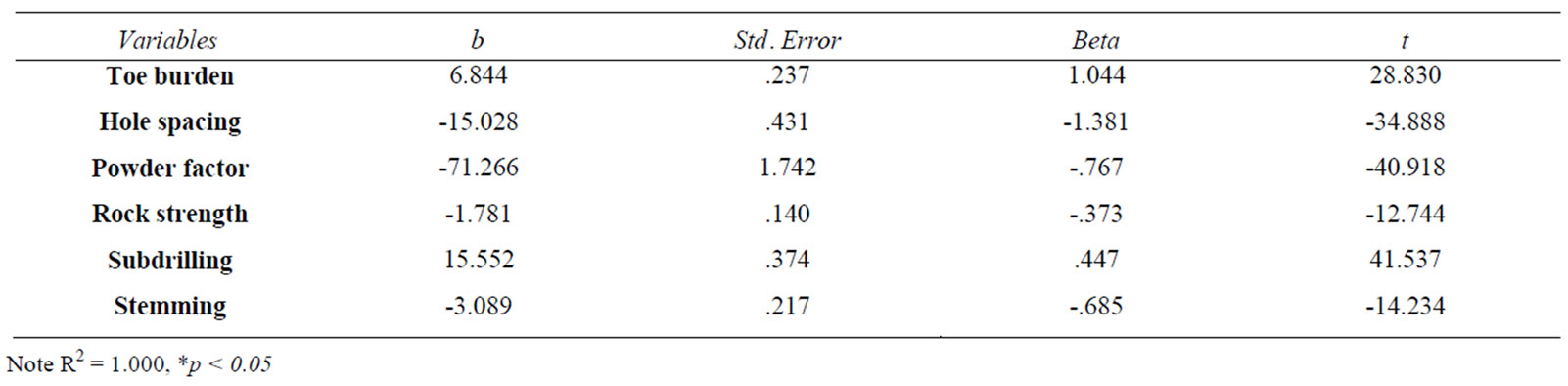
Table 3. Significant variables and their coefficients.
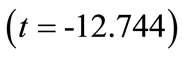 associated with this value indicates that it is significant
associated with this value indicates that it is significant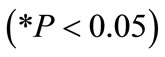 . Rock hardness is making a significant contribution to the model.
. Rock hardness is making a significant contribution to the model.
5) Subdrilling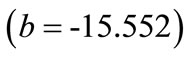 : This value indicates that as subdrilling increases by one unit, blasthole productivity increases by 15.552 units. This interpretation is true only if the effects of other variables in the model are held constant. The t-test
: This value indicates that as subdrilling increases by one unit, blasthole productivity increases by 15.552 units. This interpretation is true only if the effects of other variables in the model are held constant. The t-test 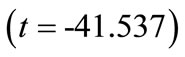 associated with this value indicates that it is significant
associated with this value indicates that it is significant . Subdrilling is making a significant contribution to the model.
. Subdrilling is making a significant contribution to the model.
6) Stemming height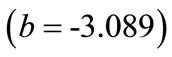 : This value indicates that as average stemming increases by one unit, blasthole productivity decreases by 3.089 units. This interpretation is true only if the effects of other variables in the model are held constant. The t-test
: This value indicates that as average stemming increases by one unit, blasthole productivity decreases by 3.089 units. This interpretation is true only if the effects of other variables in the model are held constant. The t-test  associated with this value indicates that it is significant
associated with this value indicates that it is significant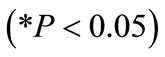 . Stemming height is making a significant contribution to the model.
. Stemming height is making a significant contribution to the model.
7) Rock density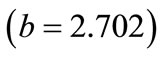 : This value indicates that as rock density increases by one unit, blasthole productivity increases by 2.702 units. This interpretation is true only if the effects of other variables in the model are held constant. The t-test
: This value indicates that as rock density increases by one unit, blasthole productivity increases by 2.702 units. This interpretation is true only if the effects of other variables in the model are held constant. The t-test  associated with this value indicates that it is not significant
associated with this value indicates that it is not significant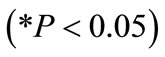 . The contribution of the rock density to the model is not significant and therefore was removed from the model.
. The contribution of the rock density to the model is not significant and therefore was removed from the model.
8) Volume of rock blasted per blast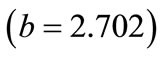 : This value indicates that as volume of rock blasted per blast increases by one unit, blasthole productivity increases by 2.702 units. This interpretation is true only if the effects of other variables in the model are held constant. The t-test
: This value indicates that as volume of rock blasted per blast increases by one unit, blasthole productivity increases by 2.702 units. This interpretation is true only if the effects of other variables in the model are held constant. The t-test 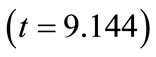 associated with this value indicates that it is not significant
associated with this value indicates that it is not significant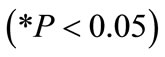 . The contribution of the volume of rock blasted to the model was not significant and therefore was removed from the model.
. The contribution of the volume of rock blasted to the model was not significant and therefore was removed from the model.
Model 3: Maximum blasting Cost, RUB/T
The value of R2 is 0.993 showing that the seven predictors entered in the regression analysis account for 99.3% of the variation in the maximum blasting cost per cubic meter of blasting, while the F change is 40.617 and is greater than one showing that the model is signifycantly better at predicting the maximum cost than using the mean as the best guess (significant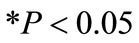 ). The variables found to be significant for the maximum blasting cost, RUB/T include: Compressive rock strength, rock density, volume of rock blasted per blast and burden at bench toe. The other variables which were included in the analysis: bench height, powder factor and blasthole spacing were not found to be significant and are not shown on Table 4.
). The variables found to be significant for the maximum blasting cost, RUB/T include: Compressive rock strength, rock density, volume of rock blasted per blast and burden at bench toe. The other variables which were included in the analysis: bench height, powder factor and blasthole spacing were not found to be significant and are not shown on Table 4.
Explanation of each variable and their coefficients
1) Compressive rock strength : This value indicates that as compressive rock strength increases by one unit, maximum blasting cost increases by 39.89 units. This interpretation is true only if the effects of other variables in the model are held constant. The t-test associated with this value indicates that it is significant
: This value indicates that as compressive rock strength increases by one unit, maximum blasting cost increases by 39.89 units. This interpretation is true only if the effects of other variables in the model are held constant. The t-test associated with this value indicates that it is significant . Compressive rock strength is making a significant contribution to the model.
. Compressive rock strength is making a significant contribution to the model.
2) Rock density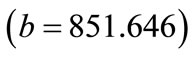 : This value indicates that as rock density increases by one unit, maximum blasting cost decreases by 851.65 units. This interpretation is true only if the effects of other variables in the model are held constant. The t-test associated with this value indicates that it is not significant
: This value indicates that as rock density increases by one unit, maximum blasting cost decreases by 851.65 units. This interpretation is true only if the effects of other variables in the model are held constant. The t-test associated with this value indicates that it is not significant . Rock density is making a significant contribution to the model.
. Rock density is making a significant contribution to the model.
3) Volume of rock blasted per blast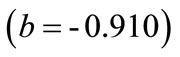 : This value indicates that as volume of rock blasted per blast increases by one unit, maximum blasting cost decreases by 0.91 units. This interpretation is true only if the effects of other variables in the model are held constant. The t-test associated with this value indicates that it is significant
: This value indicates that as volume of rock blasted per blast increases by one unit, maximum blasting cost decreases by 0.91 units. This interpretation is true only if the effects of other variables in the model are held constant. The t-test associated with this value indicates that it is significant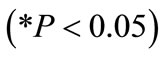 . The volume of rock blasted per blast is making a significant contribution to the model.
. The volume of rock blasted per blast is making a significant contribution to the model.
4) Burden at bench toe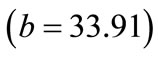 : This value indicates that as burden at bench toe increases by one unit, maximum blasting cost decreases by 33.91 units. This interpretation is true only if the effects of other variables in the model are held constant. The t-test associated with this value indicates that it is significant
: This value indicates that as burden at bench toe increases by one unit, maximum blasting cost decreases by 33.91 units. This interpretation is true only if the effects of other variables in the model are held constant. The t-test associated with this value indicates that it is significant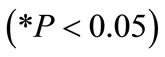 . Burden at bench toe is making a significant contribution to the model.
. Burden at bench toe is making a significant contribution to the model.

Table 4. Significant variables and their coefficients.
5) Bench height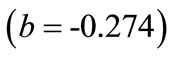 : This value indicates that as bench height increases by one unit, maximum blasting cost decreases by 0.274 units. This interpretation is true only if the effects of other variables in the model are held constant. The t-test
: This value indicates that as bench height increases by one unit, maximum blasting cost decreases by 0.274 units. This interpretation is true only if the effects of other variables in the model are held constant. The t-test 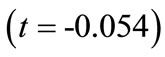 associated with this value indicates that it is not significant
associated with this value indicates that it is not significant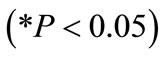 . The contribution of bench height to the model is not significant and therefore was removed from the model.
. The contribution of bench height to the model is not significant and therefore was removed from the model.
6) Powder factor : This value indicates that as powder factor increases by one unit, maximum blasting cost increases by 362.11 units. This interpretation is true only if the effects of other variables in the model are held constant. The t-test
: This value indicates that as powder factor increases by one unit, maximum blasting cost increases by 362.11 units. This interpretation is true only if the effects of other variables in the model are held constant. The t-test  associated with this value indicates that it is not significant
associated with this value indicates that it is not significant . The contribution of the powder factor to the model is not significant and therefore was removed from the model.
. The contribution of the powder factor to the model is not significant and therefore was removed from the model.
7) Blasthole spacing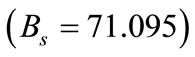 : This value indicates that as blasthole spacing increases by one unit, maximum blasting cost increases by 71.10 units. This interpretation is true only if the effects of other variables in the model are held constant. The t-test
: This value indicates that as blasthole spacing increases by one unit, maximum blasting cost increases by 71.10 units. This interpretation is true only if the effects of other variables in the model are held constant. The t-test 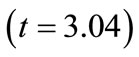 associated with this value indicates that it is not significant
associated with this value indicates that it is not significant . The contribution of the blasthole spacing to the model is not significant and therefore was removed from the model.
. The contribution of the blasthole spacing to the model is not significant and therefore was removed from the model.
The estimated regression models for the assessment of oversize generation, blasthole productivity and blasting cost for iron ore surface blasting are as shown on formulas (5), (6) and (7) respectively.
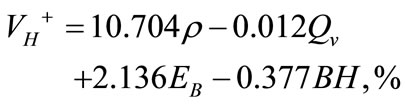 (5)
(5)
 (6)
(6)
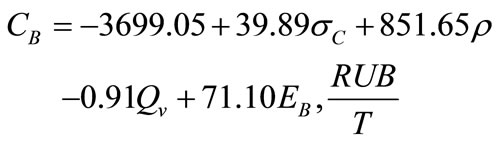 (7)
(7)
4. Discussion of Results
The impact of rockmass and blast design parameters on the effectiveness of iron ore surface blasting could be explained in accordance to the estimated regression models obtained for oversize generation, blasthole productivity and blasting cost as follows:
4.1. Rock Density
As rock density increases, generation of oversize increases, resulting to the increase of blasting cost on secondary blasting. Several authors including [2,11] also noted that rock density hampers the transfer of energy into the rock mass and thus the blastability, fragmentation and cost of blasting.
4.2. Compressive Rock Strength
As compressive rock strength increases, blasthole productivity decreases, resulting to the increase of blasting cost due to the decrease of blasthole productivity. As the compressive rock strength increases, rocks become harder to break, resulting to the decrease of blasthole productivity.
4.3. Powder Factor
As powder factor increases, blasthole productivity decreases because as powder factor increases, stemming height decreases and the energy wasted on blown out holes also increases. However, the increase of blasting cost due to the increase of powder factor is not significant because the powder factors assessed are closely marched with the rockmass and other blast design parameters of the mines.
4.4. Burden at Bench Toe
As burden at bench toe increases, productivity of blasthole increases, however, effect on blasting cost is positive but insignificant probably because change itself is not significant.
4.5. Blasthole Spacing
As blasthole spacing increases, oversize generation increases and blasthole productivity goes down because, as blasthole spacing increases, utilization of the collective rock crushing capability of neighboring blastholes on the middle of their spacing decreases. As a consequence the observed increase of blasting cost is associated with the increase of secondary blasting and the decrease of blasthole productivity arising from the underutilization of the collective rock crushing capability of neighboring blastholes.
4.6. Stemming Height
As stemming height increases, blasthole productivity decreases because change is accompanied by poor fragmentation of the upper parts of benches. However, change and its effect are small and not felt on the cost of blasting.
4.7. Subdrilling
As subrilling increases, blasthole productivity increases but changes are small and not felt on the degree of fragmentation and the cost of blasting.
4.8. Bench Height
The increase of bench height reduces oversize generation because as bench height increases, the easy to displace and deform rock also increases as noted by Ash (1977). However change is small and its effect on blasting cost improvement is not significant.
4.9. Volume of Rock Blasted per Blasting Round
As the volume of rock blasted per blast increases, oversize generation and blasting cost decreases because as volume increases number of blastholes and rows fired in one blast also increases and as a result increases the secondary fragmentation caused by the collisions of rock masses moving from the increased number of blasthole and rows.
The above interpretation allows concluding that the individual effects of the investigated parameters of rockmass and blast design parameters on oversize generation, blasthole productivity and blasting cost are in compliance with the findings of other researchers and the theory of explosive rock fragmentation.
5. Conclusions and Recommendations
The regression models developed here could be used for the estimation of oversize generation, blasthole productivity and blasting cost in rockmass and blast design conditions similar to those of the 10 large scale iron ore surface mines examined in this paper.
However, alone, the regression models obtained here could not be used for the optimization of blast design because most of the determinant parameters also have conflicting effect on the other processes of the rock blasted in drilling, handling and primary crushing. Also the quality and content of the regression models could be enhanced further by increasing the content of rockmass and blast design parameters and the volume of data considered in the regression analysis.
6. REFERENCES
- F. A. Avdyeev, V. L. Baron, N. V. Gurov and V. X. Kantor, “Drilling and Blasting Specifications Handbook,” Nedra, Moscow, 1986.
- B. Bahman, “The Effects of Geological Parameters onRock Blasting Using the Hopkinson Split Bar,” International Journal of Rock Mechanics and Mining Sciences, Vol. 34, No. 3-4, April-June 1997, pp. 32.e1-32.e9. doi:10.1016/S1365-1609(97)00228-1
- L. J. Carlos, L. J. Emilio and J. A. C. Fransisco, “Drilling and Blasting of Rocks,” Balkema, Rotterdam, 1995.
- Department of the Army-U.S. Army Corps of Engineers, “Engineer Manual/Engineering & Design/Systematic Drilling and Blasting for Surface Excavations,” EM1110- 3800, Washingtonne D.C., 1 March 1972.
- C. H. Dowding and C. T. Aimone, “Rock Breakage: Explosives,” SME Mining Engineering Handbook, Sacramento, 1992.
- M. F. Drukovani, L.V. Dubnov, B. N. Kutuzov and I. Efremov, “Surface Drilling & Blasting Handbook,’’ Naukova Dumka, Kiev, 1973.
- R. Gustafson, “Swedish Blasting Technique (Russian translation),” Nedra, Moscow, 1977.
- V. S. Harikov, “Surface Mining of Mineral Resource Deposits,’’ Nedra, Moscow, 1982.
- J.-P. Latham and P. Lu., “Development of an Assessment System of Blastability for Rock Masses,’’ International Journal of Rock Mechanics and Mining Sciences, Vol. 36, No. 1, January 1999, pp. 41-55. doi:10.1016/S0148-9062 (98)00175-2
- B. N. Kutuzov, “Blasting Works,” Nedra, Moscow, 1988.
- B. N. Kutuzov, B. I. Komashenko, B. F. Noskov, C. B. Gabrahamov and A. A. Muzirkov, “Lab and Practical Exercises in the Explosive Breakage of Rocks,’’ Nedra, Moscow, 1981.
- A. T. S. Massawe, “Drilling & Blasting Part I: Blasting Manual,” LAP LAMBERT Academic Publishing AG & Co.KG, Saarbrucken, 2010.
- A. G. Protosenya, C. A. Kulish, E. I. Azbel, K. D. Naumenko, V. B. Sivui and B. Z. Bezmozgin, “Mathematical Methods and Models in Mining Production Planning and Control,” Nedra, Moscow, 1985.

Appendix: Data variations of iron ore large scale mines in the former Soviet Union.

