Intelligent Control and Automation
Vol.4 No.4(2013), Article ID:39505,6 pages DOI:10.4236/ica.2013.44046
Observer for Linear Distributed-Parameter Systems with Application to Isothermal Plug-Flow Reactor
1LINMA, Department of Mathematics, Faculty of Sciences, Université Chouaib Doukkali, El Jadida, Morocco
2CESAME, Université Cathoulique de Louvain, Louvain-La-Neuve, Belgium
Email: nbarje@yahoo.fr
Copyright © 2013 N. Barje et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received July 27, 2013; revised August 27, 2013; accepted September 5, 2013
Keywords: Distributed-Parameter Systems; 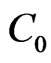 -semigroup; Exponential Observers; Perturbed Systems; Tubular Reactor
-semigroup; Exponential Observers; Perturbed Systems; Tubular Reactor
ABSTRACT
This paper presents a conception of an exponential observer for a class of linear distributed-parameter systems (DPSs), in which the dynamics are partially unknown. The given distributed-parameter observer ensures asymptotic state estimator with exponentially decay error, based on the theory of 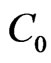 -semigroups in a Hilbert space. The theoretical observer developed is applied to a chemical tubular reactor, namely the isothermal Plug-Flow reactor basic dynamical model for which measurements are available at the reactor output only. The process is described by Partial differential equations with unknown initial states. For this application, performance issues are illustrated in a simulation study.
-semigroups in a Hilbert space. The theoretical observer developed is applied to a chemical tubular reactor, namely the isothermal Plug-Flow reactor basic dynamical model for which measurements are available at the reactor output only. The process is described by Partial differential equations with unknown initial states. For this application, performance issues are illustrated in a simulation study.
1. Introduction
In many physical systems (e.g., bio-reactor, vibrations problems in mechanics, diffusion problems), the states of the mathematical model depend on spatial variable, which is a position in a one-dimensional or multi-dimensional space. This kind of system is called distributedparameter system(s) (DPSs) (see [1]). A powerful tool in the analysis of DPSs is the theory of  -semigroups (see [2,3]).
-semigroups (see [2,3]).
For the state feedback control, the exact and full knowledge of sates of the system is important. However, the presence of spatial variables makes the state not available for direct measurements and that imposes limitations to the design. In such case, the states can be estimated using state estimators (observers). For this purpose, the classical theory of the Luenberger observer [4] has been extended from linear finite-dimensional systems to a large class of DPSs by many authors, (we mention as examples [5-10] and the references within). However, research on efficient and practicable observer design for DPSs has not been so extensive as in the case of finitedimensional systems, and papers on distributed-parameter observers are scattered in the literature.
In This paper, we focus on estimating the states of linear DPSs with partially unknown dynamics. The paper presents an exponential distributed-parameter observer design which is an asymptotic state estimator with exponentially decay error. The proposed conception is efficient and suitable in practice applications; for instance, it is appropriate to be applied to estimate the states of a chemical tubular reactor, namely the isothermal PlugFlow Reactor basic dynamical model, with unknown initial state, in the case where measurements may occur at the reactor output only.
2. Infinite Dimensional Observer Design
Let consider the linear Infinite-Dimensional system given by
 (1)
(1)
Here, 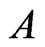 is the infinitesimal generator of a
is the infinitesimal generator of a  - semigroup on a real Hilbert space
- semigroup on a real Hilbert space 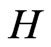 with inner product
with inner product  and the induced norm
and the induced norm ,
, 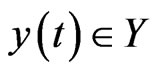 is the known output function associated to the unknown initial condition
is the known output function associated to the unknown initial condition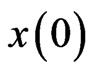 ,
, 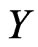 is another real Hilbert space and
is another real Hilbert space and 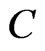 is a bounded linear operator from
is a bounded linear operator from  into
into . The dot over a variable means the time derivative of the variable.
. The dot over a variable means the time derivative of the variable.
The purpose is to design a dynamic system (observer or state estimator) for the system (1) by using  as the input such that the output of this designed dynamic system is used as an estimate of the current state
as the input such that the output of this designed dynamic system is used as an estimate of the current state 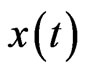 of (1).
of (1).
The initial state  of (1) is unknown while the initial state
of (1) is unknown while the initial state 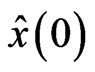 of the observer can be assigned arbitrarily. Thus, the error between
of the observer can be assigned arbitrarily. Thus, the error between  and
and  is still an unknown quantity even if we know
is still an unknown quantity even if we know . As a basic requirement in observer design, we require that if
. As a basic requirement in observer design, we require that if 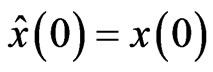 then
then  for all
for all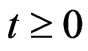 . So, the observer for (1) can be expressed in the following form
. So, the observer for (1) can be expressed in the following form
 (2)
(2)
where 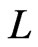 is the observer gain operator.
is the observer gain operator.
Proposition 2.1: Given the linear infinite-dimensional system (1). Suppose that there exists a bounded linear operator  from
from 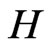 into
into 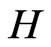 such that the linear operator
such that the linear operator  is the infinitesimal generator of a
is the infinitesimal generator of a 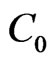 - semigroup
- semigroup 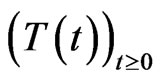 on
on , such that there exist constants
, such that there exist constants 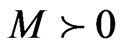 and
and 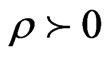 and a time
and a time  satisfying:
satisfying:
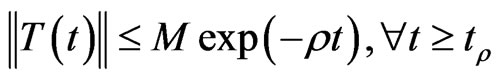
then the dynamic system (2) with 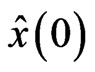 arbitrary chosen is an exponential observer for system (1) and
arbitrary chosen is an exponential observer for system (1) and
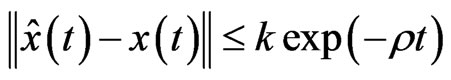
for all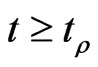 , where
, where  is a positive number depending on
is a positive number depending on .
.
Proof 1 Let consider the estimation error  , for all
, for all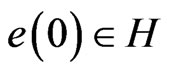 , the evolution system,
, the evolution system,
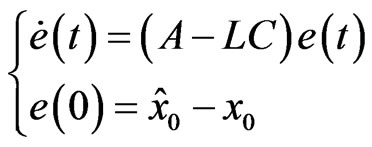 (3)
(3)
has a unique mild solution on the interval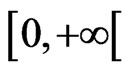 , given by:
, given by: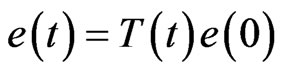 , for all
, for all 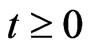 (see [2,3]).
(see [2,3]).
Hence,

Thus, the error satisfies:
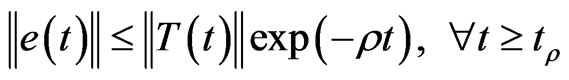
and that implies that the norm of the difference  will decrease exponentially to zero. This competes the proof.
will decrease exponentially to zero. This competes the proof.
Let now suppose that linear operator  is the infinitesimal generator of a
is the infinitesimal generator of a  -semigroup
-semigroup  and
and  is linear bounded operator on
is linear bounded operator on . The following result will be needed in the sequel.
. The following result will be needed in the sequel.
Theorem 2.2: [3] The operator 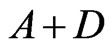 is the infinitesimal generator of a
is the infinitesimal generator of a  -semigroup
-semigroup  which is the unique solution of the equation
which is the unique solution of the equation

for all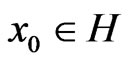 . If in addition,
. If in addition, 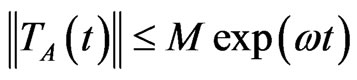 , then,
, then,
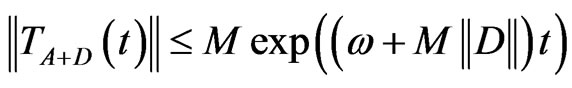
3. Application to the Plug-Flow Reactor Basic Model
The theory presented in the linear infinite-dimensional sitting in Section 2, is applied to reconstruct the states of a chemical tubular reactor with the following chemical reaction:
 (4)
(4)
where  is the reactant,
is the reactant, 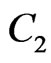 the product, and
the product, and 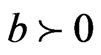 is the stoichiometric coefficient of the reaction. The dynamics of the process in a tubular reactor without axial dispersion are given, for all time
is the stoichiometric coefficient of the reaction. The dynamics of the process in a tubular reactor without axial dispersion are given, for all time  and for all
and for all 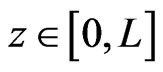 where
where  is the reactor length, by mass balance equations (see [11]):
is the reactor length, by mass balance equations (see [11]):
 (5)
(5)
with the boundary conditions:
 (6)
(6)
and the initial conditions:
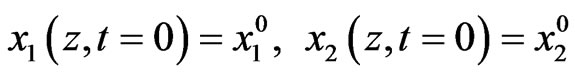 (7)
(7)
where  and
and 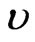 are the concentrations of
are the concentrations of  and
and  (mol/l), the influent reactant concentration (mol/l) and the fluid superficial velocity (m/s). We assume that the kinetics depend only on the reactant concentration
(mol/l), the influent reactant concentration (mol/l) and the fluid superficial velocity (m/s). We assume that the kinetics depend only on the reactant concentration 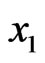 and we consider a reaction rate model of the form
and we consider a reaction rate model of the form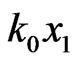 , where
, where  is the kinetic constant
is the kinetic constant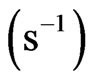 .
.  denotes a finite unit impulse of window width w, i.e. an approximate Dirac delta distribution at
denotes a finite unit impulse of window width w, i.e. an approximate Dirac delta distribution at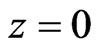 , given by
, given by
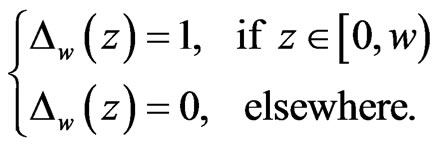
The initial states  are supposed to be unknown hereafter.
are supposed to be unknown hereafter.
Throughout the sequel, we assume  , the Hilbert space with the usual inner product
, the Hilbert space with the usual inner product

and the induced norm
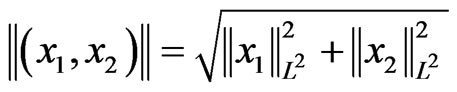
for all  and
and  in
in .
.
A partial-differential equations like (5)-(7), when expended with an output equation, can also be expressed as an abstract state space equation on the Hilbert space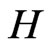 :
:
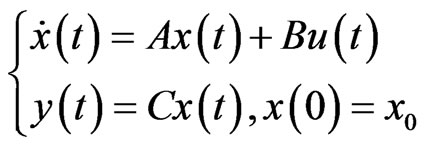 (8)
(8)
associated to the unknown initial condition  . Where,
. Where, 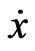 stands for the time derivative of the state
stands for the time derivative of the state , and the control
, and the control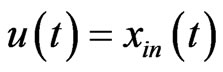 . The control operator
. The control operator 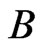 is a bounded linear operator from
is a bounded linear operator from  to
to , which is defined by
, which is defined by

The output trajectory  is a bounded linear operator, and the linear operator
is a bounded linear operator, and the linear operator  is defined on its domain,
is defined on its domain,

by,

The operator  is the infinitesimal generator of a
is the infinitesimal generator of a  -semigroup
-semigroup 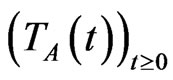 on
on , exponentially stable, i.e., there exist constants
, exponentially stable, i.e., there exist constants 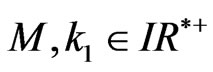 such that,
such that,
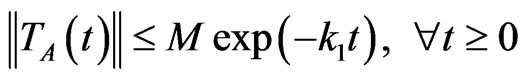
Satisfying,
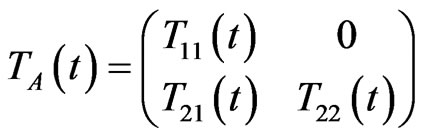
such that for all , (see [11] and the references within for more detail),
, (see [11] and the references within for more detail),

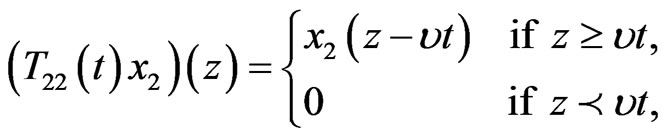
and

Remark 3.1 [11] It can be observed that the  semigroup
semigroup  is such that
is such that 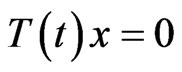 for all
for all
 , for all
, for all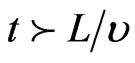 , whence the stability bound is rather conservative and is only of interest for t small.
, whence the stability bound is rather conservative and is only of interest for t small.
More specifically, Remark 3.1 could lead us to deduce intuitively that the growth bound  of the
of the  -semigroup
-semigroup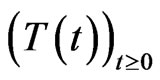 , defined as follows:
, defined as follows:

is equal to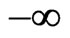 .
.
3.1. Observer Design
Hereafter we consider measurements of the state vector  are available at the reactor output only. In this case, the output function
are available at the reactor output only. In this case, the output function  is defined as follows: we consider a (very small) finite interval at the reactor output
is defined as follows: we consider a (very small) finite interval at the reactor output  such that:
such that:
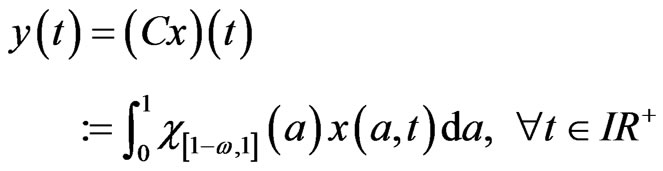 (9)
(9)
where,  if
if 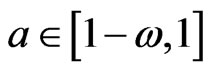 and
and  elsewhere, with
elsewhere, with  is a small number.
is a small number.
The observer operator  is linear bounded.
is linear bounded.
For all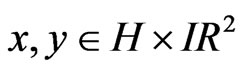 ,
,
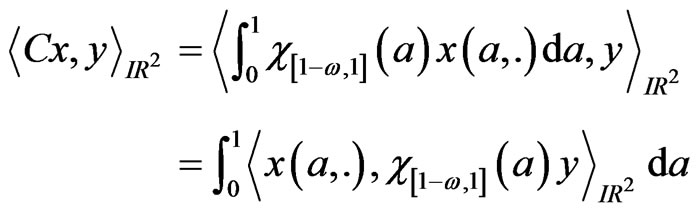
The adjoint operator 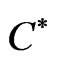 of
of 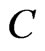 is defined for all
is defined for all 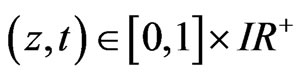 by:
by:
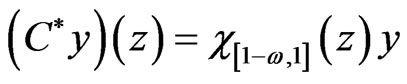
For all 

Then, 
A candidate observer for the system (5)-(7), is obtained as the output of the following dynamic system
 (10)
(10)
with the boundary conditions:
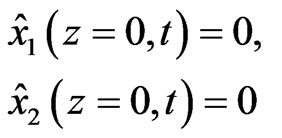 (11)
(11)
and the initial conditions:
 (12)
(12)
With 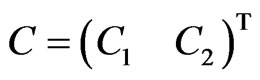 defined by (9) and g the is a positive number.
defined by (9) and g the is a positive number.
The system (10)-(12) can be written on its compact form
 (13)
(13)
where, the linear operator  is the observer gain, satisfy
is the observer gain, satisfy
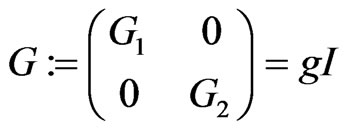 (14)
(14)
with  is the identity operator of the Hilbert
is the identity operator of the Hilbert .
.
Corollary 3.1: Given the isothermal Plug-Flow reactor basic dynamical model (5)-(7). Suppose that there exists a bounded linear operator , where
, where  is a positive number, such that
is a positive number, such that , the dynamic system (10)-(12) is an exponential observer for the system (5)-(7).
, the dynamic system (10)-(12) is an exponential observer for the system (5)-(7).
Proof 2 Let consider the linear operator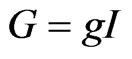 , where
, where  is a positive number. The operator
is a positive number. The operator 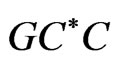 is a bounded linear operator on
is a bounded linear operator on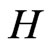 , such that
, such that
 .
.
On the other hand, from Remark 3.1 and the definition of the growth bound, there exists a time  such that
such that

Hence,

Now, by the Theorem 2.2, the linear operator  is the infinitesimal generator of a
is the infinitesimal generator of a  -semigroup
-semigroup 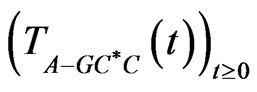 satisfying, for all
satisfying, for all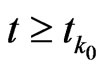 :
:
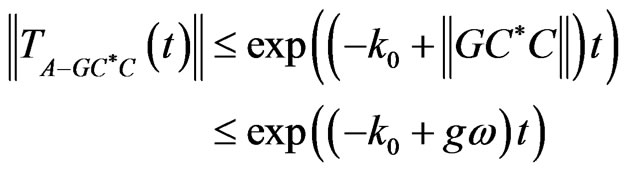
If , it follows by application of the Theorem 2.1that the dynamic system (10)-(12) is an exponential observer for the system (5)-(7). More precisely the reconstruction error
, it follows by application of the Theorem 2.1that the dynamic system (10)-(12) is an exponential observer for the system (5)-(7). More precisely the reconstruction error  satisfies, for all
satisfies, for all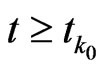 ,
,

3.2. Simulation Result
In order to test the performance of the proposed observer, numerical simulations will be given. The equations have been integrated by using a backward finite difference approximation for the first-order space derivative . The adopted numerical values for the process parameters are taken from the Table 1 (see [12]).
. The adopted numerical values for the process parameters are taken from the Table 1 (see [12]).
Figures 1 and 2 show respectively the evolution in time and space of the error on the reactant concentration  and the evolution in time and space of the error on the product concentration
and the evolution in time and space of the error on the product concentration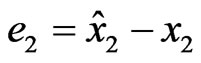 , related to the observer (10)-(12).
, related to the observer (10)-(12).
The measurements are taken on the length interval 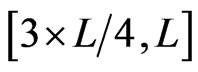 i.e.,
i.e., 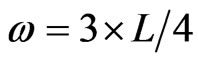 , and the process model has been arbitrary initialized with the constant profiles
, and the process model has been arbitrary initialized with the constant profiles  and
and . In order to response to the assumption of the Corollary 3.1we set
. In order to response to the assumption of the Corollary 3.1we set  for the observer design parameter.
for the observer design parameter.
4. Conclusions and Prospects
In this paper we present a conception of a state estimator for linear distributed-parameter systems, which ensures that the estimation error converges exponentially to zero. The theory developed is applied to reconstruct the state of the isothermal Plug-Flow reactor basic dynamical model, and performed by a simulation study in which the parameters can be tuned by the user to satisfy specific needs in terms of convergence rate.
One of the purposes in designing an observer is to obtain an efficient and practicable feedback control that stabilizes the original system around a desired profile. So the investigation of the stability of the overall closedloop system (which is composed of original system, ob-
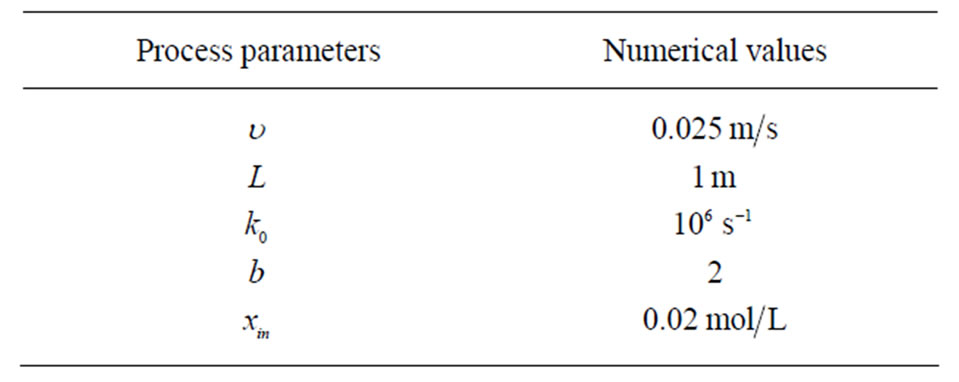
Table 1. Process parameters for numerical simulations.

Figure 1. Error evolution of the reactant concentration.

Figure 2. Error evolution of the product concentration.
server, and feedback controller), is an interesting topic for future research.
5. Acknowledgements
This paper presents research results of the Moroccan “Programme Thématique d’Appui à la Recherche Scientifique” PROTARS III, initiated by the Moroccan “Centre National de la Recherche Scientifique et Technique”
(CNRST). The work is also supported by the Belgian Programme on Interuniversity Poles of Attraction (PAI).
REFERENCES
- M. Renardy and R. C. Rogers,” An Introduction to Partial Dif ferential Equations,” Springer, New York, 1993.
- A. Pazy, “Semigroups of Linear Operators and Applications to Partial Differential Equations,” Springer-Verlag, New York, 1983. http://dx.doi.org/10.1007/978-1-4612-5561-1
- R. F. Curtain and J. Zwart, “An Introduction to Infinite Dimentional Linear Systems Theory,” Springer, New York, 1995. http://dx.doi.org/10.1007/978-1-4612-4224-6
- D. Luenberger, “An Introduction to Observers,” IEIEEE Transactions on Automatic Control, Vol. 16, No. 6, 1971, pp. 596-602. http://dx.doi.org/10.1109/TAC.1971.1099826
- T. Kobayashi and S. Hitotsuya, “Observers and Parameter Determination for Distributed Parameter Systems,” International Journal of Control, Vol. 33, No. 1, 1981, pp. 31-50. http://dx.doi.org/10.1080/00207178108922906
- A. VandeWouwer and M. Zeitz, “State Estimation in Distributed Parameter Systems,” In: Encyclopedia of Life Support Systems (EOLSS): Control Systems, Robotics and Automation. EOLSS Publishers, London, 2003.
- M. A. Demetriou, “Natural Second-Order Observers for Second-Order Distributed Parameter Systems,” Systems & Control Letters, Vol. 51, No. 3-4, 2004, pp. 225-234. http://dx.doi.org/10.1016/j.sysconle.2003.08.005
- A. Smyshlyaev and M. Krstic, “Backstepping Observers for a Class of Parabolic PDEs,” Systems & Control Letters, Vol. 54, No. 7, 2005, pp. 613-625. http://dx.doi.org/10.1016/j.sysconle.2004.11.001
- T. D. Nguyen, “Second-Order Observers for SecondOrder Distributed Parameter Systems in R2,” Systems & Control Letters, Vol. 57, No. 10, 2008, pp. 787-795. http://dx.doi.org/10.1016/j.sysconle.2008.03.011
- R. Miranda, I. Chairez and J. Moreno, “Observer Design for a Class of Parabolic PDE via Sliding Modes and Backstepping,” Proceedings of International Workshop on Variable Structure Systems, Mexico City, Jun 2010, pp. 215-220.
- J. Winkin, D. Dochain and P. Ligarius, “Dynamical Analysis of Distributed Parameter Tubular Reactors,” Automatica, Vol. 36, No. 3, 2000, pp. 349-361. http://dx.doi.org/10.1016/S0005-1098(99)00170-3
- I. Y. Smets, D. Dochain and J. F. Van Impe, “Optimal Temperature Control of a Steady-State Exothermic PlugFlow Reactor,” AIChE Journal, 2002, Vol. 48, No. 2, pp. 279-286. http://dx.doi.org/10.1002/aic.690480212

