Intelligent Control and Automation
Vol. 4 No. 3 (2013) , Article ID: 35563 , 8 pages DOI:10.4236/ica.2013.43035
Design and Analysis of a Sliding Table Controller for Diabetes
1The College of Industrial Technology, Misurata, Libya
2The University of Misurata, Misurata, Libya
Email: ahmed_bensasi@yahoo.co.uk, elmalki_m@yahoo.com
Copyright © 2013 Ahmed Y. Ben Sasi, Mahmud A. Elmalki. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received May 14, 2013; revised June 14, 2013; accepted June 21, 2013
Keywords: Sliding Table Controller; PID Controller; Blood Glucose-Insulin System; Diabetes
ABSTRACT
A discrete insulin infusion based on long-time interval measurement is the classic technique for diabetes treatment. Nevertheless, in this research, a closed-loop control system was proposed for continuous drug infusion to overcome the drawbacks of these typical discrete methods and develop more practical diabetes therapy systems. A blood glucoseinsulin system was implemented relying on continuous insulin injection model. Based on this model, two controllers were designed to deal with the control dilemma of the resulting highly nonlinear plant. The controllers designed in this paper are: proportional integral derivative (PID), and sliding table controllers. Simulation results have shown that the sliding table controller can outperform the PID controller even with severe circumstances of disturbance in glucose, such as exercise, delay or noise in glucose sensor and nutrition mixed meal absorption at meal times.
1. Introduction
Many researchers have attempted to find methods for diagnosing and treating diabetes disease. One of the approaches is to design an automated closed-loop insulin delivery system. A fully automated closed-loop insulin delivery system (also known as an artificial pancreas) could potentially be the ultimate answer for blood glucose control in diabetic patients. This system can mimic the activity of a normal pancreas and is capable of maintaining physiological blood glucose levels for insulindependent diabetic patients.
Such an artificial pancreas system can theoretically produce tight glucose control without finger-stick blood glucose measurements, subcutaneous insulin injections, or hypo-/hyper-glycemic events, thereby dramatically improving the quality of life for an insulin-dependent diabetic patient. The artificial pancreas is a system of integrated devices containing only synthetic materials, which substitutes for a pancreas by sensing plasma glucose concentration, calculating the amount of insulin needed, and then delivering the correct amount of insulin. Typically, such a device is comprised of a glucose monitoring sensor, an insulin pump, and a control algorithm to regulate the pump to deliver the insulin in order to maintain the normality of glycemia in presence of sensor measurements.
Figure 1 shows a basic block diagram of this type of closed-loop control for the regulation of glucose levels. In this figure, a controller receives the difference between the glucose set point (desired BG) and the glucose reading, and uses this information to continuously adjust the rate of insulin delivery. This closed-loop control is very similar to the function that is performed by a healthy human pancreas; in other words, the research’s aim is to design a device that essentially functions as an artificial pancreas.
2. The Mathematical Model of a Diabetic Patient
In order to have a reliable model-based automatic insulin delivery system operating under various physiological conditions, a model must be synthesized that has glucose-predicting ability and includes all the major energyproviding substrates at rest, as well as during physical activity. The mathematical models of metabolism proposed to use, in this paper, glucose-based and have the contribution of free fatty acid (FFA) metabolism, which is an important source of energy for the body. Also,
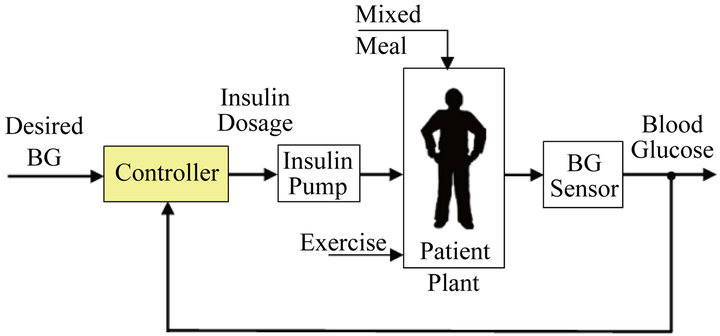
Figure 1. Block diagram of closed-loop insulin delivery system.
significant interactions exist among FFA, glucose, and insulin. Figure 2 shows the simulation of a composite model which is capable of predicting FFA-glucose-insulin dynamics during rest and exercise [1-4].
It is important to consider these metabolic interactions in order to characterize the endogenous energy production of a healthy or diabetic patient. In addition, physiological exercise induces fundamental metabolic changes in the body. A mixed meal model was developed to capture the absorption of carbohydrates (CHO), proteins, and FFA from the gut into the circulatory system. The mixed meal model served as a disturbance to the proposed model. An exercise model was used to incorporate the effects of exercise on glucose and insulin dynamics to capture the changes in glucose and insulin dynamics during and after mild-to-moderate exercise [5-7].
A composite model capable of predicting FFA-glucose-insulin dynamics during rest and exercise was developed by Anirban Roy, in his Ph.D. dissertation [1], where the model successfully captured the FFA-glucose interactions at the systemic level, and also successfully predicted mild-to-moderate exercise effects on glucose and FFA dynamics. Because of this very nature, the composite model was selected in this work to provide a platform for the development of close loop controllers to maintain glucose homeostasis of a diabetic patient.
3. Controllers Design and Simulation
Our studies have focused on using of the mathematical composite model in section two to developing two control algorithms: the PID and Sliding table control using Matlab/Simulink. The target blood glucose range that the controllers were supposed to attain and maintain is similar to healthy blood-glucose levels are between 70 mg/dL and 120 mg/dL before meals and less than 180 mg/dL after meals [2,3].
3.1. PID Controller
The most traditional of all controllers is probably the proportional-integral-derivative (PID) controller. A PID controller uses a proportional term, an integral term, and
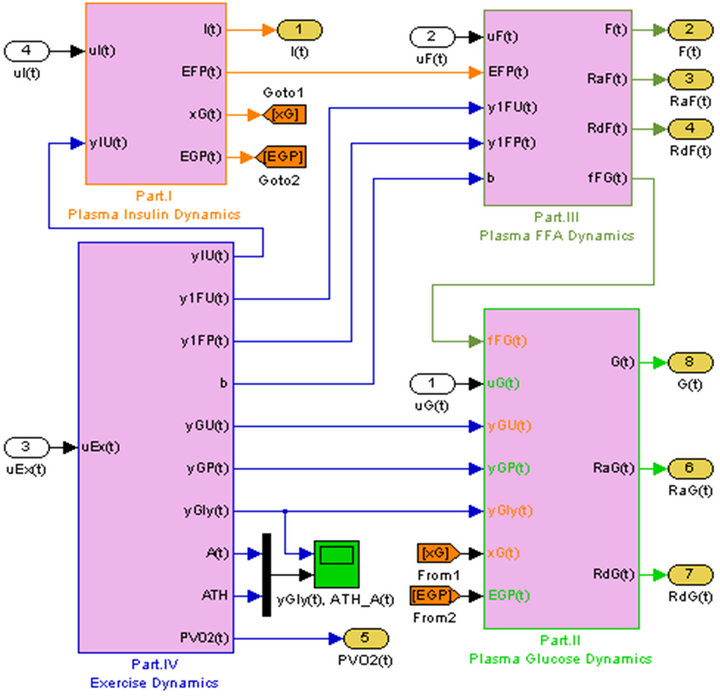
Figure 2. Simulation of the mathematical model of diabetic patient.
a derivative term, each with a coefficient that provides a weight for that term. In many processes in industry, PID controllers are used to keep some kind of a steady state [3,4].
The controller takes a measurement from a plant process and compares it with a setpoint (reference) value. The difference (or “error” signal) is then used to adjust the input to the plant in order to bring the measured value back to its desired setpoint. PID controller can adjust process outputs based on the history and rate of change of the error signal. The schematic diagram of the PID controller used with the composite model is shown in Figure 3.
3.2. Sliding Table Controller
This control algorithm translates BG levels readings into matching insulin delivery rates to be given to the patients. The basic sliding table has the form shown in Table 1, and features a commonly used starting scale for treating hyperglycaemia in critically ill patients at Sir Charles Gairdner Hospital, Perth, Western Australia [8].
Insulin delivery was adjusted at the turn of each sample time, and maintained at the new delivery rate during the sample. The control algorithm was configured to bring BG to the target range, taking a conservative control approach. Figure 4 shows the simulation model used for the sliding table controller.
4. Results of Controllers Tests
4.1. Single Mixed Meal Test
In this type of test we apply a single mixed meal and all
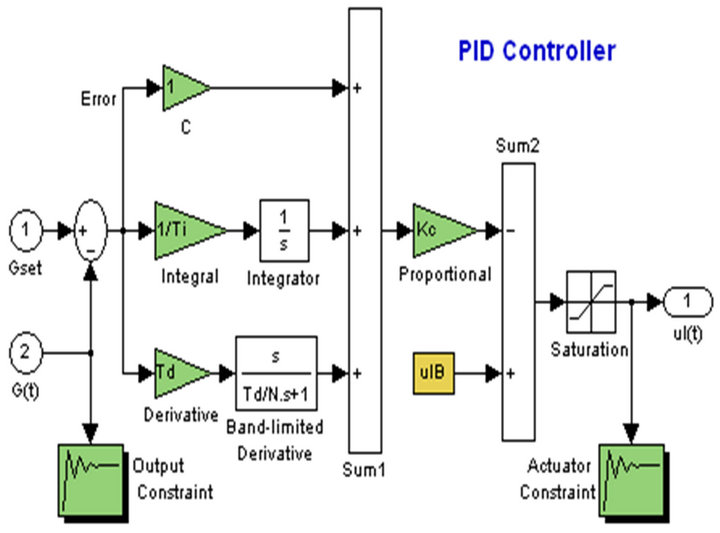
Figure 3. Simulation of the PID controller.
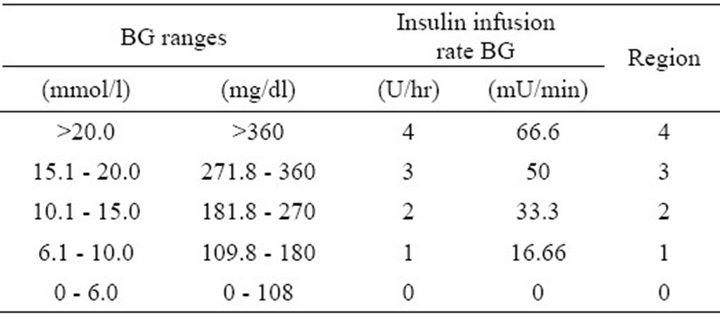
Table 1. Basic sliding table with a region assigned to each BG range.
controllers were adjusted to get best response to this test. The following table, Table 2 shows the single mixed meal contents used in the simulation.
Figure 5 shows the response of the plant to the single mixed meal with no controllers. In other words, there is no insulin infusion. Figure 6 shows the response of the plant to the single mixed meal when regulated by the PID method. On the other side, Figure 7 shows the response of the plant when controlled by the sliding table controller.
4.2. Daily Life Test
Here, we test how the controllers can deal with multi mixed meals and exercise, by supposing a daily life of a healthy person as shown in Table 3.
Although, the mixed meal for lunch and dinner have the same quantity, the blood glucose level has raised after dinner more than after lunch where both controllers has infused more insulin. However, the sliding table controller responded more clearer to blood glucose rise compared to the PID controller, as shown in Figures 8 and 9.
This result is due to the exercise that was done before the dinner time which caused the plasma FFA elevation. The increased availability of FFA at rest has an inhibitory effect on tissue glucose uptake, as shown in Figure
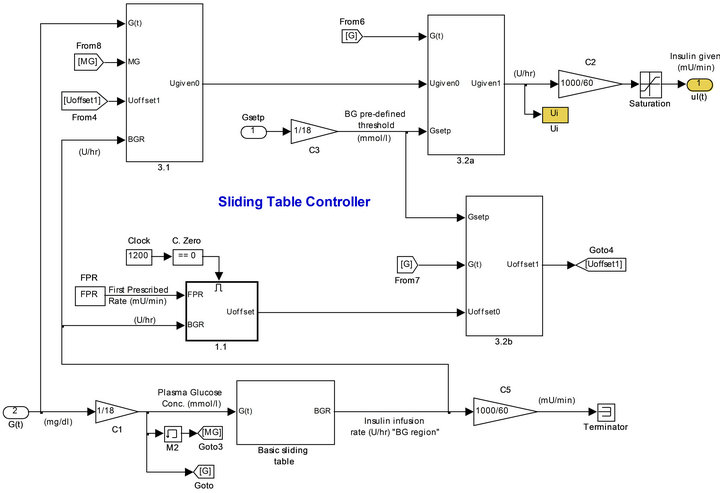
Figure 4. Simulation of the sliding table controller.

Table 2. Single mixed meal.
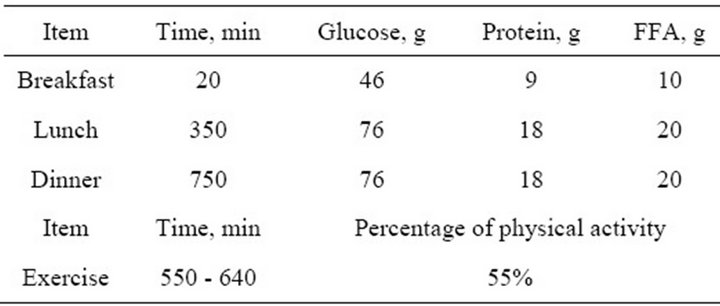
Table 3. Daily life of mixed meals and exercise.
10. Some important comparison results under daily life test between the PID and the sliding table controllers are given in Table 4.
4.3. Delay in Glucose Sensor Test
In this test, both controllers were tested against time delay in the glucose sensor (e.g. five minutes delay). The single mixed meal used in the simulation is as shown in the first test Table 2.
The response of the plant to the single mixed meal with time delay when controlled by the PID algorithm is shown in Figure 11. For a matter of comparison, the response of the plant when controlled by the sliding table controller is shown in Figure 12.

Figure 5. No control (no infused insulin) response of the plant to the single mixed meal.
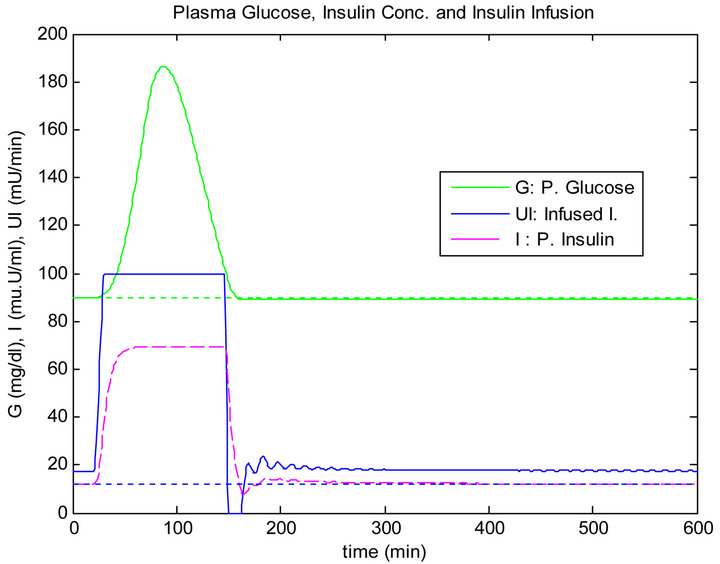
Figure 6. PID controller response to single mixed meal.
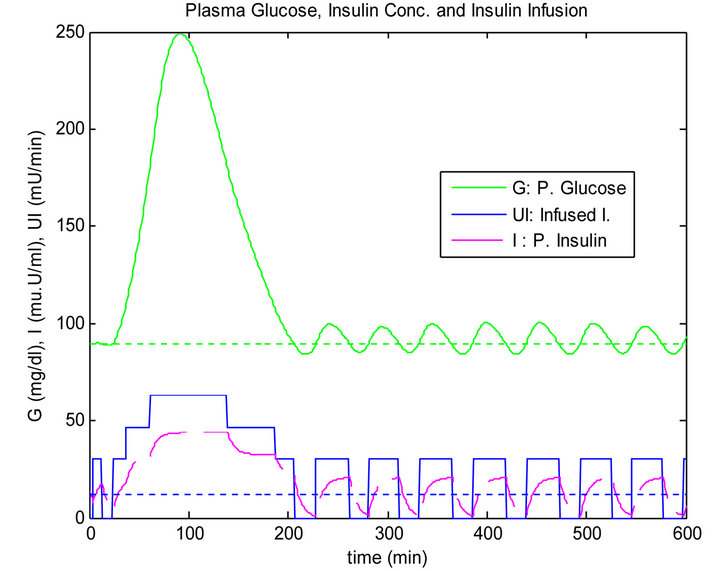
Figure 7. Sliding table controller response to single mixed meal.
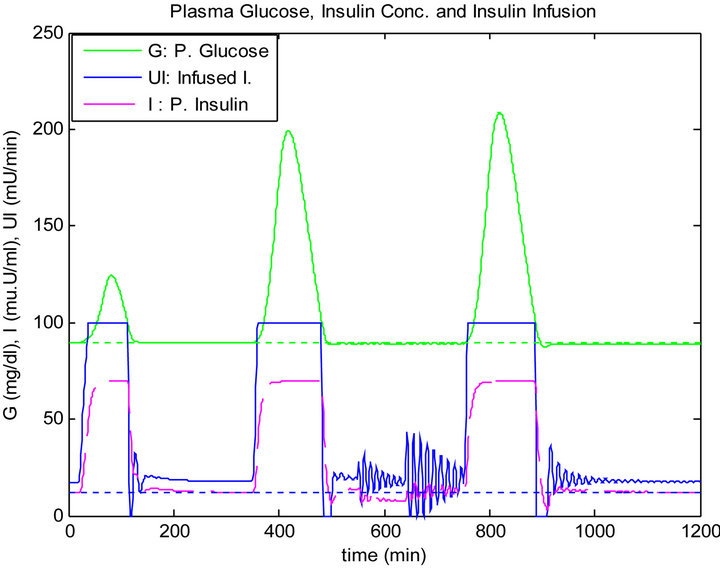
Figure 8. PID controller response to daily life test.

Figure 9. Sliding table controller response to daily life.
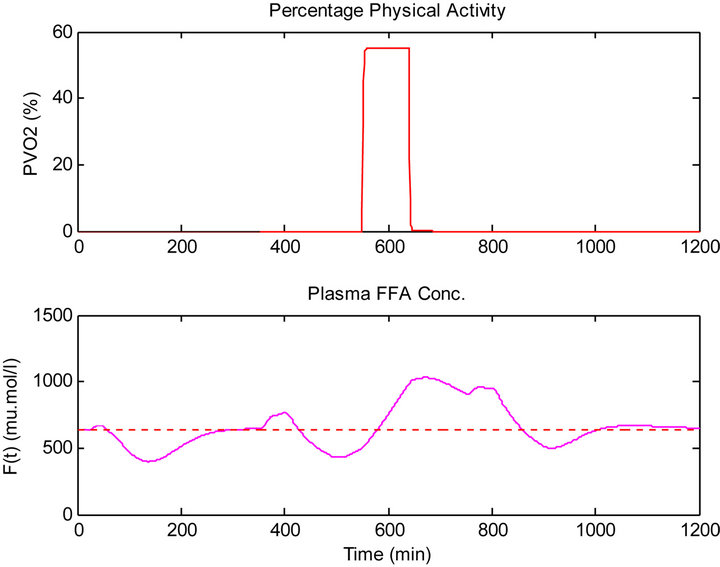
Figure 10. (Top) Percentage physical activity, (bottom) plasma FFA concentration.
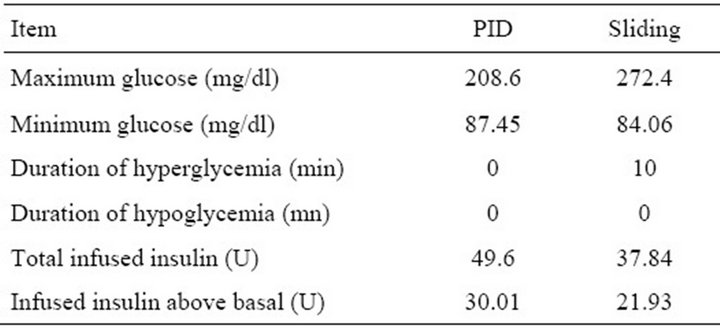
Table 4. Controllers measurement results of daily life test.
4.4. Noise in Glucose Sensor Test
In this type of test we apply a single mixed meal as shown in the last section, with signal to noise ratio (SNR = 10 dB) in the glucose sensor. The simulation results for both controllers are shown in Figures 13 and 14.
Table 5 illustrates comparative results using the PID and the sliding table controllers in response to different Tests on a single mixed meal, whereby, it is pretty obvious the total infused insulin, and the infused insulin above the basal line amounts are less using the sliding table controller.
5. Conclusions
The PID controller in daily life test has an ideal response where soon after the overshoot that happened due to the ingestion of mixed meal, the blood glucose BG level returned back to the basal level. In contrast, the overshoot in the Sliding controller is more than that what happened in the PID controller, where the effect of long time of high overshoot has a long term effect on the life of the patient.
In the stage of steady state, the sliding controller has an oscillation in blood glucose level. In the second test when the glucose sensor has 5 minutes time delay, the PID controller cannot keep the blood glucose level at the basal level. This drop in blood glucose level is below the basal line. It’s due to the wrong insulin doses causing danger to the patient, which has a short term effect on his/her life.
In contrast, the overshoot in the sliding controller is more than what happened in the PID controller; however, the sliding table controller has a less drop with almost constant oscillation around the steady state in blood glu-
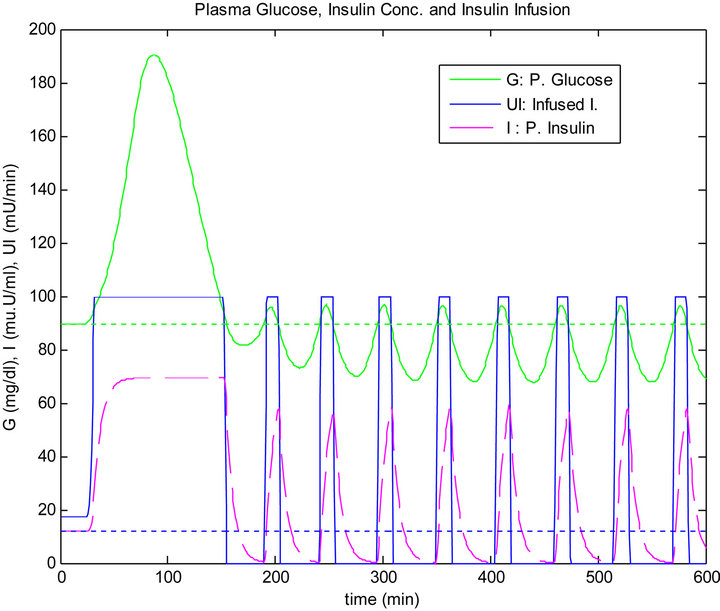
Figure 11. PID controller response to 5 min time delay.
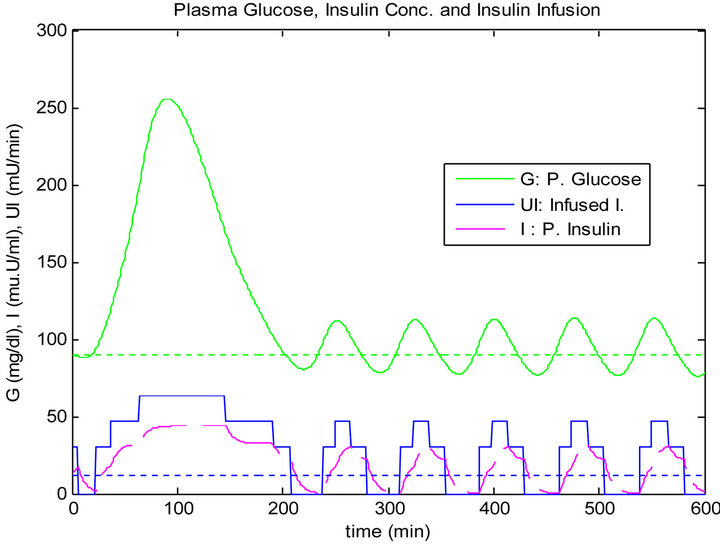
Figure 12. Sliding table controller response to 5 min time delay.
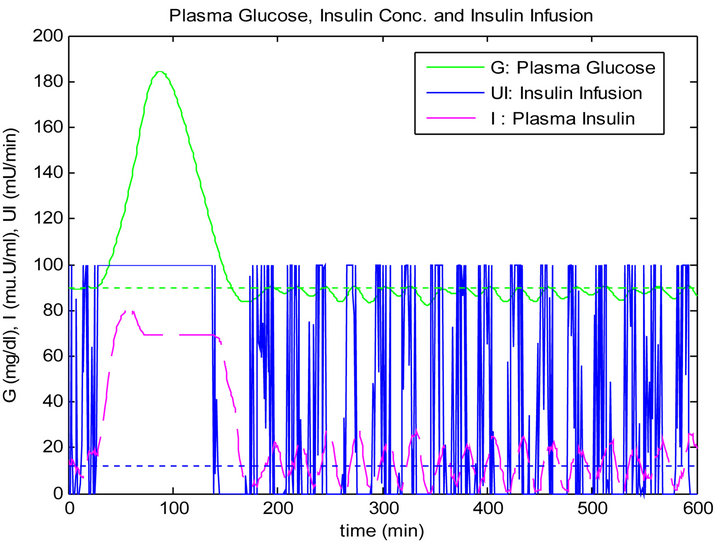
Figure 13. PID controller response to noise in glucose sensor.
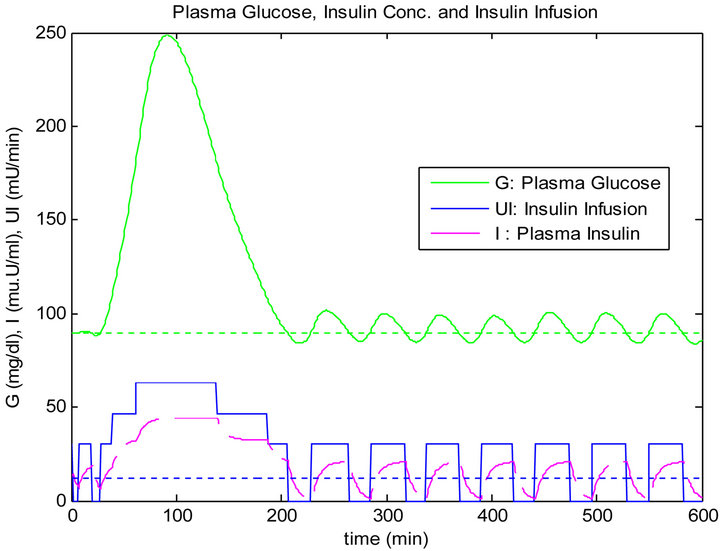
Figure 14. Sliding table controller response to noise in glucose sensor.

Table 5. Results of controllers response to different tests on single mixed meal.
cose level. Thus, less infused insulin is required.
In the third test when the glucose sensor has a 10 dB SNR, this caused a big confusion in the response of the PID controller and this is shown clearly in the stage of steady state before and after the time of ingesting the mixed meal. The response of the PID controller is not acceptable in the sense of control since the blood glucose level has an oscillation causing a big drop in blood glucose level below the basal.
In contrast, although the overshoot in the Sliding controller is more than that what happen in the PID controller, the controller has a stable oscillation in blood glucose level and less drop. Thereby, it’s requires less insulin infusion. In conclusion, taking into account all the previous testing circumstances, resulting tables and figures have shown that sliding table controller is more reliable, safer and less insulin consumption than the PID controller. Moreover, real world cases should have a delay or/ and noise in glucose sensor. Therefore, the sliding table control would be preferable and advisable when it comes to critical diabetes cases.
REFERENCES
- A. Roy, “Dynamic Modeling of Free Fatty Acid, Glucose, and Insulin during Rest and Exercise in Insulin Dependent Diabetes Mellitus Patients,” University of Pittsburgh, Pittsburgh, 2008.
- E. S. Berger, “Modelling Diabetes to Achieve ClosedLoop Control of Glucose Levels: A Literature Review,” Penn State Great Valley, School of Graduate Professional Studies, Malvern, 2007.
- J. Chen, K. Cao, Y. Sun, Y. Xiao and X. Su, “Continuous Drug Infusion for Diabetes Therapy: A Closed-Loop Control System Design,” Eurasip Journal on Wireless Communications and Networking, Vol. 2008, No. 44, 2008, Article ID: 495185.
- L. Kardar, A. Fallah, S. Gharibzadeh and F. Moztarzadeh, “Application of Fuzzy Logic Controller for Intensive Insulin Therapy in Type 1 Diabetic Mellitus Patients by Subcutaneous Route,” WSEAS Transactions on Systems and Control, Vol. 3, No. 9, 2008, pp. 712-721.
- E. D. Lehman and T. Deutsch, “The Physiological Model of Glucose-Insulin Interaction in T1DM,” Journal of Biomedical Engineering, Vol. 14, No. 3, 1992, pp. 235- 242. doi:10.1016/0141-5425(92)90058-S
- E. Berger, “Modeling Diabetes to Achieve Closed-Loop Control of Glucose Levels: A Literature Review,” Pennsylvania State University, Pennsylvania, 2007.
- E. Friis, “Modeling and Simulation of Glucose-Insulin Metabolism,” Technical University of Denmark, Kongens Lyngby, 2007.
- C. Frederick and F. Tyrone, “Closed-Loop Control of Blood Glucose,” Springer Verlag Berlin Heidelberg, Berlin, 2007.

