Intelligent Control and Automation
Vol. 3 No. 1 (2012) , Article ID: 17573 , 9 pages DOI:10.4236/ica.2012.31007
State Space Model Predictive Control of an Aerothermic Process with Actuators Constraints
1ASTIMI Laboratory, High School of Technology, Université Mohammed V Agdal, Rabat, Morocco
2UFR Automatic and Information Technologies, Faculty of Science, Rabat, Morocco
3Automatic Laboratory, Mohammadia School of Engineering, Rabat, Morocco
Email: musramzi@yahoo.fr
Received December 15, 2011; revised January 17, 2012; accepted January 25, 2012
Keywords: Multi-Variable Control; Aerothermic Process; Actuators Constraints; Process Identification; State Space Model Predictive Control
ABSTRACT
This paper investigates State Space Model Predictive Control (SSMPC) of an aerothermic process. It is a pilot scale heating and ventilation system equipped with a heater grid and a centrifugal blower, fully connected through a data acquisition system for real time control. The interaction between the process variables is shown to be challenging for single variable controllers, therefore multi-variable control is worth considering. A multi-variable state space model is obtained from on-line experimental data. The controller design is translated into a Quadratic Programming (QP) problem, in which a cost function subject to actuators linear inequality constraints is minimized. The outcome of the experimental results is that the main control objectives, such as set-point tracking and perturbations rejection under actuators constraints, are well achieved for both controlled variables simultaneously.
1. Introduction
The heating and ventilation system plays an important role in our daily life where certain desired temperature is controlled in order to maintain the healthy and safe working environment to the conditioned space. It is also the case in many industrial sectors including chemical, mineral, drying and distillation processes, as well as pharmaceutical and agroalimentary production units. It is argued that the temperature control is no more a challenging control problem in most of these applications. Nevertheless, some practical issues in many temperature control applications stimulate new developments and farther investigations [1-4].
For education and training purposes many aerothermic processes are available. They highlight most heating and ventilation problems, and they are widely referenced in process control literature. Different prototypes of these processes have been used to check new control strategies and many results were reported for the single variable control cases [5-9]. The aerothermic processes have generally a thermal protection for which they are entirely stopped when electrical power is maximal and the ventilator speed signal is under a given threshold.
In addition to these physical limits, there exists a significant interaction between the main processes variables which results from the nonlinearity of the process as reported in [8]. However, these constraints were not explicitly considered in most reported control approaches for aerothermic processes. Hence, the design of a multivariable feedback control system is worth to investigate. Among the many valuable approaches to face this kind of control problems, the Model Predictive Control (MPC) with constraints has been considered in this work. This choice is motivated by the fact that the MPC control has been investigated and successfully employed in some complex industrial processes [10-16].
In this paper, the State Space Model Predictive Control (SSMPC) with actuators constraints is considered for a pilot scale aerothermic process. To fulfil the requirement for integral action in most industrial control systems, we have embedded the SSMPC design model with integrators to achieve this objective and ensure outputs steadystate error free. This strategy is transformed into a Quadratic Programming (QP) problem, in which a quadratic cost function subject to linear inequality constraints is minimized on-line. The implementation of the predictive control in real time is based on the result of this minimization and only the first input of the optimal command sequence is used each time a new state is updated. In the synthesis of the SSMPC controller, a state space model is identified using the Numeric Subspace State Space System IDentification (N4SID). This technique has attracted an increasing attention of several researchers in the last few years [17-22]. It provides a robust and accurate method for the identification of dynamical systems under the influence of perturbations. Among the advantages of the N4SID method, we mention its ability to deal with multi-input multi-output identification in a straightforward manner from process experimental data and the ease of use due to the small number of parameters which have to be chosen by the user. This is a method that does not require nonlinear searches in the parameter space, but it is based only on computational tools such as the QR factorisation, and the singular-value decomposition (SVD), which make it robust and numerically stable [20]. The method contrasts with the robust design used in [1]. In this paper, we examine various issues of both N4SID identification and SSMPC control performances achieved experimentally on a pilot scale aerothermic process. The objectives of the proposed control technique which are about reaching reference set-points for the temperature and the air flow, subject to effects of both actuators constraints and the external perturbations. These goals are achieved by manoeuvring the heating resistance and the ventilator speed under constraints on the manipulated variables and their rate of change to handle the factory set thermal protection. Worth to mention herein that the basic factory control system delivered with the process is restricted to classical analog PID control, and most reported literature work on this kind of process deal with mainly mono-variable digital control. The results reported herein highlight further aspects of multivariable control of the considered process.
The paper content is organised as follows: Section 2 introduces the description of the aerothermic process and underlines the interaction between the main process variables. Section 3 discusses the multivariable state space identification, which is the first step in the design of the controller. Section 4 introduces the SSMPC algorithm where integral actions and set-point tracking are naturally embedded in the algorithm. In this section, we recall the main steps in the development of quadratic programming which implement the SSMPC. Section 5 reports the experimental control results of the aerothermic process operation under various inputs perturbations. Robustness of the SSMPC controller is also discussed and a final conclusion is given.
2. Aerothermic Process Description
The considered pilot scale aerothermic process [23], is shown as a schematic diagram in Figure 1 and depicted in a three dimensional view in Figure 2. As described in [24], it has the basic characteristics of a large process, with a tube through which atmospheric air is drawn by a centrifugal blower, and is heated as it passes over a heater grid before being released into the atmosphere.
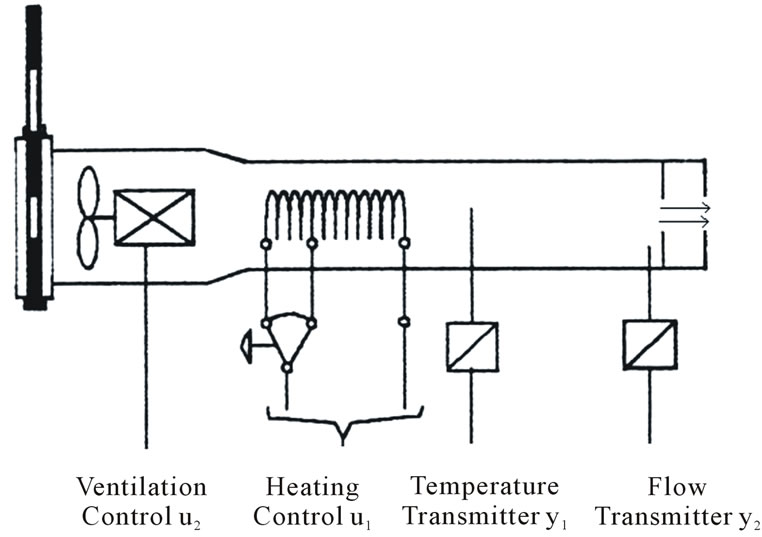
Figure 1. Schematic illustration of aerothermic process.

Figure 2. Three-dimensional view of aerothermic process.
The command objective for the aerothermic process is to regulate the temperature and the air flow by guaranteeing the verification of the full actuators constraints. The temperature control is achieved by varying the electrical power supplied to the heater grid. There is an energized electric resistance inside the tube, and due to the Joule effect, heat is released by the resistance and transmitted, by convection, to the circulating air, resulting in heated air. The air flow is adjusted by varying the speed of the fan.
This process can be characterized as a non-linear system. The physical principle which governs the behaviour of the aerothermic process is the balance of heat energy. Hence, when the air temperature and the flow inside the process are assumed to be uniform, a linear system model can be obtained.
As shown in the schematic of the aerothermic process, the system inputs, (u1, u2), are respectively the power electronic circuit feeding the heating resistance and the ventilator speed. The outputs, (y1, y2), are respectively the flow and air temperature. The input-output signals are expressed by a voltage, between 0 and 10 V, issued from the transducers and conditioning electronics.
To examine the possibility of interaction between the temperature and air flow of the aerothermic process, two experiments were carried out. In each case, the two process inputs were held constant and allowed to settle. If one of them undergoes a step change, the behaviour of the other output will be observed to see if this change had any effect on it. Figure 3 shows the results from both experiments. In the first half plot, the electric voltage supplied to the heater grid is held constant (at 4 V) and the speed of the fan undergoes a step change from 30% to 70% of its full range. The air temperature varied considerably from 4 V (45˚C) to 2 V (35˚C). The second half plot shows the results when the fan speed is held constant and the electric voltage of the heater grid undergoes a step change, from 40% to 80% of full range. As can be seen, the air temperature is varied accordingly but the air flow is remained unaffected. These results show that the air temperature behaviour depends also strongly on the operating conditions of the air flow.
3. State Space Identification
System identification is an experimental approach to determine the transfer function or equivalent mathematical description for the dynamic of an industrial process component by using a suitable input signal. This approach represents the first step in the design of a controller.
A considerable number of system identification methods have been investigated and they are generally classified into parametric approaches. In contrast to these classical algorithms, the State Space Method Identification (N4SID) does not suffer from the problems caused by a priori parameterizations and non-linear optimisations. They identify MIMO systems in a very simple and elegant way. Among his advantages we mention: these ability to deal with multi-input multi-output in a straightforward manner from process experimental data and the

Figure 3. Interaction between the aerothermic process main variables.
ease of use due to the small number of parameters which have to be chosen by the user. They are methods which do not require nonlinear searches in the parameter space, but it is based only on computational tools such as the QR and the singular-value decomposition (SVD), which make it robust and numerically stable [20].
In order to generate estimation and validation data for system identification, an experiment is performed. Data set used for the parameter identification step is build up with Pseudo Random Binary Sequence (PRBS) signals which are applied simultaneously to the two manipulated variables. This data set is displayed in Figure 4.
The sampling interval is Ts = 1 second. The signals collected, via the MF624 data acquisition module, are yield in the interval (0 V, 10 V). After the application of N4SID algorithm on first half experimental data of identification (i.e.: 100 minutes), the model of the aerothermic process is given by the following discrete state-space representation:
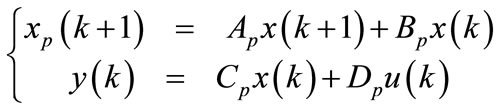 (1)
(1)
with



The matrix Dp is equal to zero, u = [u1, u2]T and y = [y1, y2]T.
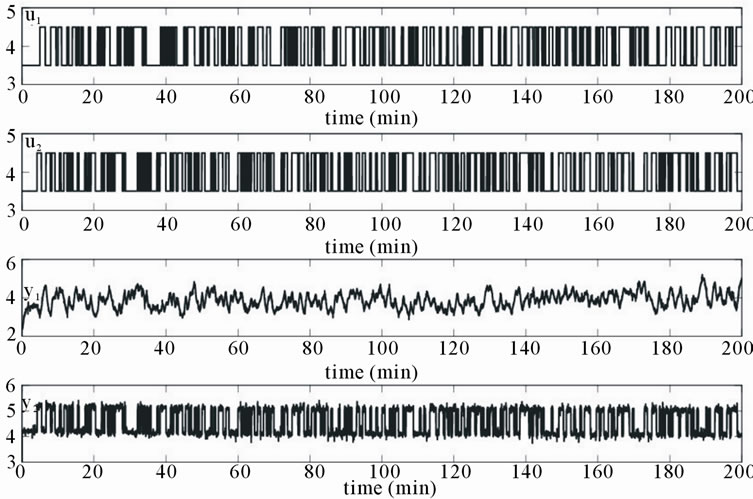
Figure 4. Data set for state space identification.
The system described by these matrices is stable, completely observable and controllable.
Once the model is identified, we have validated it by comparing his estimate output, when the input of the remaining experimental data is applied, with the true system output. This comparison is represented by the Figure 5.
As shown in this figure, it appears a good similarity between the true system output and the identified one.
4. Control Problem and SSMPC Formulation
The deterministic model of aerothermic process be controlled has two inputs, two outputs and four states. When the plant noise and perturbation are taken into consideration, the Equation (1) describing the aerothermic process becomes:
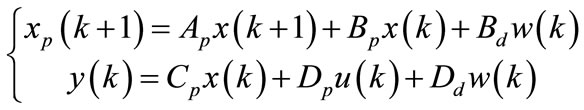 (2)
(2)
where xp(k) is the (4 × 1) state plant vector, u(k) is the (2 × 1) control input vector, y(k) is the (2 × 1) process output vector and w(k) is a (2 × 1) vector of perturbations. The matrices Du and Dd are assumed to be zero, this imply that there is not direct feed through of the manipulated variable and the perturbations on the output vector. Ap, Bp, Bd and Cp are matrices of appropriate dimensions. In order to ensure that integrators are embedded in the identified model, we need to change the model to suit this design purpose as in [10]. Taking a difference operation on both sides of the state equation in (2) yields:
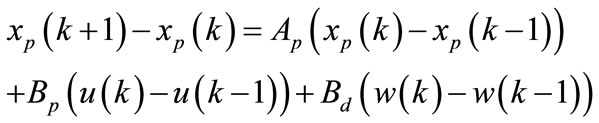 (3)
(3)
In general, the incremental of the variable v(k) is de-
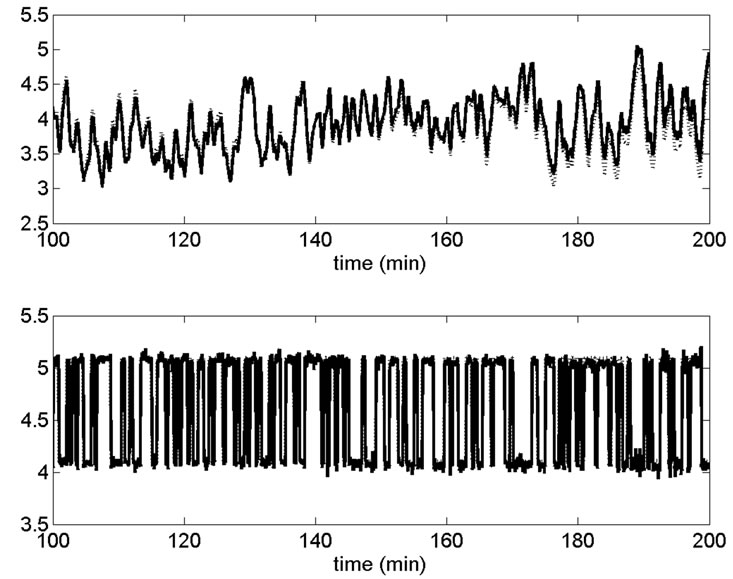
Figure 5. Outputs (solid line) and their estimates (dotted line).
noted by

With this information, the incremental state-space equation can be written as:
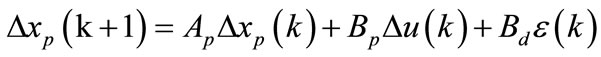 (4)
(4)
where Δu(k) is the input to the state-space model, also called the rate of change of the control inputs, and 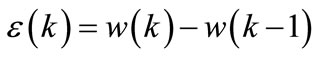 .
.
In order to relate the output y(k) to the state variable Δxp(k), a new state variable vector is chosen to be
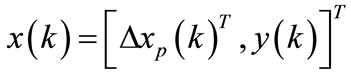
where superscript T indicates matrix transpose.
From (4) we deduce that
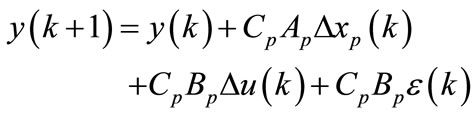 (5)
(5)
Putting together (4) and (5) leads to the following augmented state-space model:
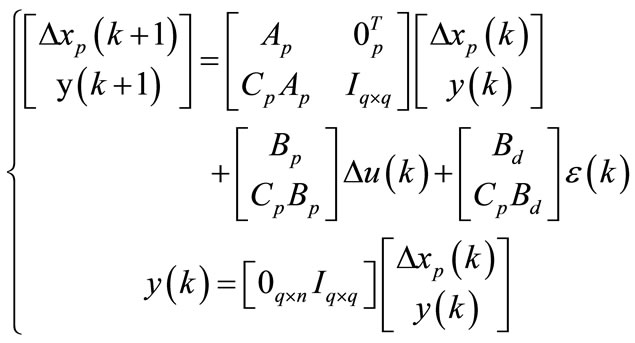 (6)
(6)
where the subscripts q and n are respectively the number of outputs and the state space model dimension. 0q×n is a q × n zero matrix and Iq×q the q × q identity matrix.
With the assumption that ε(k) is a zero-mean white noise sequence, the predicted value i samples ahead ε(k + i) is assumed to be zero.
For notational simplicity, we rewrite the augmented state-space model (6) as:
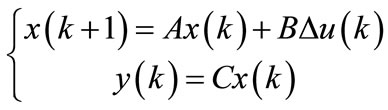 (7)
(7)
where A, B and C are matrices corresponding to (6). Their computation for the identified state space model of the considered aerothermic process yields the following results:
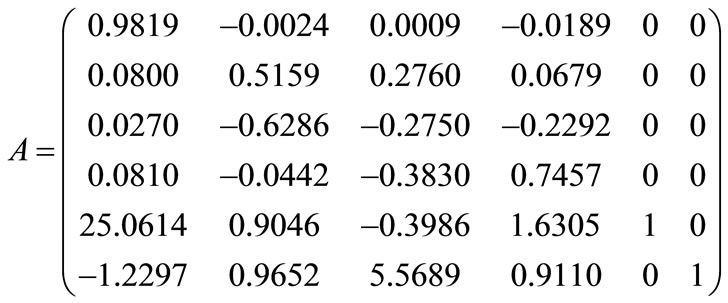
 ,
, 
The eigenvalues of the augmented model are given by:

The first two components of λ are from the augmentation of the state space model, and the last four are from the original plant. This means that there are 2 integrators embedded into the augmented design model, which ensures integral action for the SSMPC controller.
Define the vector Y and ΔU as
 (8)
(8)
where Np denotes the length of the prediction horizon or output horizon, and Nc denotes the length of the control horizon or input horizon.
Based on the state-space model (7), the future state variables are calculated sequentially using the set of future control parameters. After calculating the predicted output variables, we have the following compact matrix
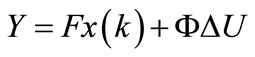 (9)
(9)
where
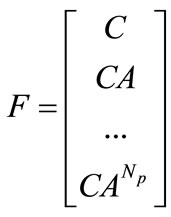
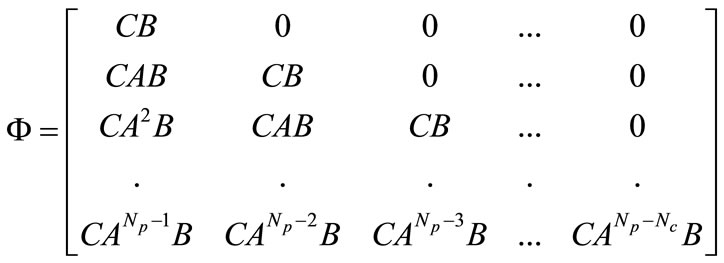
At time k, the state variable x(k) is not measurable (i.e.: C is different to the identity matrix). The control law is computed using the estimated state variables given by the following equation:
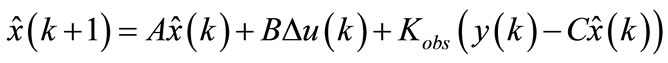
where Kobs is the Kalman filter gain Obtained by solving recursively (for i = 0, 1,···) the following equation:

where α and β are the matrices to be chosen by the user.
For a given set-point signal r(k) at sample time k, the main control objective is to bring the predicted output as close as possible to the set-point signal and annulled the effect of the perturbations with respect the actuators constraints. This objective is translated into a design to find the control parameter vector ΔU such that an error function between the set-point signal and the predictive output is minimized. The cost function J that reflects the control objective is defining as:
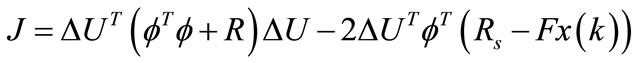 (10)
(10)
Subject to the inequality constraints
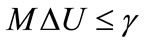
where M is a matrix reflecting the constraints and
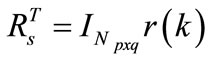
The matrix ΦTΦ has dimension mNc × mNc and ΦTF has dimension mNc × n and ΦTR equals the last q columns of ΦTF. The weight matrix R is a block matrix with m blocks and has its dimension equal to the dimension of ΦTΦ.
Since the cost function (10) is a quadratic, and the constraints are linear inequalities, the problem of funding an optimal predictive control becomes on of finding an optimal solution to standard Hildreth’s quadratic programming problem [10,11] and [25]. Hence, the problem is written as minimizing
 (11)
(11)
Subject to the inequality constraints
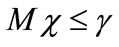 (12)
(12)
where
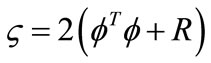 and
and 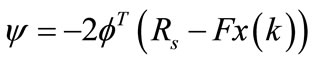
One the optimal solution to (11) at time k is obtained on line, its first element is applied to (1). The optimization (11) is repeated at time k + 1, based on the new state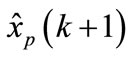 , yielding a moving horizon control strategy.
, yielding a moving horizon control strategy.
5. Experimental Results
The objectives of the control technique applied to aerothermic process are summarized below:
• The temperature and the air flow must reach given reference set-points.
• The actuators constraints must be verified and respected.
• The effect of the perturbations must be annulled.
• The effect of the interaction caused by the speed ventilator on the air temperature must be eliminated.
The predictive control setup described in the previous section was first tested in simulation using the model obtained from identification. This investigation was done especially to evaluate the computational complexity of the controller and to find the Nc and Np before the application of the controller in the real aerothermic process. Hence, we find Nc = 3 and Np = 20 and the weight matrix R = 0.5I6×6.
The implementation of the SSMPC, in real time, uses the Humusoft MF624 Data Acquisition Card of 14-bit Analog to Digital (A/D) conversion module, plugged into ISA port. The signals are transmitted between the PC and the Aerothermic Process via a 37-way cable and connector block.
In this experimental study, two types of echelon perturbations can be envisaged in order to challenge the control performances. The first one is characterized by the rotating of the diaphragm to 90 degrees. This perturbation affects the temperature and the air flow outputs. The second perturbation is characterized by the changing of the switch position (S) of the resistance heating. This perturbation affects the heater grid value, which increases the air temperature. The Figure 6 represents the aerothermic process controlled by the MIMO SSMPC technique. y, u, r and ω represent respectively the measured output or controlled variable, the manipulated input, the set-point and the perturbations. These vectors can be written as follows:

where w1 is the opening of the diaphragm and w2 is the heater grid level.
The constraints on the manipulated variables u(k) and their rate of change Δu(k) are taken into account to accommodate the system thermal protection for which the
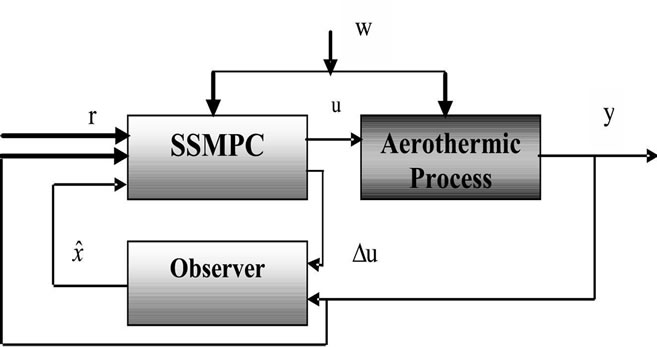
Figure 6. Block diagram of MIMO SSMPC application.
aerothermic process is entirely stopped when electrical power is maximal and the ventilator speed signal is under a threshold of about 1.25 V. Based on practical considerations of the process operation, these constraints may be summarized as follows:
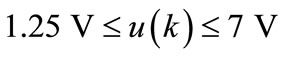 and
and 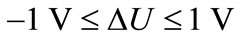
Furthermore the set of linear inequality constraints given by (12) is formulated into the following matrix form:
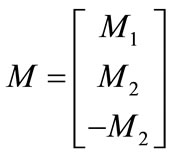 ,
, 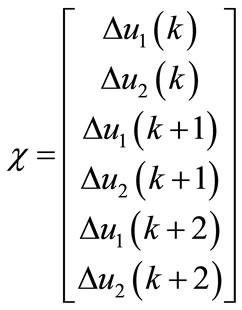

where I6×1 is a column vector of ones and I6×6 denotes the identity matrix, M1 = [I6×6, –I6×6]T,
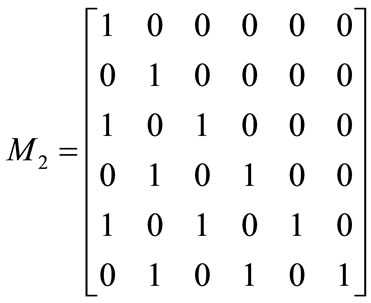
In our experimental application, the computation of Kobs gives the following result:

As shown in Figure 7, the set-points of the temperature and the air flow are changed respectively at 10 and 20 minutes. From this figure, it can be observed that both the temperature and the air flow reach their set-points imposed by respecting the operational full actuator constraints. The Figures 8 and 9 show the associated control signal responses and rates of change on both control signals respectively. The Figure 8 shows clearly the comportment of the control u1 at time 20 minutes in order to maintain the temperature at his desired set-point when
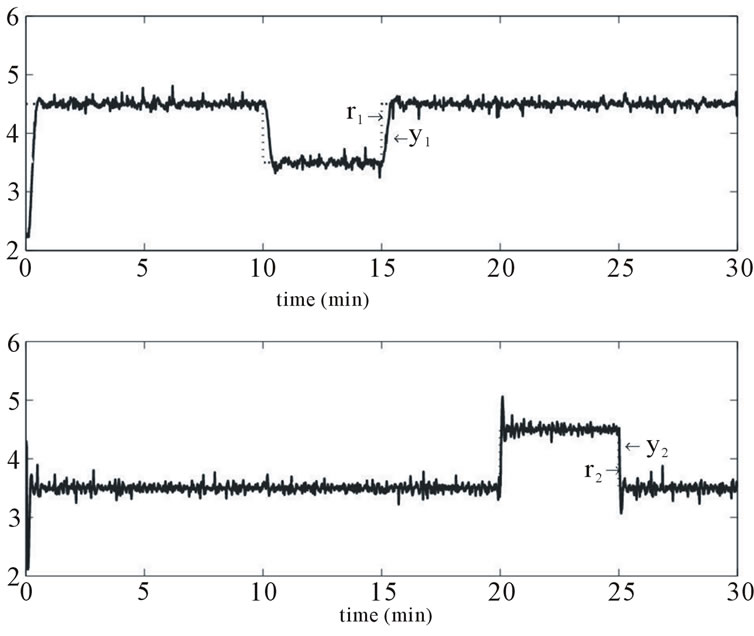
Figure 7. Closed-loop response: air temperature (top figure); air flow (bottom figure).
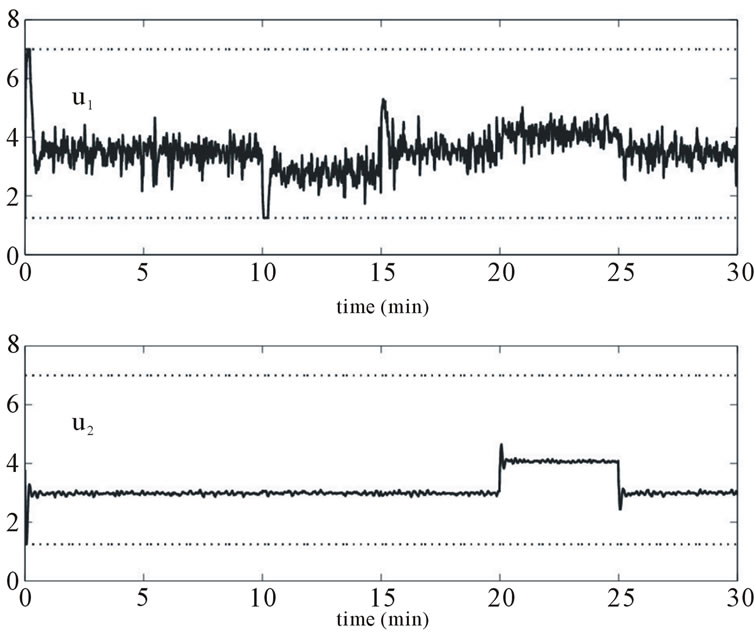
Figure 8. Closed-loop control signal response with actuator constraints. Top figure: heater grid (1.25 ≤ u1(k) ≤ 7); bottom figure: Ventilator speed (1.25 ≤ u2(k) ≤ 7).
the air flow reference has been changed. What means that the aerothermic process variables are coupled.
The Figure 10 shows the output responses when the perturbations are affected u1 and u2 respectively; while Figures 11 and 12 show the associated control signal responses and rates of change on both control signals respectively. As shown in the Figure 10, the perturbation on the air flow caused by opening of the diaphragm to 90 degrees, at time 31.75 minutes of the experience, is completely rejected. The perturbation on the air temperature, at time 42.8 minutes is also rejected. These rejections are due to the two integrators effect embedded in the SSMPC controller. The Figure 11 shows clearly the behaviour of the two command variables towards this rejection.
These experimental results show the efficiency of the
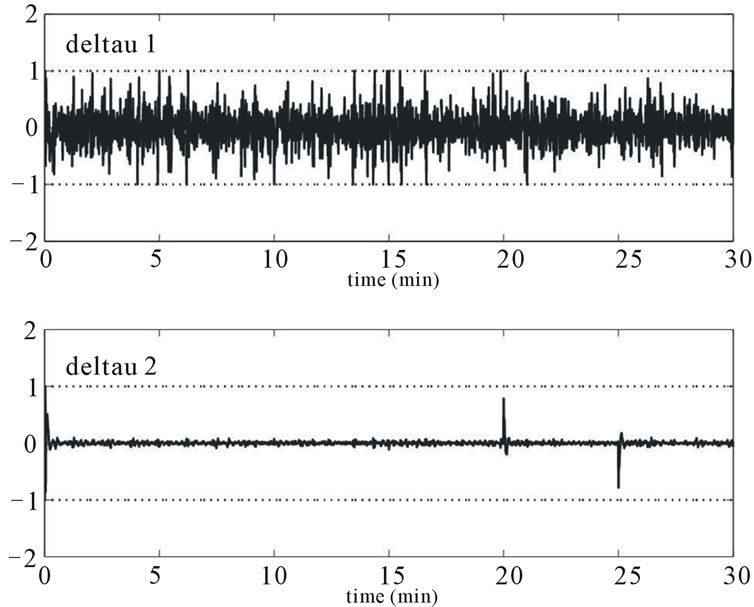
Figure 9. Rate of changes in control signal response. Top figure: rate of change for heater grid (–1 ≤ Δu1(k) ≤ 1); bottom figure: Rate of change for ventilator speed (–1 ≤ Δu2(k) ≤ 1).
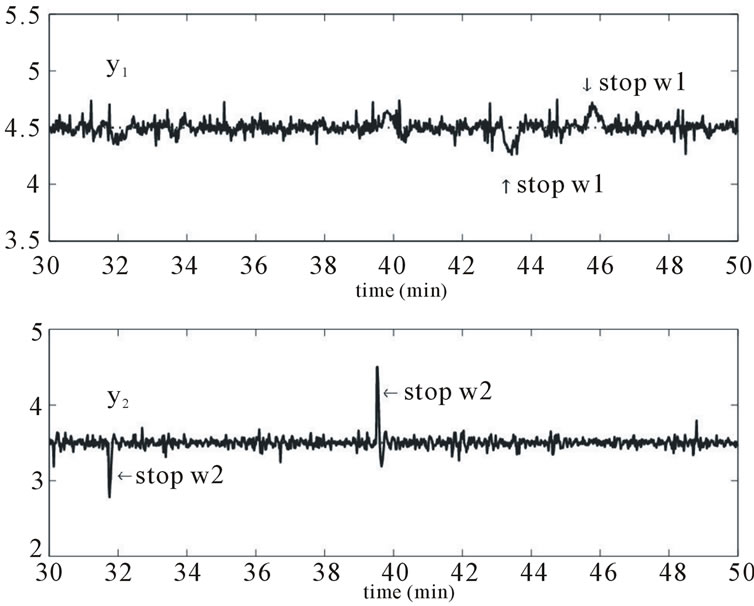
Figure 10. Closed loop response with perturbations. Top figure: air temperature; bottom figure: air flow.
SSMPC strategy, proposed in this paper, to control the temperature and air flow of the aerothermic process regardless the possible mismatch between the nonlinear process and his identified model. Furthermore, the SSMPC optimization problem has well taken into account the full actuators constraints compatible with the aerothermic process instruments. Noting that, the plant output constraints can be used. But, they are not required in this experimental application.
6. Conclusion
In this paper we have described a predictive control design approach with embedded integrators for a pilot scale aerothermic process. The number of these integrators is set equal to the number of outputs which make them
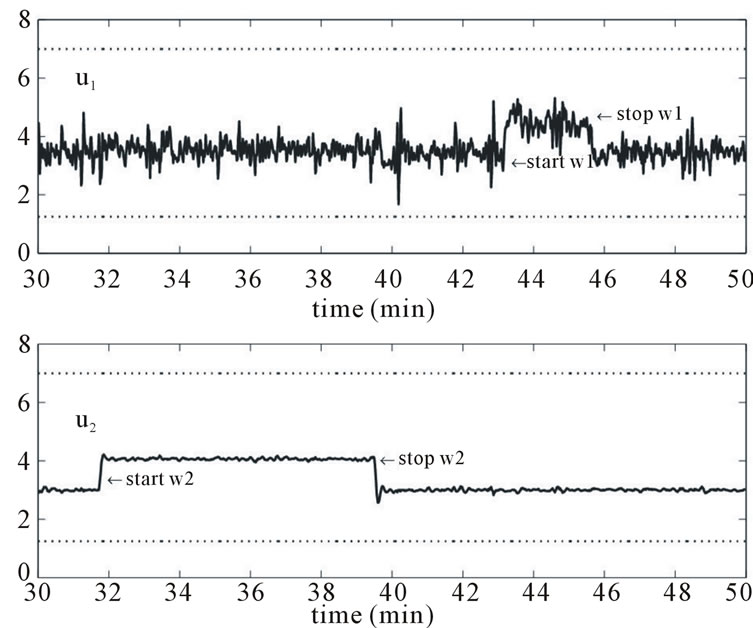
Figure 11. Closed loop control signal response with actuator constraints perturbations. Top figure: heater grid (1.25 ≤ u1(k) ≤ 7); bottom figure: Ventilator speed (1.25 ≤ u2(k) ≤ 7).
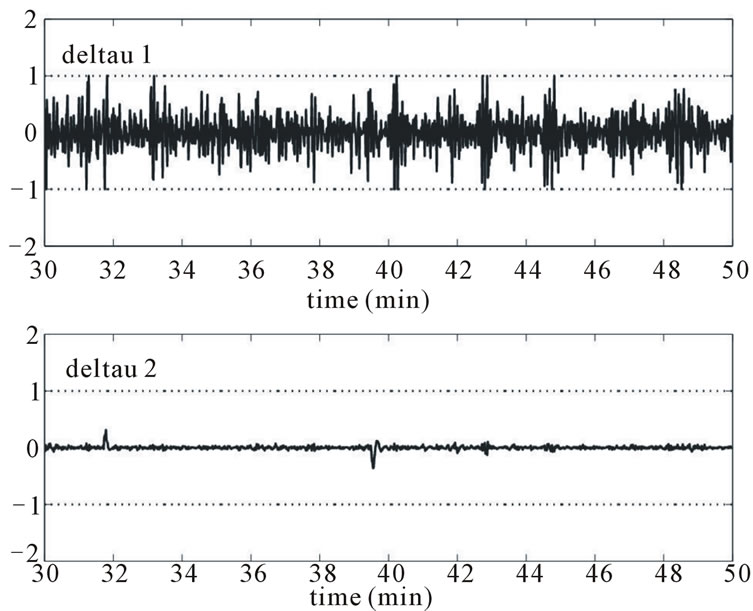
Figure 12. Rate of changes in control signal response. Top figure: rate of change for heater grid (–1 ≤ Δu1(k) ≤ 1); bottom figure: rate of change for ventilator speed (–1 ≤ Δu2(k) ≤ 1).
steady-state error free. The proposed control approach is versatile in that it allows embedding full actuators constraints. The SSMPC application results completely satisfy the requested specifications. The State Space Method Identification (N4SID) is used to identify the basic model of the SSMPC controller. An observer based on the Kalman filter is used to estimate the aerothermic process state variable. In conclusion, the use of MIMO SSMPC demonstrates robust performance for tracking set point changes and rejecting the perturbations without violating constraints. It constitutes a worth extension of the monovariable control methods and an alternative to the basic classical control for these kind of processes used for both engineering education and research training.
7. Acknowledgements
The authors would like to thank Professor Liuping Wang (School of Electrical and Computer Engineering, Royal Melbourne Institute of Technology (RMIT) University, Australia) for her very helpful remarks and suggestions to achieve this document.
REFERENCES
- N. Bennis, J. Duplaix, G. Enéa, M. Haloua and H. Youlal, “Greenhouse Climate Modelling and Robust Control,” Computers and Electronics in Agriculture, Vol. 61, No. 2, 2008, pp. 96-107. doi:10.1016/j.compag.2007.09.014
- M. Nachidi, F. Rodriguez, F. Tadeo and J. L. Guzmanb, “Takagi-Sugeno Control of Nocturnal Temperature in Greenhouses Using Air Heating,” ISA Transactions, Vol. 50, No. 2, 2011, pp. 315-320. doi:10.1016/j.isatra.2010.11.007
- R. F. Escobar, et al., “Sensor Fault Detection and Isolation via High-Gain Observers: Application to a DoublePipe Heat Exchanger,” ISA Transactions, Vol. 50, No. 3, 2011; pp. 480-486. doi:10.1016/j.isatra.2011.03.002
- M. F. Rahmat, N. A. Mohd Subha, K. M. Ishaq and N. Abdul Wahab, “Modeling and Controller Design for the VVS-400 Pilot Scale Heating and Ventillation System,” International Journal on Smart Sensing and Intelligent Systems, Vol. 2, No. 4, 2009, pp. 579-601.
- H. L. Ho, A. B. Rad, C. C. Chan and Y. K. Wong, “Comparative Studies of Three Adaptive Controllers,” ISA Transactions, Vol. 38, No. 1, 1999, pp. 43-53. doi:10.1016/S0019-0578(99)00004-X
- T. Kealy and A. O’Dwyer, “Closed Loop Identification of a First Order plus Dead Time Process Model under PI Control,” Proceedings of the Irish Signals and Systems Conference, University College, Cork, 25-26 June 2002, pp. 9-14.
- D. M. de la Pena, D. R. Ramirez, E. F. Camacho and T. Alamo, “Application of an Explicit Min-Max MPC to a Scaled Laboratory Process,” Control Engineering Practice, Vol. 13, No. 12, 2005, pp. 1463-1471. doi:10.1016/j.conengprac.2004.12.008
- R. Mooney and A. O’Dwyer, “A Case Study in Modeling and Process Control: The Control of a Pilot Scale Heating and Ventilation System,” Proceedings of the 23rd International Manufacturing Conference, University of Ulster, Jordanstown, August 2006, pp. 123-130.
- N. A. M. Subha, M. F. Rahmat and K. M. Ishaq, “Controller Design for a Pilot-Scale Heating and Ventilation System Using Fuzzy Logic Approach,” Jurnal Teknologi Keluaran Khas, Vol. 54, 2011, pp. 123-139.
- L. P. Wang, “Model Predictive Control System Design and Implementation Using MATLAB,” Springer, Berlin, 2009.
- L. Wang and P. C. Young, “An Improved Structure for Model Predictive Control Using Non-Minimal State Space Realisation,” Journal of Process Control, Vol. 16, No. 4, 2006, pp. 355-371. doi:10.1016/j.jprocont.2005.06.016
- J. M. Maciejowski, “Predictive Control with Constraints,” Prentice Hall, Upper Saddle River, 2002.
- A. Bemporad, F. Borrelli and M. Morari, “Model Predictive Control Based on Linear Programming the Explicit Solution,” IEEE Transactions on Automatic Control, Vol. 47, No. 12, 2002, pp. 1974-1985. doi:10.1109/TAC.2002.805688
- J. H. Lee and B. L. Cooley, “Min-Max Predictive Control Techniques for a Linear State-Space System with a Bounded Set of Input Matrices,” Automatica, Vol. 36, No. 3, 2000, pp. 463-473. doi:10.1016/S0005-1098(99)00178-8
- S. J. Qin, V. M. Martinez and B. A. Foss, “An Interpolating Model Predictive Control Strategy with Application to a Waste Treatment Plant,” Computers and Chemical Engineering, Vol. 21, No. 1, 1997, pp. S881-S886. doi:10.1016/S0098-1354(97)00160-9
- T. Kawabe, “Robust MPC Method for BMI Based Wheelchair,” Intelligent Control and Automation, Vol. 2, No. 2, 2011, pp. 340-350. doi:10.4236/ica.2011.24039
- P. V. Overschee and B. D. Moor, “N4sid: Subspace Algorithms for the Identification of Combined Deterministic-Stochastic Systems,” Automatica, Vol. 30, No. 1, 1994, pp. 75-93. doi:10.1016/0005-1098(94)90230-5
- M. Verhagen, “Identification of the Deterministic Part of Mimo State Space Models Given in Innovations form from Input-Output Data,” Automatica, Vol. 30, No. 1, 1994, pp. 61-74. doi:10.1016/0005-1098(94)90229-1
- S. J. Qina, W. Lina and L. Ljung, “A Novel Subspace Identification Approach with Enforced Causal Models,” Automatica, Vol. 41, No. 12, 2005, pp. 2043-2053. doi:10.1016/j.automatica.2005.06.010
- M. Viberg, “Subspace-Based Methods for the Identification of Linear Time-Invariant Systems,” Automatica, Vol. 31, No. 12, 1995, pp. 1835-1852. doi:10.1016/0005-1098(95)00107-5
- M. Lovera, T. Gustafsson and M. Verhagen, “Recursive Subspace Identification of Linear and Nonlinear Wiener State Space Models,” Automatica, Vol. 36, No. 11, 2000, pp. 1639-1650. doi:10.1016/S0005-1098(00)00103-5
- T. C. S. Wibowo and N. Saad, “MIMO Model of an Interacting Series Process for Robust MPC via System Identification,” ISA Transactions, Vol. 49, No. 3, 2010, pp. 335-347. doi:10.1016/j.isatra.2010.02.005
- http://www.didalab-didactique.fr/2008/achat/produit_details.php?id=32&lng=FR
- E. Yesil, M. Guzelkaya, I. Eksin and O. A. Tekin, “Online Tuning of Set-Point Regulator with a Blending Mechanism Using PI Controller,” Turkish Journal of Electrical Engineering, Vol. 16, No. 2, 2008.
- P. J. Gawthrop and L. Wang, “Intermittent Predictive Control of an Inverted Pendulum,” Control Engineering Practice, Vol. 14, No. 11, 2006, pp. 1347-1356. doi:10.1016/j.conengprac.2005.09.002

