Received 2 January 2015; accepted 19 January 2015; published 22 January 2015

ABSTRACT

Due to the rapid growth of online transactions on the Internet, authentication, non-repudiation and integrity are very essential security requirements for a secure transaction. To achieve these security goals, digital signature is the most efficient cryptographic primitive. Many authors have proposed this scheme and prove their security and evaluate the efficiency. In our paper, we present comprehensive study of conventional digital signature schemes based on RSA, DSA and ECDSA (Elliptic Curve Digital Signature Algorithm) and the improved version of these scheme.

Keywords:

Digital Signature, RSA, DSA, ECDSA, Security

1. Introduction

Nowadays all important works and transactions come in various electronic mechanism forms such as E-com- merce, E-government, E-shopping, E-mails, E-learning etc. All these E-services need to establish an electronic framework that achieves the security, confidentiality, authenticity, integrity and non-repudiation of the sensitive information is being moved among deferent parties; because the success of these services is entirely dependent on security. The most important solution to address these critical challenges is digital signature. All information transmitted must be first signed by its original sender digitally. In our professional lives, the person might reject which he implemented signature in a instrument of a session, but to reject a digital signature is impossible be- cause making that is to principally evidence which the security for private key is jeopardized before establishing for digital signature. Thus, the matter of fact which creation for digital signature might need secure private key, while the symmetric public key is applied to declare the signature. Thus, non repudiation is basic characteristic for digital signature. There are some correcting schemes, like digital signature, that might link simultaneously the identity for an organization or system to person with the private key and the public key, so hard of individual rejects of digital signature. Thus, the digital signature will respond for the following necessities [1] :

− The receiver might check the signature for transmitter. However he could not change.

− While the transmitter transmits the signature message to the receiver, he can not reject of the transmit message.

− While the transmitter or receiver had contention about the content and source of message, they might offer the tightener to proof which the transmitter has set that the signature of the message which previously been transmit.

But digital signature is various on signatures that written by hand. The handwritten signature is similar and also differs from one individual to another one. Thus, simulation be potential, no attention for any language is applied. In computer science, digital signature is a chain composition, from digits that are 0 and 1, which differs through the message and is impossible to simulate. Digital signatures are being used to achieve integrity, non-repudiation and authentication of the digital data in transmission among different end users. Digital signature offers suitable architecture for sending secure messages by using different algorithms. The digital signature algorithms generally are consisting of three sub phases:

1) Key generation symmetric or asymmetric algorithm.

2) Signing algorithm.

3) Signature verification algorithm [1] .

The symmetric key algorithm generates single key that is shared by sender and receiver. On other hand, the asymmetric key algorithm generates two keys: public and private keys. The public keys are shared between two parties; in contrast the private keys are keeping secret. During second phase signing algorithm the digital signa- ture is generated by taken plain text i.e. private key, sensitive data, and message as input. After that, the sender sends the message along with generated signature to the intended recipient. Signature verification algorithm is executed at recipient end to ensure the received data [1] . A valid digital signature gives a receiver the reason to accept message and ensure the message was created and transmitted by a known sender, not altered in transit. Digital signature has many schemes, such as RSA, DSA and ECDSA, which are used to impose the security of different transaction. Table 1 summarizes the key strength of ECDSA and RSA/DSA. It is clear that ECDSA has much smaller key strength [2] . Thus ECDSA is the scheme that is quite popular of late. In our paper, we will seek to provide a comprehensive survey of the original digital signature schemes. And also this survey includes the recently improved digital signature schemes, which present improvement that is achieved on each scheme. Then it will explore the similarity and difference between improved schemes and original schemes. As shown in Figure 1, a taxonomy graph of approach classifies our survey. Digital signature schemes were improved in

order to overcome some of vulnerabilities. We review some of the improvement techniques of digital signature schemes that achieved with respect to various perspectives. In RSA, it is fault tolerance perspective, while in DSA, they are speed of operation computational perspective and longtime of computations perspective. And in ECDSA, they are efficiency perspective and speed of operation computational perspective.

2. Organization of the Article

This paper is organized as: section II briefs about digital signature schemes, Section III presents a comparison between improved schemes and original schemes and section IV shows the unresolved problems and further re- search.

3. Background

3.1. Conventional Digital Signature Scheme-RSA

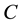The RSA (short of Rivest Shamir Adleman) used modulo concept in arithmetic for perform signature of a message digitally [2] . It provides message recovery. The RSA public-key encryption scheme the message and the cipher text. Key Generation process in RSA public key cryptosystems are as:

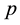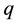− Both sender and Receiver create primes and that are two large distinguished random numbers.

− Computes 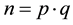and.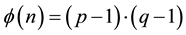

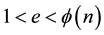− Selects a integer number is random such that, where.

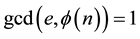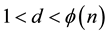− Computes integer is unique such that, where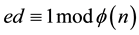. Thus, sender has the public key is 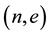and private key is.

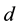− Signature Generation process are as the following:

Ÿ A message, Sender defines with a number through a map.

Ÿ Sender computes the signature.

− Verification process of Alice Signature is as the following:

Ÿ Bob chooses the public key of Alice.

Ÿ Bob computes.

Ÿ Bob verifies that where denotes the set of images of. The signature rejects, if does not hold else recovers the message as.

3.2. DSA Signature Scheme

DSA(short of Digital signature algorithm) that use different domain parameters such as is the private key, is per message secret key number, signed the data, and the hash function [2] . Digital signature algorithm checked by that is the public key, checked the data and also the same hash function that used through creating of signature. So, the parameters implemented are as following:

− A prime modulus is.

− A prime divisor for is.

− A generator for the sub group for order is.

− The private key that is a randomly integer elected in the range is.

− The public-key is. It acquired by.

− Message has is secret key.

The message has the signature consists of both numbers and implemented by using:

− .

− bits for Hash.

− ; is the signature created.

Alice transmits message, and the signature to Bob. To verify of the signature, Bob implements the following steps: He will verify which and; the signature will reject; if any one of the condition violated. If two the conditions are not violated in the first phase, Bob calculates

−

− is the farthest to the left bits for

−

−

−

If, the signature is accepted.

3.3. Conventional Digital Signature Scheme-ECDSA

Elliptic Curve Digital Signature Algorithm(ECDSA) is the version for elliptic curve cryptographic for digital signature algorithm [1] . There are fixed group of Elliptic Curve EC domain that contain these parameters

that associated of the key pair of Alice, where: A prime is. The Field Representation is.

− Parameter generation: The two field elements in are and. consist of and that are two field elements and a limited point for prime arrangement in which is elliptic curve defined over. is the cofactor. To create the key, Alice makes following the steps:

Ÿ Selects integer is a random within the interval.

Ÿ Computes.

Ÿ Public key of Alice is and private key is.

− Signature generation: For perform signature of a message are the following.

Ÿ By domain parameters. Alice selects a pseudo random or random integer within the interval.

Ÿ She Computes and such that is an integer number between 0 and. If equal 0 subsequently again return to the first step.

Ÿ Computes.

Ÿ Computes, such that is Secure Hash Algorithm (SHA-1). If equal 0, subsequently again return to the first step.

Thus, the signature of the message is the both of integers.

− Signature Verification: For verify of Alice’s signature on message, Bob will obtain certified version for Alice’s parameters of domain and public key. Bob verifies as the following:

Ÿ Check which two integers and are within the interval.

Ÿ Calculates and

Ÿ Calculates and.

Ÿ Calculates and.

The message signature is valid if equal, else stated invalid by Bob.

4. Improved Digital Signature Schemes

4.1. Improved Schemes of RSA

We describe two improved schemes for original RSA which can maintain the fault tolerance function. These schemes provide security requested when data transmitted over network.

Fault Tolerance Perspective: There are a security vulnerability in Lin et al.’s scheme [3] . A malicious user can easy forge the message through the use of valid signature of the original message. Of easy to malicious user creates forge a message through the use of valid signature of the original message. In order to overcome this problem, was improved this scheme in [5] . The proposed scheme provide requirements of digital signatures. And contains the function of fault tolerance. Also, it can be used in cloud computing.

In proposed scheme, the major method is to provide two matrix of the prime numbers. In order to overcoming a security vulnerability. While a somebody intercepts matrix of message which transferred then try to permu- tation columns and rows in the matrix. In order establish a new message where has same signature.

(1)

Since

(2)

where is permuted by row and is permuted by column. Malicious users cannot creates a valid message. Where carries same signature , by permutation in the matrix [6] presents an improved scheme contains digital signature, encryption and function of fault tolerance. Scheme adopted on the permutation matrix. Thus, must attacker to resolve problem of the homogeneous. The scheme have good security. Moreover, it allows the recipient to check identity of the sender. It has safer encrypting way. Attacker must to solve the problem of a graph symmetry. And it computational processes can’t completed. The improved scheme has a slow speed. And it has reliable with respect to in the tight security progress against any CCA2 attack.

4.2. Improved Schemes of DSA

In the next section, we offer some improved schemes based on traditional DSA. The researchers modified of this scheme from two perspectives which are speed of operation computational perspective and a long time of computations perspective. On Speed of Operation Computational Perspective, the security of big data the environment demanded and especially, with the sharp increment of data capacity. So, necessity utilization various security technologies are demanded to achieve more speed. The researchers in [7] proposed an improved speed algorithm called as is DSA that improves the computing speed of DSA. This algorithm modifies original DSA structure and avoids complex and time-consuming modular inverse operation in the signature and the verification processes. Is DSA requires only simple arithmetic in the signature process which are one subtraction, one multiplication, one modular operation and one Hash. There isn’t any pre computation in verification process of is DSA. They performed simulation of is DSA and DSA on the complex operations on lager numbers include a large prime generation, modular exponentiation and modular inverse. They are setting the length of modulus 1024-bits. Thus, the simulation testing result showed that the signature speed of is DSA and DSA with pre- computation were same and very fast because of no complicated and time-consuming modular inverse and modular exponentiation. When the testing accuracy is ms, both of the signature speeds are presented as 0. In the verification of is DSA and DSA, are required to calculate twice modular exponentiation operations, but there is once modular inverse in DSA contrast with no modular inverse in is DSA. Thus, the verification speed of is DSA is increased by 25.40 than DSA because without the pre-computation condition. The researchers compared and analyzed the security of is DSA and DSA and the equations presented to compute the private key and launch forgery attacks. The result analysis proved that is DSA has the same security strength with DSA which is the difficulty of solving the discrete logarithm.

On long Time of Computations Perspective, it is known in advance, traditional DSA algorithm requires a new unique and random integer for each signing. The must be secret and chosen by user for every message to be signed. In [8] the author proposes a new signature schemes based on the contumacy search problem. The security of this proposed scheme is totally depends on difficulty of the conjugacy search problem. In this scheme all chosen parameters for signing message and verifying signature such as public keys and integer are belong to Miller group and the security of this scheme is absolutely increasing by difficulty CSP in. A major difference between DSA and this proposed scheme is that the proposed scheme cannot change for every new signature. So, pre computations of could be done long before Bob is present.

4.3. Improved Schemes of ECDSA

ECC is a methodology of public-key cryptography that based on algebraic structure. An ECC scheme helps in obtaining the wanted security level with smaller keys than that of the corresponding RSA schemes. Speed and efficient use of power, and storage are some of the important merits of utilizing smaller keys. Next we will review some enhancement techniques of ECDSA.

− Efficiency Perspective: ECDSA became a standard and will be used in information security system. But it could not be used in the devices that have limited compute and storage capacity such as ATM, smart card and PDA. In [10] proposed two schemes cost efficiency while keeping the same security level as compared to ECDSA. The first scheme is suitable for these devices at the signer side. The operation amount of signa- ture can be reduced to. The second scheme is suitable at the verifier side but the operation amount of signature will be the same as ECDSA. The advantage of using this scheme is it reduces the computational cost at the signer but the second scheme could not be used to reduce the operation amount of signature verification.

− Speed of Operation Computational Perspective: The key factor to the overall performance of ECDSA is the optimization of scalar multiplication because it is time consuming process. [11] propose a novel scalar generation algorithm by extending an integers periodically. Then apply the proposed algorithm in ECDSA by generating random scalar in ECDSA [14] . The proposed algorithm Contribution is it can speed up the computing of elliptic curve scalar multiplication. The advantages of using this algorithm are the count of the point addition of the proposed scalar is reduced dramatically without extra memory, has small growth rate with the bit length of scalar and suitable for hardware implementation. ESDSA performance de- pends on a point multiplication operation. The root cause of security fall of ECDSA is that it shares three points of the elliptic curve publicly which makes it possible for an adversary to measure the private key of the signer. [12] proposed new ECDSA that generates point to calculate the private key and a random number to calculate the public key. Through using generating point as private key, signer provides two points to adversary unlike the original ECDSA that provides three points. Also the value of random number, which used for signature generation, can never be computed because the generating point is not available publicly. The proposed ECDSA consists of less number of point-addition, point multiplication and point doubling processes which improves the execution speed of the algorithm and the security [9] [13] . The advantages of using this scheme are less complex process, it provides more security, and less number of curve points provided publicly, reduces number of point multiplication in signature verification process, reduced point addition operation in signature verification process, reduces number of parameters made public and remove the overhead to calculating.

5. Comparative Study

In this survey, we have presented a comparison between the improved digital signatures schemes and original conventional schemes as shown in Table 2.

Computational Cost

In this section, we presents the computational costs for key generation, signing and verification. Table 3 and Table 4 summarize fastest result for each operation and the performance of each from the operations on

signature generation and verification.

6. Legal Implications

The following signature schemes are suitable if they meet the requirements of key lengths and parameter values, which were suitable for the creation of qualified electronic signatures and qualified certificates. Table 5 and Table 6 summarize the suitable key lengths for each scheme up to the end of 2019 [4] [9] .

7. Further Research on Unsolved Problems

We have explored some unresolved problems and difficulties in different digital signature schemes that are considered as good new research opportunities. There are some aspects for future works, the idea to optimize and enhance security level and increase performance for different schemes [4] [9] . In addition, analyzing and comparing the performance each from schemes in different systems and developing of digital signature when use in cloud computing field. There are many from unresolved problems and difficulties that discovered in different digital signature schemes described as the following:

− In order running, the RSA algorithm requires more time and lots of memory [15] .

− Speed of processing is a main drawback of RSA algorithm to each of hardware or software execution [15] .

− DSA needs for more time of processing, computational overhead and increased key storage necessity.

− DSA consumes a big amount of computing resources like CPU time, battery power, and memory.

− ECDSA shares three points publicly which makes it feasible for an adversary to measure the private key of the signer.

− ECDSA performances depend on most expensive operation i.e. scalar multiplication, elliptic curve point multiplication and modular inversion operation. These unsolved problems are considered as good new research opportunities for researchers a digital signature field.

8. Conclusion

Due to the increase of online transactions on the Internet, the importance of authentication continues to increase. Thus, there is a need for us to develop mechanism for an authentication of computer-based information. One of the authentication mechanisms is a digital signature. And also digital signature can provide authorization and non-repudiation in information security field. This paper gives deep insight for original digital signature schemes and recently improvement schemes. It described a brief survey of some proposed schemes to improve traditional digital signature schemes RSA, DSA and ECDSA. The improvements in original schemes are achieved from several perspectives. In RSA scheme, it is fault tolerance perspective, while in DSA, they are speed of operation computational perspective and longtime of computations perspective. And in ECDSA, they are efficiency perspective and speed of operation computational perspective. Then it offers a comparative study between original and improved schemes.

Acknowledgements

We would like to thank to Dr. Jayaprakash Kar for his valuable suggestions and comments that helped im- proving this works. This support is greatly appreciated.

Cite this paper

Alaa D.Alrehily,Asmaa F.Alotaibi,Suzan B.Almutairy,Mashael S.Alqhtani,JayaprakashKar, (2015) Conventional and Improved Digital Signature Scheme: A Comparative Study. Journal of Information Security,06,59-67. doi: 10.4236/jis.2015.61007

References

NOTES

^*Corresponding author.