Materials Sciences and Applications
Vol.06 No.10(2015), Article ID:60858,17 pages
10.4236/msa.2015.610092
Numerical Simulation of Microstructural Evolution via Phase-Field Model Coupled to the Solutal Interaction Mechanism
Alexandre Furtado Ferreira*, Ingrid Meirelles Salvino Tomaskewski, Késsia Gomes Paradela, Dimas Moraes da Silva, Roberto Carlos Sales
Graduate Program on Metallurgical Engineering, Graduate Program on Mechanical Engineering, Federal Fluminense University, Volta Redonda, Brazil
Email: *furtado@metal.eeimvr.uff.br
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 3 July 2015; accepted 27 October 2015; published 30 October 2015
ABSTRACT
A phase-field model coupled to the multiphase/multiscale model is used to simulate the microstructural morphology and predict the CET during solidification. The considered mechanism for the CET is based on interactions of solute between the equiaxed grains and the advancing columnar front. The results for the solute concentration in liquid region, dendrite tip velocity, volume fraction of the liquid and solid are presented and discussed. The phase-field model is used to simulate the dendritic morphology of an alloy directionally solidified, by imposing a constant temperature gradient. The simulation of the equiaxed grains growth requires a further important element, the growth of grains with different crystallographic orientations. The grain orientations are generated randomly for each nucleus introduced in computational domain. Finally, the coupling results between the multiphase/multiscale model and phase-field are presented and discussed. For higher nuclei density present in the melt, a shorter distance between mold wall and the equiaxed zone in the solidification process can be observed. A solute concentration boundary layer exists in the liquid along the columnar grain contour. The concentrations in the solid indicate the presence of a microsegregation pattern. The simulated results show that the solidification features are consistent with those observed based on the metallographic examinations of cast microstructures reported in the literature.
Keywords:
Columnar-to-Equiaxed Transition, Directional Solidification, Al-Cu Alloy

1. Introduction
Solidification is the main phenomenon taking place during casting. This, in turn, has long been known as a relatively inexpensive means for producing metal goods. Nowadays, a sizable portion of the concepts and methods developed over the years in support of the research into solidification phenomena can be successfully and economically translated to industrial scale. Noticeable improvement can thereby be achieved insofar as the quality of the pieces manufactured by solidification is concerned. For this reason, solidification studies are not just mandatory; they truly are a powerful industrial tool. For conventional technologies, thorough understanding and control of the solidification process open wide perspectives in terms of its economic potential, since it provides the shortest distance from metal input to final product. As a consequence, solidification is one of the most important specialties in Metallurgy and Materials Science. In-the-mold solidification of a metal, opposite to what may, at first, be surmised, is not a “passive” process in any way. On the contrary, the metal undergoes a liquid- to-solid transformation of a very dynamic nature. In its course, events take place―like nucleation and growth of dendritic structures―which, in the absence of a tight control, may compromise the final output or even halt the manufacturing process altogether. Such events can originate several types of material heterogeneities which drastically affect the metallurgical quality of the final product [1] . The dendrites are among the most common microstructures in metals and alloys at the end of solidification. Its shapes, sizes and chemical characteristics have an important impact on the properties of the final products. The conditions for the transformation from liquid to solid, such as the temperature gradient and the growth rate, vary from process to process and in one process they are also as a function of time and space. These variations, together with the different alloy composition, lead to a multitude of microstructures and therefore material behavior. Dendritic structures observed in most casting processes of metallic alloys are the result of a competition between the growth of several arrays of dendrites that develop during solidification process under constrained and unconstrained conditions. One important transition which has to be well controlled is the so-called columnar-to-equiaxed transition (CET) [2] . The prediction of the CET is of great interest for the evaluation and design of the mechanical properties of solidified products. To this aim, it is necessary to understand the CET mechanisms and to develop a model to quantify important features of the microstructures. As suggested by many previous studies, the CET, caused by the competition between columnar and equiaxed growth, is primarily governed by such casting parameters as the alloy composition, pouring superheat, nuclei density present in the melt, cooling capacity at the metal/mold interface, and melt convection. A change from columnar to equiaxed grains is a common occurrence in metal alloy castings, and numerous mechanisms for the CET have been proposed based on experimental evidences. Mathematical modeling of the CET is limited owing to the complex interplay of macroscopic phenomena, such as heat transfer, fluid flow, and microscopic phenomena, such as nucleation and dendritic growth [3] . Typically, all previous CET models neglect or oversimplify the treatment of movement of equiaxed grains. The equiaxed grains are assumed to nucleate and grow in the constitutionally undercooled liquid ahead of the advancing columnar front [4] . The CET occurs when the advance of the columnar front is blocked by the equiaxed grains. The CET models can be classified as stochastic or deterministic. Stochastic models aim to follow the nucleation and growth of each individual grain. Its main limitation is related to the large amount of computer resources needed to resolve the large number of grains potentially present in a casting [5] - [7] . Deterministic models, on the other hand, do not attempt to resolve the nucleation and growth of each grain. Instead, they rely on averaged quantities and equations that are solved on a macroscopic scale. By tracking the columnar front movement and calculating the growth of equiaxed grains in the undercooled liquid in front of it, the CET can be predicted [3] [8] - [15] . In both stochastic and deterministic models, the evolution of grain morphology and the competitive growth between columnar and equiaxed grains during the solidification process are not considered. For a number of years now, appreciable attention has been paid, in open literature, to the simulation of dendrite growth and related phenomena. Several different numerical approaches were proposed to that end. Some works have focused on pure materials [16] - [18] , whereas others take heed of multicomponent alloys of metallurgical interest [1] [19] - [22] . In particular, the phase-field model has garnered wide acceptance, given its ability to simulate the solidification process in the presence of a complicated solid-liquid interface. The seminal work on the model is presented in [23] , dating back to the early 1980s. A collection of models has stemmed from that paper, ever since. The reason by which we adopt aluminum alloy (Al-Cu) in this work is that the aluminum nowadays is the leading non-ferrous metal in use, finding ever more applications in sectors as varied as aeronautics, beverage containers, construction and energy transportation. The qualities of aluminum and its alloys are deciding factors for designers, manufacturers and industrial users who are always on the lookout for better-performing materials. In this present study, the microstructural evolution and competitive growth from onset of solidification process in Al-0.013 mol% Cu alloy under a constant cooling rate are simulated. A phase-field model coupled to the multiphase/multiscale model is used to simulate the morphology of columnar grains and equiaxed and predict the columnar-to-equiaxed transition (CET) during solidification of said binary alloy. It is in this general framework that the present study is developed, with a focus on Al-Cu binary alloy and phase-field model coupled to the multiphase/multiscale model implemented via finite differences method in the explicit form.
2. Governing Equation
First of all, we present the governing equations the multiphase/multiscale model. This model is used to predict the CET. Then, equations of phase-field model are presented and discussed.
2.1. The Multiphase/Multiscale Model
The governing equations are based directly as in [3] and [13] . Therefore, the equations are only briefly described, followed by detailed comments on the features of the present model. To separate the various regions present in dendritic solidification, three phases are defined within a representative elementary volume (REV): solid (s), interdendritic liquid (d), and extradendritic liquid (l). The volume factions are introduced in the model as follows:
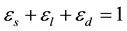 (1)
(1)
where es is solid, el is the extradendritic liquid and ed represents the interdendritic liquid. As shown in Figure 1, the inter- and extradendritic liquids are separated by a grain envelope that is a smooth surface extending around the dendrite tips.
The grain envelope volume fraction is defined as . The internal solid volume fraction can be defined as
. The internal solid volume fraction can be defined as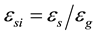 . When the internal solid fraction is unity, the equiaxed grains are said to be globulitic (i.e., fully solid globules). The interdendritic liquid is associated with the relatively small length scale of the spaces between the dendrite arms inside the envelope and is assumed to be solutally well mixed at the liquidus concentration (
. When the internal solid fraction is unity, the equiaxed grains are said to be globulitic (i.e., fully solid globules). The interdendritic liquid is associated with the relatively small length scale of the spaces between the dendrite arms inside the envelope and is assumed to be solutally well mixed at the liquidus concentration ( ) given by the phase diagram at the temperature T. The extradendritic liquid, on the other hand, is associated with the larger length scale. When its average solute concentration (Cl) is below
) given by the phase diagram at the temperature T. The extradendritic liquid, on the other hand, is associated with the larger length scale. When its average solute concentration (Cl) is below , the extradendritic liquid is undercooled. It is this undercooling that primarily drives the dendritic growth. Due to solute rejection by the growing dendrites/grains into the finite extradendritic liquid, Cl can become greater than C0 (initial concentration). The presence of a solute profile in the solid in Figure 1 reflects the fact that the mass diffusivity of the solid (Ds) is much smaller than that of the liquid (Dl), this results in incomplete solute diffusion in the solid. In fact, back-diffusion in the solid is neglected in the present study for the multiphase/multiscale model. For the one-dimensional system considered in the present study used to predict the CET during solidification of Al-Cu binary alloys, the interdendritic liquid solute and extradendritic liquid solute can be written, respectively, as in [3] [13]
, the extradendritic liquid is undercooled. It is this undercooling that primarily drives the dendritic growth. Due to solute rejection by the growing dendrites/grains into the finite extradendritic liquid, Cl can become greater than C0 (initial concentration). The presence of a solute profile in the solid in Figure 1 reflects the fact that the mass diffusivity of the solid (Ds) is much smaller than that of the liquid (Dl), this results in incomplete solute diffusion in the solid. In fact, back-diffusion in the solid is neglected in the present study for the multiphase/multiscale model. For the one-dimensional system considered in the present study used to predict the CET during solidification of Al-Cu binary alloys, the interdendritic liquid solute and extradendritic liquid solute can be written, respectively, as in [3] [13]
Figure 1. Schematic illustration of a dendrite envelope.
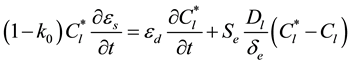 (2)
(2)
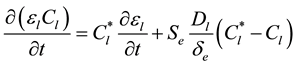 (3)
(3)
where k0 is the solute partition coefficient and Se represents the envelope area of grains. The last term in equation (2) and (3) accounts for diffusion of solute from the dendritic growth into the undercooled extradendritic liquid. The de represents the diffusion length and it is discussed in greater details in [3] . The previous equations are coupled by the liquidus line of a binary equilibrium phase diagram, i.e.,
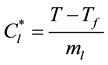 (4)
(4)
where Tf is the melting point of the pure metal, and ml is the liquidus line slope. Then, Equation (2) can be solved for the solid fraction, es, and Equation (3) provide the average solute concentration in the extradendritic liquid, Cl. The following equation is used to calculate the grain (or extradendritic liquid) volume fraction:
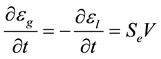 (5)
(5)
where V is the dendrite tip velocity [14]
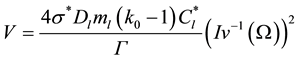 (6)
(6)
where
 is the stability constant [3] ,
is the stability constant [3] ,
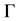 is the Gibbs−Thomson coefficient, and
is the Gibbs−Thomson coefficient, and
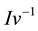 is the inverse of the Ivantsov function, which can be approximated by the following equation [13] :
is the inverse of the Ivantsov function, which can be approximated by the following equation [13] :
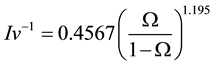 (7)
(7)
The dimensionless undercooling (W) is defined as
 (8)
(8)
Note that in Equation (8) the undercooling is defined relative to average solute concentration in the undercooled extradendritic liquid





equiaxed:


As proposed in [3] , it is assumed that nuclei appear instantaneously at a liquid region undercooled. Another issue in modeling the solute diffusion into the extradendritic liquid is the shape of the dendrite envelopes. As in [13] is assumed a spherical shape for the equiaxed grain envelopes and a cylindrical shape for the columnar envelopes. In this present study, we adopted a simpler method, where the basic envelope shape is spherical for both columnar and equiaxed growth. While this approximation may seem inadequate for columnar growth, it was verified to result in only minor differences in results [3] . This way, the spherical envelope shape is introduced in the model as in [13] :

The envelope diffusion length (de) is calculated as a function of the envelope Peclet number (Pe), from

where the instantaneous envelope radius (Re) is given by.

The Equation (11) differs slightly from the one proposed in [13] , its derivation and a closed-form analytical solution are provided in details in the [3] . The main new feature of the model proposed in [3] is that both the equiaxed and columnar dendrite growth velocities are controlled by a solutal undercooling proportional to the difference between the local liquidus concentration and the local average solute concentration in the extradendritic liquid (Equation (8)). At least for columnar growth, all other models [7] [8] [11] - [13] [24] used the initial alloy composition C0 instead of Cl in the dimensionless undercooling. Governing equations of phase-field model are presented in the following section.
2.2. The Phase-Field Model
In phase-field models, the state of the domain is customarily represented by a distribution of the single variable known as the “order parameter” or “phase-field variable,” here represented by the Greek letter f. In this present study, it is assumed that the solid state corresponds to a value of +1 for the order parameter, while, in the liquid region, f is taken to be 0. The region through which f decreases from +1 to 0 is defined as the solid/liquid interface [35] . For simulation of microstructures in binary alloys during solidification, we used two equations: one for solute concentrations, the other for the phase field itself [25] .

The evolution of the solid region with time






In this equation D(f) is the solute diffusivity in the solid and in the liquid regions. The model carried out, takes into account solute diffusivity in the liquid and in the interface regions. The “smoothing” function h(f) and the function g(f), which models the surface tension effect around the interface, are defined as [17]


Equations (15) and (16) are widely employed in phase-field works. Notice



where de gauges the anisotropy. The value j controls the number of preferential growth directions. For example, with j = 0 we shall be looking at a perfectly isotropic case, while j = 4 is indicative of a dendrite with four preferential growth directions. Orientation of the maximum-anisotropy interface is identified by the q0 of Equation (17). Furthermore, e0 in that equation, and w in Equation (13) are model parameters associated with interface energy (s) and thickness (2l), respectively, according to the following expressions [27] :




where me is the slope of the liquidus line at equilibrium, ke is the equilibrium partition coefficient, Di is the diffusion coefficient in the interface region, and the kinetic coefficient, b, is defined to be the inverse of the usual linear kinetic coefficient, m.k.. For the binary alloy system, we use the same parameters shown in the [22] . To simulate growth of an asymmetrical dendrite, it is necessary to introduce a noise term on the right-hand side of Equation (13), the phase-field equation. A usual expression for this noise is [1]

with “r” a random number between −1 and +1. The “a” parameter is the noise amplitude. Maximum noise corresponds to f = 0.5, at the center of the interface, whereas at f = 0 (liquid region) and f = 1 (solid region) there occurs no noise. That is to say, noise is generated at the interface. The Equations (13) and (14) were solved numerically. They were discretized on uniform grids using an explicit finite scheme.
3. Results and Discussions
The main objective of the present work is to propose a numerical simulation of microstructure evolution by phase-field method coupled to the solutal interaction mechanism for the columnar-to-equiaxed transition (CET). First of all, we show results of the CET model, and then, results obtained by phase-field method are presented, and finally the results of coupling between CET model and phase-field. Simulations in this present study are carried out disregarding the energy equation and instead imposing the following linear temperature profile:

where T0 is the initial temperature and

3.1. Results of Multiphase/Multiscale Model
We begin by displaying the results obtained with help of the CET model for predictions of temporal evolution of the equiaxed grain volume fraction in the two cases. The solutal interactions are quantitatively examined in this section for purely equiaxed growth. Simulations are performed for a cooling rate of 0.005 K/s. The results are presented for two different equiaxed nuclei densities equal to 2.4 × 10+5 and 8.8 × 10+6 m−3. According to Equa-
Table 1. Physical properties of Al-Cu alloy.
tion (9), these nuclei densities give the following characteristic half-spacings for the equiaxed grains, respectively: Rf = 10 and 3 mm. Figure 2 shows the temporal evolution of the equiaxed grain volume fraction (eg) in the that cases, together with the temperature variation. The present work and literature [3] data are plotted for comparison (Figure 2). When compared the present work results and with those in [3] , one can see an excellent quantitative agreement between them. It is useful to first focus on the curves corresponding to the largest nucleus densities, n = 2.4 × 10+5 m−3. One can see from Figure 2 that grain growth is initially very slow, until about 200 seconds, which can be attributed to the small values of the envelope area concentration (Se) in Equation (10). Starting at 200 seconds, the grains undergo a period of rapid growth until the grain volume fraction (eg) reaches values of about 0.95 at 350 seconds. This rapid increase in grain volume fraction (eg) can be attributed to Se in Equation (10) and to the solutal undercooling in Equation (8) for the dendrite tip velocity simultaneously reaching larger values. The time when the solutal undercooling (W) in Equation (8) reaches a negligibly small value and dendritic growth ceases is marked as an asterisk in Figure 2. This asterisk is labeled “CET” and, indicates that if columnar grains were present, they would stop growing too. A similar result is obtained for the case with nucleus densities equal to 8.8 × 10+6 m−3, except that the undercooling dissipates earlier due to the somewhat larger values of Se at early times. Also, the maximum equiaxed grain fraction, corresponding to the time when the undercooling vanishes, is about 0.7.
Through of numerical example (Figure 2), the sensitivity of the columnar-to-equiaxed transition (CET) with the nucleus density is demonstrated. Figure 3 shows the solute concentration in both the interdendritic and extradendritic liquid during the solidification process.
Figure 3 shows the corresponding variations in the liquid solute concentrations during the solidification process. One can see solute concentration in extradendritic liquid


The two different cases shown in Figure 4 illustrate why the present model can result in different CET predictions. Both cases are characterized by same temperature gradient and alloy composition, but different columnar front velocities. For n = 8.8 × 10+6 m−3 case, the equiaxed grain density is relatively large, as would case if an inoculants (grain refiner) had been used, one can see from Figure 4 the grain growth until about 220 seconds, after that, the velocity of front columnar decreases fast to the zero, indicating that CET has already occurred. For n = 2.4 × 10+5 m−3 case, the curve profile is similar to the previous case, i.e., one can see for said case that the columnar front velocity is initially very slow until 40 seconds, after this, the velocity undergo a abrupt increase until reaches a maximum value of about 8.5 × 10−5 m/s at 320 seconds, then decreases to zero, it indicates that columnar grains stopped growing, and the CET occurred too. Both velocity and position curves are consistent; because when velocity decreases to zero the columnar front position becomes constant at the time. One can see, that at the time when the velocity is zero (at about 340 seconds), the columnar front position is constant. The
Figure 2. Effect of the equiaxed nuclei densities (n) on the columnar-to-equiaxed transition (CET) of an Al-0.013 mol% Cu alloy cooled at a constant rate
Figure 3. Variation of the extradendritic and interdendritic liquid concentration during the solidification time.
Figure 4. Dendrite tip velocity and columnar front position versus time solidification.
knowledge of the columnar front position is needed in order to decide which equation to use to calculate the characteristic half-spacing (Rf). The model results indicate that the CET occurred when the columnar front position has a maximum and the velocity of the columnar front is almost zero (Figure 4). Figure 4 shows the temporal evolution of the extradendritic liquid (l), solid (s) and interdendritic liquid (d) calculated for the 2.4 × 10+5 m−3 case. One can see that, until about 200 seconds the control volume is totally extradendritic liquid. As said liquid decreases both the solid and interdendritic liquid increases until about 350 seconds. At the 350 seconds, the equiaxed grains have enough time to reach a sufficiently high volume fraction to block the columnar grains growth. In this time, the extradendritic liquid fraction (l) becomes very small and the control volume is almost totally solid (s) and interdendritic liquid (d). Starting at 350 seconds, the solid fraction keeps the growth, while interdendritic liquid (d) decreases, i.e., from that time the interdendritic liquid (d) becomes solid. An interesting behavior concerning progress of solidification can be observed through results in Figure 5, the interdendritic liquid (d) is the last to solidify, because the rejected solute from solid enriches the interdendritic liquid (d) and it decreases the liquidus temperature. That blocking between grains is the CET, and the result in Figure 5 is in agreement with those of Figure 2.
In this subsection, we present the results for numerical simulation of solutal interaction mechanism for the columnar-to-equiaxed transition. The results obtained by phase-field model are presented in the following subsection.
3.2. Phase-Field Model Results
To calculate the governing equations, there are seven unknown values. Three of them are phase-field parameters. W and e are determined by solving Equations (18) and (19) simultaneously. Since the phase-field mobility is a function of temperature, it should be calculated with the temperature during the computation. The values of solute concentration in liquid, cL, and solid, cS, are also required; they are determined from Equation (14) depending on the values of f and c at each point and every time step. The governing Equations (13) and (14) above are solved numerically, using a finite-difference scheme. In the calculations, the system temperature is uniform and continuously decreased with a constant cooling rate from the initial temperature (T0), which is slightly lower than the liquidus temperature of the Al-Cu alloy. We analyze columnar growth in a two-dimensional system. The phase field model is used to calculate the alloy directionally solidified from left to the right side of computational domain, by imposing a constant temperature gradient in an undercooled melts system. Solidification in the presence of walls is of great practical importance. In casting, solidification usually starts by heterogeneous crystal nucleation on the walls of the mold. Those crystals that grow from mold walls are known as columnar dendritic grains. The concentration field, growth and selection of columnar dendritic grains with constant cooling rate equal to 0.005 K/s for Al-0.013 mol% Cu are shown in Figure 6. In the said figure, the gray scale
Figure 5. Volume fraction for extradendritic liquid, solid and interdendritic liquid versus time solidification in seconds.
Figure 6. Simulation of the advancing of the columnar front with a cooling rate of 0.005 K/s. (a) early stage of arm growth, t = 0.062 sec; (b) arm growth and selection, t = 0.083 sec; (c) coarsening of arm, t = 0.200 sec.
represents solute concentration, while the white represents the concentration of the segregated copper from solid to liquid region. The copper concentration in solid is much less than that of copper in liquid. All the columnar dendritic grains are growing from left surface but the shapes of the arms are different from each other due to the imposed noise by Equation (22). In this simulation, a fine solid layer was added to left side of the domain boundaries.
During the calculations, the system temperature is uniform and continuously decreased with a constant cooling rate from the initial temperature of 922 K, which is slightly lower than the liquidus temperature of the Al-0.013 mol% Cu alloy. The advanced columnar grains in Figure 6(a) grows preferably, grains stop advancing or slightly melt back (Figure 6(b)). After the selection of the columnar grains, the coarsening of the selected grains is observed in Figure 6(c). In this way phase-field calculation shows the columnar selection and the columnar spacing occurs sequentially. In the phase-field model, initial solid seeds are physically selected to grow or shrink. It should be observed that the spacing between columnar grains depends on the competitive growth of grains during solidification. During the beginning of the solidification process, the competitive growth between columnar grains is more intense and the spacing between them is narrow. The competitive growth of grains becomes less intensive with the advance of the columnar grains into the liquid region. In this present simulation, the competitive growth and selection of columnar grain are successfully reproduced. With the exception of extremely pure materials, even nucleation in the bulk liquid happens mostly via a heterogeneous mechanism, i.e., on the surface of suspended foreign particles. This way, particulate additives are widely used as grain refiners to reduce grain size by enhancing the nucleation rate. Most functional and structural materials consist of an assembly of small grains of different orientations, which can vary in size from few nanometers to several hundred microns, the physical properties of polycrystalline materials are strongly influenced by them. In order to simulate the growth of equiaxed grains, the phase-field model also has been used to address problems with multi-den- dritic growth into liquid region with a constant cooling rate equal to 0.005 K/s and initial temperature of 922 K (Figure 7). Simulation of the equiaxed grains growth requires a further important element, the growth of equiaxed grains with different crystallographic orientations. Nuclei of same size were artificially introduced in computational domain to mimic the nucleation in the liquid region. The grain orientations between 0 and +1 are generated randomly for each nucleus introduced in computational domain. The growth process of six dendrites is shown in Figure 7. The snapshots correspond to the growth time of 3.4 × 10−3 sec, 8.8 × 10−3 sec, and 2.38 × 10−2 sec are shown in Figures 7(a)-(c). The equiaxed grains grow faster along the crystallographic orientations. At the early stage, as shown in Figure 7(a) and Figure 7(b), the equiaxed grains with different orientations grows freely and independently. In Figure 7(c), with increase of time, the grains begin to coalesce and impinge the adjacent grains. The advanced equiaxed grains in Figure 7(c) grow and other grains stop advancing or slightly melt back.
The competitive growth of these grains during solidification process can be observed. Due to the solute redistribution from solid to liquid region, the interdendritic liquid just ahead of the interface always has a composition greater than liquid region distant of solid-liquid interface. While the copper concentration in solid region is the lowest, the highest concentration corresponds to the interdendritic liquid. The simulation patterns of dendritic growth shows typical equiaxed grains structure, and comparing these simulations (Figures 7(a)-(c)), one can see that the equiaxed grains structure is very sensitive to the competitive growth. The results of the coupled models are showed in the following subsection.
3.3. Results of Coupling between the Multiphase/Multiscale Model and Phase-Field Model
In spite of phase-field models being suitable for simulating solidification processes, they suffer from low computational efficiency. For example, for computation of a dendrite with side-branches, i.e. secondary and tertiary arms, the computational domain should be discretized into one millions points. Thus, the computational stability condition in an explicit finite scheme can be guaranteed only with a very small time step [18] . From Figure 2, one can see that the columnar-to-equiaxed transition (CET) occurs earlier for high nuclei density. For this reason, we increased artificially the nuclei density (n = 8.4 × 10+12 and 24.8 × 10+12 m−3), in order reduce the solidification time and consequently the computer run time. With the increase in nuclei density in the bulk liquid, more equiaxed grains are nucleated. This, in turn, leads to a finer grain size in casting. Grain refinement by inoculation involves addition of particles which can act as substrates for heterogeneous nucleation. Inoculation is particularly widely practiced in the aluminium industry [28] . Figure 8 shows the profile of grain volume fraction (eg) versus solidification time, in which the columnar-to-equiaxed transition (CET) can be determined. Despite of the profiles for the two cases are qualitatively similar (Figure 2 and Figure 8). Quantitatively, it can be anticipated than the columnar-to-equiaxed transition (CET) occurs earlier when the Al-Cu alloy has a higher nuclei density present in the melt.
For nuclei density equal to 8.4 × 10+12 m−3, one can see that columnar-to-equiaxed transition takes place at 0.2 seconds. On the other hand, for a value equal to 24.8 × 10+12 m−3, the columnar-to-equiaxed transition takes place earlier to the 0.13 seconds. This transition times are input data for phase-field model, the results are showed to following.
Figures 9(a)-(d) show the morphology of dendrites which are calculated for an initial concentration of 0.013 mole fraction. To simulate the chill effect near the mould wall, a fine solid layer was added at the bottom of
Figure 7. Simulation of the multiple dendrite growth of Al-Cu binary alloy under cooling rate of 0.005 K/s. (a) early growth stage of the equiaxed grains, t = 3.4 × 10−3 sec; (b) the equiaxed grains grow freely and independently in the liquid region, t = 8.8 × 10−3 sec; (c) finally, the impingement on one another equiaxed grain with orientation different of growth, t = 2.36 × 10−2 sec.
Figure 8. The grain volume fraction versus solidification time, for a nuclei density equal to 8.4 × 10+12 and 24.8 × 10+12 m−3.
Figure 9. Numerical simulation of the morphology dendritic of an Al-0.013 mol% Cu alloy with solidification time of (a) 0.087 sec; (b) 0.17 sec; (c) 0.25 sec; (d) 0.32 sec.
the computational domain before simulation. The fine solid layer becomes unstable in a supercooled domain, with branching advancing into the liquid region (Figure 9(a)). One can see that some grains grew from solid layer and only few long columnar grains succeed in growing due to the competitive nature of the growth (Figure 9(b)). Figure 9(c) shows the formed equiaxed grains in random directions in the liquid region ahead of the columnar zone, in this way, the advance of the columnar front is blocked by the equiaxed grains. That way, the columnar grains shall have their growth inhibited and the columnar-to-equiaxed transition (CET) can be determined. The concentration field during grain growth is depicted in that figure. In the picture, the color scale represents solute concentration; so to speak, the white represents the concentration of the segregated solute from the solid to the liquid region, while the dark gray is the solute concentration in the solid region. Note that the solute concentration is higher between dendrites/grains. Due to solute rejection by the growing dendrites/grains into the liquid region, the extradendritic liquid concentration ( ) becomes equal to interdendritic liquid concentration ( ) (Figure 9(c) and Figure 9(d)). Figure 10 illustrates the microstructure evolution during the columnar-to-equiaxed transition (CET) for a nuclei density equal to 24.8 × 10+12 m−3. For the said density, the columnar-to-equiaxed transition takes place at 0.13 seconds, which is determined by multiphase/multiscale model, as previously indicated in Figure 8.
Through comparison between Figure 9 and Figure 10, which presents the dendritic morphology during the solidification process for an Al-0.013 mol% Cu alloy, one can see before columnar-to-equiaxed transition (CET), the two-dimensional simulations presents columnar dendrites similar (Figure 9(a) and Figure 10(a)). However, after columnar-to-equiaxed transition (CET), Figure 10(c) and Figure 10(d) show smaller columnar dendrites, as expected, for a higher nuclei density present in the melt, at a shorter distance between mold wall and the equiaxed zone. The simulated results showed that the solidification features are consistent with those observed based on the metallographic examinations of cast microstructures reported in the literature [31] [32] and [34] .
Figure 10. Numerical simulation of the dendritic morphology of an Al-0.013 mol% Cu alloy with solidification time of (a) 0.0815 sec; (b) 0.1039 sec; (c) 0.157 sec; (d) 0.309 sec.
During the solidification process the extradendritic liquid (l) decreases, while both solid (s) and interdendritic liquid (d) increase gradually through that period. After the columnar-to-equiaxed transition (CET), the said interdendritic liquid begins to solidify, suggesting that solidification process approaches its ending (Figure 5). In response to columnar-to-equiaxed transition (CET), the extradendritic liquid concentration (Cl) increases very rapidly to interdendritic liquid concentration ( ) (Figure 3), while growth velocity of columnar grains approaches zero (Figure 4). It should be noted that in Equation (8) the undercooling is defined relative to the average solute concentration in the undercooled extradendritic liquid, Cl. In the [2] , [8] and [11] is used instead the initial alloy composition, C0, to determine the undercooling for dendrite growth. In the [13] adopted Cl for equiaxed growth, but C0 for columnar growth. In this present study, Cl is used for both equiaxed and columnar growth. This difference constitutes the main new feature of the CET model. The dendritic morphology during the columnar-to-equiaxed transition (CET) in directional solidification is simulated using the phase-field model. The model relies on the solute conservation equation (Equation (14)) and a phase-field equation (Equation (13)) on the scale of the developing microstructure. A solute entrapment can be observed in the region next to the columnar grains and equiaxed (Figure 9 and Figure 10). Therefore, these regions are richest in solute. As result, the solidification temperature is lower for those regions. With a greater solute concentration and lower solidification temperatures, these will tend to be the last parts to solidify. A solute concentration boundary layer exists in the liquid along the columnar grain contour. In this boundary layer, the concentration decreases exponentially to C0. The concentrations in the solid indicate the presence of a microsegregation pattern. It should be observed that the phase-field calculations physically reproduces competitive growth of the columnar grains from the perturbed interface (Figure 9(a) and Figure 9(b)), the final arms spacing are independent of initial conditions, as discussed in [22] . On the other hand, spacing between columnar grains depends on the competitive growth of them during solidification. Thus, at the onset of solidification, the competitive growth is intense, which decreases with time during any solidification process (Figure 9(a) and Figure 9(b)).
4. Conclusion
A model based on coupling between the multiphase/multiscale model and phase-field was proposed in the present study. The multiphase/multiscale model proposed in the [3] was applied to predict the columnar-to-equiaxed transition (CET) in the solidification of Al-Cu alloy. The main feature of model is the concept of solutal blocking of the columnar front, which is opposed to a mechanical blocking criterion based on a critical equiaxed grain fraction, as introduced in [8] . The solute blocking effect is achieved in the model by basing the undercooling that drives dendrite tip growth on the average solute concentration of the liquid surrounding the grain envelopes (extradendritic liquid), instead of the initial alloy composition (C0). The columnar-to-equiaxed transition (CET) will occur, when the solute rejected from the equiaxed grains is sufficient to dissipate the solutal undercooling at
the columnar front, such that Cl has increased to
the columnar-to-equiaxed transition (CET) is strongly influenced by nuclei density (n), as suggested by previous studies [31] - [33] . The time of columnar-to-equiaxed transition (CET), in turn, is used as an input data for phase- field model. Thus, the phase-field model is used as computational method to simulate the microstructural morphology of columnar and equiaxed grains during any solidification process. Phase-field models have become popular in the field of structure evolution in solidification because of their capability for accurate and grid-in- dependent simulations of alloy solidification at the scale of microstructure. Their chief advantage is to avoid the explicit interface tracking by the introduction of a phase field variable, f(x, y, t), which takes on constant values in the bulk phases and varies smoothly but steeply in a diffuse interface region. The phase field method is a powerful algorithm to simulate the evolution of S/L interface in both 2D. The technique is capable of reproducing most of the phenomena associated with microstructure formation as competitive growth, coarsening and dendrite tip kinetics. Through phase-field model, an investigation of the columnar-to-equiaxed transition on the morphology of columnar and equiaxed grains for different nuclei density can be performed, for a binary alloy. The results show that microstructural morphology depends strongly on said nuclei density (Figure 9 and Figure 10). In the other words, the simulations showed a decrease in columnar zone length with the nuclei density increase, an effect resulting from equiaxed grains nucleated in front of columnar zone. However, the major problem is that the interface width in phase-field model has to be extremely small which limits the entire domain size and computation efficiency. It should be emphasized that the columnar-to-equiaxed transition (CET) depends on the thermal profile and inoculation on the macroscopic scale and the solute undercooling determined by the solute diffusion, dendritic morphology, and alloy composition in microscopic scale. Through model proposed in the present study, the influence of nuclei density on the columnar-to-equiaxed transition and dendritic morphology can be quantitatively simulated. On the other hand, the numerical modeling is dependent on input parameters, accuracy of phase diagram and material properties such as nuclei density, diffusion coefficient and interface energies. In order to improve the accuracy of the CET simulation, numerical models including multi-phases and fluid flow will need to be considered in future works.
Cite this paper
Alexandre FurtadoFerreira,Ingrid Meirelles SalvinoTomaskewski,Késsia GomesParadela,Dimas Moraes daSilva,Roberto CarlosSales, (2015) Numerical Simulation of Microstructural Evolution via Phase-Field Model Coupled to the Solutal Interaction Mechanism. Materials Sciences and Applications,06,907-923. doi: 10.4236/msa.2015.610092
References
- 1. Salvino, I.M., Olivé, L. and Ferreira, A.F. (2012) Simulation of Microsegregation in Multicomponent Alloys during Solidification. Steel Research International, 83, 723-732.
http://dx.doi.org/10.1002/srin.201200003 - 2. Kurz, W., Bezençon, C. and Gäumann, M. (2001) Columnar to Equiaxed Transition in Solidification Processing. Science and Technology of Advanced Materials, 2, 185-191.
http://dx.doi.org/10.1016/S1468-6996(01)00047-X - 3. Martorano, M.A., Beckermann, C. and Gandin, Ch.-A. (2003) A Solutal Interaction Mechanism for the Columnar- to-Equiaxed Transition in Alloy Solidification. Metallurgical Materials Transactions A, 34A, 1657-1674.
http://dx.doi.org/10.1007/s11661-003-0311-x - 4. Winegard, W.C. and Chalmers, B. (1954) Supercooling and Dendritic Freezing in Alloys. Transactions of American Society for Metals, 46, 1214-1223.
- 5. Spittle, J.A. and Brown, S.G.R. (1989) A Computer Simulation of the Influence of Processing Conditions on As-Cast Grain Structures. Journal of Materials Science, 24, 1777-1781.
http://dx.doi.org/10.1007/BF01105705 - 6. Zhu, P. and Smith, R.W. (1992) Dynamic Simulation of Crystal Growth by Monte Carlo. Method-I. Model Description and Kinetics. Acta Metallurgica et Materialia, 40, 683-692.
http://dx.doi.org/10.1016/0956-7151(92)90009-4 - 7. Gandin, Ch.-A. and Rappaz, M. (1994) Coupled Finite Element-Cellular Automaton Model for the Prediction Grain Structures in Solidification Process. Acta Materialia, 42, 2233-2246.
http://dx.doi.org/10.1016/0956-7151(94)90302-6 - 8. Hunt, J.D. (1984) Steady State Columnar and Equiaxed Growth of Dendrites and Eutectic. Materials Science Engineering, 65, 75-83.
http://dx.doi.org/10.1016/0025-5416(84)90201-5 - 9. Flood, S.C. and Hunt, J.D. (1987) Columnar and Equiaxed Growth: I. A Model of a Columnar Front with a Temperature Dependent Velocity. Journal of Crystal Growth, 82, 543-551.
http://dx.doi.org/10.1016/0022-0248(87)90346-0 - 10. Flood, S.C. and Hunt, J.D. (1987) Columnar and Equiaxed Growth: II. Equiaxed Growth Ahead of a Columnar Front. Journal of Crystal Growth, 82, 552-560.
http://dx.doi.org/10.1016/0022-0248(87)90347-2 - 11. Gäumann, M., Bezençon, C., Canalis, P. and Kurz, W. (2001) Single-Crystal Laser Deposition of Superalloys: Processing-Microstructure Maps. Acta Materialia, 49, 1051-1062.
http://dx.doi.org/10.1016/S1359-6454(00)00367-0 - 12. Kurz, W., Bezençon, C. and Gäumann, M. (2001) Columnar to Equiaxed Transition in Solidification Processing. Science and Technology of Advanced Materials, 2, 185-191.
http://dx.doi.org/10.1016/S1468-6996(01)00047-X - 13. Wang, C.Y. and Beckermann, C. (1994) Prediction of Columnar to Equiaxed Transition during Diffusion-Controlled Dendritic Alloy Solidification. Metallurgical Transactions A: Physical Metallurgy and Materials Science, 25A, 1081- 1093.
http://dx.doi.org/10.1007/BF02652282 - 14. Lipton, J., Glicksman, M.E. and Kurz, W. (1984) Dendritic Growth into Undercooled Alloy Metals. Materials Science Engineering, 65, 57-63.
http://dx.doi.org/10.1016/0025-5416(84)90199-X - 15. Ziv, I. and Weinberg, F. (1989) The Columnar-to-Equiaxed Transition in Al 3pct Cu. Metallurgical Transactions B: Process Metallurgy, 20B, 731-734.
http://dx.doi.org/10.1007/BF02655931 - 16. Ferreira, A.F., Silva, A.J. and Castro, J.A. (2006) Simulation of the Solidification of Pure Nickel via the Phase-Field Method. Materials Research, 9, 349-356.
http://dx.doi.org/10.1590/S1516-14392006000400002 - 17. Ferreira, A.F., Ferreira, L.O. and Assis, A.C. (2011) Numerical Simulation of the Solidification of Pure Melt by a Phase-Field Model Using an Adaptive Computation Domain. Journal of the Brazilian Society of Mechanical Sciences and Engineering, 34, 125-130.
http://dx.doi.org/10.1590/S1678-58782011000200002 - 18. Ferreira, A.F. and Castro, J.A. (2014) Phase-Field Simulations of Dendritic Crystal Growth with Focus on the Computational Efficiency. Advanced Materials Research, 1025-1026, 745-748.
http://dx.doi.org/10.4028/www.scientific.net/AMR.1025-1026.745 - 19. Ferreira, A.F. and Ferreira, L.O. (2009) Microsegregation in Fe-C-P Ternary Alloys Using a Phase-Field Model. Journal of the Brazilian Society of Mechanical Sciences and Engineering, 31, 173-180.
http://dx.doi.org/10.1590/S1678-58782009000300002 - 20. Salvino, I.M., Jácome, P.A.D., Ferreira, A.F. and Ferreira, I.L. (2012) An Analysis of the Physical Properties of Multicomponent Alloy on the Simulation Solidification by Phase-Field Model. Materials Science Forum, 730-732, 703- 708.
http://dx.doi.org/10.4028/www.scientific.net/MSF.730-732.703 - 21. Ferreira, A.F., Castro, J.A. and Ferreira, I.L. (2014) 2D Phase-Field Simulation of the Directional Solidification Process. Applied Mechanics and Materials, 704, 17-21.
http://dx.doi.org/10.4028/www.scientific.net/AMM.704.17 - 22. Ferreira, A.F., Melo, E.G. and Ferreira, L.O. (2014) Prediction of Secondary-Dendrite Arm Spacing for Binary Alloys by Means of a Phase-Field Model. Steel Research International, 85, 58-64.
- 23. Caginalp, G. and Fife, P. (1986) Phase Field Methods for Interfacial Boundaries Fife. Physical Review B: Condensed Matter and Materials Physics, 33, 7792-7794.
http://dx.doi.org/10.1103/PhysRevB.33.7792 - 24. Gandin, C.-A. (2000) From Constrained to Unconstrained Growth during Directional Solidification. Acta Materialia, 48, 2483-501.
http://dx.doi.org/10.1016/S1359-6454(00)00070-7 - 25. Ode, M. and Suzuki, T. (2002) Numerical Simulation of Initial Microstructure Evolution Fe-C Alloys Using a Phase- Field Model. ISIJ International, 42, 368-374.
http://dx.doi.org/10.2355/isijinternational.42.368 - 26. Kim, S.G., Kim, W.T. and Suzuki, T. (1998) Interfacial Compositions of Solid and Liquid in a Phase-Field Model with Finite Interface Thickness for Isothermal Solidification in Binary Alloys. Physical Review E: Statistical Physics, Plasmas, Fluids, and Related Interdisciplinary Topics, 58, 3316-3323.
http://dx.doi.org/10.1103/PhysRevE.58.3316 - 27. Liu, M.X., Wang, K., Xia, D. and Jiang, T. (2014) Phase Field Simulation of Al-Si Binary Dendritic Growth and Micro-Segregation Patterns under Convection. Journal of Alloys and Compounds, 589, 431-435.
http://dx.doi.org/10.1016/j.jallcom.2013.11.108 - 28. McCartney, D.G. (1989) Grain Refining of Aluminium and Its Alloys Using Inoculants. International Materials Reviews, 34, 247-260.
http://dx.doi.org/10.1179/imr.1989.34.1.247 - 29. Greer, A.L., Bunn, A.M., Tronche, A., Evans, P.V. and Bristow, D.J. (2000) Modelling of Inoculation of Metallic Melts: Application to Grain Refinement of Aluminium by Al-Ti-B. Acta Materialia, 48, 2823-2835.
http://dx.doi.org/10.1016/S1359-6454(00)00094-X - 30. Kurz, W., Bezençon, C. and Gäumann, M. (2001) Columnar to Equiaxed Transition in Solidification Processing. Science and Technology of Advanced Materials, 2, 185-191.
http://dx.doi.org/10.1016/S1468-6996(01)00047-X - 31. Mirihanage, W.U., Dai, H., Dong, H. and Browne D.J. (2013) Computational Modeling of Columnar to Equiaxed Transition in Alloy Solidification. Advanced Engineering Materials, 15, 216-229.
http://dx.doi.org/10.1002/adem.201200220 - 32. Canté, M.V., Cruz, K.S., Spinelli, J.E., Cheung, N. and Garcia, A. (2007) Experimental Analysis of the Columnar-to- Equiaxed Transition in Directionally Solidified Al-Ni and Al-Sn Alloys. Materials Letters, 61, 2135-2138.
http://dx.doi.org/10.1016/j.matlet.2006.08.032 - 33. Spinelli, J.E., Ferreira, I.L. and Garcia, A. (2004) Influence of Melt Convection on the Columnar to Equiaxed Transition and Microstructure of Downward Unsteady-State Directionally Solidified Sn-Pb Alloys. Journal of Alloys and Compounds, 384, 217-226.
http://dx.doi.org/10.1016/j.jallcom.2004.04.098 - 34. Ares, A.E., Gueijman, S.F. and Schvezov, C.E. (2010) An Experimental Investigation of the Columnar-to-Equiaxed Grain Transition in Aluminum-Copper Hypoeutectic and Eutectic Alloys. Journal of Crystal Growth, 312, 2154-2170.
http://dx.doi.org/10.1016/j.jcrysgro.2010.04.040 - 35. Loginova, I., Amberg, G. and Agren, J. (2001) Phase-Field Simulations of Non-Isothermal Binary Alloy Solidification. Acta Materialia, 49, 573-581.
http://dx.doi.org/10.1016/S1359-6454(00)00360-8
NOTES
*Corresponding author.













