Materials Sciences and Applications
Vol.06 No.05(2015), Article ID:56336,18 pages
10.4236/msa.2015.65045
DNA Nano Devices as a Biased Random Walk Process: A Case Study of Isothermal Ratchet?
Jean-Pierre Aimé*, Juan Elezgaray
CBMN, CNRS-University of Bordeaux, Pessac, France
Email: *jp.aime@cnanogso.org, j.elezgaray@iecb.u-bordeaux.fr
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 25 February 2015; accepted 12 May 2015; published 15 May 2015
ABSTRACT
Computation and amplification processes based on Networks of Chemical Reactions are at the heart of our understanding of the regulation and error correction of life systems. The recent advances in DNA nanotechnology, with the creation of the modular structures origamis and the development of dynamical networks using the toe hold mediated strand displacement, open fertile areas to construct Hierarchical Cascades of Chemical Reactions with an increasing complexity inspired from systems in biology. DNA strands have the great advantage to design autonomous and homogeneous Networks of Chemical Reactions leaving aside companion chemical reactions as it occurs in biological systems. In the present paper, we use the Fokker Planck equation to extract predictions that address a wider class of systems beyond the case of diluted solutions. We introduce the concept of toehold strength and output strength that leads to an exponential square dependence of the toehold strength divided by the output strength on the escape rate and the probability for the output strand to leave the gate. We highlight the influence of the boundary conditions that may have an important consequence in confined environment when modular structures like origamis are employed.
Keywords:
DNA Nanotechnology, Isothermal Ratchet, Confined Chemical Reactions, DNA Logical Gate, DNA Origami, Modular Algorithm

1. Introduction
Over the last decades, DNA became a material to conceive and fabricate news structures and functions. Thanks to N.C. Seeman approach [1] teaching that DNA was more than a genetic code material for life systems. N.C. Seeman vision constructs an orthogonal mind approach providing complete new strategies in the domain of materials where unexpected self assembled structures can be fabricated [1] -[8] . Within this framework, the creation of DNA origamis [2] is the kind of breakthrough that opens a wealth of new areas. In addition, the development of DNA nanomachines shows that chemical species may become bit units with which logical operations of increasing complexity [9] -[17] are conceived. The robustness of downstream chemical reactions cascade to build sequence of logical operations and amplification process were then demonstrated [15] [16] [18] [19] . As a result, DNA becomes a perfect support to take inspiration from biological systems. Biological systems work at any scale from nanometer to macroscopic scale. At the nanometer scale properties are often driven by noise strength. Many examples show how biological nano units take advantage of the noise forcing and bias the randomness to transduce and elaborate functions [20] [21] . DNA sequence is the simplest chemical building unit from which many remarkable structures and devices have been fabricated. In this paper we restrict our purpose to DNA devices involving motion, or displacement, of DNA strands.
In the seminal work done by B. Yurke et al. [22] was fabricated the first sequence dependence DNA motor using a toehold mediated strand displacement. The device was further improved by adding a RNase H [23] that helped to discard waste or ill formed structures. Then, processive motors along a track were conceived (for a review see Ref. [13] ). In all the cases, an asymmetry is created to biase the motion in a given direction. In the Ref. [24] , the asymmetry is created with a DNAzyme allowing a forward motion to be performed by reducing the probability for a backward step with respect to the one for a forward step. The same type of approach was used to design a prescriptive landscape on a DNA origami [25] . Another similar approach was used so that a toehold was created allowing the DNA walker to migrate on a neighboring, not cleaved, substrate [26] -[28] . In an attempt to further engineer the DNA nano devices, a remote toehold action has been proposed to control the kinetics and competing rates of the devices [29] . Others attempts use DNA topological specific properties with the same objective to sequester the active sequence until an input command is processed [15] [16] [30] . Conformational changes triggering the transformation between PX and JX2 states, (see for a review Ref. [12] ), were also done and were further developed by combining the devices with origami platform [31] .
Other approaches using DNA to design nano devices have also been developed. G sequences that form tetraplex are used with fuel strands to transform tetraplex to duplex and vice versa building an alcalin responsive nano mechanical devices [32] . Photon induced DNA conformational change through cis-trans isomerization of intercalated azobenzene molecule [5] [33] . Another interesting alternative is the use of loop-loop interaction between aptamers triggered by an external ligand [34] .
The works that motivated the present study were the numerous experimental studies and quantitative analysis made recently [9] -[11] [14] [35] where cascades of chemical reactions performed an amplification process or several logical operations [16] [18] [19] . Those cascades force a downstream flow. For the SeeSaw device, the asymmetry is not constructed on the device itself. There is no difference in length between the input and output strands. Therefore, no preferential flow can occur and one expects an equal number of free input and output strands in solution and an equal number of input and output strands hybridized on the gate template. Which makes an oriented downstream flow is that the whole equilibrium chemical reaction is biased by using a concentration of gate and fuel much larger than the working input that acts as a catalyst [14] .
What we want to emphasize is that those chemical reactions exhibit a symmetry breaking, without which no flow can occur, and make a biased random walk to happen. DNA nano devices are dynamical systems working out of equilibrium. On the other hand, to transduce the chemical energy into a mechanical work, the downstream flow involves dissipation [36] [37] . Beside the dissipation ensuring irreversibility in the process, the asymmetry of the potential well is one of the key parameters. Such a potential structure was used to describe the molecular motion of kinesin where binding events of ATP were the external chemical energy supplied allowing the motor to reach an excited, out of equilibrium, state. Here we shall disregard any possible intermediate or excited state and focus on the influence of the asymmetric potential shape with the appropriate boundary conditions that may provide new insights on the understanding of the DNA devices. In this work, we present an investigation based on the study of isothermal ratchets to analyze the specific case of the DNA strand displacement. We use a simple model; we hope heuristic enough, in which the shapes of the energy landscape and the boundary conditions are varied in order to extract simple and robust concepts that may help to design DNA devices.
2. Basic Physical Quantities
We start with an evaluation of a few physical properties when the nucleotides are bind together to form the canonical helical structure. The approach is based on a simple mechanistic approach. The Nucleotide is described as a bead in spite of the fact that it is in itself a complex unit. We also do not consider the chemical specificity and use an average bead free binding energy of about 2.5kBT [38] . The attached beads are modeled as a damped oscillator where the coupling with the surrounding medium is given by a viscous term. The unique quantities we need are the diameter of the bead we set equal to the nucleotide period f = 0.34 nm, the binding energy: U = 2.5kBT, the damping coefficient using the Stokes relationship Damp = 3phf where h is the viscosity of the water at room temperature. The values of the associate spring constant, damping coefficient and characteristic times are:
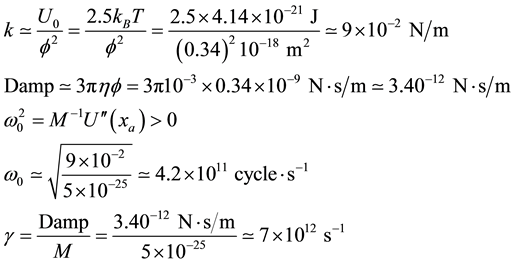
where M is the average molecular weigth of a nucleotide (300 g/mole),  the characteristic frequency of the bead at the bottom of the potential well noted A in Figure 1. The bead relaxes at a time scale of picosecond and behaves as an over damped oscillator. When one considers the motion of a nucleotide unit along a DNA strand, the characteristic times are found to reach much larger values with respect to what is expected at a microscopic molecular scale. To take into account the slow down, an usual way is to consider a thermal activated process following the Kramers approach. To generate two distinct time scales, Kramers studied a particle travelling a One-D potential with a fast intra well relaxation process we calculate to be 10−12 - 10−13 s, and a much slower inter well equilibrium time when the barrier height separating the wells is larger than kBT. Keeping this picture we evaluate the hopping rate of a basic unit. The Kramers’ expression [39] is:
the characteristic frequency of the bead at the bottom of the potential well noted A in Figure 1. The bead relaxes at a time scale of picosecond and behaves as an over damped oscillator. When one considers the motion of a nucleotide unit along a DNA strand, the characteristic times are found to reach much larger values with respect to what is expected at a microscopic molecular scale. To take into account the slow down, an usual way is to consider a thermal activated process following the Kramers approach. To generate two distinct time scales, Kramers studied a particle travelling a One-D potential with a fast intra well relaxation process we calculate to be 10−12 - 10−13 s, and a much slower inter well equilibrium time when the barrier height separating the wells is larger than kBT. Keeping this picture we evaluate the hopping rate of a basic unit. The Kramers’ expression [39] is:
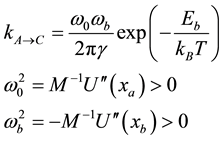
with
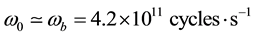
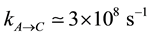 (1)
(1)
Figure 1. Sketch of a two well potential A and C and the top of the hill at point B.
The calculated rate (Equation (1)) gives a hopping time over the barrier height of a few ten nanoseconds. A much shorter time, typically 3 orders of magnitude faster than the hopping time deduced from the experimental data. Note also that the measurement of the self-diffusion of DNA gives time constants around 10−5 s [40] [41] , a time constant unusually large at this scale. Such a slow down has been interpreted as due to an additional electrostatic barriers, however it may as well be related to the hydrodynamic interaction involved in semi-rigid chains [42] .
We now evaluate the diffusion limited rate constant of DNA hybridization in dilute solutions. To calculate the diffusion constant D of a short oligonucleotide, say 10 to 20 bp long, we use the persistent length of a single strand f = 1 nm and the Einstein relationship, then the average time for the particle to diffuse over its length is computed:
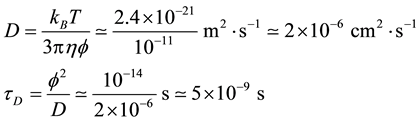
The hybridization rate is the product of the Diffusion constant and a characteristic length of the species. We use again the persistent length, and with the Avogadro number Na we get:
 (2)
(2)
while the observed second order chemical rate constant if often measured to be:
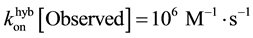

1Using a random walk description gives a total time for N steps corresponding to N nucleotides: . For N = 20, one would have 4 ms, therefore a fast process with a minor difference between two strands of 10 and 20 bp long. In most experiments and whatever the process involved when the two complementary strands touch each other, we shall not be able to decipher the probabilities of hybridisation completion as a function of the length and it is safe to use the same value of hybridisation rate.
. For N = 20, one would have 4 ms, therefore a fast process with a minor difference between two strands of 10 and 20 bp long. In most experiments and whatever the process involved when the two complementary strands touch each other, we shall not be able to decipher the probabilities of hybridisation completion as a function of the length and it is safe to use the same value of hybridisation rate.
We may argue that the hybridisation rate might depend on the length of the strands. However, even with a slow stepping time of 10 ms, the probability for a complete reaction weakly depends on the total strand migration time1. Here again, there is a 2 orders of magnitude difference between the experimental results and the calculated value. The nucleation rate borrows the same kind of feature than the one used, the Kramers result, to calculate the bead hopping rate over a potential barrier. Everything happens as if an effective barrier height of 7kBT must be added:
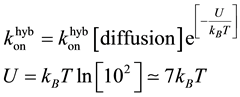
Note that this height of the activation barrier is close to the one found, U = 8kBT, to compute the diffusion constant of a protein, the Kinesin, walking along a microtubule track [43] . Taking into account this additional energy, the barrier height is roughly equivalent to 4 nucleotides, thus the hybridisation rate of giving a lower limit to trigger the pairing of strands at the rate of 10−6 M−1∙s−1. This number of nucleotides was shown to be the lowest toehold length required to reach an asymptotic plateau for an equivalent bimolecular process describing the migration with a strand displacement [9] [10] . Even if DNA hybridization is most studied, it is a hard task to get precise microscopic information that takes into account the numerous configurations available between two colliding single strands. Within the Kramers framework, this complex process is recast as an effective barrier height. The One-D translational motion approach is by far much too simple but still may provide an interesting clue when two single strands collide.
It is worth noting that the above numerical applications assume that the thermal energy is fully dedicated to the translational motion. However, only a few degrees of freedom might be able to pump the thermal energy available to activate a back or forward step along the track. As a consequence, a tiny amount of the thermal energy available may contribute to the nucleotide translational diffusion, which will lead to an overestimation of the barrier height.
The slow down is even much more pronounced when DNA migration through Holiday junction motion is considered with a stepping time ranging between the ms up to hundred of ms [44] and even reach the second: a “macrosopic time scale” [45] . For Holiday junction the stepping time shows a strong dependence on the counter ions between Mg2+ and Na+ [44] , while for a strand displacement it is found to be about 1 ms [9] [10] . There are several attempts trying to get a microscopic description of the different configurations that provide useful insights upon the effect of the single strand conformations [9] [35] [38] . Especially, a recent work points out the difference in entropy contribution between the invader strands touching the template and the first passage of the output strand leaving the template [35] .
The use of the Kramer’ approach is mostly of Heuristic interest. What we want to address is the question upon the basic ingredients we need to understand the physical origin of the strand displacement that is the transduction of a chemical energy, the folding of the toehold, to a mechanical work in confined environment and diluted solution.
3. Biased Random Walk and Strand Displacement
A Toy Model
The toy model is based on the works done to describe a ratchet device or a biased random walk [36] [37] [46] -[48] . Several problems were questioned among which the motion of proteins along a track or the biased brownien motion of particles in a fluid. The goal was to provide a model describing the motion of molecular motors where the nanometer size makes the noise strength a source of the forcing. Concepts, like the asymmetry of a potential landscape or the fluctuations of the forces and of the barrier heights, were introduced to characterize a steady flow. Another piece of work focuses on the influence of the boundary conditions. In this frame, the Hopfield description [49] can be seen as an absorbing condition together with the competing koff rates for the good and wrong molecules.
We use a simple piecewise potential that allows extracting simple analytical expressions from the Fokker- Planck equation [46] [50] [51] . The strand displacement is expressed as the motion of a particle that escapes from the asymmetric potential with two different slopes. The device is made of a DNA single strand template (the blue- red line in Figure 2), a single displaced strand usually called output strand (the blue line in Figure 2), a single invader strand, also called input, that removes the output strand and a toehold (the red part of the invader Figure 2). The toehold is a short sequence of nucleotides fixing the invader on the template and, for a sequence long enough, forcing a forward motion. The toehold is the additional sequence creating the asymmetry of the device.
The elementary unit is built with 4 or 5 nucleotides as it was discussed in the previous paragraph. Therefore, the case of a toehold made of one nucleotide will be given by a fraction of this unit either 0.25 or 0.20. Note also that, from first principle, the motion of a nucleotide will have a perfect brownien motion with an equal probability
Figure 2. (a) Sketch of a chemical reaction and DNA nano device based on the forward motion of a DNA strand initiated by a toehold DNA sequence. Input with its toehold (red) and common sequence with the output (blue) that displaces the output strand. Possible intermediate states are sketched; (b) Schematic representation of the competitive motion between the input and output strands and sketch of the toe hold mediated strand displacement as the motion of a bead in an asymmetric potential.
to move either to the left or to the right (Figure 2(b)). Therefore, the asymmetry created by a toehold only located at one end of a template must be introduced at a higher level, an elementary unit made of several nucleotides.
The toehold strength is described with a varying slope that can either be smaller or greater than that of the slope of the barrier height controlling the output strand escape rate. The biased forward motion of the invader and the displacement of the output strand are described as the motion of a bead in an asymmetric potential well (Figure 3). The bead is placed at the location x = 0 at the time t = 0 corresponding to the case where the invader sticks on the template through its toehold part. The boundary constraint is an absorption condition at the output end, the right side at x = x0, meaning that once the bead has reached the top of the barrier height it diffuses away being not allowed to go back into the potential. This absorbing condition represents the behavior of the displaced strand. Depending on the way the device is used, the boundary condition at x = -x1 can be different (see Annex 2). In solution the most appropriate is also to use an absorption condition. The potential is sketched as follow (Figure 3).
We write the potential in unit of kBT: , then as recorded on the figure:
, then as recorded on the figure:
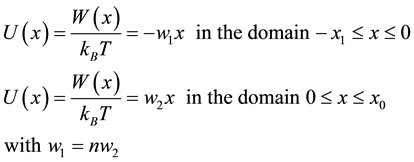 (3)
(3)
We inject a particle at x = 0 at the time t = 0, and look for the probability for the particle to be still in the well at time t. Basically, this will be given by a residence time, which is the reciprocal of the rate at which the particle escapes from the bottom up to the location x0. The time evolution of the probability follows the Fokker Planck equation:
 (4)
(4)
The current is given by:

Applying the Laplace transform, Equation (4) rewrites:
Figure 3. Scheme of the shape of the potential. The source is a bead which is inserted at x = 0 at time t = 0. Then the bead moves either to the right or to the left with the constraint that it disappears when it reaches x = x0 or x = -x1.

Equation (6) gives a characteristic equation from which it is convenient to use the notations:

In the left side, the diffusion varies as Dn2, thus the drift velocity scales as n2. Such a variation could be of interest to evaluate the kinetics competition between different configurations and has to be compare to the fluctuation time of a fluctuating barrier height of the potential [36] [52] .
With p > 0, q > 0, the physical solutions of Equation (6) are noted as a function of the coefficients A(s), B(s), C(s) and D(s) and have the form:

The coefficients A(s), B(s), C(s) and D(s) are obtained by ensuring the continuity of the probability and the current at x = 0 and the boundary conditions at x = x0 and x = -x1 (see Annex 1):
With Q(t) the probability that the particle is still in the potential well at time t, the escape rate k is given by:
Then using the Laplace transform of 


Integration of Equation (10) and using Equation (9) gives:

The coordinate x1, the location at which the bead escapes from the left, has a linear dependence with n, thus the toehold strength gives an n2 exponential dependence. The coordinate x0, the location at which the bead diffuses away when it reaches the right side end, has a linear dependence with the length of the displaced strand. Let’s note this length m, where m is a number of units. It is not obvious to give a precise number of nucleotides for a given value of U0 or n. For instance U0 = 12.5kBT might correspond to about 4 GC nucleotides, while U0 = 10kBT might correspond to 5 - 6 AT nucleotides. Therefore, it is worth using the concept of toehold strength, for n, and displaced strand strength for m, rather than a DNA length as used in experimental data.
The residence time of the bead is assimilated to the migration time of the strand and will be expressed with the reduced coordinate 



Figure 4. (a) Variation of the residence time (Equation (11)) as a function of the toehold strength n and the location x0 = m, with U0 =12.5 and m = 1 (black), m = 2 (red), m = 3 (blue). The (b) is a zoom recording the computed variation for two values of the barrier height U0:U0 = 10 black line, U0 = 12.5 red line.
For a toehold strength below n = 1, the residence time is mostly driven by the left escape rate at the x1 location. Therefore, for n < 1, the probability for the invader to leave the device is greater than the probability for the output strand to escape. For the symmetric case, which is obtained for the couple of values (n = 1, m = 1), there is an equal probability for the bead to escape either from the right (output strand) or from the left (input strand). After the maximum, the residence time decreases as the toehold strength increases reaching an asymptotic value, which is only given by the right escape rate at the x0 location. For n large enough, the escape rate no longer depends or weakly depends on the m value. This is a known result and in experiments a toehold length of 7 or 8 nucleotides (n of about 2) is often chosen.
The asymmetry of the potential shape is governed by the couple of parameters (n, m), that appears in the exponential argument as nx1/x0 (or else n2/m)2. As expected, when the output strength increases the whole curve is shifted toward the high value of n. For m = 3, the symmetric value (n = 1, m = 1) is reached for n nearly equal to 2, meaning that for n < 2 the bead mostly escapes from the left, while with m = 1 and n = 2 we expect that the bead mostly escapes from the right. In Figure 4(b) is recorded a comparison between U0 = 10 and 12.5kBT. The main difference is a decrease of 
The residence time is a function of both the left and right escape rates and does not give an unambiguous information on the output strand probability to leave the device. The probability for the bead to move forward, e.g. to the right is given by the current:

In Figure 5(a) are reported the log of the probability for the bead to escape on the right side that is the proba-
Figure 5. (a) Logarithm of the probability, computed with Equation (12), for the output strand to be removed from the template as a function of the toehold strength. Red line U0 = 10kBT; black line U0 = 12.5kBT, continuous line m = 1, dotted line m = 2, dashed line m = 3. (b) Experimental data, giving an effective migration bimolecular reaction rate, recorded by D. Y. Zhang & E. Winfree [9] [10] .
bility for the output strand to diffuse away from the device. With m = 1 a plateau is reached at a value of n slightly higher than 1, the symmetrical value where the probabilities for the bead to escape on either sides are equal. For U0 = 10kBT the probability varies over 5 orders of magnitude, while for U0 = 12.5kBT the probability varies over 6 orders of magnitude. Once the invader strand has touched the device, the probability for the output strand to escape from the right side provides a weighting value to evaluate the effective migration bimolecular rate kon showing that kon can vary from 106 to 1 M−1∙s−1 as a function of the toehold strength. The overall shape of the computed variation is in good agreement with the experimental data (Figure 5(b)) that show a smooth wavy shape on the three experimental curves [9] [10] . D.Y. Zhang did extract an effective migration bimolecular rate kon where the product of the bimolecular reaction is the output strand. Once the target has been hit it does not mean the reaction occurs, thus P = 1 corresponds to 106 M−1∙s−1 and P = 10−6 to 1 M−1∙s−1. Also it is worth recalling that n = 1 corresponds to 4 - 5 base pairs. Again, the effect of the parameter m is to shift the whole curve toward higher values of n. The model predicts that to reach the plateau with m = 3 requires to have a toehold strength about twice greater than the one required for m = 1.
An alternative to improve the computation with DNA strands is to use the DNA origamis as platforms for DNA devices. Beyond the confinement that enhances the concentration at the local scale in turn increases the speed of the chemical reaction [53] [54] (e.g. the rate kon × clocal in s−1, with clocal the concentration of DNA strands at the local scale), the close proximity of the gate with the input and fuel strands may significantly modify the reaction scheme in turn the design of the device. As a matter of fact, the close proximity of the interacting strands makes truly difficult to sequester the active part of the gate output strand. Even a drastic reduction of the toehold strength cannot avoid unwanted leaks of the devices [54] . This can be qualitatively understood with the fact that when a huge number of contacts between the gate and the invader occurs, the invader always succeeds whatever the probability of the invader to hybridize the gate provide the output strand diffuses away. To describe the tethered devices on origamis we use a reflecting boundary condition at the location x = -x1 (scheme Figure 6).
As shown on scheme 6, the potential structure is the same as the one used previously, the unique difference is the reflecting boundary condition at x = -x1 which writes:
This boundary condition seems to be a bit artificial as it forces the current to always be directed from the left to the right. However, we observed that with a seesaw gate on a origami, the fuel strand was able to trigger a gate output without the need of an input strand, something which is unlikely to happen in solution [54] .
The residence time is (see Annex 2):

In Figure 7 are shown selected results that compare the effect of the boundary conditions. The computed
Figure 6. Structure of the potential shape with a reflecting condition at x = -x1.
Figure 7. Reduced residence time as a function of the toehold strength n; Black line with the reflecting boundary condition, continuous line m = 1, dashed line m = 3 (computed with Equation (13)). Red line with the absorbing condition at x = -x1, m = 1 (computed with Equation (11)).
curves compare the behavior of the devices in diluted and confined situation once the invader has touched the gate without taking into account a local concentration effect. When the invader cannot escape, the invader can still do a work with a very weak toehold strength, case n < 1, while it cannot in diluted solution. Moreover, when the displaced strand strength is increased, case m = 3, the tethered invader remains much more efficient than the one in solution that only has to displace a shorter strand (m = 1).
4. Conclusions
The above calculation gives an exponential square dependence as a function of the toehold strength n, where n corresponds to a number of units that are not restricted to the scale of a nucleotide. This way to do, while being set in a qualitative way, is an attempt to understand the biased motion of nucleotides in DNA nano devices. There is no reason to expect a nucleotide located in the middle of the device to move preferably in either direction. The model can be seen as a modified detailed balance approach in which is added a forcing given by a toehold force scaling as
Using the Fokker Planck Equation, the shape of the escape rate, involving both sides, and the probability for the output strand to leave the gate as a function of the toehold and output strength are derived for asymptotic long time. At this stage, it is worth noting that changing the energy landscape does not change the main trends given below (see Annex 3):
The output strength leads to an exponential 
・ The invader escapes faster than the output strand for n < 1 and m = 1.
・ The output strand escapes faster than the invader for n > 1 with m = 1.
・ The residence time does not exhibit a monotonous variation as a function of the toe hold strength. The above model predicts that there is a domain (n, m) where the device is slowed, which can be of importance with respect to competitive kinetics between several different gates.
・ When m increases, there is an increasing domain of toe hold strength where the invader escapes faster than the output strand. The maximum of the residence time decreases and shifts toward higher values of n. Similarly, the probability for the output strand to leave the gate decreases with a shift toward higher values of n.
The second interest of the use of the Fokker Planck equation is to address the question upon the effect of the boundary conditions. This allows us to investigate a wider class of devices, either in solution or else arranged in a confined environment such as on an Origami nano platform or inside a vesicle. To emphasize the influence of the boundary conditions, we applied the absorbing and the reflecting condition on the side of the invader. Due to the obvious difference between these two boundary conditions, the difference is striking. When the reflecting condition is used the invader always succeeds, whatever the toehold strength, keeping in mind that it may take quite a long time as shown with the shape of the residence time (Figure 7). This result relies on the experimental difficulty we face to sequester the active part of devices tethered on origamis [54] . Following the present method, other boundary conditions can be used and could be more appropriate for tethered devices.
From the behavior of the device as a function of the couple of parameter (n, m), we extract two main predictions that may be of interest to design DNA nano devices.
In confined environment, in addition to a reduction of ever possible cross talks, we can redesign the device by reducing the size of the domains involved. For example, it might not be necessary to use fuel strands to ensure a catalytic behavior of the invader. On the opposite, as shown with the reflecting condition, we may increase the size of the template and of the output strand without reducing the efficiency of the device.
In solution it would be of interest to verify the effect of the ratio n/m, which to our knowledge had never been systematically investigated with the simplest toehold mediated strand displacement device.
Devices based on DNA strands allow building autonomous and homogeneous systems (see for instance Ref. [15] for an extensive discussion). Therefore, beyond DNA nanotechnology, the DNA strands are the simplest chemical units with which we can construct, step by step, dynamical structures that spatially organize the flow of information with competing kinetics, and thus should help our understanding of life systems where much more complex sets of intricate chemical cascades are often at work.
Acknowledgements
This work is supported by the French National Agency and the project PIA VIBBnano ANR-10-NANO-04-01 and the COST Action TD1003 “BioInspired Nanotechnologies: from concept to application”.
References
- Seeman, N.C. (2003) DNA in a Material World. Nature, 421, 427-430. http://dx.doi.org/10.1038/nature01406
- Rothemund, P.W.K. (2006) Folding DNA to Create Nanoscale Shapes and Patterns. Nature, 440, 297-302. http://dx.doi.org/10.1038/nature04586
- Dongran, H., Suchetan, P., Liu, Y. and Yan, H. (2010) Folding and Cutting DNA into Reconfigurable Topological Nanostructures. Nature Nanotechnology, 5, 712. http://dx.doi.org/10.1038/nnano.2010.193
- Douglas, S.M., Bachelet, I. and Church, G.M. (2012) A Logic-Gated Nanorobot for Targeted Transport of Molecular Payloads. Science, 335, 831-834. http://dx.doi.org/10.1126/science.1214081
- Yang, Y., Masayuki, E., Hidaka, K. and Sugiyama, H. (2012) Photocontrollable DNA Origami Nanostructures Assembling into Predesigned Multiorientational Patterns. Journal of the American Chemical Society, 134, 20645-20653. http://dx.doi.org/10.1021/ja307785r
- Yin, P., Hariadi, R., Sahu, S., Choi, H.M.T., Park, S.-H., La Bean, T.H. and Reif, J.H. (2008) Programming Molecular Tube Circumferences. Science, 321, 824-826. http://dx.doi.org/10.1126/science.1157312
- Andersen, E.S., Dong, M., Nielsen, M.M., Jahn, K., Subramani, R., Mamdouh, W., Golas, M.M., Sander, B., Stark, H., Oliveira, C.L.P., Petersen, J.S., Birkedal, V., Besenbacher, F., Gothelf, K.V. and Kjems, J. (2009) Self-Assembly of a Nanoscale DNA Box with a Controllable Lid. Nature, 459, 73-76. http://dx.doi.org/10.1038/nature07971
- Fujibayashi, K., Hariadi, R., Ha Park, S., Winfree, E. and Murata, S. (2008) Toward Reliable Algorithmic Self-Assem- bly of DNA Tiles: A Fixed Width Cellular Automaton Pattern. Nano Letters, 8, 1791-1797. http://dx.doi.org/10.1021/nl0722830
- Zhang, D.Y. (2010) Dynamic DNA Strand Displacement Circuits. Thesis, California Institute of Technology Pasadena, California.
- Zhang, D.Y. and Winfree, E. (2009) Control of DNA Strand Displacement Kinetics Using Toehold Exchange. JACS, 131, 17303-17314. http://dx.doi.org/10.1021/ja906987s
- Zhang, D.Y. and Seelig, G. (2011) Dynamic DNA Nanotechnology Using Strand-Displacement Reactions. Nature Chemistry, 3, 103-113. http://dx.doi.org/10.1038/nchem.957
- Seeman, N.C. (2010) Nanomaterials Based on DNA. Annual Review of Biochemistry, 79, 65-87. http://dx.doi.org/10.1146/annurev-biochem-060308-102244
- Simmel, F.C. (2009) Processive Motion of Bipedal DNA Walkers. ChemPhysChem, 10, 2593-2597. http://dx.doi.org/10.1002/cphc.200900493
- Qian, L. and Winfree, E. (2011) A Simple DNA Gate Motif for Synthesizing Large-Scale Circuits. Journal of the Royal Society Interface, 8, 1281-1297. http://dx.doi.org/10.1098/rsif.2010.0729
- Li, B.L., Ellington, A.D. and Chen, X. (2011) Rational, Modular Adaptation of Enzyme-Free DNA Circuits to Multiple Detection Methods. Nucleic Acids Research, 39, e110. http://dx.doi.org/10.1093/nar/gkr504
- Chen, X., Briggs, N., McLain, J. and Ellington, A.D. (2013) Stacking Nonenzymatic Circuits for High Signal Gain. Proceedings of the National Academy of Sciences of the United States of America, 110, 5386-5391. http://dx.doi.org/10.1073/pnas.1222807110
- Montagne, K., Plasson, R., Sakai, Y., Fujii, T. and Rondelez, Y. (2011) Programming an in Vitro DNA Oscillator Using a Molecular Networking Strategy. Molecular Systems Biology, 7, 466.
- Qian, L. and Winfree, E. (2011) Scaling up Digital Circuit Computation with DNA Strand Displacement Cascades. Science, 332, 1196-1201.
- Qian, L., Winfree, E. and Bruck, J. (2011) Neural Network Computation with DNA Strand Displacement Cascades. Nature, 475, 368-372. http://dx.doi.org/10.1038/nature10262
- Bialek, W. (2012) Biophysics: Searching for Principles. Princeton University Press, Princeton.
- Alon, U. (2007) An Introduction to Systems Biology: Design Principles of Biological Circuits. Chapman & Hall/CRC, Taylor & Francis Group, Boca Raton.
- Yurke, B., Turberfield, A.J., Mills, A.P., Simmel, F.C. and Neumann, J.L. (2000) A DNA-Fuelled Molecular Machine Made of DNA. Nature, 406, 605-608. http://dx.doi.org/10.1038/35020524
- Bishop, J.D. and Klavins, E. (2007) An Improved Autonomous DNA Nanomotor. Nanolet, 7, 2574-2577.
- Tian, Y., He, Y., Chen, Y., Yin, P. and Mao, C.D. (2005) A DNAzyme That Walks Processively and Autonomously along a One-Dimensional Track. Angewandte Chemie International Edition, 44, 4355-4358. http://dx.doi.org/10.1002/anie.200500703
- Lund, K., Manzo, A.J., Dabby, N., Michelotti, N., Buck, A.J., Nangreave, J., Taylor, S., Pei, R.J., Stojanovic, M.N., Walter, N.G., Winfree, E. and Yan, H. (2010) Molecular Robots Guided by Prescriptive Landscapes. Nature, 465, 206- 210. http://dx.doi.org/10.1038/nature09012
- Bath, J., Green, S.J. and Turberfield, A.J. (2005) A Free-Running DNA Motor Powered by a Nicking Enzyme. Angewandte Chemie International Edition, 44, 4358-4361.
- Wickham, S.F.J., Bath, J., Katsuda, Y., Hidaka, M.E.K., Sugiyama, H. and Turberfield, A.J. (2012) A DNA-Based Molecular Motor That Can Navigate a Network of Tracks. Nature Nanotechnology, 7, 169-173. http://dx.doi.org/10.1038/nnano.2011.253
- Wickham, S.F.J., Endo, M., Katsuda, Y., Hidaka, K., Bath, J., Sugiyama, H. and Turberfield, A.J. (2011) Direct Observation of Stepwise Movement of a Synthetic Molecular Transporter. Nature Nanotechnology, 6, 166-169. http://dx.doi.org/10.1038/nnano.2010.284
- Genot, A.J., Zhang, D.Y., Bath, J. and Turberfield, A.J. (2011) Remote Toehold: A Mechanism for Flexible Control of DNA Hybridization Kinetics. Journal of the American Chemical Society, 133, 2177-2182. http://dx.doi.org/10.1021/ja1073239
- Tuberfield, A.J., Mitchell, J.C., Yurke, B., Mills Jr., A.P., Blakey, M.I. and Simmel, F.C. (2003) DNA Fuel for Free- Running Nanomachines. Physical Review Journals, 90, Article ID: 118102. http://dx.doi.org/10.1103/PhysRevLett.90.118102
- Gu, H.Z., Chao, J., Xiao, S.-J. and Seeman, N.C. (2009) Dynamic Patterning Programmed by DNA Tiles Captured on a DNA Origami Substrate. Nature Nanotechnology, 4, 245-249. http://dx.doi.org/10.1038/nnano.2009.5
- Alberti, P. and Mergny, J.L. (2003) DNA Duplex-Quadruplex Exchange as the Basis for a Nanomolecular Machine. Proceedings of the National Academy of Sciences, 100, 1569-1573. http://dx.doi.org/10.1073/pnas.0335459100
- Asanuma, H., Liang, X.G., Nishioka, H., Matsunaga, D., Liu, M.Z. and Komiyama, M. (2007) Synthesis of Azoben- zene-Tethered DNA for Reversible Photo-Regulation of DNA Functions: Hybridization and Transcription. Nature Protocols, 2, 203-212. http://dx.doi.org/10.1038/nprot.2006.465
- Durand, G., Lisi, S., Ravelet, C., Dausse, E., Peyrin, E. and Toulmé, J.J. (2014) Kissing Complex-Based Riboswitches for the Detection of Small Ligands. Angewandte Chemie International Edition, 53, 6942-6945.
- Srinivas, N., Ouldridge, T.E., Sulc, P., Schaeffer, J.M., Yurke, B., Louis, A.A., Doye, J.P.K. and Winfree, E. (2013) On the Biophysics and Kinetics of Toehold-Mediated DNA Strand Displacement. Nucleic Acids Research, 41, 10641- 10658. http://dx.doi.org/10.1093/nar/gkt801
- Astumian, R.D. and Bier, M. (1996) Mechanochemical Coupling of the Motion of Molecular Motors to ATP Hydrolysis. Biophysical Journal, 70, 637-653.
- Prost, J., Chauwin, J.F., Peliti, L. and Ajdari, A. (1994) Asymmetric Pumping of Particles. Physical Review Letters, 72, 2652-2655. http://dx.doi.org/10.1103/PhysRevLett.72.2652
- SantaLucia Jr., J. (1998) A Unified View of Polymer, Dumbbell, and Oligonucleotide DNA Nearest-Neighbor Thermodynamics. Proceedings of the National Academy of Sciences of the United States of America, 95, 1460-1465. http://dx.doi.org/10.1073/pnas.95.4.1460
- Hanggi, P., Talkner, P. and Borkovec, M. (1990) Reaction-Rate Theory: Fifty Years after Kramers. Reviews of Modern Physics, 62, 251-341. http://dx.doi.org/10.1103/RevModPhys.62.251
- Cunha, S., Woldringh, C.L. and Odijk, T. (2005) Restricted Diffusion of DNA Segments within the Isolated Esche- richia coli Nucleoid. Journal of Structural Biology, 150, 226-232. http://dx.doi.org/10.1016/j.jsb.2005.02.004
- Robertson, R.M. and Smith, D.E. (2007) Self Diffusion of Entangled Circular and Linear DNA: Dependence on Length and Concentration. Macromolecules, 40, 3373-3377. http://dx.doi.org/10.1021/ma070051h
- Lifson, S. and Jackson, J.L. (1962) On the Self Diffusion of Ions in Polyelectrolyte Solutions. Journal of Chemical Physics, 36, 2410-2414. http://dx.doi.org/10.1063/1.1732899
- Hunt, A.J., Gittes, F. and Hoard, J. (1994) The Force Exerted by a Single Kinesin Molecule against a Viscous Load. Biophysical Journal, 67, 766-781. http://dx.doi.org/10.1016/S0006-3495(94)80537-5
- Panyutin, I.G. and Hsieh, P. (1994) The Kinetics of Spontaneous DNA Branch Migration. Proceedings of the National Academy of Sciences of the United States of America, 91, 2021-2025. http://dx.doi.org/10.1073/pnas.91.6.2021
- Dennis, C., Fedorov, A., Käs, E., Salomé, L. and Grigoriev, M. (2004) RuvAB-Directed Branch Migration of Indivi- dual Holliday Junctions Is Impeded by Sequence Heterology. The EMBO Journal, 23, 2413-2422. http://dx.doi.org/10.1038/sj.emboj.7600249
- Parmeggiani, A., Jülicher, F., Adjari, A. and Prost, J. (1999) Energy Transduction of Isothermal Ratchets: Generic Aspects and Specific Examples Close to and Far from Equilibrium. Physical Review E, 60, 2127-2140. http://dx.doi.org/10.1103/PhysRevE.60.2127
- Magnasco, M. (1993) Forced Thermal Ratchets. Physical Review Letters, 71, 1477-1481. http://dx.doi.org/10.1103/PhysRevLett.71.1477
- Doering, C.R. and Gadoua, J.C. (1992) Resonant Activation over a Fluctuating Barrier. Physical Review Letters, 69, 2318-2321. http://dx.doi.org/10.1103/PhysRevLett.69.2318
- Hopfield, J.J. (1974) Kinetic Proofreading: A New Mechanism for Reducing Errors in Biosynthetic Processes Requiring High Specificity. Proceedings of the National Academy of Sciences of the United States of America, 71, 4135-4139. http://dx.doi.org/10.1073/pnas.71.10.4135
- Privman, Y. and Frisch, H.L. (1991) Exact Solution of the Diffusion Problem for a Piecewise Linear Barrier. Journal of Chemical Physics, 94, 8216-8219. http://dx.doi.org/10.1063/1.460105
- Samanta, A. and Ghosh, S.K. (1992) Exact Results on Diffusion from a Piecewise Linear Potential Well. Journal of Chemical Physics, 97, 9321-9323. http://dx.doi.org/10.1063/1.463308
- Adjari, A.J. and Prost, J. (1992) Mouvement induit par un potentiel periodique de basse symetrie: Dielectrophorese pulsee. J. Comptes Rendus de l’Académie des Sciences, Paris, 315, 1635-1639.
- Chandran, H., Gopalkrishnan, N., Phillips, A. and Reif, J. (2011) Localized Hybridization Circuits. In: Cardelli, L. and Shih, W., Eds., Proceedings of the 17th International Conference on DNA Computing and Molecular Programming, Pasadena, 19-23 September 2011, 64-83.
- Ruiz, I.M., Arbona, J.M., Lad, A., Aime, J.P. and Elezgaray. J. (Submitted) Localized Seesaw Gates.
Annex 1
Absorbing condition at both end of the device:
The continuity of the probability and current at x = 0 gives:
and the absorbing condition at both end:
From which we obtain:
Residence time and escape rate in an asymmetric piecewise potential well is given by:
Annex 2
Case of a DNA device on origamis: Reflecting condition at the location x = -x1
The potential structure is the same as the one used in Annex 1 with the same type of solutions. The unique difference is the reflecting boundary condition at x = -x1 which writes:
The solution are of the form:
And the residence time:
Annex 3
Other energy landscapes can be chosen that may appear more suitable for DNA device: for instance with left and right slopes proportional to n + m and m respectively, the asymmetry is maintained and the general trend is preserved. In this case the current and reduced residence times are:
- Absorbing conditions at both end:
where the reduced time is scaled at the monomer unit length, with x0 = mu.
- Absorbing at the right side and reflecting at the left side. The reduced time is given by:
NOTES
*Corresponding author.
2Note that m might not be only referred to the length of the output strand, but can also account for a length of the invader that has a common sequence shorter than the output one. In this case, for a given toe hold strength the efficiency of the invader is reduced lowering the asymptotic plateau height of the effective bimolecular rate [9] [10] .
























































