Materials Sciences and Applications
Vol.5 No.5(2014), Article ID:44802,8 pages DOI:10.4236/msa.2014.55035
Transport Properties of AgInSe2 Crystals
Hamdy T. Shaban1,2*, Melaad K. Gergs2
1Physics Department, College of Science and Arts, Najran University, Najran, KSA
2Physics Department, Faculty of Science, South Valley University, Qena, Egypt
Email: *htsh2@Yahoo.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 4 January 2014; revised 18 February 2014; accepted 7 March 2014
ABSTRACT
AgInSe2 crystals were grown by Bridgman technique. The crystals were identified structurally by X-ray diffraction technique. Measurements of electrical conductivity and Hall effect were performed in the temperature range (138 K - 434 K) and (220 K - 488 K) for thermoelectric power measurements. From these measurements, many physical parameters were determined. The energy gap was calculated to be 1.24 eV. The conductivity type was found to be n-type. Crystallite size (D) of the obtained AgInSe2 crystals was calculated to be 70 nm. The lattice parameters for the prepared crystals were a = 6.0938 Å and c = 11.7775 Å.
Keywords:Semiconductors, Crystal Growth, X-Ray Diffraction, Transport Properties

1. Introduction
The Ag-In-Se ternary semiconductors have great potential for the photovoltaic applications especially for deposition as an absorber layer for solar cells as AIBIIIC2VI-type chalcopyrite ternary semiconductor materials [1] -[6] . Hall measurement of AgInSe2 crystals was carried out in a low temperature range from 100 to 300 K [7] . The electrical conductivity and thermoelectric power of AgInSe2 have been investigated as a function of temperature from 420˚C to 950˚C [8] . Thermoelectric properties of a wide-band gap chalcopyrite compound AgInSe2 were studied. They report the enhanced thermoelectric performance of AgInSe2 compared to In2Se3 [9] . Structural and electrical characterization of AgInSe2 crystals grown by hot-press method was studied. It was found that the largest grain size was approximately 90 nm. The crystals had a resistivity of 2.2 W cm, a carrier concentration of 4.2 × 1016 cm−3 and a mobility of 70 cm2V−1s−1 obtained by Hall measurement at RT [10] . In the present work we have studied the electrical conductivity, Hall effect and thermoelectric power measurements in a wider range of high and low temperatures. Also, the structural studies were performed. Our investigation aimed to preparation of AgInSe2 by a Bridgman method and collecting much more information about the semiconductor parameters of this compound.
2. Experimental Procedures
2.1. Growth and Characterization
The crystals of AgInSe2 were grown by Bridgman technique. According to this technique, the samples have been prepared by the direct melting of the starting materials (Ag, In and Se) in quartz ampoule which was sealed under vacuum of about 10−4 Torr. The silica ampoule and its charge were mounted in the first zone of a threezone tube furnace. The temperature in the first zone was higher than the melting point, and then the temperature was kept about 24 h for complete melting and mixing of the starting materials. The temperature of the middle zone of the furnace was 1073 K corresponding to the crystallization temperature of AgInSe2 as reported in the phase diagram [11] . When the ampoule and the melt were gradually entered the third zone, solidification occurred since the temperature was adjusted to be less than the melting point.
2.2. Electrical Conductivity and Hall Effect Measurements
Samples of rectangular form of 7.4 × 2.8 × 0.8 mm3 dimensions were used for performing the electrical conductivity and Hall coefficient measurements. In this way, the length of the sample was adjusted to be nearly 3 times its width to avoid Hall voltage drop [12] . A pyrex cryostat was used for adjusting the low temperature and high temperature [13] . The cryostat, which contains the crystal, was evacuated (10−4 Torr) to avoid water vapour condensation or crystal oxidation. In this experiment, we used a very sensitive potentiometer (UJ33E mark) and an electromagnet (Oxford N 177 type) which generates 5000 G.
2.3. Thermoelectric Power Measurements
For thermoelectric power measurements, the investigated sample was adjusted to be 5 mm in diameter and 10 mm in length by polishing processes. The thermoelectric power was measured by using a pressure contact sample holder with a heater and a heat sink to obtain a temperature difference between the opposed surfaces of the sample (≈3˚C). Also, an evacuated calorimeter (10−3 Torr) was used to protect the sample from oxidation and water vapour condensation at high and low temperatures, respectively. Simultaneous measurements of temperature and thermovoltage were carried out to increase the accuracy of the measurements.
3. Results and Discussion
3.1. Structural Analysis
Figure 1 depicts the X-ray diffractogram for the prepared AgInSe2 crystals. The powder XRD analysis confirms the synthesis of tetragonal AgInSe2 with prominent peaks from (112), (103), (200), (105), (220), (204) (3121), (116), (400), (322), (316) and (424) planes. The lattice parameters a and c of grown crystals AgInSe2 have been calculated by plotting the lattice parameters, ahkl and chkl (calculated from the Bragg’s Law of the main peaks) against an extrapolation function:
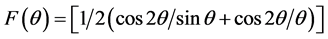
Figure 2 shows the relation between the lattice a and F(q). The estimated values of lattice parameters of AgInSe2 tetragonal phases are a = 6.0938 Å and c = 11.7775 Å [14] . The Crystallite size (D) of the obtained AgInSe2 crystals was 70 nm according to the Debye-Scherrer’s formula from the full width at half-maximum (FWHM) b of the peaks expressed in radians [15]
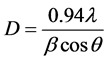 (1)
(1)
where l is 1.540598 Å for CuKα and q is the Bragg angle.
3.2. Electrical Conductivity and Hall Measurements
Figure 3 shows the temperature dependence of electrical conductivity s for AgInSe2 crystals. In the low tem-
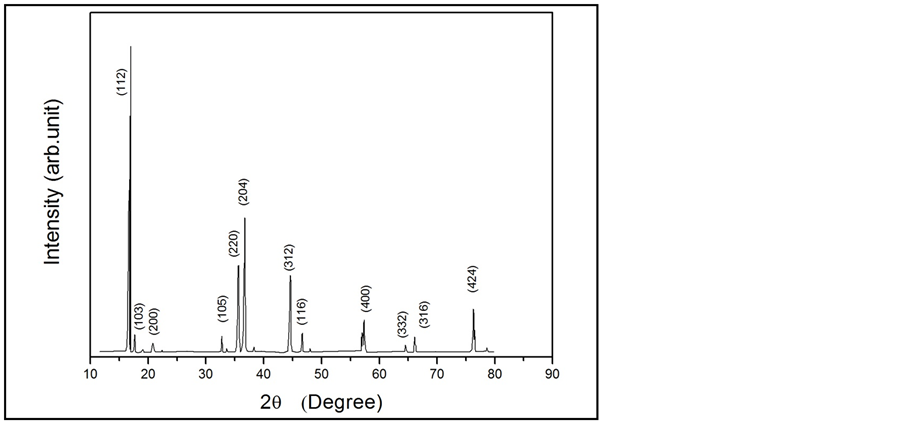
Figure 1. X-ray diffraction for AgInSe2.

Figure 2. The relation between the lattice a and F(q).

Figure 3. Temperature dependence of s for AgInSes.
perature range (138 - 273 K), representing the extrinsic region, s increases slowly with temperature as a result of the transition of the carriers from the impurity level to the conduction band. The activation energy DEd was found to be 0.06 eV as computed in this range. In the same curve, one can notice that the transition region lies between 273 and 330 K. Above 330 K, the intrinsic conduction region begins where s increases. This reveals that both electrons and holes contribute to the conduction at this high temperature range. The temperature dependence in the intrinsic conduction follows the relation:
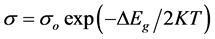 (2)
(2)
where σo is the pre-exponential factor and DEg is the energy gap. From Figure 3, DEg was calculated from the slope of the curve, and found to be 1.24 eV, which is closd to the value that was published before [16] . Meanwhile, the room temperature conductivity was 0.48 W−1cm−1.
Figure 4 shows the relation between Hall coefficient RH and 103/T. This curve is divided into two regions: The first part of low temperatures, RH begins to increase as the temperature increases until 330 K. This region indicated the extrinsic region. The second region above 330 K, RH decreases as the temperature increases. This region indicated the intrinsic region. The Hall coefficient at room temperature is evaluated as 1054 cm3/C.
Figure 5 shows the temperature dependence on the Hall mobility μH (where ). From this curve, we can distinguish two regions. In the first region of low temperatures (T < 330 K), μH increases with temperature following the relation μαT2.6. Such behavior is the characteristic of a scattering mechanism of the charge carriers with ionized impurities. While the second region of the high temperatures (T > 330 K), mobility decreases with increasing temperature according to a power relation,
). From this curve, we can distinguish two regions. In the first region of low temperatures (T < 330 K), μH increases with temperature following the relation μαT2.6. Such behavior is the characteristic of a scattering mechanism of the charge carriers with ionized impurities. While the second region of the high temperatures (T > 330 K), mobility decreases with increasing temperature according to a power relation, 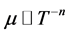 where n = 10. This may lead to the assumption that the carrier scattering mechanism is due to the interaction between charge carriers and phonons which is dominant. At room temperature, Hall mobility equals 510 cm2/Vs. Figure 6 shows the carrier concentration as a function of temperature. It is observed from the curve that the temperature increases monotonically with concentration. Within the intrinsic region of conduction, the following relation can be applied to describe the temperature dependence on the charge carrier concentration ni:
where n = 10. This may lead to the assumption that the carrier scattering mechanism is due to the interaction between charge carriers and phonons which is dominant. At room temperature, Hall mobility equals 510 cm2/Vs. Figure 6 shows the carrier concentration as a function of temperature. It is observed from the curve that the temperature increases monotonically with concentration. Within the intrinsic region of conduction, the following relation can be applied to describe the temperature dependence on the charge carrier concentration ni:
 (3)
(3)
The calculated energy gap from this relation equals 1.24 eV which is in agreement with that previously obtained from the conductivity work. Finally, the charge carriers concentration at room temperature amounts 1.5 × 1016 cm−3 for the AgInSe2 crystals.
3.3. Thermoelectric Power Measurement
The thermoelectric power (TEP) measurements of AgInSe2 were carried out as a complementary part to the electrical conductivity and Hall effect. The relation between thermoelectric power α and the temperature is depicted in Figure 7. From this figure, we can see that α increases with temperature up to its maximum value (709 μV/K ) at a temperature 325 K. Above 325 K, α decreases until about 488 K. The growth of α with T (between 220 and 325 K) is due to the thermal activation of the charge carriers. At T = 325 K (the maximum value of α) the intrinsic conduction appears. The decrease of a above 325 K is due to the compensation process which takes place in this range of temperature. TEP of the AgInSe2 sample has a negative sign over the entire considered temperature range. The value of thermoelectric power at room temperature is 146 αV/K [17] . The behavior of thermoelectric power with temperature in the intrinsic region can be described by the following equation [18]
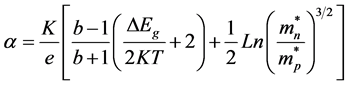 (4)
(4)
where b is the ratio of electron and hole mobility , DEg is the energy gap, K is the Boltzman constant and
, DEg is the energy gap, K is the Boltzman constant and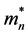 ,
, 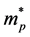 are the effective masses of electrons and holes, respectively. Taking into consideration the value of
are the effective masses of electrons and holes, respectively. Taking into consideration the value of  eV(as obtained from the electrical conductivity measurements in the same range of T), the ratio of the electron and hole mobility was calculated from the slope of the line in the high temperature range of Figure 7 and was found to be 1.71. By considering the value of μp = 510 cm2/Vs which was obtained from the Hall measurements data, the value of μp was estimated to be 235 cm2/Vs. Meanwhile, the ratio
eV(as obtained from the electrical conductivity measurements in the same range of T), the ratio of the electron and hole mobility was calculated from the slope of the line in the high temperature range of Figure 7 and was found to be 1.71. By considering the value of μp = 510 cm2/Vs which was obtained from the Hall measurements data, the value of μp was estimated to be 235 cm2/Vs. Meanwhile, the ratio 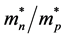 was also calculated from the intercept of the curve with α-axis and was found to be 0.01.
was also calculated from the intercept of the curve with α-axis and was found to be 0.01.
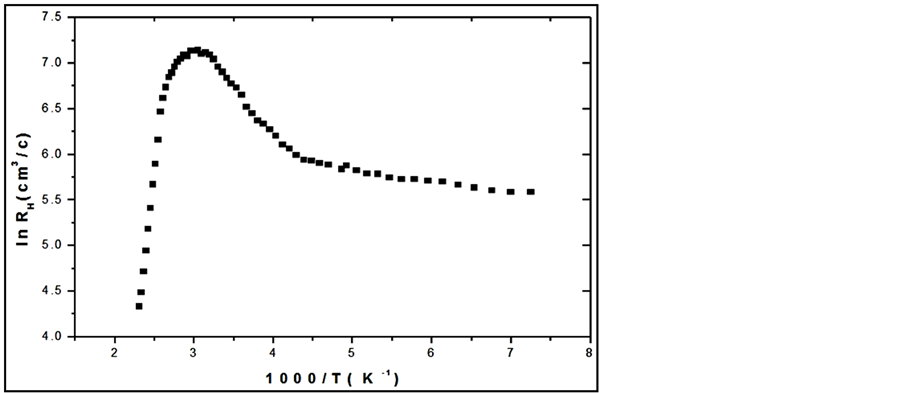
Figure 4. Relation between Hall coefficient and 1000/ T for AgInSe2.
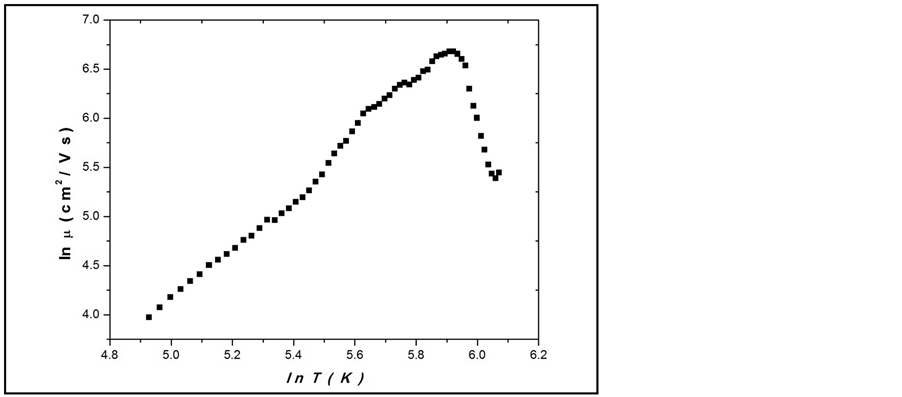
Figure 5. Behavour of μ as a function of temperature for AgInSe2.
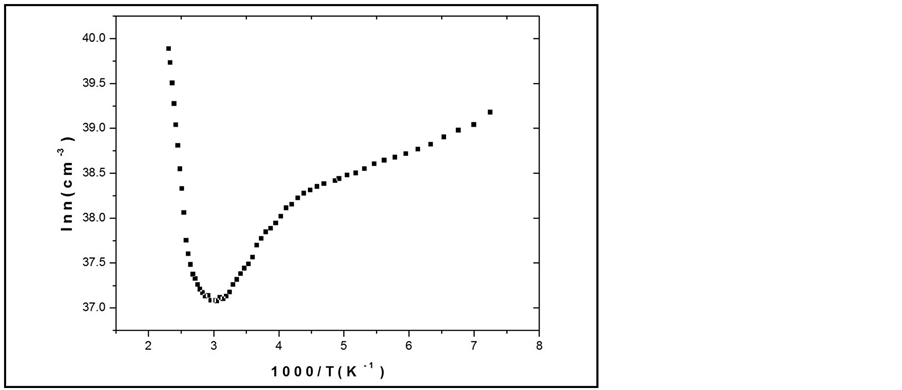
Figure 6. Variegation of carrier concentration with temperature for AgInSe2.
Another important equation was employed in the extrinsic region [19] , is as follows:
 (5)
(5)
According to this equation the relation between α and lnT was drawn. Then from the intercept of the line (in the impurity region) with the α-axis, we got  = 1 × 10−31 kg. Taking into account the ratio previously obtained from Figure 7, we evaluated
= 1 × 10−31 kg. Taking into account the ratio previously obtained from Figure 7, we evaluated  as 1 × 10−29 kg. The value of the relaxation time for electrons was 3.18 × 10−10 sec. It was calculated according to the equation
as 1 × 10−29 kg. The value of the relaxation time for electrons was 3.18 × 10−10 sec. It was calculated according to the equation  while for holes it is 1.88 × 10−8 s. Furthermore, the diffusion constants for electrons and holes were calculated and found to be Dn = 13.19 cm2/s and Dp = 7.45 cm2/s, respectively (where
while for holes it is 1.88 × 10−8 s. Furthermore, the diffusion constants for electrons and holes were calculated and found to be Dn = 13.19 cm2/s and Dp = 7.45 cm2/s, respectively (where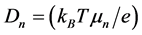 . The diffusion length Ln and Lp were also calculated and found to be 6.47 × 10−5 cm and 3.74 × 10−4 cm for electrons and holes, respectively (where
. The diffusion length Ln and Lp were also calculated and found to be 6.47 × 10−5 cm and 3.74 × 10−4 cm for electrons and holes, respectively (where ).
).
Figure 8 shows the dependence of thermoelectric power on the charge carriers concentration n which follows the equation [20]
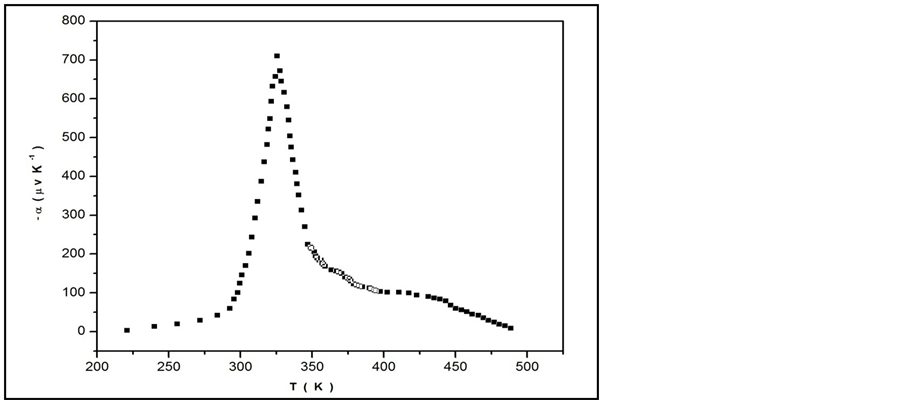
Figure 7. Relation between thermoelectric power (α) and 1000/T for AgInSe2.
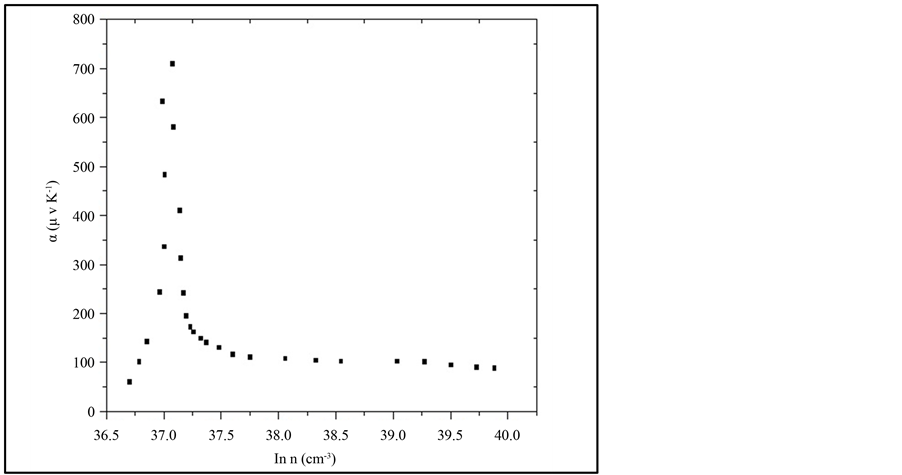
Figure 8. Variegation of the thermoelectric power (α) with (n) for AgInSe2.
 (6)
(6)
where A is a constant depending on the scattering mechanisms.
The similar behavior in Figure 7 and Figure 8 suggests that the variation of α may be to the variation of carrier concentration with temperature.
4. Conclusion
AgInSe2 crystals were grown by Bridgman technique. The results of investigations were carried out to determine the structural, electrical and thermoelectric power properties of the obtained AgInSe2 crystals. From these measurements, many physical parameters were estimated. Crystallite size (D) of the AgInSe2 crystals was calculated to be 70 nm. The estimated values of lattice parameters of AgInSe2 are a = 6.0938 Å and c = 11.7775Å. The energy gap was found to be 1.24 eV. Conductivity type was found to be n-type.
Acknowledgements
The authors acknowledge the Deanship of Scientific Research, Najran University, Najran, Saudi Arabia, for providing financial support (project no. NU 32/11).
References
- Santos Kumar, M.C. and Praveen, B. (2004) Formation and Properties of AgInSe2 Thin Films by Co-Evaporation. Vacuum, 72, 369-378. http://dx.doi.org/10.1016/j.vacuum.2003.09.008
- Mobarak, M., Shaban, H.T. and Elhady, A.F. (2008) Electrical and Thermoelectric Properties of CuInS2 Single Crystals. Materials Chemistry and Physics, 109, 287-290. http://dx.doi.org/10.1016/j.matchemphys.2007.11.025
- Colakoglu, T. and Parlak, M. (2008) Structural Characterization of Polycrystalline Ag-In-Se Thin Films Deposited by E-Beam Technique. Applied Surface Science, 254, 1569-1577. http://dx.doi.org/10.1016/j.apsusc.2007.07.092
- Kishigui, K., Abe, K., et al., (2008) Study of Steady-State Photoluminescence of AgInSe2 Crystals. Thin Solid Films, 517, 1445-1448. http://dx.doi.org/10.1016/j.tsf.2008.09.014
- Al-Agel, F.A. and Mahmoud, W.E. (2012) Synthesis and Characterization of AIS Chalcopyrite Thin Films for Solar Cell Applications. Materials Letters, 82, 82-84. http://dx.doi.org/10.1016/j.matlet.2012.05.065
- Maihmoud, F.A. and Sayed, N.H. (2011) Preparation and Chartacterization of AgInSe2 Thin Films. Chalcogenide Letters, 8, 595-600.
- Yoshinoa, K., et al., (2001) Optical and Electrical Properties of AgIn(SSe)2 Crystals. Physica B, 302-303, 349-356. http://dx.doi.org/10.1016/S0921-4526(01)00453-7
- Abdelghany, A. (1995) Electrical Conductivity and Thermoelectric Power of AgInSe2 in the Solid and Liquid States. Applied Physics A, 60, 77-79. http://dx.doi.org/10.1007/BF01577617
- Ying, P.Z., et al., (2012) Thermoelectric Properties of a Wide-Gap Chalcopyrite Compound AgInSe2. Key Enginering Materials, 519, 188-192. http://dx.doi.org/10.4028/www.scientific.net/KEM.519.188
- Yoshino, K., et al., (2008) Structural and Electrical Characterization of AgInSe2 Crystals Grown by Hot-Press Method. Journal of Physics: Conference Series, 100, 042042.
- Mustafa, H., Hunter, D., Pradhan, A.K., Roy, U.N., Cuib, Y. and Burger, A. (2007) Synthesis and Characterization of AgInSe2 for Application in Thin Film Solar Cells. Thin Solid Films, 515, 7001-7004. http://dx.doi.org/10.1016/j.tsf.2007.02.054
- Isenberg, L., Russel, B. and Greene, R.F. (1948) Improved Method for Measuring Hall Coefficients. Review of Scientific Instruments, 19, 685. http://dx.doi.org/10.1063/1.1741078
- Hussein, S.A. (1989) Temperature Dependences of the Electrical Conductivity and Hall Coefficient of Indium Telluride Single Crystals. Crystal Research and Technology, 24, 635. http://dx.doi.org/10.1002/crat.2170240616
- Benoit, P., Charpin, P., Lesueur, R. and Djega-Mariadassou, C. (1980) Crystal Structure of Chalcopyrite AgInSe2. Japanese Journal of Applied Physics, 19, 85-88. http://dx.doi.org/10.7567/JJAPS.19S3.85
- Ebnalwaled, A.A. (2009) Evolution of Growth and Enhancement in Power Factor of InSb Bulk Crystal. Journal of Crystal Growth, 311, 4385-4390. http://dx.doi.org/10.1016/j.jcrysgro.2009.07.040
- Tell, B. and Kasper, H.M. (1974) Electrical properties of AgInSe2. Journal of Applied Physics, 45, 5367. http://dx.doi.org/10.1063/1.1663244
- Shay, J.L. and Wernick, J.H. (1975). Ternary Chalcopyrite Semiconductors, Pergamon NY.
- Johnson, V.A. and Lark-Horov, K. (1953) Theory of Thermoelectric Power in Semiconductors with Applications to Germanium. Physical Review, 92, 226-232. http://dx.doi.org/10.1103/PhysRev.92.226
- Wilson, H. (1953). Theory of Metals, 2nd A Edition, Cambridge University Press, Cambridge.
NOTES

*Corresponding author.

