ABSTRACT

I report the reason why Tensor satisfying Binary Law has relations toward physics in this article. Q: The n th-order covariant derivative of the Vector 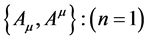satisfying Binary Law. R: The n th-order covariant derivative of the Vector 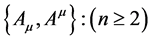satisfying Binary Law. I have reported in other articles about Q. I report R in this article. I obtained the following results in this. I got the conclusion that derived function became 0. The derived function becoming 0 in the n th-order covariant derivative of the covariant vector 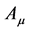here in the case of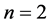. Similarly, in the n th-order covariant derivative of the contravariant vector 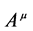in the case of.

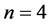Keywords:

Tensor Covariant Derivative

1. Introduction

Definition 1

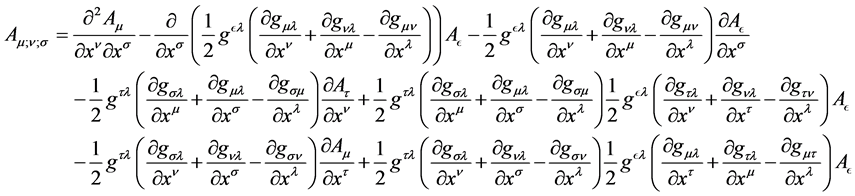
is established [1] .

Definition 2 is established [2] .

I named 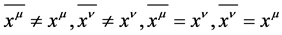“Binary Law” [2] .

Definition 3 If 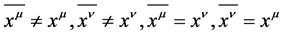is established; 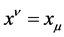is established [2] .

Definition 4 If 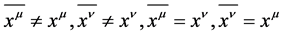is established; 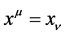is established [2] .

Definition 5 If 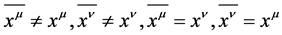is established; is established [2] .

Definition 6 If 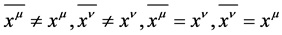is established; is established [2] .

Definition 7 If all coordinate systems 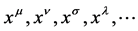satisfies

, all coordinate systems shifts to only two of [2] .

Definition 8

is established [3] .

Definition 9 is established [4] .

Definition 10, is establishment [3] .

Definition 11

is established [3] .

Definition 12

is established [3] .

Definition 13 For every coordinate systems, there is no immediate reason for preferring certain systems of co-ordinates to others.

Definition 14 The physical law is invariable for all coordinate systems [1] .

Definition 15 “All coordinate systems satisfies Definision 13” is established if Definision 14 is established.

Definition 16 Definision 14 is established if “The physical law is described in Tensor” is established [1] .

Definition 17 “All coordinate systems satisfies Definision 13” is established if “All coordinate systems satisfies Binary Law” is established [2] .

A.Einstein required establishment of Definision 14 approximately 100 years ago [1] . Furthermore, he required establishment of “The physical law is described in Tensor” based on Definision 16 [1] . However, A. Einstein does not mention Definision 15 at all [1] . I get the conclusion that “All coordinate systems satisfies Definision 13” must be established if Definision 14 is established according to Definision 15. On the other hand, I got that Definision 17 was established [2] . And I got the conclusion that must require establishment of “All coordinate systems satisfies Binary Law” if I required establishment of Definision 14 by Definision 17. Scalar and Vector have already satisfied these two demands here [2] . In other words, we can use Scalar and Vector to express a physical law. Therefore, I do not mention it for Scalar and Vector. I researched it about the Tensor which had not yet satisfied Binary Law in this article. The first purpose of this article is to rewrite the Tensor which does not satisfy Binary Law in Tensor satisfying Binary Law. Then, the second purpose is to find out the property from Tensor satisfying Binary Law.

2. About Property of Tensor Satisfying Binary Law: The Second, Third, Fourth-Order Covariant Derivative of the Vector

Proposition 1 If is established,

is established.

Proof: I get

(1)

from Definision 10 if all coordinate systems satisfies Definision 2. I get

(2)

from Definision 1 if all coordinate systems satisfies Definision 2. By the way, we cannot handle (2) according to Definision 7. I simplify (2) here and get

(3)

However, (3) can rewrite

(4)

if and of (3) are changeable to or each. Because index doesn’t exist at all in the third term of the right side of (3), I can change dummy index of (3) to dummy index. Furthermore, (4) can rewrite

(5)

Because index doesn’t exist at all in the second term of the right side of (4), I can change dummy index of (4) to dummy index. And we can

handle (5) according to Definision 7. The possible rewrite by or of is

(6)

(7)

(8)

according to Definision 4, Definision 6. Because three covariant Vector of the same index exists in one term, I don’t handle (6). Two sets are dummy index among three same index in (7), (8). Therefore, we must rewrite (2) to

(9)

(10)

(11)

by using Definision 4, Definision 6 with considering (7), (8). I get

(12)

in consideration of establishment of from (9), (10) here. I get

(13)

in consideration of (1) for (12). And I get

(14)

from (13). I get

(15)

from in consideration of Definision 4 here. I get

(16)

from (14), (15). Therefore, I get

(17)

(18)

(19)

from (9), (10), (11) in consideration of (1), (13), (16). And we can rewrite (17), (18), (19) by using Definision 4, Definision 6 for

(20)

Because the second, third, term of the right side of (17), (18), (19) does not exist here, we may adopt (17), (18), (19) and (20) description form of which. Furthermore, I rewrite (20) by Definision 4 and get

(21)

in consideration of Proposition 2. And I rewrite (21) by Definision 4 and get

(22)

―End Proof―

Because (22) is established, I decide not to handle the third-order, covariant derivative of the covariant Vector.

Proposition 2 If is established, is established.

Proof: I get

(23)

from Definision 8 if all coordinate systems satisfies Definision 2. I get

(24)

from, Definision 3. I get

(25)

from (24). I get

(26)

from (25), Definision 4. Therefore, I get

(27)

from (23), (26). I get

(28)

from Definision 9 if all coordinate systems satisfies Definision 2. I get

(29)

from, Definision 3 if all coordinate systems satisfies Definision 2. I get

(30)

from (29). I get

(31)

from (28), (30). I get

(32)

from covariant derivative of (31). I get from (27), (32).

―End Proof―

Proposition 3 If is established,

is established.

Proof: I get

(33)

(34)

from Definision 11 if all coordinate systems satisfies Definision 2. By the way, we cannot handle (33), (34) according to Definision 7. I simplify (33) here and get

(35)

However, (35) can rewrite

(36)

if and of (35) are changeable to or each. Because index doesn’t exist at all in the third term of the right side of (35), I can change dummy index of (35) to dummy index. Furthermore, (36) can rewrite

(37)

Because index doesn’t exist at all in the second term of the right side of (36), I can change dummy index of (36) to dummy index. And we can

handle (37) according to Definision 7. The possible rewrite by or of is

(38)

(39)

(40)

according to Definision 4, Definision 6. Because three contravariant Vector of the same index exists in one term, I don’t handle (40). Two sets are dummy index among three same index in (38), (39). Therefore, we must rewrite (33) to

(41)

(42)

(43)

by using Definision 4, Definision 6 with considering (38), (39). I get

(44)

in consideration of establishment of from (42), (43) here. I get

(45)

in consideration of (1) for (44). Therefore, I get

(46)

(47)

(48)

from (41), (42), (43) in consideration of (1), (45). And we can rewrite (46), (47), (48) by using Definision 4, Definision 6 for

(49)

Because the second, third, term of the right side of (46), (47), (48) does not exist here, we may adopt (46), (47), (48) and (49) description form of which. Similarly, we must rewrite (34) to

(50)

(51)

(52)

by using Definision 4, Definision 6 with considering (38), (39). Because (51) includes here, I don’t handle (51). Therefore, I get (46), (48) from (50), (52) in consideration of (1).

―End Proof―

Proposition 4 If is established,

is established.

Proof: I get

(53)

(54)

from Definision 12 if all coordinate systems satisfies Definision 2. By the way, we cannot handle (53), (54) according to Definision 7. I simplify (53) here and get

(55)

However, (55) can rewrite

(56)

if and of (55) are changeable to or each. Because index doesn’t exist at all in the fourth term of the right side of (55), I can change dummy index of (55) to dummy index. Furthermore, (56) can rewrite

(57)

Because index doesn’t exist at all in the third term of the right side of (56), I can change dummy index of (56) to dummy index. Furthermore, (56) can rewrite

(58)

Because index doesn’t exist at all in the second term of the right side of (57), I can change dummy index of (57) to dummy index. And we can

handle (58) according to Definision 7. The possible rewrite by or of is

(59)

(60)

(61)

(62)

according to Definision 4, Definision 6. Because two covariant Vector of the same index exists in one term, I don’t handle (59). Because two contravariant Vector of the same index exists in one term, I don’t handle (61). Because four contravariant Vector of the same index exists in one term, I don’t handle (62). Therefore, we must rewrite (53) to

(63)

(64)

(65)

by using Definision 4, Definision 6 with considering (60). I get

(66)

in consideration of establishment of from (64), (65) here. I get

(67)

in consideration of (1) for (66). Therefore, I get

(68)

(69)

(70)

from (63), (64), (65) in consideration of (1), (67). And we can rewrite (68), (69), (70) by using Definision 4, Definision 6 for

(71)

Because the second, third, term of the right side of (68), (69), (70) does not exist here, we may adopt (68), (69), (70) and (71) description form of which. Similarly, we must rewrite (54) to

(72)

(73)

(74)

by using Definision 4, Definision 6 with considering (60). Because (72) includes here, I don’t handle (72). I get

(75)

in consideration of establishment of from (73), (74) here. I get

(76)

in consideration of (1) for (75). Therefore, I get (69), (70) from (73), (74) in consideration of (1), (76).

―End Proof―

Proposition 5 If is established,

is established.

Proof: I get

(77)

from if all coordinate systems satisfies Definision 2. And I get

(78)

from (77), Proposition 2, Proposition 4.

―End Proof―

Because (78) is established, I decide not to handle the fifth-order, covariant derivative of the contravariant Vector.

Proposition 6 If is established,

is established.

Proof: I get

(79)

from (71) if a dimensional number is 2. I get

(80)

from (79). And I get

(81)

from (80). I get

(82)

from (81). I get

(83)

from (82), Definision 5. And I get

(84)

from (83). I get

(85)

from (84). And I get

(86)

from (85).

―End Proof―

3. Discussion

About Proposition 1

In (22), we can handle as Tensor similarly. Furthermore,

is established. I do not handle the derived function of a higher order because derived function is already 0.

About Proposition 3

In (49), we can handle as Tensor similarly.

About Proposition 4

In (71), we can handle as Tensor similarly.

Furthermore, is established.

About Proposition 5

In (78), is established. I do not handle the derived function of a higher order because derived function is already 0.

About Proposition 6

If is established in (71), can’t have a wave-like property. However, has a wave-like property if is established in (71).

These remind me of the matter wave in the quantum theory.

Cite this paper

Ichidayama, K. (2017) Property of Tensor Satisfying Binary Law. Journal of Modern Physics, 8, 944-963. https://doi.org/10.4236/jmp.2017.86060

References