ABSTRACT

The unattainability of the absolute zero of temperature is proved by using Carnot’s theorem. Hence this unattainability is distinct from the Planck-Fer- mi statement of the Third Law of Thermodynamics that the entropy vanishes at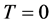. It is shown that the isothermal compressibility 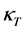is in general larger than the adiabatic compressibility 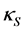and the difference 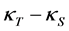vanishes in the low temperature limit.

Keywords:

Nernst’s Theorem, Carnot’s Theorem, Adiabatic Compressibility, Isothermal Compressibility: The Third Law of Thermodynamics

1. Introduction

Fermi in his book [1] stated for the Third Law that the entropy S of any system approaches zero in the zero temperature limit:

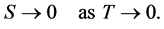(1)

This form was proposed earlier by Planck, and will be called Planck-Fermi’s statement. Reif in his book [2] took a view that thermodynamics and statistical mechanics should be studied jointly by introducing Boltzmann’s connection between the entropy S and the number of microstates 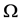compatible with a set of macroscopic descriptors E, V, and N:

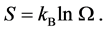(2)

Nernst’s theorem (the third law) was expressed as

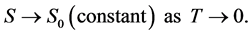(3)

The difference between the two statements is due to the zero point motion arising from the Heisenberg’s uncertainty principle. Neither disorder nor dissipation can be generated by the zero-point motion. Quantum statistics will play a roll.

Pauli, in his book [3] , showed that the unattainability of absolute zero can be derived from Planck-Fermi’s statement by considering Carnot’s cycles. We shall show in the present work that the unattainability can be derived by using Carnot’s theorem (the second law).

The heat absorbed by a body is denoted by Q. The heat capacity C is defined by

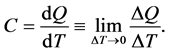(4)

This molar heat at constant volume, 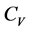, and that at constant pressure, 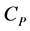, are defined by

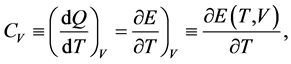(5)

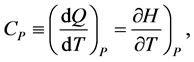(6)

where E and 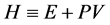are the internal energy and the enthalpy, respectively. We assume that all thermodynamic functions for a one-component system are analytic within each domain of the gas, liquid and solid (phases). The thermodynamic functions are singular on the phase boundary. The body temperature should rise when heat is supplied. Hence the heat capacity should be non-negative. The body volume should become smaller when a pressure is applied from outside. Hence the compressibility should be positive.

Pauli showed in his book [3] that

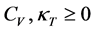(7)

by using the increasing entropy principle. The difference between 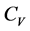and 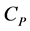is given by

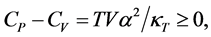(8)

where

(9)

is the coefficient of thermal expansion and

(10)

is the isothermal compressibility.

We see from Equation (8),

(11)

The adiabatic compressibility is defined by

(12)

Both and are positive. Since the restoring forces are different the compressibility are distinct in the different phases.

We shall show newly in Section 3 that

(13)

2. The Unattainnability of the Absolute Zero

Let us consider a gas. In the Carnot cycle shown in Figure 1 the heat are absorbed (emmitted) on isothermal lines AB (CD) and the cycle is closed on adiabatic lines BC (DA). Carnot’s equation is given by

(14)

The efficiency of the Carnot’s engine is

(15)

where W is the work produced. According to Carnot’s theorem, no engine working between two temperatures can have a hgher efficiency than the Carnot engine. Thus the Carnot efficiency represents the highest possible efficiency for any engine working between and,.

In the Carnot cycle operated in the reverse direction an amount of heat is extracted from the low temperature reservoir. We may look at it as an ideal refrigirator if we regard the high temperature as the environment temperature. By solving Carnot’s equations Equations (14) and (15) we obtain

(16)

This expression indicates that the work W needed to extract a fixed amount of heat from a body at becomes greater as decreases. Accordingly, the operating cost of a refrigerator is higher if the temperature is set lower. Furthermore, if the temperature were to approach absolute zero, the work W needed will approach infinity. This means that attaining absolute zero by any means is impossible. All actual refrigerating machines must involve irreversible

processes which add an extra heat to the right-hand side of Equation (16).

3. Isothermal and Adiabatic Compressibilities Approach Each Other in the Low Temperature Limit

After straightforward calculations which are outlined in Appendix, we obtain

(17)

Using this we obtain

(18)

The last inequality follows from inequalities in Equation (8). Hence the iso- thermal compressibility is in general larger than the adiabatic compressi- bility. Using Equation (11), we then obtain

(19)

Cite this paper

McNabb III, J.R., Fujita, S. and Suzuki, A. (2017) On Nernst’s Theorem and Compressibilities. Journal of Modern Physics, 8, 839-843. https://doi.org/10.4236/jmp.2017.85052

References

Appendix: Derivation of Equation (17)

Pressure P, volume V and temperature T are interrelated by the equation of state. If the variables are interrelated, then the differentials are related as

(20)

From this we obtain

(21)

(22)

Using Equations (12) and (22), we obtain

(23)

If we regard S as a function of and T as a function of:

, we get

(24)

Similarly, we obtain

(25)

Using Equations (10), (23)-(25), we obtain

(26)

Dividing this by we obtain Equation (17).