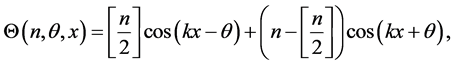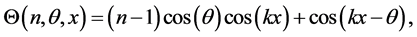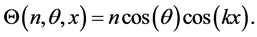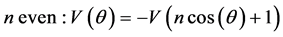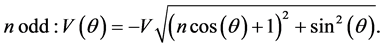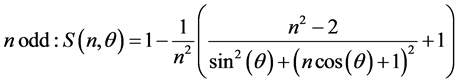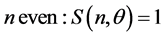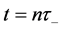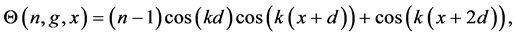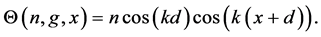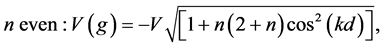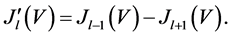Journal of Modern Physics
Vol.07 No.15(2016), Article ID:71893,20 pages
10.4236/jmp.2016.715180
Theory of a Kaptiza-Dirac Interferometer with Cold Trapped Atoms
Ruolei Cheng1, Tianchen He2, Weidong Li1, Augusto Smerzi3
1Institute of Theoretical Physics and Department of Physics, Shanxi University, Taiyuan, China
2Department of Physics, Taiyuan Normal University, Taiyuan, China
3QSTAR, INO-CNR and LENS, Firenze, Italy

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: October 13, 2016; Accepted: November 7, 2016; Published: November 10, 2016
ABSTRACT
We theoretically analyse a multi-modes atomic interferometer consisting of a sequence of Kapitza-Dirac pulses (KD) applied to cold atoms trapped in a harmonic trap. The pulses spatially split the atomic wave-functions while the harmonic trap coherently recombines all modes by acting as a coherent spatial mirror. The phase shifts accumulated among different KD pulses are estimated by measuring the number of atoms in each output mode or by fitting the density profile. The sensitivity is rigorously calculated by the Fisher information and the Cramér-Rao lower bound. We predict, with typical experimental parameters, a temperature independent sensitivity which, in the case of the measurement of the gravitational constant g can significantly exceed the sensitivity of current atomic interferometers.
Keywords:
Atom Interferometry, Kapitza-Dirac Pulse, Dynamics, Gravitational Acceleration Constant, Sensitivity, Noise and Decoherence

1. Introduction
The goal of interferometry is to estimate the unknown value of a phase shift. The phase shift can arise because of a difference in length among two interferometric arms, as in the first optical Michelson-Morley probing the existence of aether or in LIGO and VIRGO gravitational wave detectors [1] . Phase shifts can also be the consequence of a supersonic airflow perturbing one optical path, as in the first Mach-Zehnder [2] , or inertial forces as in Sagnac [3] . Interferometers are among the most exquisite measurement devices and since their first realisations have played a central role on pushing the frontier of science.
Since the last decade, matter wave interferometers have progressively become very competitive when measuring electromagnetic or inertial forces. In particular, atom interferometers [4] [5] have been exploited to obtain the most accurate estimate of the gravitational constant [6] [7] [8] [9] . The beam splitter and the mirror operations of an atom interferometer can be typically implemented in free space with a sequence of Bragg scatterings applied to a beam of cold atoms [5] [10] . Alternatively, the phase shifts can be estimated by measuring the Bloch frequency of cold atoms oscillating in vertically oriented optical lattices which have been able to evaluate the gravitational constant g with accuracy up to 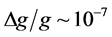 [11] [12] [13] [14] .
[11] [12] [13] [14] .
The sensitivity of light-pulse atom interferometry scales linearly with the space-time area enclosed by the interfering atoms. Large-momentum-transfer (LMT) beam splitters have been suggested [15] and experimentally investigated [16] [17] [18] , demonstrating up to 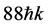 splitting (where
splitting (where 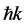 is the photon momentum) [16] [18] . Relative to the 2-photon processes used in the current most sensitive light-pulse atom interferometers, LMT beam splitters in atomic fountains can provide a 44-fold increased phase shift sensitivity [16] . Further increases of the momentum differences between the interferometer paths are limited by the cloud’s transverse momentum width since high efficiency beam splitting and mirror processes require a narrow distribution [19] .
is the photon momentum) [16] [18] . Relative to the 2-photon processes used in the current most sensitive light-pulse atom interferometers, LMT beam splitters in atomic fountains can provide a 44-fold increased phase shift sensitivity [16] . Further increases of the momentum differences between the interferometer paths are limited by the cloud’s transverse momentum width since high efficiency beam splitting and mirror processes require a narrow distribution [19] .
As an alternative to the atomic fountains, where the atoms follow ballistic trajectories, the interferometric operations can be implemented with trapped clouds [20] [21] [22] . We have recently proposed [23] a multi-mode interferometer with harmonically confined atoms where multi beam-splitter and mirror operations are realized with Kapitza-Dirac (KD) pulses, namely, the impulse application of an off-resonant standing optical wave. With KD pulses applied to atoms in a harmonic trap, it is possible to reach large spatial separations between the interferometric modes by avoiding, at the same time, atom losses and defocusing occurring in Bragg processes (mostly due to the constraint of narrow momentum widths). In [23] , the role of mirrors is played by the harmonic trap, which coherently drives and recombines a tunable number of spatially addressable atomic beams created by the KD pulses. The phase estimation sensitivity linearly increases with the number of beams and their spatial distance. The number of beams is proportional to the strength of the applied KD pulse while their distance is proportional to the ratio between the harmonic trap length and the wave-length of the optical wave. In this manuscript we discuss in detail the theory of the multi-modes KD interferometer which was introduced in [23] .
2. Multi-Modes Kaptiza-Dirac Interferometer
The initial configuration of the interferometer is provided by a cloud of cold atoms trapped by an harmonic potential . The interferometric sequence is realised in four steps, see Figure 1:
. The interferometric sequence is realised in four steps, see Figure 1:
i) Beam-splitter: A KD pulse is applied to the atomic cloud state at the time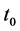 . KD creates a number of spatially addressable atomic wave-packets that evolve along different paths under the harmonic confinement.
. KD creates a number of spatially addressable atomic wave-packets that evolve along different paths under the harmonic confinement.
Figure 1. (color-online) Multimodes Kapitza-Dirac interferometer. The first Kapitza-Dirac pulse at 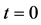 creates several modes consisting of atomic wave-packets evolving under the harmonic confinement and an external perturbing field. The n-th Kapitza-Dirac pulse at
creates several modes consisting of atomic wave-packets evolving under the harmonic confinement and an external perturbing field. The n-th Kapitza-Dirac pulse at 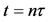 mixes the modes which are eventually detected in output at
mixes the modes which are eventually detected in output at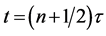 , where
, where .
.
ii) Phase shift: Each spatial mode gains a phase shift 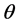 with respect to its neighbour’s modes due to the action of an external potential.
with respect to its neighbour’s modes due to the action of an external potential.
iii) Beam splitter: the harmonic trap coherently recombines the wave packets and a second KD pulse is applied to again mix and separate the modes along different paths.
iv) Measurement: The phase shift is estimated by fitting the atomic density profile or by counting the number of atoms in each spatial mode at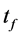 . The measurement can be done after ballistic expansion by optimising spatial separation of the modes and atom counting signal to noise ratio.
. The measurement can be done after ballistic expansion by optimising spatial separation of the modes and atom counting signal to noise ratio.
The sequences i)-iii) can be iterated an arbitrary number of times n before the final measurement iv).
The plan of the paper is as follows. In Section 2, we present a detailed description of the multi-modes KD interferometer. As an application we calculate the Fisher information and the Cramér-Rao lower bound sensitivity [24] of the interferometric measurement of the gravitational constant g in Section 3. We predict sensitivities up to 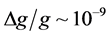 in configurations realisable within the current state of the art and in the Section 4 we compare the performance of different atomic interferometers. In Section 5 we discuss two possible sources of noise and we finally summarise the results in Section 6.
in configurations realisable within the current state of the art and in the Section 4 we compare the performance of different atomic interferometers. In Section 5 we discuss two possible sources of noise and we finally summarise the results in Section 6.
3. Dynamics
Let’s consider first a single atom described by a wave packet 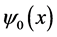 confided in the harmonic trap
confided in the harmonic trap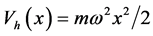 . The time evolution of the state in the harmonic trap is given by
. The time evolution of the state in the harmonic trap is given by
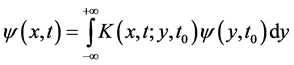 (1)
(1)
where 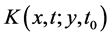 is the quantum propagator [25]
is the quantum propagator [25]
 (2)
(2)
with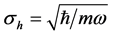
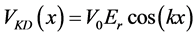
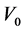
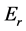
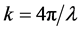
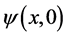
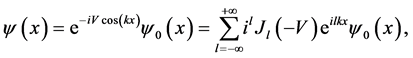
where we have used the Bessel generating function 
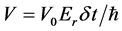

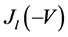
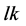
After the application of the first KD, the wave-packets are coherently driven by the harmonic trap and recombined after a time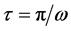
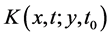
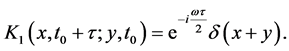
Furthermore, in presence of an external field, each spatial mode created by the KD beam splitter gains during the time 
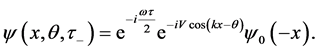
After iterating a number of times n the sequence of KD pulses and phase shift accumulations, the wave function at 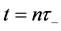
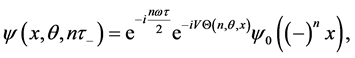
where
and 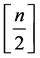
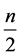
while for even n we have
After n iterations, a last KD pulse is applied at the time 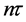
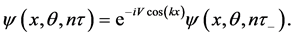
The wave packets gain their maximum spatial separation after a further 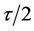
Eventually, the wave function at the final time 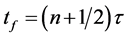
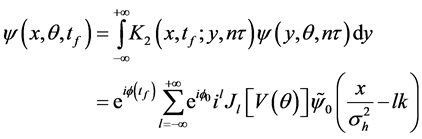
where

and
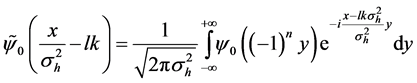
with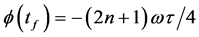
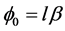
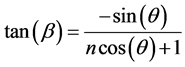
In the limit if zero overlap between the various wave packets in Equation (8),
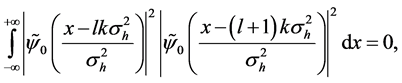
the density function at the measurement time 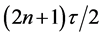
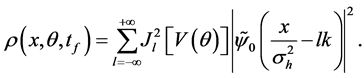
Equation (12) shows that there are 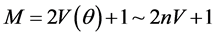
In the limit of a large number 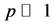
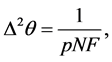
where N is the number of uncorrelated atoms. F denotes the Fisher information calculated from the particle density at the measurement time
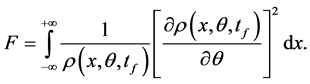
With Equation (12), Equation (14) becomes
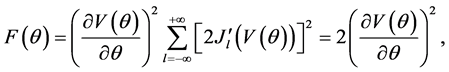
(see Appendix). We finally obtain
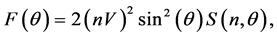
where
Notice that even in the case of a odd value of n, with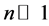
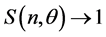
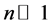
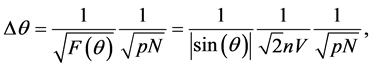
which can also be written as
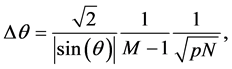
since the total number of modes is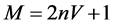
We remark here the important condition of non overlap of the wave packets corresponding to the different momentum modes at the time of measurement, Equation (11). A further interesting point is that Equation (18) is independent from the temperature of the atoms as long as their de Broglie wavelength remains larger than the internal spatial separation of the periodic potential creating the Kapitza-Dirac pulse. We will show this in the following Sections by considering as a specific application the interferometric estimation of the gravitational constant.
4. Estimation of the Gravitational Acceleration Constant g
We now investigate the KD interferometer theory to estimate the gravity constant g. The evolution of the initial state 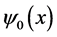
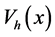
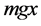
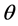
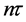

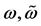
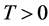
To take in account the effect of the gravitational force on the dynamical evolution of the trapped atom states, we need to include in the free propagator 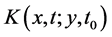
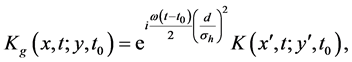
where 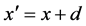

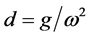
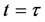
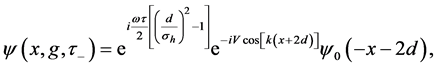
since the quantum propagator undergone with gravity field is reduced to
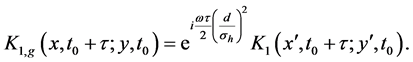
As expected, each spatial mode gains its phase shift 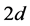
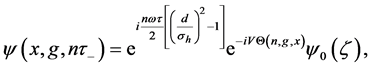
where 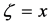
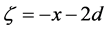
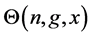
and for even n
The last KD pulse is applied on the wave function Equation (22) at time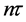

Firstly, we consider the case without the gravity field. Then at the time 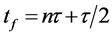
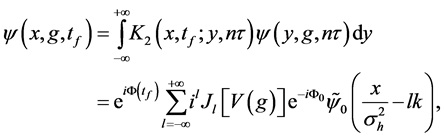
where 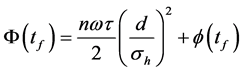
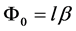
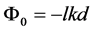
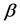
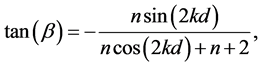
and 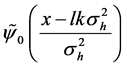

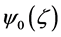
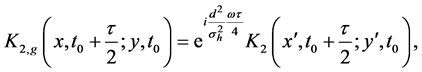
where 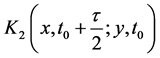
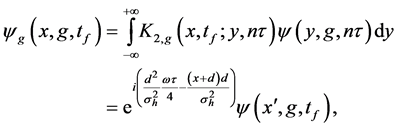
where 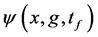
Except the phase difference between Equation (24) and Equation (27), a constant difference d is found in the centre position of each sub-wave packets induced by the gravity field. In the case of “no-overlap” condition (Equation (11)), which is satisfied when the width of the initial wave packet is much larger than the interwell distance of the KD optical lattice (
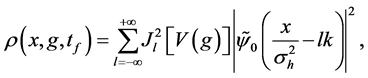
from Equation (24) or
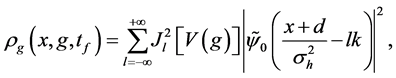
from Equations ((27), (12) and (28)) show that the information on the estimated values of 
We now consider an atomic gas at finite temperature T. To get some simple insight on the physics of the problem, we consider the system as made by a swarm of minimum uncertainty Gaussian wave packets

where the initial wave packet width 
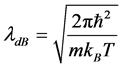
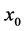
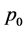
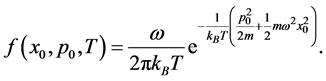
Each wav packet evolves driven by the propagators calculated in the previous Section:
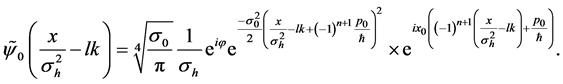
and
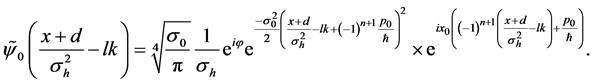
where 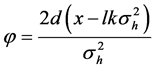

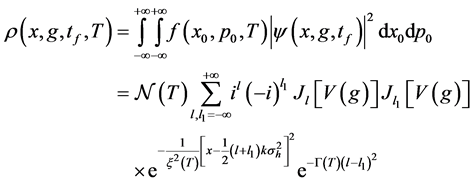
where 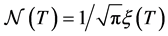
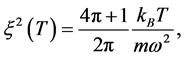
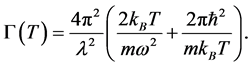
It is interesting to note that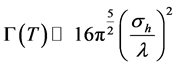
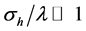
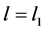
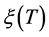
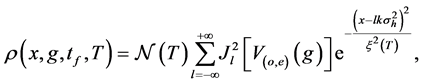
or
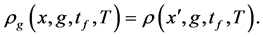
Notice that the value of the gravitational constant g is only contained in the weights of the modes.
The requirement is that sub-wave packets in Equation (37) are spatially separated, which means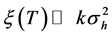
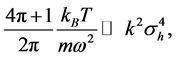
which means

As expected, the spatial separation condition in Equation (37) 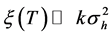
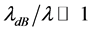
Substituting the density function Equation (37) at the measurement time 
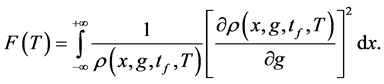
The Fisher information for our system depends on the temperature, initial density profile, the interferometer transformation, and the choice of the observable that, here, is the spatial position of atoms. In this case, the estimator can simply be a fit of the final density profile. However, the same results would be obtained by choosing as observable, the number of particles in each Gassian spatial mode. Since the initial state is made of uncorrelated atoms, there is no need to measure correlations between the modes in order to saturate the Cramér-Rao lower bound Equation (13) at the optimal value of the value phase shift.
Before proceeding to discuss the finite temperature case, we calculate the highest sensitivity of the unbiased estimation of parameter g, which is guaranteed by the no-overlap condition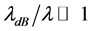
In the limit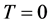
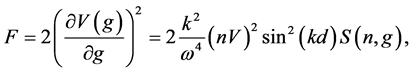
where 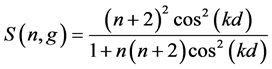
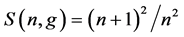
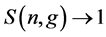
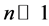
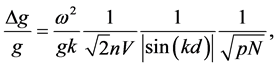
The Equation (43) can be rewritten as
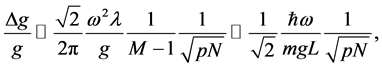
where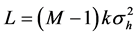
If the gravity field is witched on in the last KD pulse, the density profile at final time is described by Equation (38). In this case, there is a further contribution to the Fisher Equation (42) from the shift on the center of sub-wave packets and we have
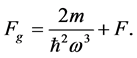
5. Sensitivity
We now estimate the expected sensitivity under realistic experiment conditions. We consider 105 88Sr atoms trapped in an harmonic trap having 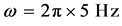
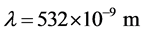
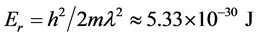
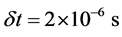
With a strength of the KD potential 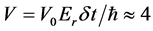
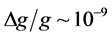
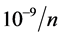
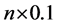
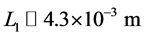
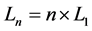
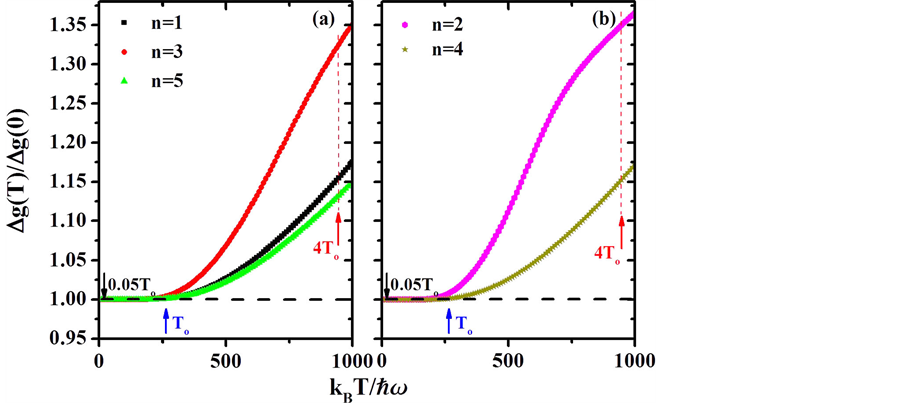
Since the thermal de Broglie wavelength decreases when increasing the temperature, the no-overlap condition Equation (11) breaks down at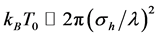
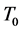
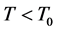
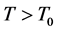
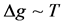
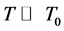
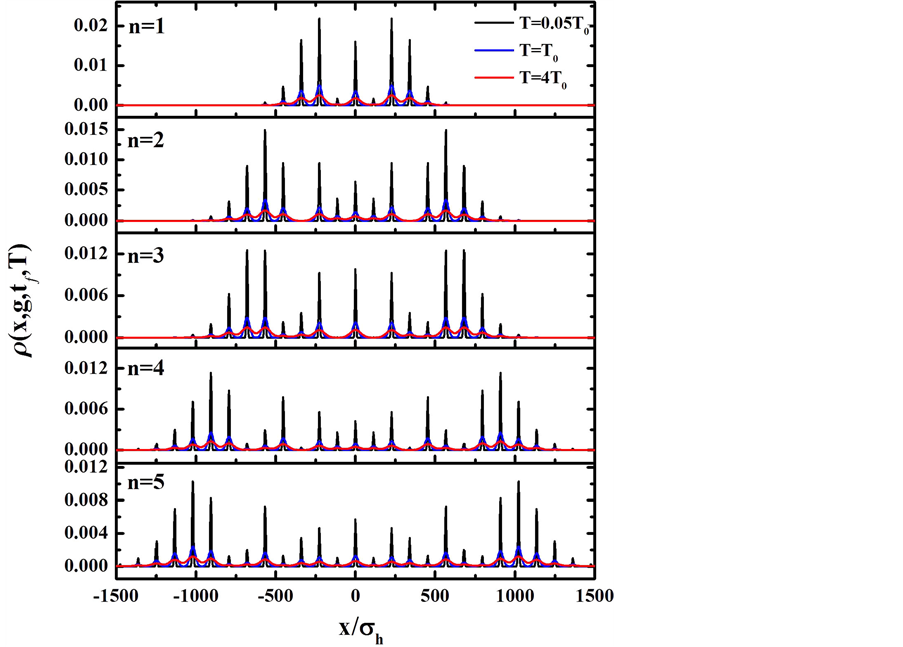
Figure 2. (color-online) Normalized phase estimation sensitivity as a function of the temperature for even and odd n.
Figure 3. (color-online) Density profiles of the output wave function of Figure 2. The dark line, blue line and red line show temperatures below, equal and above the crossover temperature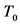
As a comparison with current atom interferometers, we calculate the sensitivity obtained from a simple interference pattern observed after a free expansion of an initial atom clouds relevant, for instance, when measuring the gravitational constant g using Bloch oscillations [12] [13] [14] . As shown in [32] , the momentum distribution is expressed as
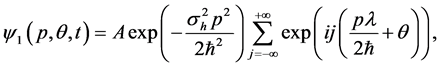
where 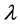
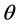
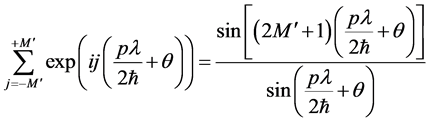
where 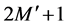
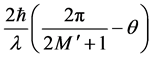
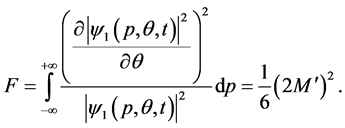
where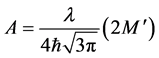
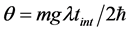
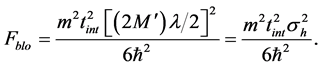
where 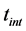
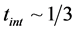
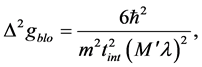
where we have estimated the maximum occupied lattice sites by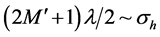
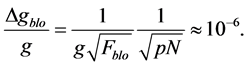
Considering the sensitivity for a single Kaptiza-Dirac pulse with Equation (51), we can reach a sensitivity larger than 3 order of magnitude that the sensitivity obtained in an interference pattern. The reason is that the KD pulses can create several wave packets spanning a distance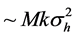
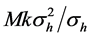
6. Noise and Decoherence
We now consider the effects of noise and imperfections on the sensitivity of the interferometer. We mainly consider two kinds of perturbations, which may arise from the experimental realization of the interferometry. The first one is the effect of the anharmonicity, described by a position dependent random perturbation, and the second one the effect of a shift in position between different sequences of the KD pulses.
The effect of anharmonicity is investigated by numerically simulating the interferometric sequences with the following potential
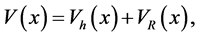
where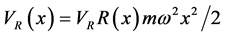
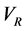

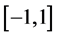
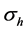
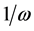
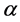

Starting with the ground state of the harmonic trap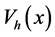
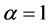
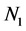
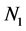
the average density 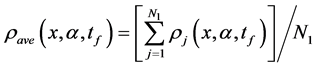
information 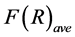
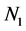
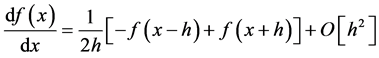
Due to the perturbation potential
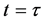
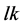
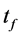
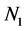
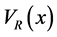
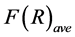
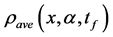
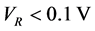
A shift of the optical lattice with respect to the harmonic trap 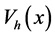
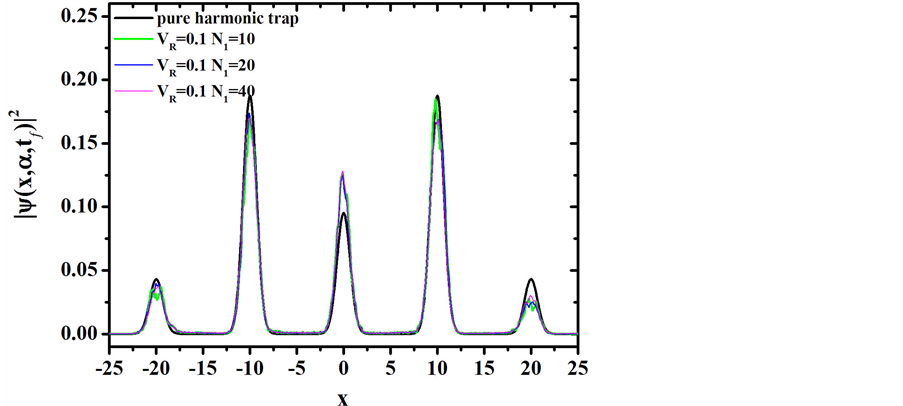
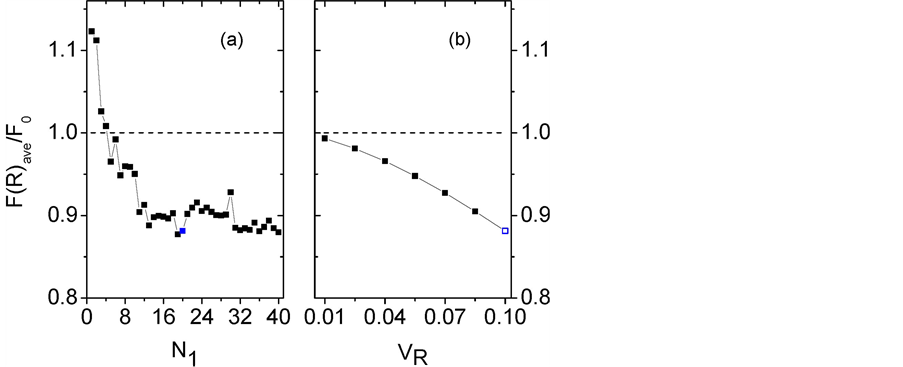
Figure 4. (color-online) Density profiles around each momentum component 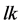
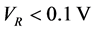
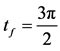
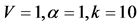
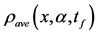
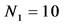


Figure 5. (color-online) The average Fisher information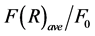
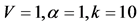
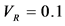

tive KD pulses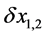
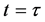
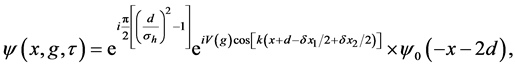
where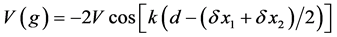
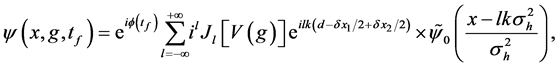
where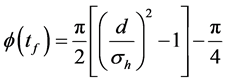
makes only an phase shifts for each sub-wave packets. Therefore, the non-overlap condition Equation (11) does not have any modification even after considering the off-center shift In this case, the final density profiles is

Equation (56) shows that the center shifts could induce a fluctuation by 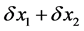
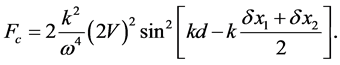
7. Conclusion
During the last few decades, matter-wave interferometry has been successfully extended to the domain of atoms and molecules. Most current interferometric protocols for the measurement of gravity or inertial forces are based on the manipulation of free falling atoms realizing Mach-Zehnder like configurations. Here we propose an atomic multimode interferometer with atoms trapped in a harmonic potential and where the multi beam-splitter operation are implemented with Kapitza-Dirac pulses. The mirror operations are performed by the harmonic trap which coherently drives a tunable number of spatially addressable atomic beams. All interferometer processes, including splitting, phase accumulation and reflection are performed and completed within the harmonic trap. Therefore, all trapped atoms contribute to the sensitivity. We have applied our scheme to the estimation of the gravitational constant and estimate, with realistic experimental parameters, a sensitivity of 10−9, significantly exceeding the sensitivity of current interferometric protocols.
Acknowledgements
Our work is supported by the National Science Foundation of China (No. 11374197), PCSIRT (No. IRT13076), the National Science Foundation of China (No.11504215).
Cite this paper
Cheng, R.L., He, T.C., Li, W.D. and Smerzi, A. (2016) Theory of a Kaptiza-Dirac Interferometer with Cold Trapped Atoms. Journal of Modern Physics, 7, 2043-2062. http://dx.doi.org/10.4236/jmp.2016.715180
References
- 1. Abbott, B.P., et al. (2016) Physical Review Letters, 116, Article ID: 241103.
http://dx.doi.org/10.1103/PhysRevLett.116.241103 - 2. Zehnder, L. (1891) Zt. Instrumentenkd, 11, 275.
- 3. Culshaw, B. (2006) Measurement Science and Technology, 17, R1.
http://dx.doi.org/10.1088/0957-0233/17/1/R01 - 4. Cronin, A.D., Schmiedmayer, J. and Pritchard, D.E. (2009) Reviews of Modern Physics, 81, 1051.
http://dx.doi.org/10.1103/RevModPhys.81.1051 - 5. Fixler, J.B., Foster, G.T., McGuirk, J.M. and Kasevich, M.A. (2007) Science, 315, 74-77.
http://dx.doi.org/10.1126/science.1135459 - 6. Rosi, G., Sorrentino, F., Cacciapuoti, L., Prevedelli, M. and Tino, G.M. (2014) Nature (London), 510, 518-521.
http://dx.doi.org/10.1038/nature13433 - 7. Biedermann, G.W., Wu, X., Deslauriers, L., Roy, S., Mahadeswaraswamy, C. and Kasevich, M.A. (2015) Physical Review A, 91, Article ID: 033629.
http://dx.doi.org/10.1103/PhysRevA.91.033629 - 8. Zhou, L., Long, S.T., Tang, B., Chen, X., Gao, F., Peng, W.C., Duan, W.T., Zhong, J.Q., Xiong, Z.Y., Wang, J., Zhang, Y.Z. and Zhan, M.S. (2015) Physical Review Letters, 115, Article ID: 013004.
http://dx.doi.org/10.1103/PhysRevLett.115.013004 - 9. Chaibi, W., Geiger, R., Canuel, B., Bertoldi, A., Landragin, A. and Bouyer, P. (2016) Physical Review D, 93, Article ID: 021101(R).
http://dx.doi.org/10.1103/PhysRevD.93.021101 - 10. Keller, C., Schmiedmayer, J., Zeilinger, A., Nonn, T., Dürr, S. and Rempe, G. (1999) Applied Physics B, 69, 303-309.
http://dx.doi.org/10.1007/s003400050810 - 11. Roati, G., de Mirandes, E., Ferlaino, F., Ott, H., Modugno, G. and Inguscio, M. (2004) Physical Review Letters, 92, Article ID: 230402.
http://dx.doi.org/10.1103/PhysRevLett.92.230402 - 12. Ferrari, G., Poli, N., Sorrentino, F. and Tino, G.M. (2006) Physical Review Letters, 97, Article ID: 060402. http://dx.doi.org/10.1103/PhysRevLett.97.060402
- 13. Poli, N., Wang, F.-Y., Tarallo, M.G., Alberti, A., Prevedelli, M. and Tino, G.M. (2011) Physical Review Letters, 106, Article ID: 038501.
http://dx.doi.org/10.1103/PhysRevLett.106.038501 - 14. Tarallo, M.G., Alberti, A., Poli, N., Chiofalo, M.L., Wang, F.-Y. and Tino, G.M. (2012) Physical Review A, 86, Article ID: 033615.
http://dx.doi.org/10.1103/PhysRevA.86.033615 - 15. Denschlag, J.H., et al. (2002) Journal of Physics B: Atomic, Molecular and Optical Physics, 35, 3095.
http://dx.doi.org/10.1088/0953-4075/35/14/307 - 16. Müller, H., Chiow, S.-W., Long, Q., Herrmann, S. and Chu, S. (2008) Physical Review Letters, 100, Article ID: 180405.
http://dx.doi.org/10.1103/PhysRevLett.100.180405 - 17. Cladé, P., Guellati-Khélifa, S., Nez, F. and Biraben, F. (2009) Physical Review Letters, 102, Article ID: 240402.
http://dx.doi.org/10.1103/PhysRevLett.102.240402 - 18. Müller, H., Chiow, S.-W., Herrmann, S. and Chu, S. (2009) Physical Review Letters, 102, Article ID: 240403.
http://dx.doi.org/10.1103/PhysRevLett.102.240403 - 19. Szigeti, S.S., Debs, J.E., Hope, J.J., Robins, N.P. and Close, J.D. (2012) New Journal of Physics, 14, Article ID: 023009.
http://dx.doi.org/10.1088/1367-2630/14/2/023009 - 20. Garcia, O., Deissler, B., Hughes, K.J., Reeves, J.M. and Sackett, C.A. (2006) Physical Review A, 74, Article ID: 031601(R).
http://dx.doi.org/10.1103/PhysRevA.74.031601 - 21. Sapiro, R.E., Zhang, R. and Raithel, G. (2009) Physical Review A, 79, Article ID: 043630.
http://dx.doi.org/10.1103/PhysRevA.79.043630 - 22. Close, J. and Robins, N. (2012) Physics, 5, 26.
http://dx.doi.org/10.1103/Physics.5.26 - 23. Li, W.D., He, T.C. and Smerzi, A. (2014) Physical Review Letters, 113, Article ID: 023003.
http://dx.doi.org/10.1103/PhysRevLett.113.023003 - 24. Pezzé, L. and Smerzi, A. (2014) Atom Interferometry. Proceedings of the International School of Physics “Enrico Fermi”, Course 188, Societa’ Italiana di Fisica, Bologna and IOS Press, Amsterdam.
- 25. Holstein, B.R. (1992) Topics in Advanced Quantum Mechanics. Addison-Wesley, Reading, MA.
- 26. Edwards, M., Benton, B., Heward, J. and Clark, C.W. (2010) Physical Review A, 82, Article ID: 063613.
http://dx.doi.org/10.1103/PhysRevA.82.063613 - 27. Moharam, M.G. and Young, L. (1978) Applied Optics, 17, 1757-1759.
http://dx.doi.org/10.1364/AO.17.001757 - 28. Abramowitz, M. and Stegun, I.A. (1970) Handbook of Mathematical Functions: With Formulas, Graphs and Mathematical Tables. National Bureau of Standards, Washington DC.
- 29. Deng, L., Hagley, E., Denschlag, J., Simsarian, J., Edwards, M., Clark, C., Helmerson, K., Rolston, S. and Phillips, W. (1999) Physical Review Letters, 83, 5407.
http://dx.doi.org/10.1103/PhysRevLett.83.5407 - 30. Hyllus, P., Laskowski, W., Krischek, R., Schwemmer, C., Wieczorek, W., Weinfurter, H., Pezze, L. and Smerzi, A. (2012) Physical Review A, 85, Article ID: 022321.
http://dx.doi.org/10.1103/PhysRevA.85.022321 - 31. Chwedenczuk, J., Piazza, F. and Smerzi, A. (2013) Physical Review A, 87, Article ID: 033607.
http://dx.doi.org/10.1103/PhysRevA.87.033607 - 32. Pedri, P., Pitaevskii, L., Stringari, S., et al. (2001) Physical Review Letters, 87, Article ID: 220401.
http://dx.doi.org/10.1103/PhysRevLett.87.220401 - 33. Bandrauk, A.D. and Shen, H. (1994) Journal of Physics A: Mathematical and General, 27, 7147.
http://dx.doi.org/10.1088/0305-4470/27/21/030
Appendix
Appendix A
To obtain Equation (15), we have considered the Bessel functions identity
With this we have
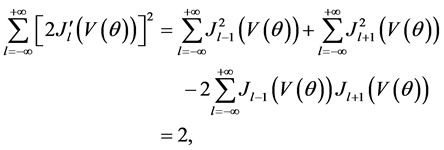
where one more identity
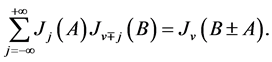
has been used to obtain
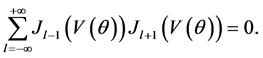
Appendix B
For Equation (45), Using the Equation (41) and Equation (29), we obtain
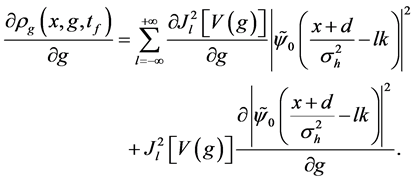
By using the initial state
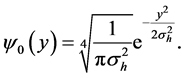
we get
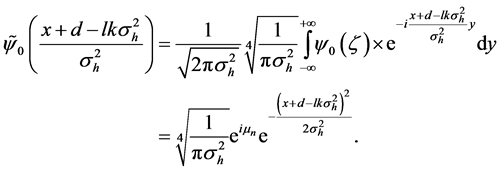
where 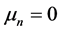
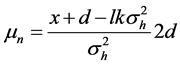
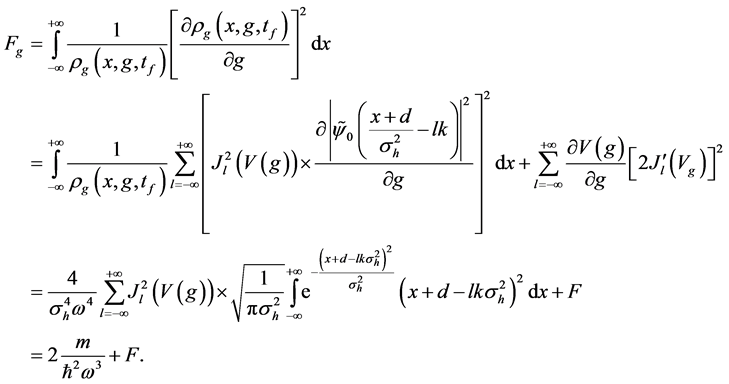
The second step uses the “no-overlap” condition by changing 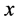
Submit or recommend next manuscript to SCIRP and we will provide best service for you:
Accepting pre-submission inquiries through Email, Facebook, LinkedIn, Twitter, etc.
A wide selection of journals (inclusive of 9 subjects, more than 200 journals)
Providing 24-hour high-quality service
User-friendly online submission system
Fair and swift peer-review system
Efficient typesetting and proofreading procedure
Display of the result of downloads and visits, as well as the number of cited articles
Maximum dissemination of your research work
Submit your manuscript at: http://papersubmission.scirp.org/
Or contact jmp@scirp.org