Journal of Modern Physics
Vol.07 No.13(2016), Article ID:70649,34 pages
10.4236/jmp.2016.713152
Black Body Quantum Fluctuations and Relativity
Sebastiano Tosto
Retired Physicist, ENEA Casaccia, Roma, Italy

Copyright © 2016 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: July 20, 2016; Accepted: September 16, 2016; Published: September 19, 2016
ABSTRACT
The paper introduces a simple theoretical model aimed to provide a possible derivation of the quantum fluctuations of the black body radiation. The model offers the chance of inferring and linking contextually quantum and relativistic results.
Keywords:
Quantum Physics, Thermodynamics, Relativity

1. Introduction
In 1859, Kirchhoff had the remarkable idea that a small hole in the side of a massive body of material containing a large cavity was the best experimental approximation of the concept of total absorber: the radiation penetrating through the hole was correctly assumed bouncing between the internal walls of the cavity with a little probability of escaping outside. With this viewpoint, still today acknowledged [1] , Planck modeled 1901 the thermodynamic equilibrium of the radiation field inside the cavity. Since any thermodynamic system is subjected to statistical fluctuations around the equilibrium configuration, Einstein proposed in 1909 a theoretical model about these fluctuations working on the Planck result. The Einstein model was focused essentially on the black body radiation assumed at the equilibrium in a cavity with perfectly reflecting walls. This assumption arose however the difficulty of explaining the thermalization mechanism of the radiation field. The second law of thermodynamics states that any system left undisturbed for a sufficiently long time tends to the equilibrium state [2] ; nevertheless the thermalization time of photons at temperatures below 109 K is expectedly very long, as their direct interaction is negligible compared to that with matter [3] . The fact that the thermalization process is slightly shortened in the presence of rarefied gas particles [4] , shows that in fact the interaction of photons with matter, i.e. with the internal walls of the cavity, is required to explain the equilibrium condition of the black body at the usual temperatures and times at which is tested the Planck law. The equilibrium condition is attained therefore considering partially reflecting walls of the cavity to promote the photon-solid matter interaction mechanism via continuous absorption and reemission of radiation.
The problem of the quantum fluctuations of black body radiation is still today debated for its theoretical interest [5] [6] , in particular as concerns the thermalization mechanism of the photons in the cavity. Just this is the problem: any model aimed to describe the Planck law and its transient deviations from the equilibrium should infer explicitly this kind of interaction, without need of postulating it separately and purposely. Moreover, the fluctuation of a thermodynamic system implies in general several non-equilibrium phenomena, e.g. local temperature gradients and configuration changes; specifically, are expected gradients of radiation frequency and mass evaporated from the internal surface of the cavity, whose dynamics contributes to the thermalization of photons.
While focusing on the radiation field only seems reductive, the variety of phenomena involved when a black body system is out of the equilibrium suggests the usefulness of a comprehensive approach to the problem and introduces the three main motivations of this paper:
1) To propose a model where the photon interaction with the walls of the cavity appears as a natural consequence of the theoretical approach underlying the black body physics.
2) To highlight the thermodynamic aspects of the black body fluctuations with reference to their quantum basis, in particular the uncertainty principle.
3) To show that relativistic results are also obtainable in the frame of a unique conceptual model.
After a preliminary outline of the main dynamical variables prospectively implicated in the problem, the model is specifically addressed to introduce not only the fluctuation but also the main physical laws expectedly useful to describe it. Despite the inherent complexity of the problem, the exposition is organized in order to be as simple, gradual and self-contained as possible.
2. Preliminary Considerations
Consider one free particle of mass m moving within a space range 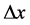 during a time range
during a time range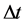 . It is in principle possible to express
. It is in principle possible to express 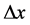 as a function of the Compton length
as a function of the Compton length 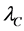 of the particle; so define the range size in
of the particle; so define the range size in 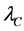 units putting
units putting
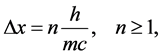 (1)
(1)
where n is an arbitrary real number. The second position emphasizes that the range 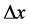 where the particle is allowed to move cannot be smaller than
where the particle is allowed to move cannot be smaller than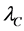 , which is an intrinsic physical property of the particle itself through its mass m.
, which is an intrinsic physical property of the particle itself through its mass m.
In principle, nothing hinders to express the numerical parameter n as the ratio , being v the component of velocity of the particle along
, being v the component of velocity of the particle along : is attracting the chance that
: is attracting the chance that 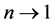 is consistent with
is consistent with 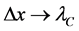 whereas
whereas 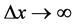 for
for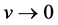 , in agreement with the arbitrary size of
, in agreement with the arbitrary size of 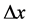 and value of v in a given reference system R. The formal choice of introducing the range size in
and value of v in a given reference system R. The formal choice of introducing the range size in 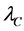 units does not exclude thinking even a photon confined in
units does not exclude thinking even a photon confined in 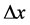 during a time range
during a time range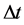 , which compels therefore defining
, which compels therefore defining![]() . Dividing both sides of Equation (1) by
. Dividing both sides of Equation (1) by![]() , one finds in R
, one finds in R
![]()
Defining the link between time and space range sizes via c, in order to ensure that any massive particle is effectively confined within ![]() during
during![]() , the positions
, the positions
![]() (2)
(2)
yield
![]() (3)
(3)
The first equation simply rewrites ![]() as
as![]() , being
, being![]() .
.
Simple considerations show that these positions are physically sensible. The first equation reads indeed
![]() (4)
(4)
i.e. ![]() is related to the wavelength
is related to the wavelength![]() . Regard
. Regard ![]() with the physical meaning of wavelength of matter wave introducing a multiplicative factor
with the physical meaning of wavelength of matter wave introducing a multiplicative factor ![]() necessary to express the wavelength as a function of v instead of c, as it appears in the third equation. Divide both sides of the first equation by the arbitrary number
necessary to express the wavelength as a function of v instead of c, as it appears in the third equation. Divide both sides of the first equation by the arbitrary number![]() ; one obtains
; one obtains
![]() (5)
(5)
so that ![]() is in effect defined by
is in effect defined by ![]() instead of c; then
instead of c; then
![]()
yields
![]() (6)
(6)
In other words, the matter wave propagating at rate ![]() implies
implies ![]() in agreement with
in agreement with![]() . The result (6) is interesting because it is easy to show that
. The result (6) is interesting because it is easy to show that
![]() (7)
(7)
so, through the position![]() , Equation (6) yield the De Broglie wave momentum of the particle and contextually the relativistic expressions of energy and momentum, whereas Equations (1) and (6) imply the corpuscle/wave dual behavior of matter.
, Equation (6) yield the De Broglie wave momentum of the particle and contextually the relativistic expressions of energy and momentum, whereas Equations (1) and (6) imply the corpuscle/wave dual behavior of matter.
To check this point, replace in the first Equation (6)![]() , so that
, so that ![]() and thus
and thus![]() ; hence
; hence
![]()
At the left hand side appears the Lagrangian L of the free particle, which correctly results as a difference of two energies. Indeed by definition![]() , so that
, so that![]() . The concept of action
. The concept of action ![]() also follows by consequence. Note that in the expressions (6) of
also follows by consequence. Note that in the expressions (6) of ![]() and p appears the ratio
and p appears the ratio![]() ; admitting that this ratio is finite even in the limit
; admitting that this ratio is finite even in the limit ![]() if contextually
if contextually![]() , thus obtaining the undetermined form 0/0, one finds
, thus obtaining the undetermined form 0/0, one finds ![]() and
and ![]() having put by definition
having put by definition
![]() (8)
(8)
This limit holds for a photon wave, in which case Equation (6) yields![]() . For a massive particle instead
. For a massive particle instead
![]() (9)
(9)
If ![]() is an invariant expression of momentum, then the right hand side must be an invariant quantity as well; in effect
is an invariant expression of momentum, then the right hand side must be an invariant quantity as well; in effect ![]() for
for ![]() is the Lorentz transformation of
is the Lorentz transformation of ![]() between inertial reference systems displacing at rate v, in either of which the particle is at rest. Moreover it appears that
between inertial reference systems displacing at rate v, in either of which the particle is at rest. Moreover it appears that ![]() is not mere numerical factor, actually it allows linking the cases
is not mere numerical factor, actually it allows linking the cases ![]() and
and ![]() depending on whether
depending on whether![]() .
.
These conclusions are inferred regarding in particular ![]() as a mere range size; i.e. the kinetic properties of a free particle follow simply as a consequence of the space and time ranges available to and compatible with its dynamical behavior. The frequency
as a mere range size; i.e. the kinetic properties of a free particle follow simply as a consequence of the space and time ranges available to and compatible with its dynamical behavior. The frequency ![]() defines the range size
defines the range size
![]() (10)
(10)
according to Equation (2); i.e., in agreement with the dual behavior of matter, the range size is related via ![]() to the wavelength of the pertinent matter wave.
to the wavelength of the pertinent matter wave.
Furthermore, an interesting consequence follows regarding ![]() as a physical constrain to the particle delocalization: for example one could suppose that
as a physical constrain to the particle delocalization: for example one could suppose that ![]() is delimited by two infinite potential walls that define its boundaries, in which case the particle must be thought bouncing back and forth in a given space range without chance of escaping. In other words, Equation (1) does not exclude that t the time
is delimited by two infinite potential walls that define its boundaries, in which case the particle must be thought bouncing back and forth in a given space range without chance of escaping. In other words, Equation (1) does not exclude that t the time ![]() the particle could be located at
the particle could be located at![]() , as instead it is purposely excluded now. If so, then
, as instead it is purposely excluded now. If so, then ![]() is actually an one-dimensional cavity; thus the concept of frequency
is actually an one-dimensional cavity; thus the concept of frequency ![]() is no longer the reciprocal time range
is no longer the reciprocal time range ![]() necessary for the photon to travel
necessary for the photon to travel![]() , rather it is related to the bouncing rate physically implied by the boundary potential walls. This is understandable thinking a steady photon wave with wavelength
, rather it is related to the bouncing rate physically implied by the boundary potential walls. This is understandable thinking a steady photon wave with wavelength ![]() or matter wave with wavelength
or matter wave with wavelength ![]() of Equation (5), both additional to all wavelengths allowed in the cavity. So, owing to Equation (2), the lowest frequencies allowed for photon or massive particle traveling through
of Equation (5), both additional to all wavelengths allowed in the cavity. So, owing to Equation (2), the lowest frequencies allowed for photon or massive particle traveling through ![]() are respectively with obvious notation
are respectively with obvious notation
![]() (11)
(11)
Consequently the minimum energies ![]() and
and ![]() regard
regard ![]() as a one- dimensional cavity where matter particles or even photons are confined without chance of escaping. Note that
as a one- dimensional cavity where matter particles or even photons are confined without chance of escaping. Note that ![]() and
and ![]() have been inferred in Equation (11) after having simulated a confinement mechanism constraining any particle to move within
have been inferred in Equation (11) after having simulated a confinement mechanism constraining any particle to move within![]() ; it is easy to show however the possibility of reversing this path, i.e. that once admitting the existence of the limit momentum wavelengths
; it is easy to show however the possibility of reversing this path, i.e. that once admitting the existence of the limit momentum wavelengths ![]() and
and ![]() it is possible to infer a mechanism that constrains the motion of any particle within
it is possible to infer a mechanism that constrains the motion of any particle within ![]() only. This point is highlighted just below and later in the Section 7.
only. This point is highlighted just below and later in the Section 7.
Implement to this purpose the case of a particle bouncing elastically back and forth against either boundary wall that delimits the confinement range, Equation (11); the momentum change of the particle reads thus![]() . If the bouncing lasts a time range
. If the bouncing lasts a time range![]() , the force acting on the wall is
, the force acting on the wall is
![]()
the subscript ![]() stands for “potential wall” to stress that this particular range is able to confine any particle. It is clearly possible to express F in Planck units via an appropriate multiplicative factor q; then the last result reads
stands for “potential wall” to stress that this particular range is able to confine any particle. It is clearly possible to express F in Planck units via an appropriate multiplicative factor q; then the last result reads
![]()
which yields
![]()
This is not a hypothesis “ad hoc”, as the Planck units have fundamental worth, being based on dimensional relationships involving fundamental constants of nature. It is immediate to describe in this respect the particular case of photon confinement taking the limit for ![]() and
and![]() , which yields
, which yields ![]() according to Equation (8). Putting then
according to Equation (8). Putting then ![]() this limit corresponds to the confinement of a photon in
this limit corresponds to the confinement of a photon in ![]() and reads
and reads
![]() (12)
(12)
which expresses the condition even for a photon to be trapped inside any ![]() of such size together with M by consequence of the gravitational effect of this latter. For obvious reasons, the subscript
of such size together with M by consequence of the gravitational effect of this latter. For obvious reasons, the subscript ![]() has been replaced by that stressing the idea of M driven confinement.
has been replaced by that stressing the idea of M driven confinement.
Start eventually from the identity (1) ![]() to obtain
to obtain ![]() thanks to Equations (1) and (3); being by definition
thanks to Equations (1) and (3); being by definition![]() , one infers
, one infers ![]() whatever
whatever ![]() might be in the reference system R. Moreover, replacing p via the first Equation (6) as well, one also finds
might be in the reference system R. Moreover, replacing p via the first Equation (6) as well, one also finds![]() ; thus
; thus ![]() yields
yields ![]() in the same R. As of course
in the same R. As of course![]() , reasoning exactly as before one finds
, reasoning exactly as before one finds![]() .
.
Consider now the identity![]() , being
, being ![]() a constant momentum component, and note that the right hand side defines an arbitrary range
a constant momentum component, and note that the right hand side defines an arbitrary range ![]() whose upper and lower boundaries are
whose upper and lower boundaries are ![]() and
and ![]() respectively. Is essential the fact that both p and
respectively. Is essential the fact that both p and ![]() are arbitrary and independent each other, so that the same holds for the range size and its boundary coordinates. Regarding in an analogous way even
are arbitrary and independent each other, so that the same holds for the range size and its boundary coordinates. Regarding in an analogous way even![]() , the straightforward conclusion is
, the straightforward conclusion is
![]()
Apart from the simplicity of reasoning, is remarkable the fact that the most typical feature of the quantum physics, the Heisenberg inequalities, has been obtained from the relativistic Equation (6).
Equation (3) and other results of this section have been inferred directly from general considerations about the properties of the space time [7] in the frame of a unique and comprehensive approach “ab initio”. Equation (7) will be examined further on in the Sections 4 and 7 to clarify how these considerations are linked to the quantum fluctuations.
3. Fluctuations
This section introduces the fluctuation of all variables previously introduced, with the aim of finding possible links between these variations. Differentiate ![]() to simulate the physical idea that both energies are subjected to fluctuate: as by definition the dynamical variable of
to simulate the physical idea that both energies are subjected to fluctuate: as by definition the dynamical variable of ![]() is the mass m whereas that of E is the frequency
is the mass m whereas that of E is the frequency![]() , write thus according to Equation (3)
, write thus according to Equation (3)
![]() (13)
(13)
being
![]() (14)
(14)
These positions relate in general ![]() and
and ![]() to
to![]() . Thinking specifically the black body cavity, for example, the first Equation (14) describes the fluctuations of the amount of mass evaporated from the internal walls of the cavity, the second Equation (14) concerns the corresponding frequency fluctuation of the radiation field in it contained. Equation (13) relates them and requires temperature fluctuation too, although not yet explicitly concerned. To clarify this point note that the changes
. Thinking specifically the black body cavity, for example, the first Equation (14) describes the fluctuations of the amount of mass evaporated from the internal walls of the cavity, the second Equation (14) concerns the corresponding frequency fluctuation of the radiation field in it contained. Equation (13) relates them and requires temperature fluctuation too, although not yet explicitly concerned. To clarify this point note that the changes ![]() and
and ![]() are defined around the respective
are defined around the respective ![]() and E, which can be regarded as equilibrium values. For the following purposes it is useful to calculate the average fluctuations
and E, which can be regarded as equilibrium values. For the following purposes it is useful to calculate the average fluctuations ![]() and
and ![]() considering arbitrary fluctuation ranges around an arbitrary reference energy value. For instance
considering arbitrary fluctuation ranges around an arbitrary reference energy value. For instance ![]() is calculated considering various ranges
is calculated considering various ranges ![]() of values around the equilibrium value
of values around the equilibrium value ![]() and taking their mean value; if
and taking their mean value; if![]() , then
, then ![]() is the average fluctuation of the system matter+radiation; the same holds indeed to define
is the average fluctuation of the system matter+radiation; the same holds indeed to define![]() . In principle therefore
. In principle therefore ![]() and
and ![]() are independent of the respective
are independent of the respective ![]() and
and![]() , which will be denoted in the following as E and
, which will be denoted in the following as E and ![]() for simplicity of notation. Trivial manipulations of Equation (13) yield
for simplicity of notation. Trivial manipulations of Equation (13) yield
![]() (15)
(15)
where
![]() (16)
(16)
In general
![]() (17)
(17)
emphasizes that the variables of the problem are four and that only Y depends upon![]() . Regard first Y and
. Regard first Y and ![]() separately and introduce the mean value
separately and introduce the mean value ![]() calculated in arbitrary ranges of all variables except
calculated in arbitrary ranges of all variables except![]() . Thus
. Thus
![]()
defines
![]() (18)
(18)
of course ![]() denotes an arbitrary range of velocity components with respect to which is integrated
denotes an arbitrary range of velocity components with respect to which is integrated![]() , whereas
, whereas ![]() is the velocity fluctuation concurring together with
is the velocity fluctuation concurring together with ![]() and
and ![]() to define the relationship (13) between
to define the relationship (13) between ![]() and
and![]() . The notation emphasizes that k is actually an arbitrary numerical parameter, i.e. a scale factor dependent on
. The notation emphasizes that k is actually an arbitrary numerical parameter, i.e. a scale factor dependent on ![]() only, such that for example
only, such that for example
![]()
by consequence k is also a conversion factor such that ![]() and
and ![]() can be related to energies with different physical meaning with respect to the initial E and
can be related to energies with different physical meaning with respect to the initial E and![]() .
.
Among the possible values of Y, calculate Equation (15) with the specific value![]() ; hence, owing to Equations (3) and (13),
; hence, owing to Equations (3) and (13),
![]() (19)
(19)
This result yields:
![]() (20)
(20)
These equations are obtained simply averaging the ratios of Equation (19). It worth emphasizing that ![]() is linked to the average temperature in the case of an ideal gas where by definition the particles are non-interacting; this shows that v is the velocity of matter particles evaporated from the walls of the cavity. So
is linked to the average temperature in the case of an ideal gas where by definition the particles are non-interacting; this shows that v is the velocity of matter particles evaporated from the walls of the cavity. So ![]() is related to the equilibrium temperature of the cavity containing the black body radiation field. In this one-dimensional approach
is related to the equilibrium temperature of the cavity containing the black body radiation field. In this one-dimensional approach ![]() is the distance between two matter boundary surfaces confining m and the photon wave of frequency
is the distance between two matter boundary surfaces confining m and the photon wave of frequency![]() , both subjected to the respective fluctuations
, both subjected to the respective fluctuations ![]() and
and![]() . Also,
. Also, ![]() is the obvious consequence of the expected temperature fluctuation around the average value pertinent to
is the obvious consequence of the expected temperature fluctuation around the average value pertinent to![]() .
.
So far the first Equation (3) is the only equation correlating E and![]() . To find a second equation, the one linking E and v, consider now Equation (13) that involves the variables appearing in (17) and yields
. To find a second equation, the one linking E and v, consider now Equation (13) that involves the variables appearing in (17) and yields
![]() (21)
(21)
It is evident that a hypothesis has been introduced regarding ![]() of Equation (15) as the function
of Equation (15) as the function![]() . In principle Equation (21) is not new with respect to Equation (15); however the form of this latter was useful to infer Equation (18) and the temperature implied by Equation (20), whereas Equation (21) is now implemented thanks to its analytical form easily integrable. The solution
. In principle Equation (21) is not new with respect to Equation (15); however the form of this latter was useful to infer Equation (18) and the temperature implied by Equation (20), whereas Equation (21) is now implemented thanks to its analytical form easily integrable. The solution
![]() (22)
(22)
is the sought second equation linking E and v; the notation emphasizes that the integration constant ![]() has physical dimensions of momentum. Put
has physical dimensions of momentum. Put
![]() (23)
(23)
which yields at the first order of approximation
![]() (24)
(24)
if the position (23) is correct, then even this lowest order of approximation should give a sensible result. The validity of Equation (24) is preliminarily proven recalling Equations (3), according which v yields
![]()
and then
![]()
so, neglecting preliminarily the third addend at the right hand side, this result reads![]() , having put
, having put ![]() and
and![]() . With the integration constant
. With the integration constant![]() , therefore, the result is nothing else but the statement
, therefore, the result is nothing else but the statement ![]() of Equation (1). Clearly with an appropriate choice of the integration constant this inequality holds even retaining the
of Equation (1). Clearly with an appropriate choice of the integration constant this inequality holds even retaining the ![]() term.
term.
Before proceeding, it is useful to verify further the validity of the equations hitherto inferred, in particular as concerns the physical meaning of the series expansion (23) of Equation (15). A simple one-dimensional approach is still enough for the present purposes.
4. Check of the Preliminary Results
Recalling Equations (10) and (1), trivial manipulations show that Equation (19) reads
![]() (25)
(25)
The first equation links ![]() and
and![]() : if in particular
: if in particular ![]() is due to the change of photon frequency in
is due to the change of photon frequency in![]() , then it can be nothing else but the quantum fluctuation of the radiation field in the range; also,
, then it can be nothing else but the quantum fluctuation of the radiation field in the range; also, ![]() is related to the mass fluctuation rate
is related to the mass fluctuation rate ![]() occurring at a typical length scale of the order of the Compton length
occurring at a typical length scale of the order of the Compton length ![]() that defines
that defines ![]() through D. The free parameter k fits the basic physical definition
through D. The free parameter k fits the basic physical definition ![]() of diffusion coefficient to the appropriate value in specific situations. Specifically, as it will be shown below, this result also implies regarding
of diffusion coefficient to the appropriate value in specific situations. Specifically, as it will be shown below, this result also implies regarding ![]() as the distance separating the surfaces of two bodies of matter: thinking for example to the black body, m can be the mass of a particle evaporated from the internal surface of the cavity and diffusing throughout the cavity, whose size
as the distance separating the surfaces of two bodies of matter: thinking for example to the black body, m can be the mass of a particle evaporated from the internal surface of the cavity and diffusing throughout the cavity, whose size ![]() is defined as a function of n.
is defined as a function of n.
From Equation (25) follow interesting consequences. Rewrite
![]() (26)
(26)
where ![]() is an arbitrary constant volume.
is an arbitrary constant volume.
Note that ![]() has physical dimensions time/mass; thus
has physical dimensions time/mass; thus ![]() is the particle mobility, also defined as velocity/force. Moreover
is the particle mobility, also defined as velocity/force. Moreover ![]() has physical dimensions force ´ length, i.e. pressure ´ volume.
has physical dimensions force ´ length, i.e. pressure ´ volume.
The dimensional analysis suggests that ![]() should be related to, and thus proportional to,
should be related to, and thus proportional to,![]() . Putting indeed
. Putting indeed ![]() and merging the proportionality constant with k of Equation (18), one finds concurrently three relevant results.
and merging the proportionality constant with k of Equation (18), one finds concurrently three relevant results.
First the well known law![]() ; of course this result holds for non interacting particles, as in the case of an ideal gas, whereas T is clearly linked to
; of course this result holds for non interacting particles, as in the case of an ideal gas, whereas T is clearly linked to ![]() previously found. With specific reference to the present model, the gas is that formed by evaporation of matter from the internal walls of the cavity containing the Planck radiation;
previously found. With specific reference to the present model, the gas is that formed by evaporation of matter from the internal walls of the cavity containing the Planck radiation; ![]() is related to the temperature of gas particles in equilibrium with the surface of the cavity.
is related to the temperature of gas particles in equilibrium with the surface of the cavity.
Moreover
![]() (27)
(27)
where C is the concentration of m in ![]() and
and ![]() is a constant. So the former equation is the well known Einstein equation linking diffusion coefficient and mobility.
is a constant. So the former equation is the well known Einstein equation linking diffusion coefficient and mobility.
Eventually, the third equation defines the chemical potential; this clarifies the physical meaning of ![]() and suggests the chance of identifying
and suggests the chance of identifying ![]() as the equilibrium uni- form concentration that implies
as the equilibrium uni- form concentration that implies ![]() in correspondence to
in correspondence to![]() , which indicates the end of the diffusion process.
, which indicates the end of the diffusion process.
In effect, the diffusion equations are contextually obtainable. Dividing both sides of Equation (25) by![]() , one finds
, one finds
![]()
i.e. this equation defines a force F acting on m. It is easy to convert force into mass flux J, having physical dimensions of mass per unit time and surface, dividing both sides by![]() . Recalling that by definition
. Recalling that by definition![]() , this equation reads
, this equation reads
![]()
This is the well known Fick diffusion law, from which also follows the second Fick law with the help of an appropriate continuity equation that excludes mass sinks or sources within![]() . Given a function
. Given a function![]() , its differential
, its differential
![]()
subjected to the condition ![]() reads
reads ![]() with
with![]() ; so with vector notation
; so with vector notation![]() . Putting by definition
. Putting by definition![]() , where G is an arbitrary vector to be specified, the result
, where G is an arbitrary vector to be specified, the result ![]() yields
yields ![]() once having put
once having put![]() . The solenoidal character of the velocity vector excludes sinks or sources of matter crossing from inside or outside the surface of an ideal flux pipe around v. Also, it is clearly convenient to identify the arbitrary vector G with the flux vector J and thus
. The solenoidal character of the velocity vector excludes sinks or sources of matter crossing from inside or outside the surface of an ideal flux pipe around v. Also, it is clearly convenient to identify the arbitrary vector G with the flux vector J and thus![]() . If so, then
. If so, then ![]() yields the component
yields the component
![]()
i.e. the definition of mass flux and the one dimensional second Fick law.
Eventually, Equation (26) reads with the help of Equations (3) and (27) as follows
![]()
Suppose now that m is the j-th mass in a system constituted of a number ![]() of masses, i.e. actually it is regarded here as
of masses, i.e. actually it is regarded here as![]() . Next sum up this equation over j, i.e. over all masses of the system; one finds thus
. Next sum up this equation over j, i.e. over all masses of the system; one finds thus
![]()
Since by definition![]() , assuming
, assuming ![]() independent of the index j one finds
independent of the index j one finds
![]()
This equation defines the entropy S a function ![]() apart as
apart as
![]()
note that ![]() is not necessarily constant, simply it does not depend upon j, e.g. it can depend on T or pressure and so on. So at constant T one finds
is not necessarily constant, simply it does not depend upon j, e.g. it can depend on T or pressure and so on. So at constant T one finds![]() . These contextual results show that the driving force of the Fick laws is the entropy increase, i.e. the second principle of the thermodynamics.
. These contextual results show that the driving force of the Fick laws is the entropy increase, i.e. the second principle of the thermodynamics.
All this is linked to the further information provided by Equation (25). Noting that![]() , this equation yields
, this equation yields
![]() (28)
(28)
this equation relates ![]() to
to![]() ; depending on the sign of this latter, one can have mass fluctuations corresponding to
; depending on the sign of this latter, one can have mass fluctuations corresponding to![]() , to which is related the energy fluctuation
, to which is related the energy fluctuation![]() . If in particular
. If in particular![]() , then
, then ![]() implies
implies![]() . It appears that the energy fluctuation
. It appears that the energy fluctuation ![]() of the radiation is linked to the evaporation or deposition rates
of the radiation is linked to the evaporation or deposition rates ![]() of matter on or from the contact wall; their relative balance determines the increasing or decreasing amount of mass in the cavity correspondingly to the concurring oscillations of
of matter on or from the contact wall; their relative balance determines the increasing or decreasing amount of mass in the cavity correspondingly to the concurring oscillations of![]() . Eventually note that the left hand side of Equation (28) defines the energy
. Eventually note that the left hand side of Equation (28) defines the energy ![]() to which contribute not only the radiation but also the matter through its evaporation rate
to which contribute not only the radiation but also the matter through its evaporation rate![]() . This conclusion automatically includes the interaction between photon and solid matter, without excluding of course that of photons with gas particles evaporated from the surface. Moreover the model provides thermodynamic information able to describe both the equilibrium state of the system and its transient deviation during its fluctuation.
. This conclusion automatically includes the interaction between photon and solid matter, without excluding of course that of photons with gas particles evaporated from the surface. Moreover the model provides thermodynamic information able to describe both the equilibrium state of the system and its transient deviation during its fluctuation.
Combine now Equations (24) and (6) to eliminate v; as ![]() owing to Equation (4) and thus
owing to Equation (4) and thus
![]()
the result is
![]()
So
![]() (29)
(29)
Put preliminarily![]() , i.e. neglect the first and second order terms of Equation (23); this equation reduces to
, i.e. neglect the first and second order terms of Equation (23); this equation reduces to ![]() and reads then
and reads then
![]() (30)
(30)
Equations (29) and (30) concern both arbitrary square energies, a scale factor apart for the three quantities characterizing the initial ![]() and p of Equation (6), and thus are physically equivalent provided that
and p of Equation (6), and thus are physically equivalent provided that![]() ; this requires of course
; this requires of course ![]() and implies an appropriate scale factor that converts the initial m to
and implies an appropriate scale factor that converts the initial m to![]() . In effect the variables of the problem are three, i.e
. In effect the variables of the problem are three, i.e![]() , m and v, i.e. n; whatever the specific value of
, m and v, i.e. n; whatever the specific value of ![]() might be, the constrains of these positions are three as well, i.e. the factors linking the last three equations. It is worth noticing that if
might be, the constrains of these positions are three as well, i.e. the factors linking the last three equations. It is worth noticing that if ![]() for
for![]() , then
, then ![]() by definition. Since this conclusion holds even if referred in particular to different coordinate systems in reciprocal constant motion, this shows that these equations represent invariant expressions of energy.
by definition. Since this conclusion holds even if referred in particular to different coordinate systems in reciprocal constant motion, this shows that these equations represent invariant expressions of energy.
Consider now that in Equation (29)
![]()
this term having the form ![]() with
with ![]() is a well known result of quantum gravity, which solves three cosmological paradoxes [8] . In conclusion, combining the zero order approximation of Equation (23) with Equation (6) one finds the classical expression of relativistic energy; the additional first order term accounts for the quantum correction of the rest energy
is a well known result of quantum gravity, which solves three cosmological paradoxes [8] . In conclusion, combining the zero order approximation of Equation (23) with Equation (6) one finds the classical expression of relativistic energy; the additional first order term accounts for the quantum correction of the rest energy ![]() of cosmological significance. The Section 7 will show that actually even this result is not accidental.
of cosmological significance. The Section 7 will show that actually even this result is not accidental.
The fact that ![]() fits the physical meaning of the literature result stimulates a further idea. As
fits the physical meaning of the literature result stimulates a further idea. As ![]() according to Equation (3), Equation (23) yields at the first order
according to Equation (3), Equation (23) yields at the first order
![]()
in effect ![]() is compatible with
is compatible with![]() . The form
. The form ![]() suggests that v and
suggests that v and ![]() could be, at least approximately, velocity components expressed in different reference systems. Is thus attracting the idea of implementing
could be, at least approximately, velocity components expressed in different reference systems. Is thus attracting the idea of implementing ![]() to define
to define ![]() and then
and then ![]() in analogy with Equation (3) but in a different reference system. Moreover admit for generality that
in analogy with Equation (3) but in a different reference system. Moreover admit for generality that ![]() and
and ![]() depend on new mass
depend on new mass ![]() and frequency
and frequency![]() ; thus, differentiating
; thus, differentiating ![]() exactly as before to infer Equation (21), one finds
exactly as before to infer Equation (21), one finds
![]()
In effect ![]() has no peculiarity with respect to v previously introduced; both are arbitrary velocities, both fulfill the same kind of connection between
has no peculiarity with respect to v previously introduced; both are arbitrary velocities, both fulfill the same kind of connection between ![]() and E. If this reasoning is correct, then even this result must have a sensible physical meaning. The check is again carried out solving this primed differential equation. One finds
and E. If this reasoning is correct, then even this result must have a sensible physical meaning. The check is again carried out solving this primed differential equation. One finds
![]()
and thus
![]()
Since ![]() is momentum, this result reads
is momentum, this result reads
![]() (31)
(31)
i.e. is admissible Equation (21) with the right hand side having the form ![]() instead of the definition (23) of
instead of the definition (23) of![]() . In fact, this conclusion is still compatible with Equation (23) itself simply putting
. In fact, this conclusion is still compatible with Equation (23) itself simply putting ![]() as a particular case in an appropriate reference system. It is instructive to obtain this last result even through a different reasoning.
as a particular case in an appropriate reference system. It is instructive to obtain this last result even through a different reasoning.
Calculate via the second Equation (6)
![]()
Split this equation putting by definition
![]() (32)
(32)
The second position, allowed in principle by dimensional reasons, allows to handle the first equation as follows with the help of the first Equation (6)
![]()
Note that there is no reference to ![]() in this last result, which instead relates the changes of p and
in this last result, which instead relates the changes of p and ![]() to
to ![]() of the energy. Assume therefore that these changes are due to
of the energy. Assume therefore that these changes are due to ![]() and not to
and not to![]() . In this case, the first Equation (6) yields
. In this case, the first Equation (6) yields
![]() (33)
(33)
This result is confirmed by the second Equation (32), which yields with the help of the third Equation (6)
![]()
this equation reads ![]() and is easily integrated. The result is
and is easily integrated. The result is
![]() (34)
(34)
being ![]() the integration constant. It appears that putting
the integration constant. It appears that putting ![]() the result coincides with that previously found, despite here has been considered the dependence of p and
the result coincides with that previously found, despite here has been considered the dependence of p and ![]() on v. It is easy to realize that only the positions (32) allow a consistent calculation of
on v. It is easy to realize that only the positions (32) allow a consistent calculation of ![]() in Equations (33) and (34); for instance, replacing Equation (32) with the
in Equations (33) and (34); for instance, replacing Equation (32) with the ![]() and
and![]() , in principle also possible because
, in principle also possible because ![]() is dimen- sionless, would imply inconsistent expressions of
is dimen- sionless, would imply inconsistent expressions of![]() . This conclusion agrees with the result of Equation (31).
. This conclusion agrees with the result of Equation (31).
It appears in conclusion that the term ![]() is enough for the purposes of the present model, while it is confirmed that the zero order term of the series (23) accounts for “classical” relativistic results.
is enough for the purposes of the present model, while it is confirmed that the zero order term of the series (23) accounts for “classical” relativistic results.
Implement then Equation (21) in the simplest form
![]() (35)
(35)
Comparing with Equation (19), ![]() is nothing else but anyone among the possible values of
is nothing else but anyone among the possible values of![]() . Therefore, the third equation of the problem that regards separately
. Therefore, the third equation of the problem that regards separately ![]() and
and ![]() reads
reads
![]() (36)
(36)
the physical meaning of this equation is to consider the averages of all possible ![]() and
and ![]() compatible with the given E and
compatible with the given E and![]() ; in effect the arbitrary changes
; in effect the arbitrary changes ![]() and
and ![]() are independent of the respective E and
are independent of the respective E and![]() , as already remarked.
, as already remarked.
In conclusion, to the four variables appearing in (17) correspond three Equations (3), (21) and (36); the free parameter k introduced in (18) is a freedom degree of the problem as a function of which are in principle determinable various E, m and v, i.e. n.
These results have been hitherto obtained without specific reference to the black body cavity and even regardless of the Planck formula. The next section concerns just this topic.
5. The Black Body
To specify the previous results in the case of radiation in a black body cavity of arbitrary volume V, it is useful to consider first the Planck law. Noting that this law reads
![]()
let us examine the three factors that define![]() .
.
The degeneracy factor 2 of the Bose statistical distribution of photons with the same energy corresponds to the orthogonal polarizations of light [9] , to which is due the usual elliptic polarization of a light beam of frequency![]() .
.
The factor ![]() suggests an integration over a solid angle
suggests an integration over a solid angle![]() . The physical meaning of this statement is clarified below. It is anticipated here that the integral concerns the random impacts of photons on various points of the internal surface of the cavity because of multiple reflections; accordingly any element of this surface thermalizes the radiation trapped inside V.
. The physical meaning of this statement is clarified below. It is anticipated here that the integral concerns the random impacts of photons on various points of the internal surface of the cavity because of multiple reflections; accordingly any element of this surface thermalizes the radiation trapped inside V.
The notation ![]() of the number density of photons with frequency
of the number density of photons with frequency ![]() emphasizes that just the wavelength
emphasizes that just the wavelength ![]() defines the volume
defines the volume ![]() enclosing a cluster of
enclosing a cluster of ![]() photons with the same frequency
photons with the same frequency![]() , whereas instead the true volume V of the cavity is seemingly irrelevant; it is replaced by the local volume defined by the cluster of photons themselves, supposed of course non-interacting at the usual temperatures at which is modeled and tested the black body radiation law. Also this crucial point is concerned below.
, whereas instead the true volume V of the cavity is seemingly irrelevant; it is replaced by the local volume defined by the cluster of photons themselves, supposed of course non-interacting at the usual temperatures at which is modeled and tested the black body radiation law. Also this crucial point is concerned below.
With these hints, is really easy to infer the Planck result even in the present physical frame only.
First of all, ![]() is found implementing once more Equations (26) and (27). Integrate Equation (26) with the help of Equation (27) between two arbitrary energies
is found implementing once more Equations (26) and (27). Integrate Equation (26) with the help of Equation (27) between two arbitrary energies ![]() and
and![]() ; one finds
; one finds![]() . It is possible to write
. It is possible to write![]() , because in principle C can be greater or lower than the constant
, because in principle C can be greater or lower than the constant ![]() of interest for the present reasoning; then this last equation reads
of interest for the present reasoning; then this last equation reads![]() . Of course
. Of course ![]() and
and ![]() are referred to the same arbitrary volume
are referred to the same arbitrary volume![]() ; more- over the masses
; more- over the masses ![]() and
and ![]() are proportional to the respective numbers
are proportional to the respective numbers ![]() and
and ![]() of particles, as they refer to a unique material or kind of particle. Hence one finds with these positions
of particles, as they refer to a unique material or kind of particle. Hence one finds with these positions
![]() (37)
(37)
Note that ![]() has the same form of
has the same form of ![]() of Equation (27) a constant
of Equation (27) a constant ![]() apart, i.e. it is chemical potential. This result is nothing else but the well known statistical distribution of bosons and fermions as a function of the energy; their occupancy numbers of quantum states are inferable in general from the respective profiles as a function of temperature for either sign, instead of being postulated “a priori”.
apart, i.e. it is chemical potential. This result is nothing else but the well known statistical distribution of bosons and fermions as a function of the energy; their occupancy numbers of quantum states are inferable in general from the respective profiles as a function of temperature for either sign, instead of being postulated “a priori”.
This point does not need further comments. Here, with the minus sign and putting![]() , one calculates the Planck equation.
, one calculates the Planck equation.
The number density ![]() is calculated via a variable volume
is calculated via a variable volume ![]() dependent upon the wavelengths allowed in the cavity compatibly with the fixed real volume V.
dependent upon the wavelengths allowed in the cavity compatibly with the fixed real volume V.
Let the cavity contain ![]() photons of frequency
photons of frequency ![]() that define the energy density
that define the energy density ![]() in the physical volume
in the physical volume![]() ; then
; then
![]() (38)
(38)
where clearly ![]() is in general anyone of the
is in general anyone of the ![]() frequencies allowed in the cavity. In this equation, the wavelength is regarded as measure unit to express the size of each
frequencies allowed in the cavity. In this equation, the wavelength is regarded as measure unit to express the size of each![]() , which in this way results consistent by definition with the existence of standing waves. Moreover the obvious condition
, which in this way results consistent by definition with the existence of standing waves. Moreover the obvious condition
![]() (39)
(39)
is fulfilled because V has not yet been specified. Whatever V might be, the sum over the various ![]() can be replaced by that over an arbitrary real number n via the position
can be replaced by that over an arbitrary real number n via the position![]() , being
, being ![]() the lowest frequency allowed in a cavity of size
the lowest frequency allowed in a cavity of size![]() . If the various
. If the various ![]() are very close each other, then n can be regarded as a continuous variable; if so, the sum can be replaced by an integral between
are very close each other, then n can be regarded as a continuous variable; if so, the sum can be replaced by an integral between![]() , in order to include
, in order to include![]() , and an arbitrary
, and an arbitrary![]() .
.
In this case one would find![]() ; the notation emphasizes that replacing sum with integral implies a numerical approximation. Despite this result fulfills the obvious requirements of increasing and finite V for
; the notation emphasizes that replacing sum with integral implies a numerical approximation. Despite this result fulfills the obvious requirements of increasing and finite V for![]() , one would expect
, one would expect![]() : by definition, indeed,
: by definition, indeed, ![]() is the volume
is the volume ![]() pertinent to the lowest frequency only. Moreover if
pertinent to the lowest frequency only. Moreover if ![]() would be plain real number, the limit
would be plain real number, the limit ![]() would yield
would yield![]() ; so the energy
; so the energy ![]() inside the cavity should vanish, unless admitting
inside the cavity should vanish, unless admitting![]() . These inconsistencies, not merely numerical but physical, can be due to nothing else but to the low values of n contributing to the sum badly approximated by the integration; indeed it is true that
. These inconsistencies, not merely numerical but physical, can be due to nothing else but to the low values of n contributing to the sum badly approximated by the integration; indeed it is true that ![]() behaves in fact like a continuous variable. In effect the contribution of the low values of n is underestimated by the integration. Examine therefore the chance that n can take integer values only: in this case one finds
behaves in fact like a continuous variable. In effect the contribution of the low values of n is underestimated by the integration. Examine therefore the chance that n can take integer values only: in this case one finds ![]() even for the lowest
even for the lowest![]() , whereas
, whereas ![]() for
for![]() . Also, V remains anyway finite because n cannot longer approach arbitrarily to 1.
. Also, V remains anyway finite because n cannot longer approach arbitrarily to 1.
It is known in effect that the steady wavelengths ![]() allowed within a range
allowed within a range ![]() must fulfill the condition
must fulfill the condition
![]() (40)
(40)
with n integer; in other words, the electric field of an electromagnetic wave must vanish at the boundaries of its physical volume of confinement, correspondingly to wave nodes at the boundaries.
The seemingly innocuous position (39) implies thus the energy quantization in the cavity. Equations (2) and (3) yield indeed
![]()
i.e. ![]() and
and ![]() and so on for all
and so on for all ![]() allowed in the cavity once regarding
allowed in the cavity once regarding ![]() as its size. If the photons are assumed non-interacting at the usual T of interest for the black body physics, the sum (38) consists of independent terms. Considering one of these terms,
as its size. If the photons are assumed non-interacting at the usual T of interest for the black body physics, the sum (38) consists of independent terms. Considering one of these terms, ![]() , and differentiating it, one finds at the first order
, and differentiating it, one finds at the first order
![]() (41)
(41)
thus
![]() (42)
(42)
To highlight the physical meaning of the differentials ![]() and
and![]() , implement this equation to calculate the energy density per unit range
, implement this equation to calculate the energy density per unit range![]() , i.e.
, i.e.
![]() (43)
(43)
All frequencies allowed in the cavity contribute to ![]() according to Equation (41), whereas Equation (43) selects some frequencies in the range
according to Equation (41), whereas Equation (43) selects some frequencies in the range![]() : i.e.
: i.e. ![]() is an energy density per unit frequency range. All addends share the number density
is an energy density per unit frequency range. All addends share the number density ![]() of a cluster of photons with the same frequency; regard thus this ratio as characteristic property of the cluster. Consider now that the thermal equilibrium inside the cavity requires the exchange of energy between the various
of a cluster of photons with the same frequency; regard thus this ratio as characteristic property of the cluster. Consider now that the thermal equilibrium inside the cavity requires the exchange of energy between the various ![]() existing in the cavity. Since however the photons of each cluster have been assumed non-interacting, this exchange cannot be that between different clusters; hence the thermalizing interaction can be nothing else but that with the cavity surface enclosing all photon clusters and possibly with the gas matter evaporated from the walls of the cavity. This fact suggests that the equation
existing in the cavity. Since however the photons of each cluster have been assumed non-interacting, this exchange cannot be that between different clusters; hence the thermalizing interaction can be nothing else but that with the cavity surface enclosing all photon clusters and possibly with the gas matter evaporated from the walls of the cavity. This fact suggests that the equation
![]() (44)
(44)
defines the radiation energy density per unit frequency ![]() at the thermal equilibrium with the whole internal surface of the cavity; the corresponding
at the thermal equilibrium with the whole internal surface of the cavity; the corresponding ![]() represents instead the local interaction of each cluster of photons per unit solid angle, i.e. with any elementary surface element
represents instead the local interaction of each cluster of photons per unit solid angle, i.e. with any elementary surface element![]() . In effect the integral represents by definition the sum of all local interactions
. In effect the integral represents by definition the sum of all local interactions ![]() of the photon cluster with elementary elements
of the photon cluster with elementary elements ![]() of internal surface of the cavity; this supports the idea of regarding
of internal surface of the cavity; this supports the idea of regarding ![]() as a local quantity and
as a local quantity and ![]() as an average global quantity. In other words, the integral corresponds to and represents the cumulative effect of all internal reflections of each photon cluster consistent with the physical model of black body cavity. This is equivalent to say that
as an average global quantity. In other words, the integral corresponds to and represents the cumulative effect of all internal reflections of each photon cluster consistent with the physical model of black body cavity. This is equivalent to say that ![]() concerns the local thermal equilibrium of the photon cluster with one arbitrary surface element
concerns the local thermal equilibrium of the photon cluster with one arbitrary surface element ![]() only,
only, ![]() represents the complete thermal equilibrium after interaction of the cluster with the whole surface of the cavity. So
represents the complete thermal equilibrium after interaction of the cluster with the whole surface of the cavity. So ![]() and
and ![]() differ numerically because of the amount of corresponding energy density exchanged between radiation and surface.
differ numerically because of the amount of corresponding energy density exchanged between radiation and surface.
If Equation (44) leads to the correct formulation of the Planck law, then it also proofs indirectly that the photon thermalization mechanism occurs at the surface of the cavity.
The integration of ![]() is immediate admitting that the interaction process is isotropic, i.e. the energy exchange occurs uniformly for all frequencies and that any allowed
is immediate admitting that the interaction process is isotropic, i.e. the energy exchange occurs uniformly for all frequencies and that any allowed ![]() is not appreciably perturbed by the small energy loss; being the radiation field at the equilibrium uniformly distributed inside the cavity, there is no dependence of
is not appreciably perturbed by the small energy loss; being the radiation field at the equilibrium uniformly distributed inside the cavity, there is no dependence of ![]() upon the arbitrary direction along which is defined
upon the arbitrary direction along which is defined![]() . So the result of the integration is simply
. So the result of the integration is simply![]() . Equation (43) yields therefore the following energy density per unit frequency thermalized by all possible paths of the n-th cluster of photons in the cavity:
. Equation (43) yields therefore the following energy density per unit frequency thermalized by all possible paths of the n-th cluster of photons in the cavity:
![]() (45)
(45)
Noting that
![]()
Equation (45) reads then
![]() (46)
(46)
This expression can be considerably simplified because
![]()
has a maximum as a function of![]() , which suggests
, which suggests ![]() for an appropriate value
for an appropriate value ![]() of the
of the ![]() -th frequency. In this case the second addend of Equation (45) vanishes for this particular value
-th frequency. In this case the second addend of Equation (45) vanishes for this particular value![]() . Hence, replacing
. Hence, replacing ![]() in Equation (37) to account for the light polarization states with the same
in Equation (37) to account for the light polarization states with the same ![]() in the Bose function and calculating Equation (46) with
in the Bose function and calculating Equation (46) with![]() , the result at
, the result at ![]() is simply
is simply
![]() (47)
(47)
Therefore, the plain Planck law corresponds to the particular set of frequencies that, among the ones allowed in the cavity, maximize the number density of photons with a given energy at a fixed T.
Actually, however, no physical reason requires ![]() and T really constant; nevertheless, the analytical form of the first addend of Equation (46) is identical to that of
and T really constant; nevertheless, the analytical form of the first addend of Equation (46) is identical to that of ![]() in Equation (47). This suggests that
in Equation (47). This suggests that ![]() is still given in general by the first addend of Equation (46) even though calculated with a frequency
is still given in general by the first addend of Equation (46) even though calculated with a frequency ![]() and thus without the constrain on T that annul the other terms; these terms account therefore for the frequency and temperature fluctuations with respect to the zero order term represented by the Planck function. This conclusion clarifies that
and thus without the constrain on T that annul the other terms; these terms account therefore for the frequency and temperature fluctuations with respect to the zero order term represented by the Planck function. This conclusion clarifies that ![]() and
and ![]() represent just the frequency and temperature fluctuations of the cavity.
represent just the frequency and temperature fluctuations of the cavity.
In the present model it appears therefore that:
・ The interaction between degenerate photon clusters and internal walls of the cavity is responsible for the thermalization mechanism.
・ The fluctuations are inferred contextually to the Planck law itself.
To emphasize these points, it is necessary now to link these fluctuations with Equations (19) and (20). As expected, the fluctuation is given by temperature and frequency deviations of ![]() with respect to the mere equilibrium Planck term; simple considerations show indeed that the fluctuation terms can have in principle positive or negative sign.
with respect to the mere equilibrium Planck term; simple considerations show indeed that the fluctuation terms can have in principle positive or negative sign.
Now it is possible to tackle the problem of describing the cavity for ![]() and
and![]() , i.e. when both frequency and temperature are allowed to fluctuate.
, i.e. when both frequency and temperature are allowed to fluctuate.
6. Black Body Fluctuation
The result (25) and Equation (44) imply the involvement of the material constituting the wall of the cavity to reach the condition of thermodynamic equilibrium of photons therein confined. In particular ![]() appears related to
appears related to ![]() and
and![]() , i.e. to the material evaporating from the internal surface of the shell and present in the cavity together with the radiation field. This is confirmed by the mean square velocity
, i.e. to the material evaporating from the internal surface of the shell and present in the cavity together with the radiation field. This is confirmed by the mean square velocity ![]() of matter particles present in gas phase in the cavity contextually inferred. It is known from the elementary kinetic theory of gases that
of matter particles present in gas phase in the cavity contextually inferred. It is known from the elementary kinetic theory of gases that ![]() is related to
is related to![]() . Even though the photons are admitted non-interacting, their thermalization process occurs by interaction both with the internal wall of the cavity and with the amount of matter expectedly evaporated and trapped in the cavity together with the radiation itself; clearly the gas phase is at the thermal equilibrium with the cavity wall.
. Even though the photons are admitted non-interacting, their thermalization process occurs by interaction both with the internal wall of the cavity and with the amount of matter expectedly evaporated and trapped in the cavity together with the radiation itself; clearly the gas phase is at the thermal equilibrium with the cavity wall.
For sake of clarity, collect together Equations (3), (27) and (25); one finds
![]() (48)
(48)
These equations evidence in particular
![]() (49)
(49)
whereas Equation (19) reads
![]() (50)
(50)
Since k has been defined as a mean value in Equation (18), let then be
![]()
being q an arbitrary constant. Then, Equation (36) yields
![]()
Since Equation (49) reads
![]()
so that merging these equations one finds
![]() (51)
(51)
the result obtained via Equation (50) is
![]()
Therefore
![]()
yields
![]() (52)
(52)
hence
![]() (53)
(53)
As![]() , this is just the famous Einstein equation [10] . To find this result, Einstein quoted the energy of a sub-volume enclosed by a large volume, both concurring to the total volume of the cavity and exchanging energy. Here the role of the smaller volume is proportional to
, this is just the famous Einstein equation [10] . To find this result, Einstein quoted the energy of a sub-volume enclosed by a large volume, both concurring to the total volume of the cavity and exchanging energy. Here the role of the smaller volume is proportional to![]() , whose fluctuation is the source function of the Einstein model of a closed system. Actually this appears in Equation (44), because the photons are thermalized just impacting against the wall of the cavity, which is therefore the effective source of the photon energy. So it appears clearly that the fluctuations are controlled by the matter constituting the walls of the cavity; this conclusion has been in effect assumed in the paper [5] . If in fact
, whose fluctuation is the source function of the Einstein model of a closed system. Actually this appears in Equation (44), because the photons are thermalized just impacting against the wall of the cavity, which is therefore the effective source of the photon energy. So it appears clearly that the fluctuations are controlled by the matter constituting the walls of the cavity; this conclusion has been in effect assumed in the paper [5] . If in fact![]() , then
, then![]() : i.e. the average energy is controlled by the matter at the walls of the cavity. Consistently
: i.e. the average energy is controlled by the matter at the walls of the cavity. Consistently ![]() is also related itself to the radiation field
is also related itself to the radiation field![]() , as it appears in Equation (52). Clearly it is reasonable to put here
, as it appears in Equation (52). Clearly it is reasonable to put here
![]()
Replacing Equations (51) into (53), one finds
![]() (54)
(54)
According to the previous considerations, ![]() for
for![]() ; this confirms that the left hand side of Equation (54) is a fluctuation energy. Equation (51) yields then the relationship between frequency and temperature fluctuations
; this confirms that the left hand side of Equation (54) is a fluctuation energy. Equation (51) yields then the relationship between frequency and temperature fluctuations
![]() (55)
(55)
7. Discussion
The fluctuations are likely the most typical manifestation of the probabilistic character of the quantum world, while also being the most striking evidence of the quantum uncertainty. Nevertheless, elementary and straightforward considerations have shown that the equations describing the fluctuations are also compliant with relativistic corollaries: both have been concurrently inferred from Equation (1) in a unique theoretical frame. Despite the deterministic character of the relativity, the results so far outlined emphasize this seemingly surprising connection. Actually a similar conclusion was already found also in [7] implementing an operative definition of space time, i.e. introducing ab initio the quantity ![]() as a basic postulate to be handled subsequently likewise any fundamental physical law.
as a basic postulate to be handled subsequently likewise any fundamental physical law.
First of all, the present model plugs the problem of the black body radiation and its fluctuations in a wide context of physical laws having prospective interest for the non-equilibrium physics. The quantum basis of the Fick law is important because various physical properties, e.g. the heat and electrical conductivities, have analogous form; here, in particular, the diffusion equations are in principle necessary to account for the unstable concentration gradients reasonably expected in gas phase due to random concentration fluctuations of the matter evaporated from the internal surface of the cavity. In effect the dynamics of matter particles that diffuse from the walls of the cavity contributes to the thermalization process; in this respect, the model introduces concurrently even the free energy and entropy concepts useful to infer the Clausius-Clapeyron equation governing the vapor pressure and thus the amount of matter in gas phase filling the cavity together with the radiation. In view of that, the Planck law has been inferred in order to involve since the beginning the solid matter confining the photons and even their energy quantization and statistical distribution law. The interaction of photons with matter appears in fact essential to justify the thermalization mechanism. Strictly speaking, the radiation with wavelength larger than the finite size cavity should not be consistent with the standard approach to the Planck law; here however this problem is bypassed since the cavity volume V is not predetermined, rather it is determined by the radiation wavelengths themselves via the terms (39). Thus it is by definition compliant with the arbitrary size ![]() defining the allowed frequencies according to Equations (1), (2) and (38). For these reasons, is reductive the model [10] focused on the radiation field in the cavity only.
defining the allowed frequencies according to Equations (1), (2) and (38). For these reasons, is reductive the model [10] focused on the radiation field in the cavity only.
The black body radiation field and its fluctuations have been contextually inferred merging two separate paths: the one from Equations (14) to (20) is apparently independent on that leading from Equation (45) to Equation (53). The former series of equations does not refer specifically to the black body radiation, it introduces relationships between changes of dynamical variables that hold in general. The latter series of equations describes specifically the black body radiation under the boundary condition of Equation (20), which also implies Equations (21) to (24); this second path links the frequency and mass fluctuations, in agreement with Equations (4) to (9). Then, Equation (36) introduces the thermal equilibrium of Equation (50) leading to Equation (53).
Yet other significant results are also easily inferable from the previous considerations of the Section 4.
For example, combining Equations (26) and (27) with Equation (28) one finds at constant T
![]()
The equation ![]() is easily integrated; calling
is easily integrated; calling ![]() the integration constant, the solution
the integration constant, the solution
![]()
yields
![]()
Owing to the first Equation (27) put then
![]()
being ![]() a constant diffusion coefficient corresponding to the integration constant
a constant diffusion coefficient corresponding to the integration constant![]() . The conclusion is
. The conclusion is
![]()
This Arrhenius-like equation is a well known property of the diffusion coefficient, whose quantum origin introduces the activation energy as a consequence.
Other important equations of processes activated by the temperature follow this kind of dependence upon![]() .
.
A further significant result is obtained from Equation (6), assuming that the momentum p is time dependent variable. This compels regarding the wavelength ![]() as time variable itself, as in effect it is possible because no restrictive hypothesis has been introduced about p and thus about
as time variable itself, as in effect it is possible because no restrictive hypothesis has been introduced about p and thus about ![]() in Equations (2) and (4). Deriving thus
in Equations (2) and (4). Deriving thus ![]() with respect to time in the reference system R previously introduced to define
with respect to time in the reference system R previously introduced to define ![]() and
and ![]() of Equation (2), one finds
of Equation (2), one finds
![]() (56)
(56)
It is possible to expand in series ![]() around an arbitrary constant value
around an arbitrary constant value![]() , e.g.
, e.g.
![]() (57)
(57)
being ![]() appropriate coefficients. Implement Equation (40) to express again length
appropriate coefficients. Implement Equation (40) to express again length ![]() as a function of wavelength
as a function of wavelength![]() ; here, however,
; here, however, ![]() is the momentum wavelength of Equation (5). To highlight the physical meaning of the series expansion, retain preliminarily the constant term only and consider two chances of rewriting the first Equation (56). Eliminate h from Equation (56), replacing it via the Planck mass
is the momentum wavelength of Equation (5). To highlight the physical meaning of the series expansion, retain preliminarily the constant term only and consider two chances of rewriting the first Equation (56). Eliminate h from Equation (56), replacing it via the Planck mass ![]() and fine structure constant
and fine structure constant![]() ; so, being by definition
; so, being by definition
![]() (58)
(58)
Equation (56) reads at the zero order of approximation of the series expansion according to Equation (40)
![]() (59)
(59)
Since F is actually the component of a force along![]() , which can have both signs, consider for brevity of notation its absolute value only. This expression reads then
, which can have both signs, consider for brevity of notation its absolute value only. This expression reads then
![]() (60)
(60)
having put
![]()
As n and ![]() are arbitrary, likewise the primed and double primed quantities, these approximate definitions of force correspond to the Newton and Coulomb interactions between arbitrary masses and steady charges, which have thus analogous form. In effect, at this level of approximation, neither term of the equality (60) depends on v. The only term that could introduce charge velocity is
are arbitrary, likewise the primed and double primed quantities, these approximate definitions of force correspond to the Newton and Coulomb interactions between arbitrary masses and steady charges, which have thus analogous form. In effect, at this level of approximation, neither term of the equality (60) depends on v. The only term that could introduce charge velocity is![]() ; yet no reason requires assuming
; yet no reason requires assuming![]() . In lack of specific hypotheses, therefore,
. In lack of specific hypotheses, therefore, ![]() is consistent with stationary charges. In the case of gravity force, it is well known that the Newton law is generalized by the general relativity; it is reasonable therefore to expect that the terms of series expansions, here neglected preliminarily, account for the necessary relativistic corrections of the plain Newton law. To demonstrate this statement, calculate via Equation (56) the potential energy U generated by the mass m defining p at any point
is consistent with stationary charges. In the case of gravity force, it is well known that the Newton law is generalized by the general relativity; it is reasonable therefore to expect that the terms of series expansions, here neglected preliminarily, account for the necessary relativistic corrections of the plain Newton law. To demonstrate this statement, calculate via Equation (56) the potential energy U generated by the mass m defining p at any point![]() ; the subscript emphasizes that
; the subscript emphasizes that ![]() concerns the radial distance of
concerns the radial distance of ![]() from
from![]() . As by de- finition
. As by de- finition![]() , Equations (56) and (57) yield
, Equations (56) and (57) yield
![]() (61)
(61)
Whatever the value of ![]() might be, depending on the series coefficients
might be, depending on the series coefficients![]() , is remarkable the fact that the potential here inferred differs from the Newtonian form just because of the presence of terms neglected in the classical Equations (59) and (60). It is well known that the perihelion precession of orbiting bodies is correctly calculated in the general relativity by potential terms additional to the mere
, is remarkable the fact that the potential here inferred differs from the Newtonian form just because of the presence of terms neglected in the classical Equations (59) and (60). It is well known that the perihelion precession of orbiting bodies is correctly calculated in the general relativity by potential terms additional to the mere![]() , which however cannot be justified in the plain Newton model [11] . Here, in effect, additional terms appear as a natural consequence of
, which however cannot be justified in the plain Newton model [11] . Here, in effect, additional terms appear as a natural consequence of ![]() of Equation (56): there is no reason to assume that
of Equation (56): there is no reason to assume that ![]() be equal to the constant
be equal to the constant ![]() only, being instead reasonably expectable a more general form like that of Equation (57). Actually it is easy to show that U cannot be equal uniquely to the first addend; owing to Equation (60) one would infer indeed
only, being instead reasonably expectable a more general form like that of Equation (57). Actually it is easy to show that U cannot be equal uniquely to the first addend; owing to Equation (60) one would infer indeed
![]() (62)
(62)
in the mere Newtonian approximation of Equation (59). If so, however, the ratios ![]() and
and ![]() in principle arbitrary likewise
in principle arbitrary likewise![]() , could admit
, could admit![]() , which is however impossible. So a correction term, i.e.
, which is however impossible. So a correction term, i.e.![]() , is necessary to define U by comparing Equations (56) and (61). This conclusion confirms therefore that the terms of the sum (57), neglected for simplicity in Equation (60), are in fact essential to agree with the finite light speed and have thus relativistic valence.
, is necessary to define U by comparing Equations (56) and (61). This conclusion confirms therefore that the terms of the sum (57), neglected for simplicity in Equation (60), are in fact essential to agree with the finite light speed and have thus relativistic valence.
It is possible to show the validity of these conclusions, which should hold for the Coulomb law as well, by demonstrating how to find well known results of the general relativity as a consequence of Equation (19).
To this purpose it is necessary to generalize what ![]() actually means in
actually means in![]() . The previous considerations about the black body cavity have emphasized that
. The previous considerations about the black body cavity have emphasized that ![]() concerns the material evaporated from the internal walls of the cavity; as the temperature fluctuation modifies the vapor pressure of the cavity material,
concerns the material evaporated from the internal walls of the cavity; as the temperature fluctuation modifies the vapor pressure of the cavity material, ![]() refers to the change of amount of material evaporating from or condensing on the internal wall of the cavity according to the Clausius-Clapeyron equation. However the mass fluctuation can have a more general meaning, directly related to the concept of energy quantum fluctuation
refers to the change of amount of material evaporating from or condensing on the internal wall of the cavity according to the Clausius-Clapeyron equation. However the mass fluctuation can have a more general meaning, directly related to the concept of energy quantum fluctuation ![]() itself; e.g. it is possible in principle that
itself; e.g. it is possible in principle that![]() . Of course this effect is reasonably negligible in the case of a black body cavity, owing to the small
. Of course this effect is reasonably negligible in the case of a black body cavity, owing to the small ![]() related to the usual cavity temperature and its fluctuations. Yet the following examples aim to show that
related to the usual cavity temperature and its fluctuations. Yet the following examples aim to show that ![]() is conceptually significant in principle, even though
is conceptually significant in principle, even though![]() . If such a mass fluctuation is indeed allowed to occur, then it is significant to investigate the behavior of the transient formation of
. If such a mass fluctuation is indeed allowed to occur, then it is significant to investigate the behavior of the transient formation of ![]() and
and ![]() related to
related to![]() . Expectedly, this brings to the classical Kepler problem, where either mass orbits in the gravity field of the other; so, let us regard for example
. Expectedly, this brings to the classical Kepler problem, where either mass orbits in the gravity field of the other; so, let us regard for example ![]() and
and![]() , where the subscripts stand for orbiting and gravity field. It is known that the general relativity predicts in this respect two effects, the perihelion precession of
, where the subscripts stand for orbiting and gravity field. It is known that the general relativity predicts in this respect two effects, the perihelion precession of ![]() around
around ![]() and the emission of gravitational waves. Since these effects are concomitant, being both features of any orbiting system, the following discussion aims to examine jointly both of them.
and the emission of gravitational waves. Since these effects are concomitant, being both features of any orbiting system, the following discussion aims to examine jointly both of them.
Consider first just Equation (19) used to calculate the quantum fluctuations and note that the ratio at right hand side can be rewritten defining k such that![]() : i.e., likewise as done to infer Equations (12) and (59), the definition of Planck force is again implemented here to introduce G into the present problem. So, thanks to the arbitrary numerical factor k, the energy
: i.e., likewise as done to infer Equations (12) and (59), the definition of Planck force is again implemented here to introduce G into the present problem. So, thanks to the arbitrary numerical factor k, the energy ![]() is rewritten in order to introduce the arbitrary displacement
is rewritten in order to introduce the arbitrary displacement ![]() too. Equation (19) reads thus
too. Equation (19) reads thus
![]() (63)
(63)
Introduce now at the right hand side the further mass![]() ; the last equation turns into
; the last equation turns into
![]()
This result becomes next more familiar via a formal and elementary manipulation. Eliminate ![]() introducing the modulus of classical angular momentum
introducing the modulus of classical angular momentum ![]() of
of![]() , being
, being ![]() the average orbital velocity of the mobile mass
the average orbital velocity of the mobile mass ![]() and w the num- erical coefficient taking into account the vector nature of M and
and w the num- erical coefficient taking into account the vector nature of M and![]() ; this allows con- sidering at the right hand side the modulus of
; this allows con- sidering at the right hand side the modulus of![]() . Eliminating thus
. Eliminating thus ![]() at the right hand side, the last formula reads
at the right hand side, the last formula reads
![]()
Eventually, recalling that ![]() according to the initial definition (3), this equation reads
according to the initial definition (3), this equation reads
![]()
At the left hand side, the energies appear through a numerical coefficient times a ratio of the respective fluctuations. Consider now the case where this factor is![]() . Of course, nothing requires just this condition, which however is in principle possible and deserves attention for the related consequence of the initial Equation (63): this particular case is interesting because the left hand side can be regarded as a square probability
. Of course, nothing requires just this condition, which however is in principle possible and deserves attention for the related consequence of the initial Equation (63): this particular case is interesting because the left hand side can be regarded as a square probability![]() . Hence, it is appropriate to identify
. Hence, it is appropriate to identify ![]() with the product of two probabilities, that of angular displacement
with the product of two probabilities, that of angular displacement ![]() and that concerning the related tangential velocity component of
and that concerning the related tangential velocity component of![]() ; clearly the velocity component of
; clearly the velocity component of ![]() corresponding just to the advancement direction
corresponding just to the advancement direction ![]() in any point along the orbit has probability 1/3, because the independent local components of
in any point along the orbit has probability 1/3, because the independent local components of ![]() are three. If so, then
are three. If so, then ![]() takes the meaning compatible with a known formula of the general relativity: indeed, regarding the right hand side of the last result in a probabilistic way as
takes the meaning compatible with a known formula of the general relativity: indeed, regarding the right hand side of the last result in a probabilistic way as
![]() (64)
(64)
one recognizes the well known formula of the perihelion precession. This identification needs however a detailed justification and explanation: helps to this purpose a further result related to the energy loss via gravitational waves, still implied by Equation (63).
It is known that an isolated orbiting system irradiates energy all around in the space; the energy loss causes the orbit shrinking closer and closer towards the central mass. The starting input to demonstrate this effect in the present context is still Equation (19), rewritten identically via Equation (35) as follows
![]() (65)
(65)
i.e. k, whatever its specific value might be, has been split into ![]() and
and ![]() suitable to obtain a new value of energy
suitable to obtain a new value of energy ![]() from the early
from the early![]() . This is in principle possible because the values of these latter are both arbitrary. The fact that
. This is in principle possible because the values of these latter are both arbitrary. The fact that![]() , in agreement with the position (10), suggests assuming
, in agreement with the position (10), suggests assuming ![]() in order that
in order that
![]()
moreover if![]() , being q arbitrary proportionality constant, then
, being q arbitrary proportionality constant, then
![]()
Hence the first Equation (65) reads
![]()
where the right hand side is constant. Integrating now both sides over the solid angle![]() , one finds
, one finds
![]()
The square energy at the right hand side is constant; since it consists of fundamental constants only, thanks to the position assumed for![]() , it is reasonable to put
, it is reasonable to put![]() , being
, being ![]() the Planck power. Moreover, if the space around the orbiting system is homogeneous and isotropic, so that the orbiting system irradiates energy uniformly to all directions, one finds
the Planck power. Moreover, if the space around the orbiting system is homogeneous and isotropic, so that the orbiting system irradiates energy uniformly to all directions, one finds
![]() (66)
(66)
At this point the quantum uncertainty is of valuable help; it requires that ![]() and the momentum component
and the momentum component ![]() fulfill the condition
fulfill the condition![]() . In the present case, introducing the reduced mass
. In the present case, introducing the reduced mass ![]() of the orbiting system, the resulting uncertainty equations read
of the orbiting system, the resulting uncertainty equations read
![]() (67)
(67)
Replacing in Equation (66) h from the second equation, one infers![]() , i.e.
, i.e.
![]() (68)
(68)
With the minus sign and![]() , this expression is nothing else but the well known Einstein result of orbit contraction contextual to the emission of gravitational waves: indeed
, this expression is nothing else but the well known Einstein result of orbit contraction contextual to the emission of gravitational waves: indeed ![]() approximates well the numerical value 64/5 of his original formula. This means that the possible time evolution of the orbiting system described by this energy equation is due to the integer n which can take different discrete values at various times; correspondingly, the orbiting system changes energy and orbital distance from the central mass as well simply according to n. This quantum behavior already found in [12] is not surprising, since the starting point of the present reasoning was the quantum law governing the energy fluctuations. The related energy change
approximates well the numerical value 64/5 of his original formula. This means that the possible time evolution of the orbiting system described by this energy equation is due to the integer n which can take different discrete values at various times; correspondingly, the orbiting system changes energy and orbital distance from the central mass as well simply according to n. This quantum behavior already found in [12] is not surprising, since the starting point of the present reasoning was the quantum law governing the energy fluctuations. The related energy change ![]() of the orbiting system is immediately calculated. It is enough to note in this respect that
of the orbiting system is immediately calculated. It is enough to note in this respect that
![]()
where F is force. Simply considering the elementary positions
![]()
one finds
![]() (69)
(69)
The second equation is well known in the elementary Kepler problem identifying ![]() with the major semi-axis of the elliptic orbit. This result shows that the orbit size is subjected to change, concurrently to its angular displacement previously introduced; indeed Equation (69) concerns in particular the perihelion distance. Once again appears the Einstein formula for
with the major semi-axis of the elliptic orbit. This result shows that the orbit size is subjected to change, concurrently to its angular displacement previously introduced; indeed Equation (69) concerns in particular the perihelion distance. Once again appears the Einstein formula for ![]() and without minus sign. The explanation of these two results and their connection with Equation (64) is really simple.
and without minus sign. The explanation of these two results and their connection with Equation (64) is really simple.
Here ![]() with
with ![]() represents the energy gap
represents the energy gap ![]() related to the jump of
related to the jump of ![]() between orbits where
between orbits where ![]() to
to![]() , or in general to any
, or in general to any![]() , during the time range
, during the time range![]() ; of course this latter is not a differential dt, physically meaningless, but a finite time change of
; of course this latter is not a differential dt, physically meaningless, but a finite time change of ![]() necessary for any physical process to occur. This quantum point of view leading to Equations (68) and (69) is coherent with Equation (19) leading to the fluctuation Equation (53). The quantum standpoint also explains the lack of explicit minus sign in both Equations (68) and (69). In the Einstein result the orbital motion progressively decays towards distances closer and closer around the central gravitational mass with gradual energy loss only; accordingly, any orbiting system is destined to merge soon or later its bodies into a unique celestial body. In the present model instead Equation (68) is the distance gap between two contiguous orbits allowed with
necessary for any physical process to occur. This quantum point of view leading to Equations (68) and (69) is coherent with Equation (19) leading to the fluctuation Equation (53). The quantum standpoint also explains the lack of explicit minus sign in both Equations (68) and (69). In the Einstein result the orbital motion progressively decays towards distances closer and closer around the central gravitational mass with gradual energy loss only; accordingly, any orbiting system is destined to merge soon or later its bodies into a unique celestial body. In the present model instead Equation (68) is the distance gap between two contiguous orbits allowed with![]() , i.e.
, i.e. ![]() can in principle decay or be excited towards a lower or higher n-th orbits. This also means that two gravitational systems can even exchange “resonant” energy, e.g. by exchanging gravitons, likewise as two atoms of the same kind do by exchanging photons if either of them is in any electron excited state and the other in the fundamental state. It is also evident the analogy with the electrons that do not fall on the nucleus, but occupy stable quantum levels. So the lack of minus sign means that the formulas concern the amount of quantum energy exchanged regardless of whether this energy is released or absorbed by a given orbital system.
can in principle decay or be excited towards a lower or higher n-th orbits. This also means that two gravitational systems can even exchange “resonant” energy, e.g. by exchanging gravitons, likewise as two atoms of the same kind do by exchanging photons if either of them is in any electron excited state and the other in the fundamental state. It is also evident the analogy with the electrons that do not fall on the nucleus, but occupy stable quantum levels. So the lack of minus sign means that the formulas concern the amount of quantum energy exchanged regardless of whether this energy is released or absorbed by a given orbital system.
Consider now any point of the ellipse at a given time ![]() and at later time
and at later time![]() ; e.g. this point could be, but not necessarily must be, the perihelion. Equation (68) of
; e.g. this point could be, but not necessarily must be, the perihelion. Equation (68) of ![]() shows that this point moves radially from its initial position, as it is evident in the momentum/position uncertainty Equation (67) implementing radial conjugate dynamical variables. Equation (64) accounts instead for the tangential motion of
shows that this point moves radially from its initial position, as it is evident in the momentum/position uncertainty Equation (67) implementing radial conjugate dynamical variables. Equation (64) accounts instead for the tangential motion of ![]() in any given point along to the orbit: of course nothing, apart from the algebraic elaboration of the formulas, compels tangential displacement only or radial displacement only of the orbit of
in any given point along to the orbit: of course nothing, apart from the algebraic elaboration of the formulas, compels tangential displacement only or radial displacement only of the orbit of![]() . So, as previously emphasized, Equation (64) on the one hand and Equations (68) and (69) on the other hand simply complete each other in describing the dynamics of a unique phenomenon, i.e. the radial and tangential displacements of
. So, as previously emphasized, Equation (64) on the one hand and Equations (68) and (69) on the other hand simply complete each other in describing the dynamics of a unique phenomenon, i.e. the radial and tangential displacements of ![]() along its orbit that rotates and deforms as a function of time; this is coherent with the fundamental idea of deformation of the space time in the presence of a gravitational mass
along its orbit that rotates and deforms as a function of time; this is coherent with the fundamental idea of deformation of the space time in the presence of a gravitational mass![]() . This is in effect the physical meaning of
. This is in effect the physical meaning of ![]() in Equation (56), being
in Equation (56), being ![]() linked to
linked to ![]() via Equations (2) and (4). Note that
via Equations (2) and (4). Note that ![]() and
and ![]() can be exchanged while leaving identical the results: as nothing distinguishes the specific role of either of them from a physical point of view, one concludes that the concepts of gravitational and inertial mass are physically indistinguishable.
can be exchanged while leaving identical the results: as nothing distinguishes the specific role of either of them from a physical point of view, one concludes that the concepts of gravitational and inertial mass are physically indistinguishable.
The idea of introducing Planck units is fruitful and general, as it is confirmed also in the following reasoning.
Rewrite ![]() as
as
![]()
thanks to Equation (3). So, owing to Equation (21), Equations (19) and (15) yield
![]()
while being owing to Equation (21)
![]()
whence
![]() (70)
(70)
Since ![]() has physical dimensions of an energy, it is possible to put
has physical dimensions of an energy, it is possible to put
![]()
where ![]() is the Planck force; being
is the Planck force; being ![]() and
and ![]() arbitrary lengths, the energy at the left hand side can be certainly expressed as
arbitrary lengths, the energy at the left hand side can be certainly expressed as ![]() and in turn this latter as
and in turn this latter as![]() . These positions merely implement the general definitions of force and energy. The reason of having introduced the factor 1/2 appears soon after replacing in Equation (70); one finds
. These positions merely implement the general definitions of force and energy. The reason of having introduced the factor 1/2 appears soon after replacing in Equation (70); one finds
![]()
Note that ![]() for
for ![]() and for
and for![]() , i.e. in the absence of gravity field; also, owing to Equation (12),
, i.e. in the absence of gravity field; also, owing to Equation (12), ![]() implies
implies![]() . Just this is the reason of having introduced the factor 1/2: to describe the red shift of a photon moving away from a gravitational mass, the photon must be outside the boundary of its confinement radius (12) of m; i.e., the previous limits hold outside the “event horizon” of m, otherwise the photon could not freely escape to infinity. In conclusion the last equation reads
. Just this is the reason of having introduced the factor 1/2: to describe the red shift of a photon moving away from a gravitational mass, the photon must be outside the boundary of its confinement radius (12) of m; i.e., the previous limits hold outside the “event horizon” of m, otherwise the photon could not freely escape to infinity. In conclusion the last equation reads
![]()
Is really significant the fact that also this result of the general relativity is obtained implementing Equations (19) and (18), from which have been obtained Equation (50) and then the black body fluctuation Equation (53). A wider landscape of results of the general relativity is inferred via an “ab initio” theoretical model in [7] .
On the one hand, the result (60) highlights the quantum origin of the gravity force, simply inferable admitting time dependence of De Broglie momentum wavelength. In this respect Equation (59) prospects an interesting consequence as it yields
![]() (71)
(71)
So, owing to Equation (58), Equation (71) reduces to the trivial identity of two reciprocal surfaces A admitting the equality![]() ; this equality is reasonable, being mere consequence of the definitions of fine structure constant and Planck mass. Nonetheless, being
; this equality is reasonable, being mere consequence of the definitions of fine structure constant and Planck mass. Nonetheless, being ![]() and
and ![]() in the cgs system where
in the cgs system where![]() , one finds
, one finds
![]() (72)
(72)
The fact that both ratios are almost exactly equal to 1 is not trivial: in general one would expect simply![]() , with const equal to a generic numerical value; the fact that
, with const equal to a generic numerical value; the fact that ![]() shows that G and e are linked directly, not via a proportionality constant whose physical meaning should be specifically explained. Equation (72) reveals thus the direct correlation between e and G via
shows that G and e are linked directly, not via a proportionality constant whose physical meaning should be specifically explained. Equation (72) reveals thus the direct correlation between e and G via![]() , i.e. between gravitational and electromagnetic interaction.
, i.e. between gravitational and electromagnetic interaction.
On the other hand, despite the simplicity of approach, the compliance of the present model with the relativity, already emphasized by the corollaries of the Section 4, does not appear accidental. This point is elucidated next by four relevant examples.
1) According to Equation (2)![]() , whence
, whence ![]() with the arbitrary length
with the arbitrary length ![]() for
for![]() . Hence in analogy with Equation (1)
. Hence in analogy with Equation (1)![]() , being
, being![]() . Also, it is possible to write
. Also, it is possible to write
![]()
By dimensional reasons, it is also possible to put![]() , being
, being ![]() an arbitrary length. So, let us show that are definable two invariant equations linked by a square interval of size
an arbitrary length. So, let us show that are definable two invariant equations linked by a square interval of size![]() : from
: from
![]()
one expects both
![]()
as in effect it is true. Indeed it is possible to express ![]() as
as![]() , with q arbitrary constant; this result reads
, with q arbitrary constant; this result reads![]() . On the one hand, the right hand sides defines
. On the one hand, the right hand sides defines ![]() in the same reference system of
in the same reference system of![]() , i.e. it trivially concerns a smaller range. On the other hand, however,
, i.e. it trivially concerns a smaller range. On the other hand, however, ![]() is not necessarily related to
is not necessarily related to ![]() via the proportionality constant
via the proportionality constant ![]() only; being arbitrary by definition, it can be regarded in general as any
only; being arbitrary by definition, it can be regarded in general as any![]() , i.e.
, i.e. ![]() in another reference system mowing with respect to that of
in another reference system mowing with respect to that of![]() . Hence, the left hand side is an invariant; it also holds therefore for
. Hence, the left hand side is an invariant; it also holds therefore for![]() . Recalling Equation (9), the time and space invariants with
. Recalling Equation (9), the time and space invariants with ![]() read thus
read thus
![]() (73)
(73)
2) Let ![]() be the average velocity component with which one massive particle moves in the range
be the average velocity component with which one massive particle moves in the range ![]() and let the particle energy be subjected to fluctuations, during which its velocity component changes to the value
and let the particle energy be subjected to fluctuations, during which its velocity component changes to the value![]() . Assume therefore that the particle can move in
. Assume therefore that the particle can move in ![]() at average rates
at average rates ![]() or
or![]() , both arbitrary and allowed to occur during the time range
, both arbitrary and allowed to occur during the time range ![]() of Equation (2) because of an unforeseeable fluctuation; the only constrain is that, according to Equation (1),
of Equation (2) because of an unforeseeable fluctuation; the only constrain is that, according to Equation (1), ![]() requires
requires ![]() and
and![]() . Define therefore
. Define therefore
![]()
the notations emphasize the probabilities Π1 and Π2 that m, delocalized within![]() , travels just with either velocity before and after the fluctuation. Moreover,
, travels just with either velocity before and after the fluctuation. Moreover, ![]() emphasizes that anyway the particle moves, i.e. both velocity components are allowed to the particle; this is another way to state that fluctuation in fact occurred. But of course Π is effectively definable provided that
emphasizes that anyway the particle moves, i.e. both velocity components are allowed to the particle; this is another way to state that fluctuation in fact occurred. But of course Π is effectively definable provided that ![]() too, which allows regarding Π as pertinent probability that both Π1 and Π2 are possible for the particle in
too, which allows regarding Π as pertinent probability that both Π1 and Π2 are possible for the particle in![]() . This is the first boundary condition of the present problem. Since this reasoning in R must hold likewise in any other reference system
. This is the first boundary condition of the present problem. Since this reasoning in R must hold likewise in any other reference system![]() , it is possible to describe the situation for the range size
, it is possible to describe the situation for the range size![]() , i.e.
, i.e.
![]() (74)
(74)
where again q is an arbitrary constant. Let the primed and unprimed velocity components be defined in R' and R thinking that in general ![]() shifts with arbitrary rate with respect to
shifts with arbitrary rate with respect to![]() . Of course still holds in R' the boundary condition
. Of course still holds in R' the boundary condition ![]() in order that the energy fluctuation be regarded in an analogous way in both reference systems. This is the second boundary condition of the problem. Clearly the factor q > 0 represents the link between primed and unprimed quantities, i.e. it determines the transformation law of velocity components in R and
in order that the energy fluctuation be regarded in an analogous way in both reference systems. This is the second boundary condition of the problem. Clearly the factor q > 0 represents the link between primed and unprimed quantities, i.e. it determines the transformation law of velocity components in R and![]() : in fact the form (74) ensures that if
: in fact the form (74) ensures that if![]() , then anyway
, then anyway ![]() as well. In principle the boundary conditions are unsatisfied simply summing
as well. In principle the boundary conditions are unsatisfied simply summing ![]() and
and![]() , i.e. calculating
, i.e. calculating![]() ; yet the actual form of the sum of velocity components depends on the choice of q. Note in this respect that it is reasonable to put
; yet the actual form of the sum of velocity components depends on the choice of q. Note in this respect that it is reasonable to put
![]()
this position ensures that both ![]() and
and![]() , whatever they might be before and after the energy fluctuation, are in fact allowed in R and
, whatever they might be before and after the energy fluctuation, are in fact allowed in R and![]() . In other words, the positions just introduced regard the ratios
. In other words, the positions just introduced regard the ratios ![]() and
and ![]() as probabilities of states with and without fluctuation accessible to the particle, and thus in fact occurring, regardless of the choice of reference system. The first Equation (74) reads therefore
as probabilities of states with and without fluctuation accessible to the particle, and thus in fact occurring, regardless of the choice of reference system. The first Equation (74) reads therefore
![]()
so that
![]()
In this way ![]() is always consistent with the probabilistic meaning of
is always consistent with the probabilistic meaning of![]() .
.
This is the well known composition rule of the velocity components along the direction of motion of two reference system reciprocally displacing. The probabilistic meaning of a relevant relativistic property also appears here, already emphasized in demonstrating the perihelion precession [7] . This explains why even the relativistic result is compatible with the quantum approach.
3) It is easy at this point to highlight further the physical meaning of the length![]() . Consider the first Equation (11) and calculate the photon energy
. Consider the first Equation (11) and calculate the photon energy ![]() putting once more
putting once more![]() , in strict analogy with the first Equation (3); so, in par- ticular,
, in strict analogy with the first Equation (3); so, in par- ticular, ![]() too. The left hand side introduces the idea of frequency
too. The left hand side introduces the idea of frequency ![]() of a photon necessarily confined within a range
of a photon necessarily confined within a range ![]() via the position
via the position![]() ; this implies indeed a steady wavelength actually consisting of two half-wavelengths spreading at rate c throughout
; this implies indeed a steady wavelength actually consisting of two half-wavelengths spreading at rate c throughout![]() . Of course, Equation (3) holds also for the particular photon frequency
. Of course, Equation (3) holds also for the particular photon frequency ![]() related to such wavelength. Replacing once more h via the Planck length,
related to such wavelength. Replacing once more h via the Planck length, ![]() one finds
one finds
![]()
then, dividing both sides of ![]() by
by![]() , the result is
, the result is
![]()
Hence, ![]() of Equation (12) appears again here through the length
of Equation (12) appears again here through the length![]() . The circular frequency
. The circular frequency ![]() shows that the photon cannot escape from the gravitational field of m, the photon can only “orbit” around m at the black hole distance
shows that the photon cannot escape from the gravitational field of m, the photon can only “orbit” around m at the black hole distance ![]() from the center of gravity. Obviously, this conclusion could be inferred for the second Equation (11) too. The interest to quote here a result already found is that of rising an interesting question: what happens if the photon transits a a distance
from the center of gravity. Obviously, this conclusion could be inferred for the second Equation (11) too. The interest to quote here a result already found is that of rising an interesting question: what happens if the photon transits a a distance ![]() from m greater than that compelling its confinement? The most intuitive answer is that the photon should be simply deviated from its asymptotic straight propagation because of the presence of gravity field of m, which reasonably deforms the surrounding space time. Let be therefore according to Equation (12)
from m greater than that compelling its confinement? The most intuitive answer is that the photon should be simply deviated from its asymptotic straight propagation because of the presence of gravity field of m, which reasonably deforms the surrounding space time. Let be therefore according to Equation (12)
![]() (75)
(75)
and write then identically
![]() (76)
(76)
Defining an angle ![]() via the arc
via the arc ![]() of circumference of radius
of circumference of radius ![]() such that
such that![]() , the left hand side becomes
, the left hand side becomes![]() . Implement once more a probabilistic approach, noting that
. Implement once more a probabilistic approach, noting that ![]() is compatible with
is compatible with![]() . Is in particular interesting the case where
. Is in particular interesting the case where![]() : indeed
: indeed ![]() can be defined for a photon coming from minus infinity, approaches m and proceeds towards infinity after being deviated by the gravitational field of m; however this case is physically indistinguishable from that where the photon comes from infinity and proceeds towards minus infinity after an identical deviation. In other words
can be defined for a photon coming from minus infinity, approaches m and proceeds towards infinity after being deviated by the gravitational field of m; however this case is physically indistinguishable from that where the photon comes from infinity and proceeds towards minus infinity after an identical deviation. In other words ![]() must be such that
must be such that![]() , whereas of course
, whereas of course![]() : i.e. the photons is anyway deviated wherever it comes from or proceeds to. Since however either chance only actually happens and has probability
: i.e. the photons is anyway deviated wherever it comes from or proceeds to. Since however either chance only actually happens and has probability![]() , the previous result reads
, the previous result reads
![]()
This is the well known formula of the light beam bending in a gravitational field, since the angle defining the arc of circumference is equal to that between the tangents to the circumference at the boundaries of the arc, which yield the sought path deviation.
4) Note eventually that ![]() defines an invariant interval
defines an invariant interval ![]() whatever
whatever ![]() and
and ![]() might be. Of course this invariance property of the range size
might be. Of course this invariance property of the range size ![]() holds even if one considers in particular according to Equation (73)
holds even if one considers in particular according to Equation (73)
![]()
as in this case both addends at the left hand side remain themselves identically unchanged in two different inertial reference systems in reciprocal constant motion. This expression does not consider the mass of a particle possibly present in the space time. Consider now Equation (75) and introduce an arbitrary distance![]() , i.e. outside the confinement range, and consider the gravity field of M at an arbitrary point outside its event horizon; then Equation (12) yields
, i.e. outside the confinement range, and consider the gravity field of M at an arbitrary point outside its event horizon; then Equation (12) yields
![]()
being ![]() the local velocity defined by
the local velocity defined by ![]() just at a distance
just at a distance![]() . Hence
. Hence
![]() (77)
(77)
Replacing ![]() with
with![]() , Equation (77) yields according to Equation (73)
, Equation (77) yields according to Equation (73)
![]()
Simple considerations show that the right hand side reduces to the form ![]() in spherical coordinates; this is thus nothing else but the metric of the general relativity formulated by Schwarzschild. However this last result shows a crucial difference from the Einstein metrics: the latter assumes that the boundary of the ranges therein appearing are exactly knowable as in the classical physics, the former are instead uncertainty ranges that by definition satisfy the Heisenberg principle [7] . On the one hand this formal analogy explains why the formulas of the general relativity are also found via quantum approach; on the other hand their conceptual difference from the classical physics explains the difficulty of bridging relativistic and quantum ideas. However, the present reasoning shows that the link between quantum and relativistic physics exists indeed and is easily identifiable with the help of elementary considerations. Just this remarkable circumstance allows bridging quantum physics and relativity, despite the Einstein space time metrics is essentially classical physics extraordinarily enriched by the key concepts of four-dimensionality and covariancy of physical laws. In lack of a radically alternative way to infer the relativistic formulas, the mere attempt of modifying or perturbing the standard formulation of the general relativity to bridge deterministic metrics and probabilistic character of the non-real and non-local quantum world, would be difficult or even self-contradicting.
in spherical coordinates; this is thus nothing else but the metric of the general relativity formulated by Schwarzschild. However this last result shows a crucial difference from the Einstein metrics: the latter assumes that the boundary of the ranges therein appearing are exactly knowable as in the classical physics, the former are instead uncertainty ranges that by definition satisfy the Heisenberg principle [7] . On the one hand this formal analogy explains why the formulas of the general relativity are also found via quantum approach; on the other hand their conceptual difference from the classical physics explains the difficulty of bridging relativistic and quantum ideas. However, the present reasoning shows that the link between quantum and relativistic physics exists indeed and is easily identifiable with the help of elementary considerations. Just this remarkable circumstance allows bridging quantum physics and relativity, despite the Einstein space time metrics is essentially classical physics extraordinarily enriched by the key concepts of four-dimensionality and covariancy of physical laws. In lack of a radically alternative way to infer the relativistic formulas, the mere attempt of modifying or perturbing the standard formulation of the general relativity to bridge deterministic metrics and probabilistic character of the non-real and non-local quantum world, would be difficult or even self-contradicting.
8. Conclusions
Starting from elementary considerations, the present model is allowed to describe the fluctuations in a wider theoretical context that includes even relativistic implications. No “ad hoc” hypothesis has been necessary to infer relativistic results, which deserve a few final remarks. The first one emphasizes that in the present context they have been obtained regardless of any preliminary consideration about the covariancy of the physical laws and even about the metrics describing the space time deformation in the presence of matter; actually, instead, the hidden probabilistic meaning of the most famous results of the general relativity is easily acknowledgeable. The second one stresses an open point left by Equation (56) and omitted for brevity taking the absolute value of F in Equation (60), i.e. that the space time deformation inherent the time dependence of ![]() could imply in principle contraction or expansion of the range
could imply in principle contraction or expansion of the range ![]() and thus both signs of
and thus both signs of![]() ; hence, the signs of F correspond not only to attractive or repulsive interaction of the charges
; hence, the signs of F correspond not only to attractive or repulsive interaction of the charges ![]() and
and![]() , well known, but also to different chances of gravity force. This point, also remarked in [7] [12] , opens a critical problem about the existence of the anti-gravity. This conclusion deserves detailed investigation, too long and complex to be exposed in a short conclusion.
, well known, but also to different chances of gravity force. This point, also remarked in [7] [12] , opens a critical problem about the existence of the anti-gravity. This conclusion deserves detailed investigation, too long and complex to be exposed in a short conclusion.
A final remark deserves attention. With little effort and elementary mathematical formalism, Einstein could anticipate himself as done here the most significant discoveries of his general relativity: i.e., as side corollaries of Equation (54) describing the black body fluctuation. Unfortunately his paper [10] , despite its great historical relevance, was too purposely focused on the new born Planck physics. May be, the reluctance of Einstein to accept the weird quantum ideas has been the main conceptual obstacle to his opening towards the possible implications of the quantum fluctuations. It is surprising that great intuitions like the photon and the far reaching model of specific heat of solids settled eventually with the mere “hidden variables” of the EPR paradox. The present paper confirms indeed that there is no conceptual gap between quantum and relativistic ideas, as the conceptual foundations of both theories are actually rooted in the quantum concept of space time uncertainty [13] .
Cite this paper
Tosto, S. (2016) Black Body Quantum Fluctuations and Rela- tivity. Journal of Modern Physics, 7, 1668- 1701. http://dx.doi.org/10.4236/jmp.2016.713152
References
- 1. Siegel, R. and Howell, J.R. (2002) Thermal Radiation Heat Transfer. Volume 1, Taylor and Francis Ed., 7.
- 2. Adkins, C.J. (1983) Equilibrium Thermodynamics. Cambridge University Press, Cambridge, 50.
http://dx.doi.org/10.1017/CBO9781139167703.005
- 3. Carplus, R. and Neuman, M. (1953) Physical Review Letters, 83, 776.
http://dx.doi.org/10.1103/PhysRev.83.776
- 4. Bergmann, L., Schaefer, C. and Niedrig, H. (1999) Optics of Waves and Particles. W. de Gruyter Ed., Berlin, 595.
- 5. Irons, F.E. (2004) American Journal of Physics, 72, 1059.
http://dx.doi.org/10.1119/1.1767098
- 6. Varro, S. (2006) Einstein’s Fluctuation Formula. An Overview.
arxiv.org/pdf/quant-ph/0611023
- 7. Tosto, S. (2016) Journal of Advances in Physics, 6, 3408-3469.
- 8. Amelino-Camelia, G. (2002) Physics Letters B, 528, 181-187.
- 9. Dandliker, R. (2000) The Concept of Modes in Optics and Photonics. 6th International Conference on Education and Training in Optics and Photonics, 3831, 193-198.
- 10. Einstein, A. (1909) Physikalische Zeitschrift, 10, 185-193.
- 11. Landau, L. and Lifshits, E. (1966) Theorie du Champ (in French). Ed MIR, Moscow.
- 12. Tosto, S. (2013) Physics International, 4, 135-151.
http://dx.doi.org/10.3844/pisp.2013.135.151
- 13. Tosto, S. (2014) International Journal of Physics and Astronomy, 27, 1136.





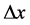 during a time range
during a time range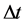 . It is in principle possible to express
. It is in principle possible to express 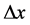 as a function of the Compton length
as a function of the Compton length 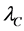 of the particle; so define the range size in
of the particle; so define the range size in 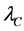 units putting
units putting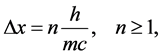 (1)
(1)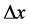 where the particle is allowed to move cannot be smaller than
where the particle is allowed to move cannot be smaller than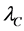 , which is an intrinsic physical property of the particle itself through its mass m.
, which is an intrinsic physical property of the particle itself through its mass m. , being v the component of velocity of the particle along
, being v the component of velocity of the particle along : is attracting the chance that
: is attracting the chance that 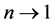 is consistent with
is consistent with 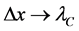 whereas
whereas 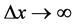 for
for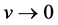 , in agreement with the arbitrary size of
, in agreement with the arbitrary size of 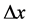 and value of v in a given reference system R. The formal choice of introducing the range size in
and value of v in a given reference system R. The formal choice of introducing the range size in 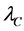 units does not exclude thinking even a photon confined in
units does not exclude thinking even a photon confined in 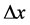 during a time range
during a time range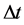 , which compels therefore defining
, which compels therefore defining















































































































































































































































































































































































































































































































































































































































































































































































































