Received 23 June 2016; accepted 19 August 2016; published 22 August 2016

ABSTRACT

Orthodox quantum mechanics is a highly successful theory despite its serious conceptual flaws. It renounces realism, implies a kind of action-at-a-distance and is incompatible with determinism. Orthodox quantum mechanics states that Schrödinger’s equation (a deterministic law) governs spontaneous processes while measurement processes are ruled by probability laws. It is well established that time dependent perturbation theory must be used for solving problems involving time. In order to account for spontaneous processes, this last theory makes use of laws valid only when measurements are performed. This incoherence seems absent from the literature.

Keywords:

Quantum Measurements―Time Dependent Perturbation Theory

1. Introduction

The first formulation of quantum mechanics is due to P. A. M. Dirac from 1930 [1] . J. von Neumann asserted that Dirac’s formalism could scarcely be surpassed in brevity and elegance, but it was deficient in mathematical rigor ( [2] , p. 7). A couple of years later von Neumann published his Mathematische Grundlagen der Quantenmechanik [3] . Many other versions of the theory followed these pioneer contributions, most of them motivated by the desire to solve the measurement problem. Von Neumann’s formulation continues, however, to be preferred to other approaches and, at present, it is frequently the only one taught at the academy. It is known as orthodox (ordinary or standard) quantum mechanics (OQM), although it is sometime referred to as the Copenhagen interpretation.

OQM refers to individual systems and consists of five axioms, two of them concerning measurements ( [2] , p. 5). One is a generalization of Born’s postulate and fixes the possible results of a measurement and their corresponding probabilities. The other is the projection postulate. It determines the final state to which the initial state collapses (is projected, is reduced, jumps) as a result of measurement.

Since the beginning OQM, and in particular its projection postulate, was the target of merciless criticism. Many and very conspicuous scientists denounced what they considered its flaws. For instance, A. Einstein pointed out that

1) There is a conflict between determinism and OQM. He stressed this issue frequently, as evidenced in his letters to M. Born of December 12, 1926, and of September 7, 1944 [4] .

2) OQM implies a kind of action-at-a-distance. In 1927, during the Fifth Solvay Congress, he showed that a peculiar kind of action-at-a-distance is inherent to the hypothesis that the state vector |yñ completely describes the state of an individual system (as established in OQM) ( [2] , p. 116) [5] [6] .

3) OQM introduces a subjective element into the theory through the projection postulate. This is an unacceptable procedure to account for processes happening in a world which objectively exists. Einstein insisted on this point repeatedly. For instance, referring to Maxwell’s influence on the evolution of the idea of physical reality he asserted: “The belief in an external world independent of the perceiving subject is the basis of all natural science” [7] .

In addition to these issues, OQM presents a conflict with conservation laws which has been largely ignored. We dealt with this subject some years ago and concluded that in the framework of OQM conservation laws are strictly valid in spontaneous processes (in fact they are theorems which can be derived from the axioms) but have only a statistical sense in measurement processes [8] - [12] .

Another source of problems is that OQM imposes two laws of change of the state vector |yñ [13] . Since it seems there is no way to reduce to one another, it would be desirable for OQM to unambiguously determine the precise conditions under which each of these laws would apply. Unfortunately this is not the case. J. S. Bell complains: “during ‘measurement’ the linear Schrödinger evolution is suspended and an ill-defined ‘wave- function collapse’ takes over. There is nothing in the mathematics to tell what is ‘system’ and what is ‘apparatus’, nothing to tell which natural processes have the special status of ‘measurements’. Discretion and good taste, born from experience, allows us to use quantum theory with marvelous success, despite the ambiguity of the concepts named above in quotation marks. But it seems clear that in a serious fundamental formulation such concepts must be excluded” ( [14] , p. 160).

The absence of a rule to determine which law must be applied is the worst flaw that OQM confronts [12] [15] .

2. Orthodox Quantum Mechanics: A Very Successful Theory

Quoting M. Jammer [2] , M. Bunge says that “there can be no doubt that quantum theory is a good approximation to the truth-which is not to say that it is perfect. Thousands upon thousands of observations and experiments have confirmed its predictions in an amazing range of fields, from particle and atomic physics to solid state physics and astrophysics, usually with an astounding accuracy” ( [16] , p. 167). While J. S. Bell emphatically asserts: “ORDINARY QUANTUM MECHANICS (as far as I know) IS JUST FINE FOR ALL PRACTICAL PURPOSES” (capital letters in the original) [17] .

M. Tegmar and J. A. Wheeler detail: “The Copenhagen interpretation [in the present paper named OQM] provided a strikingly successful recipe for doing calculations that accurately described the outcomes of experiments, but the suspicion lingered that some equation ought to describe when and how this collapse occurred. Many physicists took this lack of an equation to mean that something was intrinsically wrong with quantum mechanics and that it would soon be replaced by a more fundamental theory that would provide such an equation. So rather than dwell on ontological implications of the equations, most physicists forged ahead to work out their many exciting applications…” [18] .

They continue: “This pragmatic approach proved stunningly successful. Quantum mechanics was instrumental in predicting antimatter, understanding radioactivity (leading to nuclear power), accounting for the behavior of materials such as semiconductors, explaining superconductivity and describing interactions such as those between light and matter (leading to the invention of the laser) and of radio waves and nuclei (leading to magnetic resonance imaging). Many successes of quantum mechanics involve its extension, quantum field theory, which forms the foundations of elementary particle physics…” [18] .

At this point we should perhaps listen to R. P. Feynman declaring: “I can safely say that nobody understands quantum mechanics” [19] . So, even if everybody recognizes that quantum mechanics is fine for all practical purposes, nobody understands it. What strange a situation!

The majority of processes involved in the phenomena mentioned by Tegmar and Wheeler are not measurement but spontaneous processes. On the one hand, OQM ensures that the Schrödinger equation gives an account for them. On the other hand, most of these processes depend on time. According to Dirac, their analyses require the application of the method provided by time dependent perturbation theory (TDPT). In his words, “[this] method must… be used for solving all problems involving a consideration of time… or more generally problems in which the perturbation varies with the time in any way…” ( [1] , p. 168; emphases added). A similar idea is expressed by W. Heitler in his study of radiation problems ( [20] , p. 137-138).

In the next section we shall see that TDPT involves not only the Schrödinger equation (a deterministic law governing spontaneous processes) but also laws which are valid only when measurements are performed.

3. A Critical Review of Time Dependent Perturbation Theory

In the following we sketch the essential features of TDPT. For more details see for instance: D. R. Bes ( [21] , Chapter IX); C. Cohen-Tannoudji et al. ( [22] , Chapter XIII); P. A. M. Dirac ( [1] , Chapter VII); W. Heitler ( [20] , Chapter IV); E. Merzbacher ( [23] , Chapter XIX); and/or A. Messiah ( [24] , Chapitre XVII). Note: Symbols used by these authors may have been changed for homogeneity.

The aim of TDPT is to calculate the transition probability between stationary states (i.e. eigenstates of a Hamiltonian E which does not depend explicitly on time) induced by a time dependent perturbation W(t). The theory deals with processes having two clearly different stages. The first governed by the Schrödinger equation. The second ruled by probability laws. According to OQM formalism, Schrödinger equation governs spontaneous processes; Born’s postulate and/or the projection postulate apply only when measurements are performed. The fact that TDPT requires the application of postulates concerning measurements to give an account for processes supposedly spontaneous is at the very heart of OQM incoherence.

Let us work out separately the two stages mentioned. We start with a physical system with Hamiltonian E, called the non-perturbed Hamiltonian. Its eigenvalue equations are

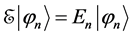(1)

where E_n (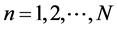) are the eigenvalues of E and |j_nñ the corresponding eigenvectors. For the sake of simplicity we shall consider E spectrum to be entirely discrete and non-degenerate. All the E_n and |j_nñ are supposed to be known.

First stage: Let |ψ(t)ñ be the system’s state at time t. We assume that at the initial time t = 0, the system is in the stationary state |j_iñ, which is the eigenvector of the non-perturbed Hamiltonian E corresponding to the eigenvalue E_i. At this instant the time dependent perturbation W(t) is applied. So for t ³ 0 the total, perturbed Hamiltonian is

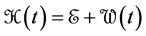(2)

As long as no measurements are performed, the process is spontaneous and ruled by the Schrödinger equation

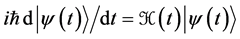(3)

where ħ is Planck’s constant divided by 2p and i is the imaginary unity. The solution |ψ(t)ñ of this equation which corresponds to the initial condition |ψ(0)ñ = |j_iñ is unique. This means that |ψ(t)ñ is completely determined by the initial state |ψ(0)ñ and the total Hamiltonian H(t), which includes the perturbation W(t). The state |ψ(t)ñ can be written

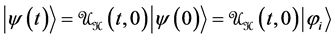(4)

where 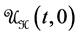is the evolution operator corresponding to the total Hamiltonian H(t) which acts during the time interval 0 ® t. To stress that |ψ(t)ñ depends on the initial state |j_iñ and on the total Hamiltonian H(t), or if preferred on the perturbation W(t), we write

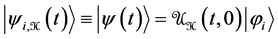(5)

Second stage: At t_f the system’s state is. Then, it is said, the probability the system has to be found in the state |j_fñ is.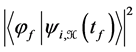

We sum up: In the first stage the system, initially in the stationary state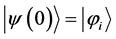, follows a Schrödinger evolution which leads it to the state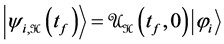; note that, in general, the state does not coincide with any stationary state |j_nñ (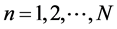). In the second stage the system jumps from 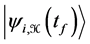to one of the stationary states |j_nñ. The whole process leads the system from the stationary state |j_iñ to the stationary |j_fñ (in particular it can result |j_fñ = |j_iñ).

The evolution during the first stage is an automatic change; at time t_f the system state cannot be different from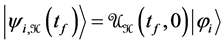. By contrast, the jump from to one of the stationary states |j_nñ is ruled by probability laws. The associated probability is by definition the transition probability between the initial stationary state |j_iñ and the final stationary state |j_fñ induced by the perturbation W(t) during the time interval 0 ® t_f and has the expression

(6)

In the following diagram we show the complete process leading the system from the initial |j_iñ to one of the possible final states |j_fñ.

Everything happens as if at time t_f a measurement of the non-perturbed energy, represented by the operator E, has been performed. According to Born’s postulate the possible results are the eigenvalues E_n ()

with probabilities given by. If the measurement yields the result E_f, the projection postulate

ensures that the system jumps from the state to the eigenstate |j_fñ.

Messiah expresses this idea in the following terms: “Supposons qu’à l’instant initial t = 0 le système se trouve dans l’un des états propres de E, l’état |j_iñ par exemple. Nous nous proposons de calculer la probabilité de le trouver à l’instant t_f dans un autre état propre de E, l’état |j_fñ par exemple, dans l’éventualité d’une mesure à cet instant. Soit cette quantité, c’est par définition la probabilité de transition de |j_iñ en |j_fñ” ( [24] , p. 621; emphases added).

Assuming that the initial state is |ψ(0)ñ = |j_iñ, Dirac asserts:“If there were no perturbation, i.e. if the Hamiltonian were E, [the state |ψ(t)ñ] would be stationary. The perturbation causes the state to change” ( [1] , p.

172). Supposing the deterministic law valid, the state results ( [1] , p. 109). Then,

he says: “is the probability of a transition taking place from state |j_iñ to state |j_fñ during the time interval 0 → t_f…” ( [1] , p. 172). Even though Dirac does not mention measurements, it is quite clear that he applies here a law valid only when measurements are performed.

Other authors proceed in a similar way. When introducing TDPT they do not mention measurements. Instead they make assertions such as: “Our objective is to calculate transition amplitudes between the relevant unperturbed eigenstates, owing to the presence of the perturbation…” ( [23] , p. 483); or “We want to study the transitions which can be induced by the perturbation…” ( [22] , p. 1285); or “The transition probability between the initial state |j_iñ and the final state |j_fñ is induced by the perturbation…” ( [21] , p. 142); etc.

There is a difference between Messiah’s and other authors’ statement of the problem worth mentioning. According to Messiah transitions to particular outcomes (either |j₁ñ, or |j₂ñ, or |j_Nñ) are the result of a measurement of the unperturbed Hamiltonian E. Other authors suggest that these transitions are not the result of a measurement of E, but of a perturbation of E. A perturbation of E is completely different from a measurement of E. When the perturbation W(t) is applied, the Hamiltonian changes from E to E + W(t), but the Schrödinger evolution is not suspended. By contrast, a measurement does suspend the Schrödinger evolution.

Paraphrasing Bell, even if nothing has been measured, discretion and good taste allow us to assume that a (virtual?) measurement of the physical quantity represented by the non-perturbed Hamiltonian E is performed at time t_f. “There is a long tradition of using the textbooks postulate of wave-function collapse as a pragmatic ‘shut up and calculate’ recipe” [18] . We have just shown how it works!

4. Conclusions

OQM marvelous success in the area of experimental predictions is mostly based on TDPT. It is agreed that the method provided by this last theory must be used for solving all problems involving a consideration of time, including spontaneous time dependent processes. This is, for instance, the case of absorption and emission of light and of processes occurring in semiconductors. To give an account for such spontaneous processes, however, TDPT requires the application of a law which is not valid in spontaneous processes. This is a flagrant incoherence we have not noticed in the literature.

Quantum weirdness has been traditionally associated with the measurement problem. To solve it, different authors have suggested several strategies. Among them are Statistical interpretation of quantum mechanics [25] , Many worlds interpretation [26] , Decoherence [18] and Continuous spontaneous localization theory [27] . We have addressed these and other proposed solutions of the measurement problem in previous papers [6] [9] [12] . Even if valuable, these contributions do not solve the measurement problem, let alone OQM incoherence pointed out in the present study.

We maintain that OQM weirdness is not limited to the measurement problem. It is much more serious and justifies a radical revision of the theory.

Acknowledgements

I am indebted to Professor J. C. Centeno for many fruitful discussions.

Cite this paper

M. E. Burgos, (2016) Success and Incoherence of Orthodox Quantum Mechanics. Journal of Modern Physics,07,1449-1454. doi: 10.4236/jmp.2016.712132

References