Journal of Modern Physics
Vol.07 No.07(2016), Article ID:66057,19 pages
10.4236/jmp.2016.77067
The Case against Dark Matter and Modified Gravity: Flat Rotation Curves Are a Rigorous Requirement in Rotating Self-Gravitating Newtonian Gaseous Discs
Dimitris M. Christodoulou1, Demosthenes Kazanas2
1Department of Mathematical Sciences and Lowell Center for Space Science and Technology, University of Massachusetts Lowell, Lowell, MA, USA
2Laboratory for High-Energy Astrophysics, NASA Goddard Space Flight Center, Greenbelt, MD, USA

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 19 February 2016; accepted 25 April 2016; published 28 April 2016
ABSTRACT
By solving analytically the various types of Lane-Emden equations with rotation, we have discovered two new coupled fundamental properties of rotating, self-gravitating, gaseous discs in equilibrium: isothermal discs must, on average, exhibit strict power-law density profiles in radius x on their equatorial planes of the form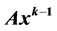 , where A and
, where A and 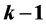 are the integration constants; and “flat” rotation curves precisely such as those observed in spiral galaxy discs. Polytropic discs must, on average, exhibit strict density profiles of the form
are the integration constants; and “flat” rotation curves precisely such as those observed in spiral galaxy discs. Polytropic discs must, on average, exhibit strict density profiles of the form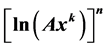 , where n is the polytropic index; and “flat” rotation curves described by square roots of upper incomplete gamma functions. By “on average”, we mean that, irrespective of the chosen boundary conditions, the actual profiles must oscillate around and remain close to the strict mean profiles of the analytic singular equilibrium solutions. We call such singular solutions the “intrinsic” solutions of the differential equations because they are demanded by the second-order equations themselves with no regard to the Cauchy problem. The results are directly applicable to gaseous galaxy discs that have long been known to be isothermal and to protoplanetary discs during the extended isothermal and adiabatic phases of their evolution. In galactic gas dynamics, they have the potential to resolve the dark matter―mod- ified gravity controversy in a sweeping manner, as they render both of these hypotheses unnecessary. In protoplanetary disc research, they provide observers with a powerful new probing tool, as they predict a clear and simple connection between the radial density profiles and the rotation curves of self-gravitating discs in their very early (pre-Class 0) phases of evolution.
, where n is the polytropic index; and “flat” rotation curves described by square roots of upper incomplete gamma functions. By “on average”, we mean that, irrespective of the chosen boundary conditions, the actual profiles must oscillate around and remain close to the strict mean profiles of the analytic singular equilibrium solutions. We call such singular solutions the “intrinsic” solutions of the differential equations because they are demanded by the second-order equations themselves with no regard to the Cauchy problem. The results are directly applicable to gaseous galaxy discs that have long been known to be isothermal and to protoplanetary discs during the extended isothermal and adiabatic phases of their evolution. In galactic gas dynamics, they have the potential to resolve the dark matter―mod- ified gravity controversy in a sweeping manner, as they render both of these hypotheses unnecessary. In protoplanetary disc research, they provide observers with a powerful new probing tool, as they predict a clear and simple connection between the radial density profiles and the rotation curves of self-gravitating discs in their very early (pre-Class 0) phases of evolution.
Keywords:
Dark Matter, Gravitation, Galaxies, Protoplanetary Discs

1. Introduction
A large number of observations, mostly in the 21 cm emission line of neutral hydrogen, have firmly established that the rotation curves of spiral galaxy discs do not exhibit a Keplerian falloff; in fact, most of them remain flat or slightly increasing as far away from the centers as they can be observed [1] - [22] . The radial scales over which the neutral hydrogen discs can be observed reach out to ~100 kpc in the largest spiral galaxies and since the rotation curves remain flat, it was postulated by many researchers that some unseen extended mass distribution ought to exist all the way out to hundreds of kiloparsecs from the galaxy centers. Thus the Dark Matter Hypothesis was born, and soon the news leaked out to the rest of the physics community and intensive and extensive searches for dark matter particles and fields boomed into existence. On the other hand, some researchers who certainly felt uncomfortable with this new “aetherial” hypothesis proposed that Newtonian gravity should instead be modified at galactic scales and beyond, in order to solve the problem of the fast rotation of HI galaxy discs [23] - [33] .
The gas in spiral galaxies is distributed in centrally concentrated, vertically thin discs. For this reason, it was expected that the rotation curves had to turn over at some intermediate radius and begin a decline that would be indicative of the absence of substantial amounts of matter at large radii. This view about the luminous matter is nowadays considered so settled and clear that it has made its way into introductory Astronomy textbooks that compare and contrast the kinematics of spiral galaxies to the kinematics observed in our solar system (the Keplerian falloff mentioned above). In this work, we show that this elementary perception is quite naive and totally wrong because it ignores the influence (in fact, the dominance) of pressure and enthalpy gradients in self- gravitating gaseous discs. Personally, we believe that it amounts to a blunder because, before the results described below and even back in the 1980s when all this was unfolding, we had important clues that pointed out the importance of gas pressure in determining the equilibrium structures of gaseous discs. For instance, the sound-crossing time at 10 kpc in a 104 K cold galaxy disc is 1 Gyr, a value that lies to within 1.5 - 3 of the rotation timescales at 10 kpc in all galaxies with rotation speeds of 100 - 200 km∙s−1. Gallagher et al. [34] noted that the star formation histories of a sample of irregular and spiral galaxies did not indicate the presence of dark matter in the low-mass galaxies of the sample. But the most obvious clue was the existence of the Mestel disc [35] , a centrally concentrated potential-density pair with a flat rotation curve (see also [36] ). The Mestel disc has always been considered just a toy model [37] and the situation did not improve when Schulz [38] showed that the finite Mestel disc requires significantly less mass to produce the flat rotation curve. The main argument against the universal adoption of the Mestel disc has been the absence of a physical law or reason that would make galaxy discs assume this specific surface density profile and rotation law.
The above argument is not based on solid reasoning. When nature shows us that she has widely adopted a specific property (the flat rotation curves in galaxy discs), Aristotelian Logic dictates that we should search for a new law or reason, in order to understand the universality of this property and establish its physical meaning; not to create ghosts (particles and fields), aethers, and new forces that effectively facilitate our aversion to con- fronting the facts.
We do not claim that the Mestel disc [35] is the answer to establishing the universality of flat rotation curves in galaxy discs; only that it has always been a telling clue that gravity does not pull the strings and is not in control in gaseous self-gravitating discs. Furthermore, we have solved the full Newtonian problem and we now know precisely how such universal rotation curves emerge in spiral galaxy discs. The resolution of this ubiquitous problem is the subject of this paper. Before we can delve into the physics of the problem, we need to correct some common misconceptions that appear in the theory of second-order differential equations and which also have made their way into the textbooks. We do so in Section 2. Then, in Section 3, we revisit the theory of rotating Newtonian isothermal gaseous-disc equilibrium models and we calculate analytically the mean shapes of their density profiles and their rotation curves. The results match precisely the shapes of the rotation curves of spiral galaxy discs with no additional assumptions of any kind. So these results make a strong case against both dark matter and modified gravity and their implications have far-reaching consequences all the way to cos- mology. For completeness, we describe in Section 4 polytropic models that also demand monotonically increas- ing rotation curves because they are subject to the same physical principles. These models are also applicable to very young protoplanetary discs (certainly to pre-Class 0 discs and possibly to the youngest Class 0 non- Keplerian discs). Finally, we conclude with a discussion of all the pertinent issues and our results in Section 5.
2. Second-Order Differential Equations and the Cauchy Problem
In mathematical physics, the trivial solutions of the various second-order differential equations are commonly ignored as being uninteresting; and too much attention is paid to the Cauchy problem in determining arbitrary constants as opposed to the internal properties of the equations themselves that have no regard for externally im- posed conditions of any type. Both of these practices are damaging as they work to hinder our efforts toward solving the physical problems described by the differential equations in the first place. Such practices are rele- vant to all linear and nonlinear second-order equations of physics, so we can discuss and clarify the various issues involved by using any well-known equation. We choose to make use of the Bessel differential equation in this section.
The Bessel equation [39]
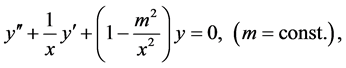 (1)
(1)
has regular solutions that are called Bessel functions of order m and a trivial solution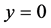 . The trivial solution is not singular as it can be obtained from the regular solutions by an appropriate choice of the arbitrary constants. Nevertheless, its name indicates that y = 0 is of no interest at all. It is also well-known that the Bessel functions all oscillate about the x-axis [39] , but this statement is grossly inaccurate and obscures the truth: the regular solutions oscillate about the trivial solution which just happens to coincide with the x-axis in this case. We demonstrate this important point by solving numerically an inhomogeneous
. The trivial solution is not singular as it can be obtained from the regular solutions by an appropriate choice of the arbitrary constants. Nevertheless, its name indicates that y = 0 is of no interest at all. It is also well-known that the Bessel functions all oscillate about the x-axis [39] , but this statement is grossly inaccurate and obscures the truth: the regular solutions oscillate about the trivial solution which just happens to coincide with the x-axis in this case. We demonstrate this important point by solving numerically an inhomogeneous 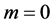 Bessel equation of the form
Bessel equation of the form
 (2)
(2)
along with nonsingular boundary conditions that attempt to initially push the regular solutions away from the new trivial solutions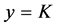 :
: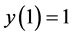 ,
, 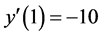 for K = 5; and
for K = 5; and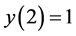 ,
, 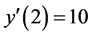 for
for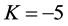 . The results are shown in Figure 1. Both regular solutions have nothing to do with the x-axis; instead, they turn around and settle into oscillations that clearly occur about the new trivial solutions
. The results are shown in Figure 1. Both regular solutions have nothing to do with the x-axis; instead, they turn around and settle into oscillations that clearly occur about the new trivial solutions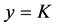 . This behaviour can be demonstrated for all linear second-order equations of mathematical physics with oscillatory regular solutions [40] and for (non)linear equations of the Lane-Emden type [41] - [45] . The lesson to be learned is that the so- called trivial solutions of second-order equations are not at all trivial. They are in fact favoured by the diffe- rential equations themselves which have no regard for the externally imposed boundary conditions. Thus, we will heretofore call these solutions the intrinsic solutions that are preferred and demanded by the equations themselves, irrespective of the externally imposed Cauchy problem.
. This behaviour can be demonstrated for all linear second-order equations of mathematical physics with oscillatory regular solutions [40] and for (non)linear equations of the Lane-Emden type [41] - [45] . The lesson to be learned is that the so- called trivial solutions of second-order equations are not at all trivial. They are in fact favoured by the diffe- rential equations themselves which have no regard for the externally imposed boundary conditions. Thus, we will heretofore call these solutions the intrinsic solutions that are preferred and demanded by the equations themselves, irrespective of the externally imposed Cauchy problem.
When the Cauchy problem is solved, as in Figure 1, the externally imposed boundary conditions are usually at odds with the underlying equation and the regular solutions cannot match the favoured intrinsic solution. As a result, the regular solutions are forced by the equation itself to oscillate about the intrinsic solution as soon as they intersect this favoured solution the first time. Thus, the intrinsic solutions act as attractors of the regular solutions which, in turn, are forced to always stay near and around the more dominant intrinsic solutions. We view this behaviour as a triumph of the differential equation (and its intrinsically favoured solution) over the Cauchy problem (and the particular solution it strives to produce).
This striking behaviour remains intact in at least some nonlinear second-order equations. Very clear examples in which rotation is involved can be found in [43] and [44] . Here we provide two additional nonlinear examples of the dominance of intrinsic solutions over regular solutions drawn from Lane-Emden equations [46] [47] in the absence of rotation. The isothermal Lane-Emden equations, take the form
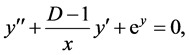 (3)
(3)
Figure 1. Numerical solutions of the m = 0 inhomogeneous Bessel differential Equation (2) subject to the following boundary conditions: in the 






where D is the dimensionality of space (


In stark contrast, the polytropic Lane-Emden equations, take the form

where n > 0 is the polytropic index, and it possesses the intrinsic solution y = 0. Although few analytic solutions are known [50] [52] , numerical integrations show that, depending on n, this equation has both oscillatory and nonoscillatory solutions. For Equation (4), we have derived a precise criterion for the existence of oscillatory solutions [45] . This criterion predicts that for D = 2 (cylindrical form), all solutions with odd integer n-values are oscillatory; while for D = 3 (spherical form), only the 




3. Isothermal Self-Gravitating Newtonian Gaseous Discs
In what follows, we use the arbitrary scaling constants 









The cylindrical isothermal Lane-Emden equation [46] [47] with rotation can then be written in dimensionless form as

This equation describes the radial (x) equilibrium of a rotating, self-gravitating, gaseous disc or cylinder in which the gas obeys the isothermal equation of state
Hayashi et al. [53] and Schmitz [55] studied also the stability of such equilibria and found that, except for the very flattened discs and the nearly spherical configurations, the intermediate models are stable. The very flattened discs in [53] , in particular, were unstable to ring formation that causes their equatorial power-law density profiles to become oscillatory, in agreement with the numerical solutions of Equation (5) obtained in [44] .
Despite the exact analytic results of the researchers quoted above, an objection has been raised over the years concerning the validity of using cylindrical coordinates to study axisymmetric, vertically thin discs rather than just infinite cylinders; and this is also the major sticking point for the present work, so it needs to be addressed in detail. We defer the analysis of the Lane-Emden equations for vertically thin discs to an Appendix because it is much easier to follow the derivations after the intrinsic analytic solution has been obtained for cylinders as follows.
Christodoulou & Kazanas [44] described a procedure for obtaining the intrinsic solution of Equation (5): If we equate the last two terms:

then this is an intrinsic solution provided that the rest of the equation (the radial variation of the logarithmic gra- dient of the enthalpy) vanishes:

Equations (6) and (7) form a system in which 


and then we solve Equation (6) to determine the rotation curve of the intrinsic solution:

where

The solution contains 3 free parameters, the integration constants A, B, and k. Parameter B sets the vertical scale of the rotation curve




Figures 2-4 show the shapes of the rotation curves obtained from Equations (9) and (10) for various choices of the constants A and k. The results are scale-invariant (a property of power-law density profiles), so the radial
Figure 2. Rotation curves of the intrinsic solution of the isothermal Lane-Emden equation for


Figure 3. As in Figure 2, but for
scale is arbitrary. It is not surprising (see Section 3.1 below) that, in these Newtonian models, one sees most of the shapes of the “flat” rotation curves observed in spiral galaxies.
The only shapes missing from the figures are those of the few falling rotation curves shown in [18] . Appa- rently, in some compact galaxies, the above equilibrium profiles did not endure (the sound-crossing time at 30 kpc for 
Figure 4. As in Figure 2, but for
case since the intrinsic solutions are favoured by the equilibrium differential equation itself (see Section 2) in the absence of other external forces. In the two galaxies observed by Casertano & van Gorkom [18] , certain segments of the rotation curves are flat and that indicates to us that the radial self-gravitational equilibrium has fallen apart at some locations but not (yet) everywhere in these discs.
The above results can be summarized as follows: The derived density profiles are simple power laws in radius and the rotation curves are flat or slightly increasing at large radii (Equations (9) and (10)) irrespective of the value of the index k. Spiral galaxies have always been fitted with exponential density profiles, thus we do not know which values of k occur in nature. Galaxy profiles will have to be fitted again, but the payoff this time will be substantial: when k is determined from observations, the large-scale rotation curve (away from the center) will also be obtained independently from the velocity measurements. Thus, the observational results will be tested for consistency within the same data set in each case. This also holds true for protoplanetary discs in their early isothermal or adiabatic (see Section 4 below) phases; but first we need to find such purely self-gravitating discs in a pre-Class 0 YSO (Young Stellar Object) stage, and the 21 cm HI line in emission or absorption may give us a chance [56] .
3.1. Physical Interpretation
But how can such power-law density profiles produce and support flat or slowly increasing rotation curves? The problem has always been that the centrifugal force remains too high in the outer regions of the disc where New- tonian gravity weakens substantially. How do these equilibrium models get around this discrepancy? The answer to these questions was given in [44] and we repeat it here: The Lane-Emden Equation (5) is a second-order differential equation. As such, it respects but does not rely solely on force balance. (As will be readily seen in Equation (12) below, force balance is guaranteed by the way that the specific enthalpy of the gas is operating.) This second-order equation describes locally the detailed radial (


where 




In that case, how and why does the average intrinsic solution (Equations (8) and (9)) come into existence? The answer to these questions is even more illuminating: The intrinsic solution was derived above by imposing two separate conditions, that the centrifugal force should match the gravitational force (see Equation (6) and the last two terms in Equation (11)):

while, at the same time, the log-gradient of the enthalpy should retire from the competition by assuming a con- stant profile (see Equation (7) and the leading term in Equation (11)):

This occurs only for a power-law density profile (Equation (8)) and for a specific rotation profile (Equations (9) and (10)), and these profiles become internal properties characteristic of the equilibrium disc or cylinder. Stated more simply, up until now people believed that rotation was not related to the structure of the equilibrium disc and that they could adopt any arbitrary rotation profile for gaseous self-gravitating discs. We see now that this is not true, the radial density and rotation profiles are strongly coupled and uniquely determined through the intrinsic solution discussed above.
The only surprise in this narrative is the unique way that the differential equation finds to promote and estab- lish the above intrinsic solution: rather than trying to simultaneously balance the variations of the three poten- tials involved at every single radius (not possible because the corresponding timescales vary widely at different radii), the disc assumes gradually a logarithmic specific-enthalpy profile determined from the solution of Equ- ation (13):

So it is the thermodynamic potential 




We understand physically the preceding results in the following manner: Self-gravity is a long-range force (by Gauss’s law, the gravitational potential at radius x depends on the entire mass interior to x) and it cannot adjust its potential in the disc to effect local changes to the density distribution. In other words, the density is a source term in the Poisson equation that determines the gravitational potential, but not the other way around. In stark contrast, enthalpy is a local potential whose action depends only on the local behaviour of the pressure and the density of the disc. When 

By doing that, the enthalpy uses the density in order to modify the sourcing of both the gravitational potential (via the Poisson equation
It is important to keep in mind that the enthalpy wins the struggle because the two equations of the intrinsic equilibrium solution (Equations (6), (7) or Equations (12), (13)) and the Poisson equation (
3.2. Concluding Remarks
The above equations give us a new probe into gaseous astrophysical disc systems (Equations (6) and (7)). For spiral galaxy discs, this probe ought to routinely confirm the above-described density-rotation coupling, as the observations already exist. At the same time, we are full of anticipation about what we can learn from the very early phases of purely self-gravitating protoplanetary discs (before the central protostars form and dominate the dynamics) for which the rotation curves have not been measured with accuracy yet, but the radial density profiles in Class 0 YSOs have been obtained [57] [58] . Our prediction, of course, is that, if found, such early discs (preferably earlier than Class 0) will be observed to have “flat” rotation curves.3
4. Polytropic Self-Gravitating Newtonian Gaseous Discs
The cylindrical polytropic Lane-Emden equation [46] [47] with rotation can be written in dimensionless form as

where 






We repeat the procedure outlined in Section 3 in order to obtain the intrinsic solution of Equation (16): If we equate again the last two terms:

then this is an intrinsic solution provided that the rest of the equation (the radial variation of the logarithmic gradient of the enthalpy) vanishes:

Equations (17) and (18) form a system in which 


and then we solve Equation (17) to determine the rotation curve of the intrinsic solution:

where B is the integration constant, 





The solution contains 4 free parameters, the integration constants A, B, k, and the polytropic index n. Para- meter B can adjust the vertical scale of the rotation curve


Figures 5-8 show the shapes of the rotation curves obtained from Equation (20) for two polytropes with 





Figure 5. Rotation curves of the intrinsic solution of the 


Figure 6. As in Figure 5, but for
Figure 7. Rotation curves of the intrinsic solution of the n = 3 polytropic Lane-Emden equation for

Figure 8. As in Figure 7, but for
noted in the figure captions as well: 1) for fixed n, the curves rise more steeply for steeper values of the index

4.1. Physical Interpretation
The polytropic Lane-Emden equation with rotation and its intrinsic solution assume the exact same forms as in the isothermal case (Section 3.1) when the polytropic equation of state 

The fact that the thermodynamic potential 



Furthermore, as we have seen above, a flat rotation curve does not imply and does not need a linearly increas- ing mass distribution. Even if the underlying density profile is decreasing in radius (as the light does in spiral galaxy discs), a rising rotation curve is a requirement in the equilibrium solutions derived in this section and in Section 3 so long as more mass is added incrementally with increasing radius (this is simply a restatement of Gauss’s law). Therefore, one can assume a constant mass-to-light ratio and build a Newtonian self-gravitating galaxy disc model with a declining mass distribution that will still be required to have a rising rotation curve provided that the disc may be thin, but not razor-thin; that 
4.2. Concluding Remarks
The polytropic intrinsic solution (Equations (17) and (18)) gives us a new probe into nonisothermal astro- physical disc systems. In particular, protoplanetary discs undergo various early phases of adiabatic evolution (figure 2 in [65] ). We predict that, if found, such discs will be observed to have the same fundamental characteristics (Equations (19) and (20)) irrespective of the polytropic index n appropriate for each adiabatic phase. In fact, observations of the density profiles, fitted with Equation (19), may be able to determine, not only the profile constants k and A, but also the value of n, thereby deriving the equation of state of the gas in- dependently from theoretical models. The only problem is that we need to find such systems very early in their development (see footnote 3 above), and this is a difficult task [56] [57] [66] .
5. Discussion
In this paper, we have investigated the Lane-Emden equations with rotation that describe the equilibrium struc- tures of rotating, self-gravitating, gaseous discs and cylinders (Sections 3 and 4; see also the Appendix). We have obtained new analytic singular solutions that we call intrinsic solutions because they are dictated and favoured by the differential equations themselves with no regard to physical boundary conditions that are externally imposed and that shape up the regular solutions of the equations (the Cauchy problem). In Sections 2-4, we have effectively shown that second-order differential equations (both linear and nonlinear) are at odds with the Cauchy problem because the equations show a strong preference for their own intrinsic solutions that, for inhomogeneous equations of the Lane-Emden type, cannot be obtained by solving the boundary-value problem (hence they are singular). The regular Cauchy-type solutions are then attracted to and forced to oscillate about the intrinsic solutions, which means that they do their best to match those dominant solutions. This results in “regular” oscillatory density and rotation profiles whose averages are precisely the underlying intrinsic solu- tions [40] [44] [45] . In this sense, the differential equations succeed in imposing their preferences to the Cauchy problem. This, by itself, is an important conclusion that has ramifications beyond astrophysics for the theory of second-order differential equations of mathematical physics.
The intrinsic solutions are very much related to the so-called trivial solutions of differential equations [44] . We now understand that there are no trivial solutions; in fact such solutions of second-order equations are quite dominant (Section 2): in many cases of interest, knowing the trivial solution of an equation implies that we know the average behaviour of all the regular solutions that depend on various types of boundary conditions but, nevertheless, end up oscillating about the intrinsic solution, provided that the differential equation is a harmonic oscillator (as the ordinary Bessel equations in Section 2; the nonisothermal Lane-Emden equations without rotation in Section 2; and the Lane-Emden equations with rotation in Sections 3 and 4).
The mean density and rotation profiles that we have derived analytically in Sections 3 and 4 are dominated by natural logarithms and power laws. This is the implicit reason that Marr [67] has recently suceeded in matching the shapes of the rotation curves of a sample of 37 spiral galaxies by using the log-normal probability distri- bution (and no dark matter or modified gravity) to describe the density profiles in the equatorial planes of the discs. This surface density distribution (Equation (2) in [67] ) is equivalent to a variable power law of the form 


where 


Returning to the astrophysical context, the intrinsic solutions of the various types of the Lane-Emden equation with rotation have, for the first time, succeeded in explaining the flat rotation curves of spiral galaxy discs without the need of invoking dark matter or modified gravity. Flat rotation curves are a rigorous requirement of Newtonian gravity in gaseous self-gravitating astrophysical discs (Sections 3.1 and 4.1). The only fair way to describe the results of Sections 3 and 4 is that Sir Isaac Newton [68] is vindicated once again, and our searches for dark matter in the universe and our attempts to modify Newtonian gravity (references are listed in Section 1) have sadly amounted to just a “wild-goose chase”. In fact, since the flat rotation curves of spiral galaxies can now be explained at such a fundamental level, the massive observational results collected over the years must be considered as yet another test that Newtonian gravity has successfully passed on scales of ~10-100 kpc and at nonrelativistic velocities. This is an impressive achievement when compared to previous tests conducted on and limited to scales no larger than that of our solar system.
Our results render the Dark Matter Hypothesis unnecessary on galaxy scales. This removes the largest pillar of this hypothesis (flat rotation curves have remained to this day the “strongest piece of evidence” in favour of dark matter, but not any longer). But this “aetherial” hypothesis is not about to roll over and die without a fight. The next areas of confrontation will be larger than galaxy scales and cosmology. We are very much encouraged from a recent report of the absence of dark matter on larger than galaxy-disc scales: Magain & Chantry [69] analyzed 25 gravitational lenses and found that their mass determinations indicate the absence of extended dark matter haloes all the way out to distances comparable to the Einstein ring (the separation between lensed quasar images).
On the other hand, we do not anticipate any serious problems materializing in cosmology because we do not believe that there currently is any credible observational evidence in favour of dark matter or modified gravity on those largest scales. In fact, some results that argue against the necessity for dark matter on various scales have timidly begun to appear [70] - [76] . For these reasons, here is how we approach the issue of dark matter now: Christiaan Huygens presented his theory of elastic longitudinal light waves propagating in “aether” to the Paris Academy of Sciences in 1678 and published his views a few years later [77] . That year, the physics world entered a Dark Age that lasted nearly 200 years, until the genious of Michelson & Morley [78] finally showed that the universe is not filled with aether. It seems that we also live in another Dark Age, the “Dark Matter Dark Age”, that commenced in the 1970s when K. C. Freeman [1] and others [2] - [22] reported that the rotation curves of spiral galaxies were not falling with radius. By all accounts, the current Dark Age has lasted for nearly 50 years; and the sooner we get out of it, the better for our understanding of the large scales of the universe around us.
The analytic solutions that we have derived in this work should also find applications in the field of proto- planetary disc research (Sections 3.2 and 4.2), especially if very young, purely self-gravitating discs could be found in the future [56] . At present, only observations of Class 0 YSOs are widely available [57] [58] , but these systems are not young enough and do not have flat rotation curves; their protostars have formed and they are changing the dynamics and kinematics of the discs.4 We are encouraged however by the report of Tsitali et al. [66] who discovered a rising rotation curve in the inner 2000-8000 AU of the “first hydrostatic core” candidate Cha-MMS1.
Acknowledgements
We thank Joel Tohline for feedback and guidance over many years; and John Marr, Hsi-Wei Yen, and Earl Schulz for many fruitful discussions, especially those concerning the observations of astrophysical self-gravitat- ing discs.
Cite this paper
Dimitris M. Christodoulou,Demosthenes Kazanas, (2016) The Case against Dark Matter and Modified Gravity: Flat Rotation Curves Are a Rigorous Requirement in Rotating Self-Gravitating Newtonian Gaseous Discs. Journal of Modern Physics,07,680-698. doi: 10.4236/jmp.2016.77067
References
- 1. Freeman, K.C. (1970) Astrophysical Journal, 160, 811.
http://dx.doi.org/10.1086/150474 - 2. Rogstad, D.H. and Shostak, G.S. (1972) Astrophysical Journal, 176, 315.
http://dx.doi.org/10.1086/151636 - 3. Roberts, M.S. and Rots, A.H. (1973) Astronomy & Astrophysics, 26, 483-485.
- 4. Bosma, A. (1978) The Distribution and Kinematics of Neutral Hydrogen in Spiral Galaxies of Various Morphological Types. Ph.D. Thesis, University of Groningen, Groningen.
- 5. Rubin, V.C. (1980) Astrophysical Journal, 238, 808-817.
http://dx.doi.org/10.1086/158041 - 6. Rubin, V.C., Ford Jr., W.K. and Thonnard, N. (1980) Astrophysical Journal, 238, 471-487.
http://dx.doi.org/10.1086/158003 - 7. Bosma, A. (1981a) Astronomical Journal, 86, 1791.
http://dx.doi.org/10.1086/113062 - 8. Bosma, A. (1981b) Astronomical Journal, 86, 1825.
http://dx.doi.org/10.1086/113063 - 9. Rubin, V.C., Ford Jr., W.K., Thonnard, N. and Burstein, D. (1982) Astrophysical Journal, 261, 439-456.
http://dx.doi.org/10.1086/160355 - 10. Bahcall, J.N. and Casertano, S. (1985) Astrophysical Journal, 293, L7-L10.
http://dx.doi.org/10.1086/184480 - 11. van Albada, T.S., Sancisi, R., Petrou, M. and Tayler, R.J. (1986) Philosophical Transactions of the Royal Society A, 320, 447-464.
http://dx.doi.org/10.1098/rsta.1986.0128 - 12. Kent, S.M. (1987) The Astronomical Journal, 93, 816-832.
http://dx.doi.org/10.1086/114366 - 13. Begeman, K.G. (1987) HI Rotation Curves of Spiral Galaxies. PhD Thesis, University of Groningen, Groningen.
- 14. Persic, M. and Salucci, P. (1988) Monthly Notices of the Royal Astronomical Society, 234, 131-154.
http://dx.doi.org/10.1093/mnras/234.1.131 - 15. Begeman, K.G. (1989) Astronomy & Astrophysics, 223, 47-60.
- 16. Persic, M. and Salucci, P. (1990) Monthly Notices of the Royal Astronomical Society, 245, 577-581.
- 17. Carignan, C., Charbonneau, P., Boulanger, F. and Viallefond, F. (1990) Astronomy & Astrophysics, 234, 43-52.
- 18. Casertano, S. and van Gorkom, J.H. (1991) The Astronomical Journal, 101, 1231-1241.
http://dx.doi.org/10.1086/115759 - 19. Broeils, A.H. (1992) Dark and Visible Matter in Spiral Galaxies. PhD Thesis, University of Groningen, Groningen.
- 20. Persic, M. and Salucci, P. (1995) Astrophysical Journal Supplement, 99, 501.
http://dx.doi.org/10.1086/192195 - 21. Persic, M., Salucci, P. and Stel, F. (1996) Monthly Notices of the Royal Astronomical Society, 281, 27-47.
http://dx.doi.org/10.1093/mnras/278.1.27 - 22. Salucci, P. and Persic, M. (1997) Dark Halos Around Galaxies. In: Salucci, P. and Persic, M., Eds., Dark and Visible Matter in Galaxies, ASP Conference Series, Vol. 117, Astronomical Society of the Pacific, San Francisco, 1.
- 23. Milgrom, M. (1983) Astrophysical Journal, 270, 365-370.
http://dx.doi.org/10.1086/161130 - 24. Milgrom, M. (1983) Astrophysical Journal, 270, 371-389.
http://dx.doi.org/10.1086/161131 - 25. Milgrom, M. (1983) Astrophysical Journal, 270, 384.
http://dx.doi.org/10.1086/161132 - 26. Tohline, J.E. (1983) Stabilizing a Cold Disk with a 1/r Force Law. In: Athanassoula, E., Ed., Internal Kinematics and Dynamics of Galaxies, IAU Symposium 100, Reidel, Dordrecht, 205.
- 27. Felten, J.E. (1984) Astrophysical Journal, 286, 3-6.
http://dx.doi.org/10.1086/162569 - 28. Sanders, R.H. (1984) Astronomy & Astrophysics, 136, L21-L23.
- 29. Sanders, R.H. (1986) Monthly Notices of the Royal Astronomical Society, 223, 539-555.
http://dx.doi.org/10.1093/mnras/223.3.539 - 30. Mannheim, P.D. and Kazanas, D. (1989) Astrophysical Journal, 342, 635-638.
http://dx.doi.org/10.1086/167623 - 31. Christodoulou, D.M. (1991) Astrophysical Journal, 372, 471-477.
http://dx.doi.org/10.1086/169992 - 32. Mannheim, P.D. and O’Brien, J.G. (2011) Physical Review Letters, 106, Article ID: 121101.
http://dx.doi.org/10.1103/PhysRevLett.106.121101 - 33. Mannheim, P.D. and O’Brien, J.G. (2012) Physical Review D, 85, Article ID: 124020.
http://dx.doi.org/10.1103/PhysRevD.85.124020 - 34. Gallagher III, J.S., Hunter, D.A. and Tutukov, A.V. (1984) Astrophysical Journal, 284, 544-556.
http://dx.doi.org/10.1086/162437 - 35. Mestel, L. (1963) Monthly Notices of the Royal Astronomical Society, 126, 553-575.
http://dx.doi.org/10.1093/mnras/126.6.553 - 36. Jalali, M.A. and Abolghasemi, M. (2002) Astrophysical Journal, 580, 718-724.
http://dx.doi.org/10.1086/343849 - 37. Binney, J. and Tremaine, S. (1987) Galactic Dynamics. Princeton University Press, Princeton.
- 38. Schulz, E. (2012) Astrophysical Journal, 747, 106.
http://dx.doi.org/10.1088/0004-637X/747/2/106 - 39. Watson, G.N. (1922) A Treatise on the Theory of Bessel Functions. Cambridge University Press, Cambridge.
- 40. Christodoulou, D.M., Graham-Eagle, J. and Katatbeh, Q.D. (2016) Advances in Difference Equations, 2016, 48.
http://dx.doi.org/10.1186/s13662-016-0774-x - 41. Robe, H. (1968) Annales d’Astrophysique, 31, 549-558.
- 42. Schmitz, F. and Ebert, R. (1986) Astronomy & Astrophysics, 154, 214-218.
- 43. Schneider, M. and Schmitz, F. (1995) Astronomy & Astrophysics, 301, 933-940.
- 44. Christodoulou, D.M. and Kazanas, D. (2007) Exact Solutions of the Isothermal Lane-Emden Equation with Rotation and Implications for the Formation of Planets and Satellites. arXiv:0706.3205v2.
- 45. Christodoulou, D.M., Katatbeh, Q.D. and Graham-Eagle, J. (2016) Journal of Inequalities and Applications. (In Press)
- 46. Lane, J.H. (1870) American Journal of Science and Arts, Second Series, 50, 57-74.
- 47. Emden, R. (1907) Gaskugeln. B.G. Teubner, Leipzig.
- 48. Stodólkiewicz, J.S. (1963) Acta Astronautica, 13, 30-54.
- 49. Ostriker, J. (1964) Astrophysical Journal, 140, 1056.
http://dx.doi.org/10.1086/148005 - 50. Horedt, G.P. (2004) Polytropes. Kluwer Academic Publishers, Dordrecht.
- 51. Schmid-Burgk, J. (1967) Astrophysical Journal, 149, 727.
http://dx.doi.org/10.1086/149305 - 52. Chandrasekhar, S. (1939) An Introduction to the Study of Stellar Structure. University of Chicago Press, Chicago.
- 53. Hayashi, C., Narita, S. and Miyama, S.M. (1982) Progress of Theoretical Physics, 68, 1949-1966.
http://dx.doi.org/10.1143/PTP.68.1949 - 54. Narita, S., Kiguchi, M., Miyama, S.M. and Hayashi, C. (1990) Monthly Notices of the Royal Astronomical Society, 244, 349-356.
- 55. Schmitz, F. (1986) Astronomy & Astrophysics, 169, 171-177.
- 56. Kamp, I., Freudling, W., Robberto, M., Chengalur, J. and Keto, E. (2008) Physica Scripta, 2008, Article ID: 014013.
http://dx.doi.org/10.1088/0031-8949/2008/T130/014013 - 57. Williams, J.P. and Cieza, L.A. (2011) Annual Review of Astronomy and Astrophysics, 49, 67-117.
http://dx.doi.org/10.1146/annurev-astro-081710-102548 - 58. Belloche, A. (2013) EAS Publications Series, 62, 25-66.
http://dx.doi.org/10.1051/eas/1362002 - 59. Tobin, J.J., Hartmann, L., Chiang, H.-F., Wilner, D.J., Looney, L.W., Loinard, L., Calvet, N. and D’Alessio, P. (2012) Nature, 492, 83-85.
http://dx.doi.org/10.1038/nature11610 - 60. Tobin, J.J., Hartmann, L., Chiang, H.-F., Wilner, D.J., Looney, L.W., Loinard, L., Calvet, N. and D’Alessio, P. (2013) Astrophysical Journal, 771, 48.
http://dx.doi.org/10.1088/0004-637X/771/1/48 - 61. Yen, H.-W., Koch, P.M., Takakuwa, S., Ho, P.T.P., Ohashi, N. and Tang, Y.-W. (2015) Astrophysical Journal, 799, 193.
http://dx.doi.org/10.1088/0004-637X/799/2/193 - 62. Yen, H.-W., Takakuwa, S., Koch, P.M., Aso, Y., Koyamatsu, S., Krasnopolsky, R. and Ohashi, N. (2015) Astrophysical Journal, 812, 129.
- 63. Schmitz, F. and Ebert, R. (1987) Astronomy & Astrophysics, 181, 41-49.
- 64. Schmitz, F. (1988) Astronomy & Astrophysics, 200, 120-126.
- 65. Tohline, J.E. (2002) Annual Review of Astronomy and Astrophysics, 40, 349-385.
http://dx.doi.org/10.1146/annurev.astro.40.060401.093810 - 66. Tsitali, A.E., Belloche, A., Commerçon, B. and Menten, K.M. (2013) Astronomy & Astrophysics, 557, A98.
http://dx.doi.org/10.1051/0004-6361/201321204 - 67. Marr, J.H. (2015) Monthly Notices of the Royal Astronomical Society, 448, 3229-3241.
http://dx.doi.org/10.1093/mnras/stv216 - 68. Newton, I. (1687) Philosophæ Naturalis Principia Mathematica. S. Pepys, Reg. Soc. Praesses, London.
- 69. Magain, P. and Chantry, V. (2013) Gravitational Lensing Evidence against Extended Dark Matter Halos. arXiv: 1303.6896.
- 70. Jordi, K., Grebel, E.K., Hilker, M., Baumgardt, H., Frank, M., Kroupa, P., Haghi, H., Côté, P. and Djorgovski, S.G. (2009) The Astronomical Journal, 137, 4586-4596.
http://dx.doi.org/10.1088/0004-6256/137/6/4586 - 71. Lane, R.R., Kiss, L.L., Lewis, G.F., Ibata, R.A., Siebert, A., Bedding, T.R. and Székely, P. (2009) Monthly Notices of the Royal Astronomical Society, 400, 917-923.
http://dx.doi.org/10.1111/j.1365-2966.2009.15505.x - 72. Lane, R.R., Salinas, R. and Richtler, T. (2015) Astronomy & Astrophysics, 574, A93.
http://dx.doi.org/10.1051/0004-6361/201424074 - 73. Moni Bidin, C., Carraro, G., Mendez, R.A. and Smith, R. (2012) Astrophysical Journal, 751, 30.
http://dx.doi.org/10.1088/0004-637X/751/1/30 - 74. Moni Bidin, C., Smith, R., Carraro, G., Mendez, R.A. and Moyano, M. (2015) Astronomy & Astrophysics, 573, A91.
http://dx.doi.org/10.1051/0004-6361/201424675 - 75. Lelli, F. (2014) Galaxies, 2, 292-299.
http://dx.doi.org/10.3390/galaxies2030292 - 76. López-Corona, O. (2015) Journal of Physics: Conference Series, 600, 012046.
- 77. Huygens, C. (1690) Treatise of Light. Pierre van der Aa, Leyden.
- 78. Michelson, A.A. and Morley, E.W. (1887) American Journal of Science, 34, 333-345.
http://dx.doi.org/10.2475/ajs.s3-34.203.333 - 79. Huré, J.-M., Hersant, F., Carreau, C. and Busset, J.-P. (2008) Astronomy & Astrophysics, 490, 477-486.
http://dx.doi.org/10.1051/0004-6361:200809682 - 80. Myers, P.C. (2009) Astrophysical Journal, 700, 1609-1625.
http://dx.doi.org/10.1088/0004-637X/700/2/1609 - 81. Fischera, J. and Martin, P.G. (2012) Astronomy & Astrophysics, 542, A77.
http://dx.doi.org/10.1051/0004-6361/201218961
Appendix: Vertically Thin Discs Versus Infinite Cylinders
When applied to the equatorial planes (

where

The analysis presented in Sections 3 and 4 shows that the specific enthalpy in cylinders assumes a logarithmic radial profile (Equation (14)). Now, pressure is an isotropic force and its nature is to push spherically out in self- gravitating gases. Therefore, Equation (14) suggests that, in axisymmetry, the specific enthalpy of the gas could assume the spherical form

where r is the spherical radius normalized by
1) Applying the radial (x) component of the cylindrical Laplacian to Equation (24) and then setting
2) Taking the derivative with respect to z in Equation (24) and then setting




3) Combining Equations (23) and (24), we find that

This is the term that was ignored for discs in the radial force balance described by Equation (12). But it makes only a minor contribution to the force balance over all radii where

where 







where B is the integration constant. We see now that the dimensionless mass per unit length

makes the largest contribution to the rotation curve. Neglecting the term

For 









Similar results can also be obtained for Equations (3) and (4) in which the inertial terms 





On the other hand, the models in [79] with steep power-law surface densities (


where 

We argue that all other razor-thin models that do not satisfy Gauss’s law at 


Rising rotation curves were also found by Marr [67] who studied models in which 1/x surface density profiles were truncated at a radius near the last observed point. By not being there to pull outward, the exterior mass allowed the inward force due to the interior mass to amplify, and this caused the rotation curves to turn up near the peripheries of the discs, despite the fact that these were essentially Mestel discs. In any case, our analytic solutions (Sections 3 and 4) avoid the above pitfalls (mixing of homoeoids of different sizes, truncation creating sharp edges); and they show that the volumetric density at all equatorial radii is always sufficient to continue pulling the rotation curves higher.
For 

1) In all isothermal models with 
Equation (27) is positive definite. Then 


curves rise at all radii as more interior mass is added incrementally by the radial integration with increasing x.
2) On the other hand, in the isothermal models with 









Returning to the pressure term (



Our analysis in Sections 3 and 4 was carried out without the 
NOTES
1The periodic solution found in [51] describes a Cartesian slab and not a disc or cylinder.
2We note in passing that, as a result of the substitution 
3In the case of the Class 0 young system L1527 [59] [60] , the rotation curve is not flat, but we did not catch this 0.3 Myr old system early enough (the sound-crossing time at 100 AU for a 10 K cold gas with Co = 0.3 km∙s−1 is 1500 yr). On the other hand, Yen et al. [61] [62] report several other Class 0 YSOs whose rotation is not Keplerian outside of the inner few AU.
4When a protostar grows at the center of a protoplanetary disc, the enthalpy is defeated by gravity because the enthalpy cannot source and manipulate this component of the gravitational field via the Poisson equation (see Section 3.1); and the intrinsic solutions described in this work are no longer valid for such gaseous discs subject to “external” gravitational fields.











