Received 16 October 2015; accepted 20 December 2015; published 23 December 2015

ABSTRACT

In this work, we reveal possibility using information soliton to resist senescence of certain important bio-excitations (such as Davydov solitons) which play a fundamental role in information processing of life. For this goal, a type of external field interaction with original system is introduced. This field enables the total system to be described by a nonlinear Master equation. Then we found that the nonlinear term in the equation drives the initial excitation to evolve as a kind of information soliton asymptotically. It is this information soliton to resist decaying of the excitations. This provides a constructive way to prolong age of biological excitations by exerting an external field, which forms a basis used in medical devices or treatments.

Keywords:

Quantum Information Density, Master Equation, Nonlinearity

1. Introduction

The fundamental transmission of energy and information in bio-systems including human body is an important issue since many bio-processes are related to this sort of transmissions. In early 1973 Davydov has proposed protein molecules excited “solitary” model of the energy transport [1] . According to his theory, three spiral micro-vibration and lattice distortion of amide-I exciton in a protein molecule produce collective excitations to form a soliton, along the helix propagation, so that ATP molecules hydrolyze to produce energy from one place to another place. This can be found in the experiment that soliton resonance light decomposes into excitons and local deformation, corresponding to a new band in 1650 cm⁻¹, with amide-I exciton infrared absorption spectra observed on the 1666 cm⁻¹ line. This proves that there is a red shift of 16 cm⁻¹ corresponding to the formation of just soliton bound energy. However, Davydov soliton seeming to have short-time circle is serious obstacle to explain why it is a basic unit of energy and information transmission in bio-systems. For improving this weakness of the model, many scholars proposed modified models [2] . After that, Pang Xiaofeng improved and developed Davydov soliton model with longer life span and established a frame of biological soliton transmission theory based on his nonlinear quantum theory [3] [4] , by which Pang Xiaofeng shows that the revised Davydov solitons can play a basic metabolism role in energy and information transmission of bio-systems including human body. So, in some senses, the Davydov soliton transmission is so important so that if the Davydov solitons are damaged by dissipation the system should decay fast. This raised a problem, how to maintain our Davydov solitons in a health status by against dissipation? Or can one find an external field to act bio-systems to enable the Davydov solitons to remain longer with health status?

In fact, from ancient time until today, there exists various decaying of bio-systems. The behind principle is thermodynamic second law to rule the fundamental processes of lives. Although we cannot claim that a life system is a closed system, there exist undoubtable facts that the entropy in a life system finally increases to a maximum state, which is the main currency of life span because the dissipation naturally happens. Many years ago, Nobel laureate Prigogine introduced the negative entropy [5] [6] , which is just a kind of expression of information, to permit a self-organization to grow by against dissipative decaying in the evolution of open system. However, the microscopic mechanism of the theory is still required to clarify and develop, especially in the quantum information (entropy) level. Therefore studying the informational character of the density operator for the Liouville equation may be a novel angle. In previous works [7] [8] we have found that the Liouville equation

is still correct for quantum information density (QID), i.e., where corresponds to a

sort of general QID, and especially, 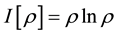is defined as QID which is just negative quantum entropy density. This reveals that, in some senses, the density operator can be considered as a minimum unit of QID [9] -[15] .

Concerning with above background, in this work, we study how to use a suitable external field to interact with an original Davydov solitons system to prolong life of solitons. In this study, we find that the total system can be described by a sort of nonlinear Master equation. The asymptotic solution of the equation can be defined as an information soliton that can be used to resist dissipative decaying of the Davydov solitons. This provides a possible mechanism using an external field to prolong life of the Davydov solitons.

2. Nonlinear Excitations of Life

For make sense, we firstly consider a biological system with many nonlinear excitations as the Davydov solitons modified by Pang Xiaofeng [16] or various Davydov solitons in the transmission of gens systems or nerve systems, and so on [17] [18] . These Davydov solitons (or nonlinear excitations) represent local nonlinear oscillations having characteristics of quasi particles, which can carry basic information and energy to transmit in organization, for simplicity, here we study the evolution of a Davydov soliton which merges into a thermo-pho- tonic field, the relevant Hamiltonian can be written as

(1)

where is a creation (annihilation) operator of the Davydov soliton, 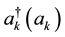is the creation (annihilation) operator of photon with wave vector k, 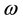represents frequency, and 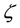represents a coupling number. Then one has

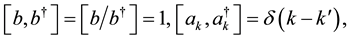(2)

and

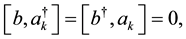(3)

where notice is the nonlinear operator which describes the Davydov soliton, hence the commutation relation is redefined by

(4)

with

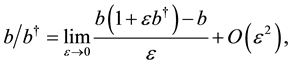(5)

is called the Slash product which allows the nonlinear operator b, to have the product properties as the linear operator [19] . Therefore the following treatment and main results obtained for the nonlinear operator b, are similar to that of linear operator except the Slash product implied in the formalism.

3. Nonlinear Master Equation

Indeed, considering above Hamiltonian, a Master equation [20] which describes the decoherent and dissipative processes can be established as

(6)

where defining a damping number

(7)

and () is an coefficient of absorption (emission) of photos (or phonons) for the Davydov soliton, respectively. Then the formal evolution of the density operator can be given by

(8)

which is expressed by means of left multiplying, namely

(9)

where is a coherent and entangled state as a basis introduced by Fang Hongyi [21] . Then one can see, there are decaying factor and increased factor in the evolution, however the total effect on the state of the Davydov soliton is still decaying, i.e.

(10)

until final state tends to a status corresponding to the maximum entropy induced by the thermodynamical second law.

How can one change this decaying? One idea presented in this work is to introduce a field coupling to the system, which allows the Master equation to increase a self-interaction term which can wipe the dissipative decaying. Through observation, here a field can be design to synchronize with through a sort of resonance between and, namely

(11)

with

(12)

where g is a coupling number, is defined as a scalar product,

(13)

is a integral measure. This enables the original damping Master equation to become

(14)

Then let

(15)

one gets

(16)

where denote () is a creation (annihilation) operator which acts on the thermostats introduced by Takahashi and Umezawa [22] [23] . Consequently, there exist transformations, , and by acting on the state, which allows f to commute with the thermostats to arrive at Equation (16). Thus a formal solution of this equation can be constructed as

(17)

which gives

(18)

where defining as

(19)

and corresponds to time.

Thus, by considering Equation (8), Equation (18) can change to

(20)

Using the relations [22] [23] and following the methods in [21] :

(21)

and left acting the state into Equation (20), Equation (20) becomes

(22)

which allows one to get as

(23)

where the relevant parameters, , and are defined as

(24)

and the related integral formula is used as

(25)

Then the Kraus sum representation [24] of the density operator is deduced by

(26)

where the Kraus operator is expressed as

(27)

where denote

(28)

This enable one to gain an asymptotic solution as

(29)

where is defined as

(30)

with

(31)

Therefore an asymptotic solution is achieved as

(32)

This asymptotic solution is define as a sort of information soliton [25] in the sense: 1) it is an invariant structure of the density operator (with information density meaning mentioned in the introduction) locally when time elapses enough long, 2) this structure appears only through self-interaction of the density operator in an open system. The study of asymptotic evolution of this structure may shed more light on the soliton dynamic behavior of information density for long time, as in this quantum channel the asymptotic configuration can be determined by the spectral decomposition of the evolution operator and the decoherence-free formation can also appear by the kind of nonlinear self-interaction of the information density reduced from environment. We want to emphasize that the information solitons obtained here is an asymptotic stable structure of density operator (as a sort of minimum unit of QID mentioned in the introduction) due to the nonlinear self-interaction induced from non-equilibrium of QID between system and environment, which is different from the various solitons consisting of wave functions.

4. Information Soliton

Through observing, the above solution can be extended as a general solution for,

(33)

which matches up the equation

(34)

Consequently, by introducing an expansion

(35)

one can construct a nonlinear master equation with a complicated term as, i.e.

(36)

As a result (and also considering Equation (33)), the solution of above equation can be constructed by

(37)

where defining

(38)

This allows one to obtain

(39)

which shows that one can adjust the coupling field R to obtain desired

(40)

For example, if let satisfy

(41)

then one attains

(42)

So, in terms of the above results, the key to choose a field is that has a synchronized resonance with, where is a Davydov soliton expressed approximately as. Therefore one of the wave functions for ideal may be chosen as

(43)

where can be considered as exciton part of the field and can be considered as phonon part of the field. In fact, a series of studying the energy transfer mechanism and characteristics of the Davydov soliton [3] [16] [26] show that the absorption of infrared line can cause quantum vibration in the protein amide bond, while the vibrational protein molecules of the amide bond can and can only absorb or emit infrared line as or. Furthermore, the existence of acoustic wave with can also be calculated by study of the Davydov soliton model. This motivates us to adopt a combination of an infrared and acoustic waves field as to realize synchronized resonance with particle density of the Davydov soliton. Where, the acoustic wave may be generally chosen to close, for, while the infrared wave may be generally chosen to close, for.

5. Conclusion

A type of nonlinear Master equation which describes the Davydov plus field system is investigated. The nonlinear term enables the initial excitation state to evolve to a sort of information soliton without decaying when time passes enough long. While the power of nonlinear term increase can be used to remain invariance of initial state of excitation. These two characteristics reveal a constructive mechanism to prolong life span by using adjustable field which has a synchronized resonance with original solitons. One of possible fields is a combination of infrared and acoustic field with infrared line as or, and acoustic frequency as, which may provide a basis using the field to perform various medical treatments.

Acknowledgements

The authors thanks for the support from the fund of Wuhan University of Technology.

Cite this paper

QiaoBi,KongzhiSong, (2015) A New Information Soliton to Resist Decaying of the Excitation Based on the External Field Interaction. Journal of Modern Physics,06,2211-2218. doi: 10.4236/jmp.2015.615225

References