Received 14 July 2015; accepted 14 November 2015; published 17 November 2015

ABSTRACT

A certain class K of GR homogeneous spacetimes is considered. For each pair E, 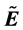of spacetimes from K, 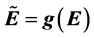where conformal transformation g is from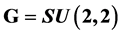. Each E (being 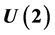or its double cover, as a manifold) is interpreted as related to an observer in Segal’s universal cosmos. The definition of separation d between E and 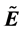is based on the integration of the conformal factor of the transformation g. The integration is carried out separately over each region where the conformal factor is no less than 1 (or no greater than 1). Certain properties of 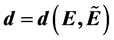are proven; examples are considered; and possible directions of further research are indicated.

Keywords:

Separation between Spacetimes, Segal’s Universal Cosmos, Conformal Group Action on U(2), DLF-Theory

1. Motivation and Introduction

The first author has been interested in GR (“GR” is for General Relativity) research for quite a while and he concentrated on a few most symmetric spacetimes ( [1] , [2] , and more). Later (see [3] , [4] ) he has become a strong believer in Segal’s Chronometric Theory (see [5] , electronic archive arranged by Levichev), and he is attempting to modify Segal’s Theory (see [6] , a key publication). The collaboration of the two current authors is based on their mutual interest in Penrose-Hameroff approach to consciousness (see its update in [7] , [8] ). Specifically, we are putting forward an alternative definition of separation between space-times. In [9] , the original definition was based on bringing up a Newtonian limit in GR. Our definition has been introduced in [10] , [11] , and we now present it in much more detail.

Recall the Lie group 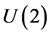as the totality of all two-by-two matrices z (with complex entries allowed) satisfying

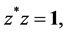(1.1)

where 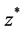is the transpose and complex conjugate of z, and is the unit matrix. Now, define the Lie group 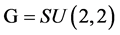as consisting of all four-by-four matrices g (with complex entries allowed) satisfying

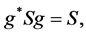(1.2)

where S is the diagonal matrix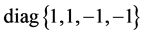. Recall the well-known linear-fractional G-action on:

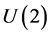(1.3)

where a matrix g from G is determined by its blocks A, B, C, D.

In Table I of [12] , the matrices are chosen as basic vectors of the (fifteen-dimensional) Lie algebra, whereas are the corresponding vector fields on. The vector fields are determined by the G-action (1.3). As explained in [12] , subscripts i, j take on −1, 0, 1, 2, 3, 4, and the convention (resulting in) holds.

The Lorentzian inner product on is introduced in such a way that left-invariant vector fields form an orthonormal basis (following [12] , we use +, −, −, − signature). The resulting product on is bi-invariant (see [6] ), and below denotes the Lorentzian inner product of tangent vectors at a point z of. The spacetime thus obtained is denoted by (the meaning of the subscript will become clear in the next section). Transformations (1.3) are conformal in (a word of caution: this spacetime has been denoted as D in [6] ). As it follows from Table I of [12] , the vector fields, generate isometries in. The corresponding subgroup K in G consists of all matrices (1.2) with.

For what follows, it is instrumental to introduce a certain bi-invariant Riemannian inner product on. To do so, we recall that vector fields constitute a basis of the Lie algebra. This algebra is a direct sum of its center with. Namely, generates the center, whereas, , are basic vectors in. The Riemannian metric is determined by the demand on left-invariant vector fields, , , to form an orthonormal basis. The corresponding Riemannian space is denoted. Again, is, as a manifold. Our below denotes the Riemannian inner product of tangent vectors at a point z of. In the forthcoming sections the corresponding volume form on will be instrumental. From Table I of [12] , it follows that the group K acts as a group of both Lorentzian and Riemannian isometries.

Notice that, as a group, is not a direct product of its center with the subgroup. The double cover of is the direct product (with represented by). The covering map sends into the matrix in. The corresponding Lorentzian metric on is of the form

(1.4)

Here the variable t is along whereas is for the standard Riemannian metric on. More details are given in our Appendix A, where u denotes a matrix from. Our Appendix B is dedicated to a certain one-parameter group of transformations (1.3).

It is well-known ( [12] , [13] ) that the (above introduced) covering map is a Lorentzian isometry. Infinitesimal G-action on is presented in Table I of [12] . It is known (see [13] ) that action (1.3) can be lifted to a global conformal G-action on. Using the corresponding commutative diagram, one can show that the lifted action of the group K is as follows:

(1.5)

Also, it is easily verifiable that for the Riemannian metric

(1.6)

on the (above specified) covering map is a Riemannian isometry from onto.

It makes sense to mention how a suitable version of the Einstein static universe, , can be introduced in the context of our work (the subscript uc is for universal cover). To be more precise, should be called universal cosmos ( [14] ) or Segal’s universal cosmos ( [13] ). The universal cover of is, topologically. The G-action on is canonically lifted to the G_uc-action on (the latter action preserves the causal structure of). In a cosmological model based on, there is a conformal invariant R, interpreted as the radius of a three-dimensional (physical) space. I. Segal (in [14] and in other publications) has put this R for the (long wanted by Dirac and others) third fundamental constant additionally to the speed of light and to the Planck’s constant. It is known that to model particles on, one can start with the world, a compact one. The respective property is called automatic periodicity ( [15] , p. 202), and it allows us to only deal with compact spacetimes and (which explains our compact Segal’s cosmos terminology).

More precisely, we deal with two classes of spacetimes: and. Roughly speaking, the first class is obtained by application of all transformations (3) to; details follow in the next section (where will also be defined).

2. On the Notion of Separation between Spacetimes: The Main Definition and Related Properties

The separation (or distance) will be defined for any pair x, y of spacetimes from (or from).

As mentioned, the totality of all isometries in is the group K of all matrices (1.2) with. Each member E of the class will be now put in correspondence with an element x of the homogeneous space

G/K. Namely, each element (or coset) x of G/K is specified by an element g from G:. One and the same x can be determined by another element (say,) from G: gK = g₁K. For such a pair,

there exists such k from K, that. When the subgroup K is viewed as an element of G/K, denote K as. This we put into correspondence with (which has been described in Section 1). As a manifold, each element x of is. In what follows, we use (rather than) to denote the (Lorentzian) inner product of vectors from the tangent space T(E₀) at z. This inner product has been introduced in our Section 1. To define spacetime E corresponding to a coset x = gK, it is enough to specify the inner product

, see (2.2) below. Such a transformation g is conformal in E₀. Namely, given vectors from the tangent space T(E₀) at z, the inner product at of their images (under the tangent map) satisfies

(2.1)

The everywhere positive function is known as the square of conformal coefficient. Frequently, we will simply refer to this as to a conformal coefficient. Given vectors from the tangent space at z, their inner product can be defined as follows:

(2.2)

where is calculated at z. Notice, that h here is the (above mentioned) function on determined by g It is easy to show that (2.2) is equivalent to the condition for g to be an isometry between and:

(2.3L)

Here the right hand side of (2.3L) is calculated in at z, and it defines the inner product of vectors and at. To avoid verification of (2.2)-(2.3L) equivalence, we define the Lorentzian metric in E in terms of (2.3L). Similarly, we define the following Riemannian metric in E:

(2.3R)

where the positive definite inner product in the right hand side of (2.3R) has been introduced in our Section 1.

Let us show that, given a coset x in G/K, (2.3L) correctly defines a Lorentzian metric on, whereas (2.3R) correctly defines a Riemannian metric on:

Scholium 2.1. The inner product (2.3L) (respectively, the inner product (2.3R)) is independent of the choice of g which represents a coset x.

Proof. If x is represented as g₁K, then where k is a certain element of the group K. Given such a representation, the analogue of (2.3R) is

(2.4)

where the right hand side of (2.4) is calculated in at z, and it defines the inner product of vectors and at. We have to show that (2.4) introduces the same metric structure on as (2.3L) does. To do so, we rewrite (2.3L) in the form of

(2.5)

where the right hand side is calculated at, and the left hand side is calculated at.

However, in (2.5) equals in (2.4) since k is a Lorentzian isometry in. Comparison of (2.4) with (2.5) finishes the proof. The verification process, that (2.3R) is independent of representative, copies the one for (2.3L). □

Let us notice (see [16] ) that each can be interpreted as a spacetime corresponding to a certain (global) observer. A word of caution: [16] treats the universal cover of whereas we only deal with compact spacetimes here.

Remark 2.2. We have thus defined the class of spacetimes. Our class can be similarly introduced in terms of the Lorentzian manifold (the 2-cover of) with the (lifted) G-action on.

Given a (1.3)-transformation g of (Lorentzian), define the following subsets of:

(2.6)

(2.7)

here is the square of the conformal coefficient at z of the transformation g. A (non-negative) number is defined as follows:

(2.8)

where is for the volume of a set S in (with the volume form introduced in our Section 1). Clearly, expressions inside the logarithms in (2.8) can be interpreted as corresponding cumulative distortions of the original metric structure in. To be sure of convergence of all of the integrals involved, it is enough to mention that each of the two integrands is a continuous function over the corresponding region of integration, whereas each of the regions (2.6), (2.7) is a compact set.

To further deal with (2.8), we now proceed with more technicalities. Clearly, can be viewed as with,. The integration in a is over, whereas in c the integration is over.

Examples of integrals evaluations are given in our Appendix C (see Theorem C.5). Notice that

(2.9)

which follows from (2.8) because in this case, a constant function on. As a result of, each of the two terms in the sum (2.8) is zero.

Scholium 2.3. Given the (1.3)-transformation g and isometries, , the following holds:

(2.10)

where.

Proof. To prove (2.10), we will now show that each of the four numbers (a, b, c, and d) remain the same when we switch from to. Namely:

Similarly,. Hence, , and, due to the K-invariance of the volume form.

Let us now use the variable in the integral a of over: the integrand is then

, the region of integration is, and there is no extra factor in the

integrand since is a transformation from the group K. Similarly, number c remains the same when we switch from to. □

Now, if two cosets are represented as, , define the distance as

(2.11)

where. The number is independent of representatives since if x is represented by, and y is represented by, then for, according to (2.10).

Corollary 2.4. In the above settings, where and.

A word of caution: we use the term distance but we are not sure that the corresponding triangle inequality holds (even locally) for (2.11). However, we prove (below) that (2.11) is symmetric:, and G-invariant:

(2.12)

for arbitrary f from G (where we have in mind the canonical action of G in G/K).

As regards G-invariance, one can think of a possible relation of our definition (2.11) to the canonical inner product in the symmetric space G/K. This we do not discuss here.

Scholium 2.5. The distance (2.11) is symmetric:.

Proof. As justified by our Corollary 2.4, assume that and. Define

where, and where we use (rather than z, as before) to denote a matrix in. Tilde (below) indicates that computations are performed in E rather than in.

For the following is true:

since, due to (2.3R), g is an isometry between the two Riemannian spaces. Similarly,. The new integrand is then, the new region of integration is, and there is no extra factor in the integrand since g is an isometry between the two Riemannian spaces in question. We have thus proven that. Similarly,. We have thus proven the equality, which results in, the symmetry property of the distance between spacetimes. □

3. Concluding Remarks and Future Research Insights

Examples of integrals evaluations (in case of a certain one-parameter group of conformal transforma- tions) are given in our Appendix C. It is of interest to know whether Theorem C.5 holds for other transforma- tions from G =. Evaluations in Appendix C indicate that definition (2.11) of distance between spacetimes seems to be quite a working one. As part of future research, it will be of interest to apply our definition in the case where the original spacetime is F (here we refer to the DLF-theory, [6] ). In that case, the underlying manifold is (non-compact!), rather than. Preliminary calculations indicate that a conformal coefficient might be unbounded. We will thus have to deal with improper 4D integrals, and the question of convergence will have to be studied first.

Cite this paper

Alexander Levichev,Andrey Palyanov, (2015) On Separation between Metric Observers in Segal’s Compact Cosmos. Journal of Modern Physics,06,2040-2049. doi: 10.4236/jmp.2015.614210

References

Appendix A: Parameterizations of U(2) and E⁽²⁾

The following presentation for E⁽²⁾, the 2-cover of, has been widely used in the literature. Consider the direct sum E⁶ = E² Å E⁴ of two Euclidean spaces: E² with rectangular coordinates, , and E⁴ with rectangular coordinates. Each “event” in E⁽²⁾ is a 6-tuple, satisfying

(A1)

and

(A2)

Clearly, E⁽²⁾ is S¹ × S³, topologically. The earlier introduced (see Section 2) is, whereas the matrix u from is specified as follows:

(A3)

The covering map from E⁽²⁾ onto takes the pair into the matrix, an element z of the group:

(A4)

Given a matrix z in, the factors and u are defined up to a sign, only. In terms of E⁶, it is helpful to consider a pseudo-Euclidean metric

(A5L)

and an Euclidean metric

(A5R)

It is known (see [14] , p. 40) that the restriction of (A5L) onto E⁽²⁾ = S¹ ´ S³ coincides with metric (1.4) of our Section 1. Similarly, the restriction of (A5R) onto E⁽²⁾ coincides with metric (1.5).

Appendix B: The Case of a Certain One-Parameter Group of Conformal Transformations

This group consists of all (1.3)-transformations g of the form:

(B.1)

with

where, , being a real parameter. This subgroup is contained in a (two-dimensional) subgroup A (from the Iwasawa decomposition = KAN). The below is for the (positive) square root of the conformal factor. The latter has been defined by our (2.1). To simplify notation, we, sometimes, use the same symbol (like z or, below) to denote both an element of E⁽²⁾ and a matrix in E₀. The statement and the proof of the following theorem presume usage of rectangular coordinates in Euclidean E⁶: see Appendix A.

Theorem B.1. The image of z in E⁽²⁾ and the conformal factor at z (under the lift of the (B.1)― transformation g) are as follows:

(B.2)

(B.3)

Proof. Notice that due to (A3) and (A4) from Appendix A, the formulas (B.2) correctly define the transformation on the level of E₀ (when z and are matrices). To prove this first part, we use (B.1) in a straightforward way and (omitting routine details of the calculation) determine (B.2). At this stage of the proof we cannot be sure that is the conformal coefficient. To prove that it is, apply the differential operator d to both sides of (B.2) in order to express

(B.4)

in terms of differentials, , , , ,. Comparison of the obtained expression with (A5L) verifies (B.3). □

Remark B.2. In the case considered, there is an alternative way to determine the conformal factor (B.3). It is as follows [17] , Theorem 3: for a (1.3)-transformation g, the following equality holds for the conformal factor at z:

(B.5)

One can verify that (B.5), when applied in the (B.1)-case, results in (B.3).

It is of interest to determine all fixed points (that is, matrices with property) of the transformation (B.1).

Scholium B.3. The totality of all fixed points of (B.1) is a pair of circles. One of the circles is given by equations,. The other circle is given by equations,.

Proof. As it follows from (B.1), the totality of all fixed points is the solution set of

(B.6)

equality of two matrices. Comparison of first entries in second rows results in

(B.7)

Since g is not an identity transformation,. If, then comparison of first entries in the first rows results in, that is,. Comparison of second entries in second rows results in. Now, if in (B.7), then, again,. □

Our next goal is to prove that each fixed point (of a given (B.1)―transfor-mation) is an extreme point of the conformal coefficient: maximum is reached at each point of one circle whereas minimum is reached at each point of the other circle.

Scholium B.4. If at, then is not a point of extremum for.

Proof. If at, then, can be chosen as two (of the total of four) free real variables at the vicinity of. If is a point of extremum for, then each of the two partial derivatives of h (w.r.t., and w.r.t.) vanish at. However, that would have resulted in vanishing of at. □

Corollary B.5. If is an extreme point for h, then (that is,).

Corollary B.6. At the point of extremum for the conformal coefficient, either, or (that is, , or).

Proof follows from the expression which holds at every point z where. □

Corollary B.7. An extreme value of is reached at if and only if is a fixed point of (B.1). One can verify that the two extreme values are and where is the (non-zero) value of the parameter in (B.1).

Appendix C: Evaluations of Integrals (2.8) for the Case of Appendix B Transformations in E⁽²⁾

We start with the form

(C.1)

on the torus T = S¹ ´ S³, see our Theorem B.1. Now, T⁺ is for the part of T where, T⁻ is for the part of T where. Introduce

(C.2)

(C.3)

where in both cases we have in mind the volume form which has been introduced on T in Section 2.

A word of caution: the function (C.1) is the inverse of the conformal coefficient (B.3). Nevertheless, the findings (which follow) of this Appendix C are relevant to the Appendix A content since k in (C.2), (C.3) can be any integer.

The majority of these Appendix C findings are due to V. V. Ivanov (Sobolev Institute of Mathematics, Novosibirsk, Russia).

Parameterize T as follows:

(C.4)

In terms of these parameters, (C.1) becomes

(C.5)

The integrals (C.2), (C.3) are reduced as follows:

(C.6)

where

(C.7)

Here we consider the rectangle, and,. Notice that the integrals (C.6) and (C.7) are independent of the sign of which allows us to stay with, only. The next step is to interpret, as polar coordinates on the x, y plane:

(C.8)

Our function (C.5) becomes

(C.9)

whereas, are to be converted into, with their union being the unit disc D centered at the origin (0,0) of the x, y plane. Finally, introduce coordinates r,:

(C.10)

r being the distance between and, whereas the angle, in radians, is an angle between vectors and PQ. Expression (C.9) becomes

(C.11)

Introduce an (acute) angle which is determined by any of the relations

(C.12)

Omitting a few more (straightforward) technicalities, we obtain

(C.13,C14)

The upper limits, are as follows:

(C.15,C.16)

Let us conclude in terms of the following statements.

Theorem C.1. For k not equal −1, the integrals (C.2), (C.3) can be evaluated as follows:

(C.17)

For k = −1

(C.18)

Theorem C.2. For every integer k,

(C.19)

Theorem C.3. For a nonnegative k, each of the integrals (C.17) is a finite linear combination of integrals, where

(C.20)

Remark C.4. Each of the integrals (C.20) is an elementary one and it can be expressed as a polynomial in s and.

Recall notations a, b, c, d of Section 2 (see the line prior to Formula (2.9)) for the integrals which are of our utmost interest.

Theorem C.5. The integrals a, b, c, d, are as follows:

,

,