Received 27 April 2015; accepted 20 June 2015; published 24 June 2015

ABSTRACT

Multifractal analysis is carried out for the interactions of 4.5 A and 14.5 A GeV/c ²⁸Si beams with emulsion, CNO and AgBr targets using the standard method of G_q moments. The Rényi dimensions D_q are evaluated and the results on self-similar multifractal spectra are presented. The variation of D_q with q is looked into and the findings reveal that the behaviour is in consistency with the multifractal characteristic of the multiplicity distributions in the various interactions studied. The self-similar multifractal spectra are found to be concave downwards with maximum at α_q = 0. Further, Lévy stability analysis is carried out for these interactions. The Lévy stability index μ extracted from multifractal spectrum is found to lie in the range [0, 2] in agreement with the Lévy stability theory.

Keywords:

Multifractal, Rényi Dimensions, Lévy Stability

1. Introduction

Study of high-energy nucleus-nucleus collisions may address several important issues concerning multiparticle production. Besides this, these collisions are envisaged to create conditions necessary for the production of quark-gluon plasma (QGP). Various studies [1] -[4] suggest the possibility of existence of a deconfined phase of matter comprising essentially of quarks and gluons at energy density ~3 GeV/fm³ with a subsequent phase transition to hadrons. Several important and fascinating signatures [5] for the production of QGP have been proposed. One of the various possible approaches is to investigate the fluctuations in particle densities. Such investigations are carried out with the realization that a phase transition may give rise to fluctuations in individual events which may manifest as clear peaks or spikes in the phase space domains [6] - [8] . In the case of hydrodynamic turbulence, this aspect is studied via scaling properties of the moments of the relevant distributions as functions of the bin sizes of the phase space [9] .

An attempt to investigate some important characteristics of the mechanism involved in multiparticle production is made by Bialas and Peschanski [10] , who have suggested the power law behaviour for the factorial moments as function of successively decreasing phase space bins which is referred to as intermittency. The search for a link between intermittency and a phase transition leads to a thermodynamic formulation of fractal dimensions of which intermittency is a special case [11] - [14] . A fractal or a self-similar object has the characteristic property of satisfying a power law scaling behaviour which reflects the underlying dynamics [15] . The multifractal nature of the produced particles in heavy-ion collisions is studied in terms of generalized Rényi dimensions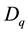. In the present study, the method of multifractal moments [15] is used to evaluate.

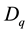It has been proposed [16] [17] that as a self-affine or a self-similar fractal system, the multiparticle final state in high energy collisions can be characterized by an important parameter―the Lévy stability index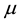. This parameter helps in classifying the intermittency regimes due to different kinds of phase transitions during cascading processes [18] . It has been suggested [19] that may be an indication of thermal phase transition whereas 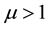corresponds to a non-thermal phase transition. According to the Lévy stability theory [20] , the Lévy index 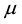is confined to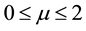. This parameter is also known as the degree of fractality, for monofractals, corresponds to “calm” singularities, whereas 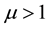refers to “wild” singularities [20] . In the present work, the Lévy stability index is extracted from the multifractal spectra using the approach formulated by Hu Yuan et al. [17] .

2. Mathematical Formalism

For studying multifractality, a given pseudorapidity range, , is divided into M bins of width. If denotes the particle multiplicity in the 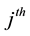bin, then the total number of particles in an event is estimated using the relation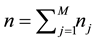. The fraction of particles in the j^th bin is given by:. Once this fraction is known, the order multifractal moment, , is defined [15] [21] as:

(1)

where the summation is carried out over the non-empty bins only which constitute a fractal set.

On averaging over all the events in a data sample consisting of events, is expressed as:

(2)

For the fractal nature of rapidity distribution, should exhibit the power law behaviour [22] over a range of small in the following fashion:

(3)

where are the mass exponents and may be determined using:

(4)

The spectral function, , which can be obtained [15] by Legendre transform by using the standard procedure of multifractals [22] is calculated from

(5)

where given by are referred to as the Lipschitz-Holder exponents [23] .

For a multifractal structure, the spectral function is a smooth function, concave downwards with its maximum at. The left and right wings of the plots of the function give a quantitative description of the fluctuation density in the dense and sparse regions of a single particle pseudorapidity distribution [21] - [23] . Inhomogeneity of the pseudorapidity distribution is determined by the width of the distribution. The non-exis- tence of a sharp peak in versus plot at corresponding to reveals non-smooth nature of the pseudorapidity distribution in the phase space [24] .

One of the most basic properties of the fractals which describe the scaling behaviour are the multifractal Rényi dimensions, , defined [25] as:

(6)

It may be of interest to note that if decreases with increasing q, the pattern is known as multifractal and on the other hand, if is constant, the pattern is referred to as monofractal [25] [26] .

The order multifractal Rényi dimensions can also be obtained from the multifractal spectrum through [9]

(7)

The Lévy stability index is obtained by fitting the ratio to the formula [27]

(8)

which can be simplified to the form

(9)

where. Using the above equations, one gets

(10)

(11)

(12)

Therefore, if one defines

(13)

we get

(14)

when.

On the basis of the above formalism, it has been proposed [17] that the Lévy stability index can be obtained using the following procedure:

Ÿ Find out the value of where. call it B.

Ÿ Fit the part of versus to a straight line and get the slope C.

Ÿ Get the Lévy stability index as

(15)

3. Experimental Details

In the present study, a stack of ILFORD G5 emulsion, exposed to 14.5 A GeV/c ²⁸Si nuclei from the AGS (BNL) has been used. A random sample comprising of 283 interactions with, where represents the number of charged particles produced in an interaction with relative velocity, is analyzed. In order to examine the dependence of various parameters of multiparticle production on beam energy, the data involving 530 interactions, with the same description, produced by 4.5 A GeV/c ²⁸Si nuclei from Synchrophasotron (Dubna), available in our laboratory are also analyzed. Various details, such as scanning procedure, criteria for selecting events and the method of measurements, etc may be found elsewhere [28] [29] . For the classification of the various particles emitted in the various interactions considered for the present study, the usual emulsion terminology [30] has been used. The emitted particles are classified in three categories, black, grey and shower particles, depending upon their limit of ionization and the relative velocity. Black particles refer to the particles with relative velocity. These are mainly target fragments with ionization, where represents the the minimum ionization of a single charged particle. Grey particles exhibit ionization range and their relative velocity is. And the shower particles which consist mainly of relativistic charged particles have the velocity and these are heavily ionizing in nature.

In the present study, we have classified the interactions due to different targets on the basis of the number of heavily ionizing particles produced in an interaction. Heavy particles are defined as the sum of black and grey tracks produced in an interaction i.e.,. The interaction events for which are considered to be the interactions resulting from the CNO target of emulsion whereas, all the interaction events for which are attributed to the interactions due to AgBr target. The phase space variable which has been utilized to characterize the relativistic charged particles in the various interactions is the pseudorapidity variable

with representing the emission angle of the particle with respect to the direction of the pro-

jectile beam.

4. Results and Discussion

4.1. Rényi Dimensions

Variations of the generalized Rényi dimensions, , with the order of the moment, q, for ²⁸Si-Em interactions at the two incident energies are exhibited in Figure 1. For both the energies, satisfies the multifractality condition, namely, for. The generalized Rényi dimensions are found to be positive for all orders of the moment q and demonstrate a decreasing trend with increasing q. The behaviour is in excellent agreement with the predictions of multifractal cascade model [31] . It may be noted that turns out to be

more than unity for, a result in agreement with those reported [32] earlier for different projectiles over a wide range of beam energies. It is also noticed in Figure 1 that the generalized dimensions tend to attain higher values for higher projectile energy in the region characterized by, i.e., for negative order moments. However, in the region having, this trend seems to change, but not very significantly. In order to examine whether there exists any dependence of the Rényi dimensions corresponding to a certain order of moment on the target size, vs q plots for the interactions of ²⁸Si nuclei with CNO and AgBr targets are plotted in Figure 2. The Rényi dimensions have higher values for the interactions due to heavier targets for each order of the moment although the effect appears to be rather more pronounced for the situation corresponding to. One of the reasons for the higher values of the Rényi dimensions for the interactions due to heavier targets may be attributed to increase in the average multiplicity with increasing target mass [33] .

4.2. Multifractal Spectra

Figure 3 shows the variation of the spectral function, , with the Lipschitz-Holder exponents, , for 4.5 A and 14.5 A GeV/c ²⁸Si-Em interactions. The spectra are concave downwards centered around corresponding to and a common tangent at an angle of. This observation agrees fairly well with the predictions of gluon model [15] . However, is not peaked in any of the cases studied which is an indication of non-smooth nature of the multiplicity distribution of the particles produced in the interactions considered in the present study. The left wings of the spectra are sensitive to the peaks whilst the right wings belong to the valleys in their respective pseudorapidity distributions. The spectra at the two energies are nearly similar in the left wings. However, in the right wing corresponding to, the spectrum for the higher energy tends to broaden.

For investigating whether spectra depend on target mass, the spectra for the interactions of ²⁸Si nuclei with CNO and AgBr targets are plotted in Figure 4 for both the energies. It is observed that for the interactions due to AgBr targets the spectra have larger widths in comparison to the spectra for the interactions due to lighter (CNO) targets. It may further be noted that the contribution to the broadening of the width of the spectra with increasing target mass comes mainly from the regions corresponding to. However, all the spectra are wide enough to indicate the occurrence of multifractality for the interactions considered.

4.3. Lévy Stability Index

The variation of with for the interaction of ²⁸Si nuclei with emulsion at 4.5 A and 14.5 A GeV/c are presented in Figure 5. The solid lines in the figures represent linear fittings to the data. Si- milar plots for interactions with CNO and AgBr targets are represented in Figure 6 and Figure 7. The Lévy sta- bility indicies for the various types of interactions evaluated by linear fittings to with plots are given in Table 1. It is clearly evident from the Table that the Lévy stable index for all the interactions studied in the present work lies in the range [0, 2] in consistency with the Lévy stability theory.

5. Conclusion

The multifractal Rényi dimensions for the interactions of 4.5 A and 14.5 A GeV/c ²⁸Si nuclei with CNO and AgBr targets exhibit a behaviour which manifests the multifractal nature of the multiparticle final state in these interactions. The Rényi dimensions are found to obey the basic law of multifractality. Further, the Rényi dimensions exhibit a dependence on the target mass; the values of Rényi dimensions are higher for heavier target mass. The multifractal spectrum is observed to be concave downwards with maximum corresponding to which supports the multifractality in the multiparticle production in the various interactions studied in the present work.

The Lévy stability indicies evaluated from the multifractal spectra for these interactions lie in the range [0, 2] which is in consistency with the Lévy stability theory.

Acknowledgements

The authors are thankful to Professor Nisar A. Rather, Head, Department of Mathematics for his valuable comments during this work.

References