Journal of Modern Physics
Vol.06 No.08(2015), Article ID:58184,7 pages
10.4236/jmp.2015.68112
Bounds on the Number of Light Neutrinos Species,
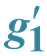 Coupling and Z − Z′ Mixing Angle in a U(1)B−L Model
Coupling and Z − Z′ Mixing Angle in a U(1)B−L Model
A. González-Sánchez1,2, A. Gutiérrez-Rodríguez1*, M. A. Hernández-Ruíz3
1Facultad de Fsica, Universidad Autónoma de Zacatecas, Zacatecas, México
2LERMA, CNRS UMR 8112, Observatoire de Paris, Paris, France
3Facultad de Ciencias Qumicas, Universidad Autónoma de Zacatecas, Zacatecas, México
Email: *alexgu@fisica.uaz.edu.mx
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).


Received 28 March 2015; accepted 19 July 2015; published 22 July 2015

ABSTRACT
The constraints on the number of neutrinos generations,
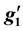 coupling and
coupling and
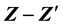 mixing angle through the invisible width method, and in the framework of a
mixing angle through the invisible width method, and in the framework of a
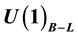 model are obtained. Based on the experimental value reported by the LEP for the rate
model are obtained. Based on the experimental value reported by the LEP for the rate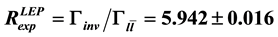 , we obtained a bound on the
, we obtained a bound on the
 coupling,
coupling, . In addition, we derive 90% C.L. bounds on the
. In addition, we derive 90% C.L. bounds on the
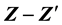 mixing angle
mixing angle , improving the existing bounds by one order of magnitude.
, improving the existing bounds by one order of magnitude.
Keywords:
Ordinary Neutrinos, Neutral Currents, Models beyond the Standard Model

1. Introduction
The number of fermion generations, which is associated to the number of light neutrinos, is one of the most important predictions of the Standard Model of the electroweak interactions (SM) [1] -[3] . In the SM, the decay width of the Z boson into each neutrino family is calculated to be
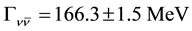 [4] . Additional generations, or other new weakly interacting particles with masses below
[4] . Additional generations, or other new weakly interacting particles with masses below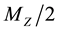 , would lead to a decay width of the Z into invisible channels larger than the SM prediction for three families while a smaller value could be produced, for example, by the presence of one or more right-handed neutrinos mixed with the left-handed ones [5] . Thus the number of light neutrinos generations
, would lead to a decay width of the Z into invisible channels larger than the SM prediction for three families while a smaller value could be produced, for example, by the presence of one or more right-handed neutrinos mixed with the left-handed ones [5] . Thus the number of light neutrinos generations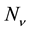 , defined as the ratio between the measured invisible decay width of the Z,
, defined as the ratio between the measured invisible decay width of the Z,
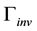 , and the SM expectation
, and the SM expectation
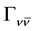 for each neutrino family, needs not be an integer number and has to be measured with the highest possible accuracy.
for each neutrino family, needs not be an integer number and has to be measured with the highest possible accuracy.
The most precise measurement of the number of light
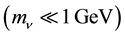 active neutrino types, and therefore the number of associated fermion families, comes from the invisible Z width
active neutrino types, and therefore the number of associated fermion families, comes from the invisible Z width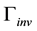 , obtained by subtracting the observed width into quarks and charged leptons from the total width obtained from the lineshape. The number of effective neutrinos
, obtained by subtracting the observed width into quarks and charged leptons from the total width obtained from the lineshape. The number of effective neutrinos


where

In the SM the experimental value from the four LEP experiments for the number of light neutrinos species is

The existence of a heavy neutral






Our aim in this paper is to estimate constraints on the number of neutrinos generations,



This paper is organized as follows. In Section 2, we present the theoretical framework. In Section 3 we present the numerical computation. Finally, we summarize our conclusions in Section 4.
2. Theoretical Framework
We consider a




where





The Lagrangian for the scalar sector of the


where the potential term is [23] ,

with



where the doublet and singlet scalars are

with




From the Lagrangian of the



where the couplings of the



where






3. Results
In order to compare the respective expressions with the experimental result for the number of light neutrinos species

Since Equation (2) reduces the influence of the top quark mass, the expression

order to get information on the meaning of


The definition given in Equation (2) replaces the expression

top quarks mass. To get information on the meaning of



where


with




This new expression is a function of the mixing angle

















In order to estimate a limit for the number of light neutrinos species





In Figure 2, we plot the function (11) in the




is a result of both factors in Equation (11). In this figure


broading. This analysis was done using the experimental value given in Equation (2) for





whose central value is quite close to the standard model of three active neutrinos species.
Figure 1.



Figure 2. Allowed region for




The correlation between the mixing angle






By reversing the process we determined a limit on the








which is consistent with that obtained through from a Renormalisation Group Equation (RGE) analysis [30] - [32] .
Finally, is clear that the effects induced by the tree level






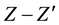




4. Conclusion
From the invisible width method and and in the framework of a











Figure 3. Correlation between


Figure 4. The curve shows the shape for



Figure 5. The curves shows the shape for



Table 1. Bounds on the


Acknowledgments
We acknowledge support from CONACyT, SNI, PROMEP and PIFI (México).
Cite this paper
A.González-Sánchez,A.Gutiérrez-Rodríguez,M. A.Hernández-Ruíz, (2015) Bounds on the Number of Light Neutrinos Species, g'1 Coupling and Z - Z′ Mixing Angle in a U(1)B-L Model. Journal of Modern Physics,06,1077-1084. doi: 10.4236/jmp.2015.68112
References
- 1. Glashow, S.L. (1961) Nuclear Physics, 22, 579-588. http://dx.doi.org/10.1016/0029-5582(61)90469-2
- 2. Weinberg, S. (1967) Physical Review Letters, 19, 1264. http://dx.doi.org/10.1103/PhysRevLett.19.1264
- 3. Salam, A. (1968) In: Svartholm, N., Ed., Elementary Particle Theory, Almquist and Wiskell, Stockholm, 367.
- 4. Olive, K.A., et al. (Particle Data Group) (2014) Chinese Physics C, 38, Article ID: 090001.
http://dx.doi.org/10.1088/1674-1137/38/9/090001 - 5. Jarlskog, C. (1990) Physics Letters B, 241, 579-583. http://dx.doi.org/10.1016/0370-2693(90)91873-A
- 6. Abbaneo, D., et al. (n.d.) (LEP), arXiv: hep-ex/0412015.
- 7. Acciarri, M., et al. (L3 Collaboration) (1994) Z. Phys., C62, 551.
- 8. Buskulic, D., et al. (ALEPH Collaboration) (1994) Z. Phys., C62, 539.
- 9. Barger, V., Kneller, J.P., Lee, H.S., Marfatia, D. and Steigman, G. (2003) Physics Letters B, 566, 8-18.
http://dx.doi.org/10.1016/S0370-2693(03)00800-1 - 10. Hannestad, S. (n.d.) arXiv: astro-ph/0303076.
- 11. Cyburt, R.H., Fields, B.D. and Olive, K.A. (2003) http://arxiv.org/abs/astro-ph/0302431
- 12. Ichikawa, K., Kawasaki, M. and Takahashi, F. (2007) http://arxiv.org/abs/astro-ph/0611784
- 13. Robinett, R.W. (1982) Physical Review D, 26, 2388-2395. http://dx.doi.org/10.1103/PhysRevD.26.2388
- 14. Green, M.B. and Schwarz, J.H. (1984) Physics Letters B, 149, 117-122.
http://dx.doi.org/10.1016/0370-2693(84)91565-X - 15. Mohapatra, R.N. and Pal, P.B. (1991) Massive Neutrinos in Physics and Astrophysics. World Scientific, Singapore. http://dx.doi.org/10.1142/1246
- 16. Senjanovic, G. (1979) Nuclear Physics B, 153, 334-364.
http://dx.doi.org/10.1016/0550-3213(79)90604-7 - 17. Senjanovic, G. and Mohapatra, R.N. (1975) Physical Review D, 12, 1502-1505.
http://dx.doi.org/10.1103/PhysRevD.12.1502 - 18. Baur, U., Schildknecht, D. and Schwarzer, K.H.G. (1987) Physical Review D, 35, 297-304.
http://dx.doi.org/10.1103/PhysRevD.35.297 - 19. Jenkins, E. (1987) Physics Letters B, 192, 219-222. http://dx.doi.org/10.1016/0370-2693(87)91172-5
- 20. Buchmuller, W., Greub, C. and Minkowski, P. (1991) Physics Letters B, 267, 395-399.
http://dx.doi.org/10.1016/0370-2693(91)90952-M - 21. Emam, W. and Khalil, S. (2007) The European Physical Journal C, 52, 625-633.
http://dx.doi.org/10.1140/epjc/s10052-007-0411-7 - 22. Abe, T., American Linear Collider Working Group, et al. (2011) http://arxiv.org/abs/hep-ex/0106057.
- 23. Basso, L., Belyaev, A., Moretti, S., Pruna, G.M. and Shepherd-Themistocleous, C.H. (2011) The European Physical Journal C, 71, 1613. http://dx.doi.org/10.1140/epjc/s10052-011-1613-6
- 24. Ferroglia, A., Lorca, A. and van der Bij, J.J. (2007) Annalen der Physik, 16, 563-578.
http://dx.doi.org/10.1002/andp.200710249 - 25. Rizzo, T.G. (2006) http://arxiv.org/abs/hep-ph/0610104.
- 26. L3 Collaboration, Acciarri, M., et al. (1994) Zeitschrift für Physik C, 62, 551-576.
- 27. Huerta, R., Maya, M. and Miranda, O.G. (1997) Zeitschrift für Physik C Particles and Fields, 73, 701-703.
http://dx.doi.org/10.1007/s002880050362 - 28. Gutiérrez-Rodrguez, A., Hernández-Ruiz, M.A., Pérez, M.A. and Pérez-Vargas, F. (2007)
http://arxiv.org/abs/hep-ph/0702076. - 29. Gutiérrez-Rodrguez, A., Hernández-Ruiz, M.A., Pérez, M.A. and Pérez-Vargas, F. (2009) Modern Physics Letters A, 24, 135-141. http://dx.doi.org/10.1142/S0217732309027431
- 30. Basso, L. (2007) A Minimal Extension of the Standard Model with B.L Gauge Symmetry. Master’s Thesis, Università degli Studi di Padova, Padova. http://www.hep.phys.soton.ac.uk/???l.basso/BL
- 31. Chankowski, P.H., Pokorski, S. and Wagner, J. (2006) The European Physical Journal C, 47, 187-205.
http://dx.doi.org/10.1140/epjc/s2006-02537-3 - 32. del Aguila, F., Coughlan, G.D. and Quiros, M. (1988) Nuclear Physics B, 307, 633-648.
http://dx.doi.org/10.1016/0550-3213(88)90266-0
NOTES
*Corresponding author.








