Received 22 March 2015; accepted 16 May 2015; published 19 May 2015

ABSTRACT

A new alternative approach to the statistical behavior of particle-particle collisions is introduced. The alternative approach is derived rigorously from well known mechanical laws; and the results given by it, quantitatively and qualitatively different from what the standard kinetic theory yields, can be directly checked with computer-simulated or realistic experiments. More importantly, from the introduction of it, a number of new concepts and new methodologies emerge, which might turn out to be very significant to the future development of nonequilibrium statistical mechanics.

Keywords:

Non-Equilibrium, Statistical Mechanics, Boltzmann Equation, Distribution Function, Discontinuity

1. Introduction

It is commonly believed that the statistical behavior of classical particle-particle collisions has been adequately codified into the equations of nonequilibrium gas dynamics (kinetic theory), and there is nothing truly new to today’s physicists. However, as has been pointed out by us [1] [2] , this belief is questionable.

What made us question the validity of the standard theory might be summarized as the following. In the context of gas dynamics, particle-particle collisions are supposed to be examined in the six-dimensional position- velocity phase space, but the space, though superficially simple, is inherently counterintuitive. When a six- dimensional statistical dynamics is of concern, it is often the case that our attention is invited to certain incomplete and misleading pictures. To get a taste of such trickiness, let’s briefly review a long-neglected fact associated with the Boltzmann equation [3] : while the differential operator on its left-hand side enjoys a relatively obvious position-velocity symmetry, the integral operator on its right-hand side does not exhibit any form of position-velocity symmetry. In this regard, one may reasonably wonder: How can the equation’s two sides be always equal when they behave themselves so differently?

In this paper, after advancing several typical examples, an alternative approach is proposed, which takes care of the position space and the velocity space in a relatively balanced way. The proposed formalism is strictly based on well-known mechanical laws, and the results given by it can be directly compared with computer simulations. More importantly, from the introduction of this alternative approach, a number of new concepts and new methodologies emerge, which might turn out to be very significant to the future development of nonequilibrium statistical mechanics.

The structure of this paper is the following. In Section 2, several examples are advanced in which particle- particle collisions cannot be well treated by the standard kinetic theory. In Section 3, an alternative approach is proposed. In Section 4, the newly proposed alternative approach is extended to more general situations. In Section 5, a brief summary is provided.

2. Typical Examples of Particle-Particle Collisions

To investigate the collective behavior of particle-particle collisions, we shall in this paper concern ourselves with three different, but interconnected, situations shown in Figure 1. They are a) a parallel beam of particles scattered by a group of resting particles, b) two parallel beams of particles colliding in the head-on manner, and c) two ordinary gases colliding with each other.

To begin with, let’s first look at the simplest situation illustrated in Figure 1(a). Suppose that the parallel beam on the left side is moving in the 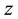-direction (rightwards), and the distribution function of it is

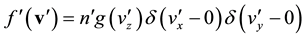(1)

where 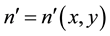is considered to be time-independent and 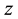-independent and 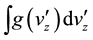over 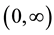is equal to 1. The resting particles on the right side are described by the distribution function

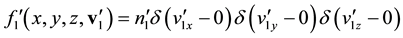(2)

where 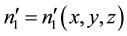is time-independent.

There are several reasons why we start our investigation with this particular example. Firstly, this is the case to which the standard collision theory is presumably applicable. Secondly, this is the case that we, as physicists, can easily realize and easily monitor in computer simulation. Thirdly, this is the case in which the complexity of the subject is largely reduced but the statistical characteristics of the subject remain intact (so the insight gained will be generally instructive).

It is further assumed that a virtual detector, marked as in the figure, is placed at the position where the local distribution function is of interest. This arrangement possesses great importance in this paper; and the basic idea behind it is that the distribution function determines, almost uniquely, the local flux, and hence the distribution function should be directly computable if the flux information gathered by the detector situated there is somehow known. It will be seen that with certain improvement and refinement this simple idea works nicely. In contrast with that, the basic idea of the standard theory seems rather cumbersome. According to the standard theory, to determine the distribution function at a place we are supposed to investigate how the distribution function varies at the place, and to determine how the distribution function varies at the place we are supposed to investigate virtually all the fluxes around the place (eventually 12 coming-or-going fluxes are examined).

Before entering the next section, where a new alternative approach will be introduced, let’s briefly go through what the Boltzmann equation has to say about the situation. Referring to Figure 1(a), suppose that the symmetry axis of is the positive -coordinate axis and the origin of the -coordinate starts from the bottom of the collision region. Thus, the distribution function of the collision-produced particles moving along the 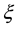-axis obeys (with no external forces)

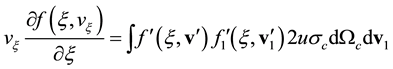, (3)

in which 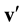and are the initial velocities of two colliding particles while and stand respectively for the final velocities of the two particles, , is the cross section of the scattering and is the solid angle of the scattering. (Notably, and are defined in the so-called center-of-mass frame.) From Equation (3), for a definite can be determined by

. (4)

In writing these two formulas, it is understood that the two initial gases are dilute enough so that the collision probability between and is a first-order quantity and the collision probability between and (or) can be ignored. It is also understood that the relationship between, , and in Equation (3), or (4), obeys the energy-momentum conservation law, which in general consists of four independent equations.

Surprisingly, although formally pertinent, expression (4) yields no meaningful result for the situation. Firstly, if we wish to compute the integral involved, we find no attainable way to get rid of the five -functions in and. Secondly, if we assume that the five -functions disappear simply due to the five-fold velocity integration of Equation (4), the role played by the four equations of the energy-momentum conservation law becomes unknown. Finally, if we somehow managed to make Equation (4) mathematically evaluable, the issue would become even more puzzling in the sense that the result of Equation (4) can be schematically represented by the dotted curve in Figure 2 (reflecting the fact that the integrand of the integral is positive-definite), while our physical and geometrical intuition, as well as a well-performed computer simulation, tells us that the real distribution function varies according to the solid curve given in Figure 2 (the asymptotic behavior of must obey the inverse-square law).

When treating the examples shown in Figure 1(b) and Figure 1(c), similar difficulties will be met with. In particular, the difficulty shown in Figure 2 is always there.

There has been a detailed investigation about the sources of the aforementioned problems [1] . In this paper, we shall focus ourselves on proposing a new alternative approach.

3. An Alternative Approach

In connection with the situation shown in Figure 1(a), we now look at Figure 3(a) and Figure 3(b), in which

the aftermath of a collision is illustrated in the position space and in the velocity space respectively. The two figures are drawn quite generally and their full implications will manifest themselves in this and the next sections.

In Figure 3(a), suppose that is the position of the detector’s inlet, and that the velocities of the particles recorded by the detector fall into a definite speed range and a definite solid angle. Then, the distribution function at the inlet can be roughly expressed as

, (5)

where is the area of the detector’s inlet, is the time interval of recording, is the number of the particles recorded by the detector. Expression (5) can be interpreted as saying that there is a direct connection between the flux detected by the detector and the distribution function of our primary concern. It is this direct connection, though still primitive at this stage, that will guide us to the very end of our investigation.

Concerning expression (5), there are essential things worth discussing. To ensure that the right side of the expression stands for the “exact” distribution function at the position point, the quantities, , and have to be infinitely small. (By the term exact, we mean that the right side of the expression can be qualified as a strict mathematical limit.) However, allowing all these quantities to be simultaneously infinitesimal gives rise to practical problems. For instance, if both and are indeed infinitely small, in expression (5) receives contribution only from the collision region that is limited to a one-dimensional straight line, which is nothing but the very symmetry axis of the detector. Obviously, this type of approach can be accomplished only in mind.

To make expression (5) physically meaningful in rather general situations, we shall adopt the following two assumptions: 1) is very small, infinitesimal in the theoretical sense, and 2) and are finite and definite (still small though). It turns out, to describe force-free Boltzmann gases, accepting these two assumptions is convenient and largely necessary.

Under these two assumptions, we redefine the distribution function as a mathematical hybrid:

, (6)

where with and being respectively the lower and upper bounds of, and includes all the particles recorded during whose velocities fall in and. Namely, this distribution function is a mathematical limit in the position space, but a mathematical average in the velocity space, averaged over the finite volume element.

At this point, one remark seems in order. In the standard theory the distribution function, as the primary concept of the theory, is often defined or interpreted in intentionally vague language. For instance, in one of the books on nonequilibrium statistical mechanics [4] it is stated that the distribution function, denoted as therein, is the ratio in which and are supposedly “large enough to contain a lot of particles, but small compared to the range of variation of. Then, an interesting question about expression (6) arises. Why does the approach herein define the distribution function in such clear and strict mathematical terms? To this question, the answer given by us is simply the following: to compute a distribution function certain limiting processes need to be invoked; but if there is not an adequate set of mathematically well-defined quantities those limiting processes may lose their validity explicitly or implicitly.

We take three steps to compute expression (6): 1) finding out the position region in which particle-particle collisions may possibly give contribution to; 2) formulating the collision number in this position region; and 3) investigating how collision-produced particles spread in the position space and in the velocity space, and then determining in what portion those collision-produced particles will indeed be recorded by the detector.

The first two steps can be accomplished rather easily. Since the solid angle has been assumed to be definite and finite and the inlet area has been assumed to be very small (infinitesimal), we find the trajectory cone denoted by in Figure 3(a) to be the position region in which collisions may directly give contributions to. In this particular sense, the cone will be named as the upstream path zone, or up-zone for short. The number of the collisions taking place inside the up-zone can be expressed by

(7)

where stands for an infinitesimal region in. Inserting Equations (1) and (2) into Equation (7), we obtain

. (8)

To accomplish the third step aforementioned, let’s first note that the information concerning how the scattered particles spread in the position space and the velocity space is stored in. Since is conveniently defined in the center-of-mass frame, and the position and velocity spaces we care about are defined in the laboratory frame, an extra examination is needed.

Referring to Figure 3(a) and Figure 4(a), we find that there is an infinitely sharp cone formed by the point, as the apex, and the area element, as the base. So, the solid angle bounded by the cone, , is equal to

. (9)

Since is infinitely small, is infinitely small to. Thus, if a particle can enter the detector from the up-zone, the particle’s velocity will definitely falls in. Namely, from now on, the only thing we need to make sure is that the collision-scattered particles emerge within and in the laboratory frame.

To connect the center-of-mass frame and the laboratory frame, we have to deal with the energy-momentum

conservation law explicitly. Let all the particles in our consideration have the same mass (for simplicity); and let and be the initial velocities of two colliding particles and and be the final velocities of the two particles respectively. The energy-momentum conservation law then takes the form

, (10)

where

(11)

The above expressions show that for a pair of and, the final velocities and have only two degrees of freedom, distributing on an infinitely thin energy-momentum (EM) membrane in the velocity space, as has already been illustrated in Figure 3(b). Referring to Figure 3(b) and Figure 4(a) simultaneously, we find out that in the velocity space, for the fixed,

, (12)

in which and (in this section). This relationship defines the patch of the EM membrane on that the scattered particles will indeed be recorded by the detector. Finally, by virtue of Figure 4(b), we have

. (13)

With help of Equations (8), (9), (12) and (13), the limit-average-hybrid distribution function defined by Equation (6) is

, (14)

in which the integration region of is over the up-zone, the integration range of is in which is the angle between and the z-axis, and is the function of. In this formula only the particles coming from are taken into account.

Unlike expression (4), expression (14) is obviously computable. It yields a finite and definite result no matter whether is inside or outside the collision region. When is located at a place remote to the collision region (which defines the asymptotic behavior of the particle-particle collisions), in Equation (14) obeys the inverse-square relationship, thus ensuring the conservation of particle number globally.

4. Extensions of the Alternative Approach

Now, we look at how to extend our proposed approach to the cases shown in Figure 1(b) and Figure 1(c).

Let the gas on the left-hand side of Figure 1(b) be represented by

(15)

where is time- and -independent and over is equal to 1; let the gas on the right- hand side of Figure 1(b) be represented by

, (16)

where is also time- and -independent and over is equal to 1.

Again, we are interested in determining defined by Equation (6), where stands for the

position of the detector’s inlet in Figure 1(b).

By defining the up-zone, , around the symmetry axis of the detector, we know that the collision number taking place in the zone can still be expressed by Equation (7). So, the collision-produced particles that can enter the detector are

, (17)

in which is limited to the patch on that the scattered particles will move almost exactly toward the detector in the laboratory frame.

Now, the energy-momentum conservation law shows us that

. (18)

and Equation (17) becomes

, (19)

in which

(20)

is the Jacobian of the variable transformation. Notice that Figure 4(a) makes sense generally as long as we disregard in it. (Obviously, holds only for the case discussed in the last section.) It is then obvious that Equation (9) still holds. Furthermore, for the fixed in that figure, we have

, (21)

where is the infinitesimal volume element into which the particles recorded by the detector are supposed to fall. Eventually, with help of Equations (9), (19) and (21) the distribution function defined by Equation (6) becomes

, (22)

in which the integration region of covers the up-zone, the integration range of is from to and is the function of. Other quantities should be determined with care, and the following diagram may provide an additional help

(23)

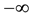
namely, by and we obtain, by geometrically subtracting from we get, with help of the function and can be determined.

As for the general case shown in Figure 1(c), the formulation is about the same. Firstly, the collision number taking place in the up-zone can be represented by

. (24)

where and are the distribution function at the collision position and at the collision time. By invoking the variable transformation defined by Equation (11), we arrive at

, (25)

in which

. (26)

Notice that in Equation (25) can be replaced by where stands for the direction of. Also notice that Equations (9) and (21) hold significance in this general situation. Eventually, we find that the distribution function defined by Equation (6), at a particular time, is

, (27)

in which, is over the upstream path zone, is over, is over the entire

velocity space, is over, and is the function of. Other quantities in this expres-

sion can be determined by

(28)

which is interpreted similarly to the diagram given in expression (23).

Obviously, both expressions (22) and (27) are directly computable, and ready to be checked with computer-simulated or realistic experiments.

It is easy to see that if in the formulas of this paper is allowed to approach zero, the whole formalism makes no sense, which again says that the “exact” distribution function is inherently indeterminable. More than that, this formalism has actually shown that, if we are a weightless and infinitely small observer moving together with a group of collision-produced particles, the distribution function observed by us is, in general, not path- invariant, which in turn challenges the long-held tacit assumption that any distribution function, produced by whatever mechanisms, is a continuous one or can be treated as a continuous one.

5. Summary

In this paper, to formulate the statistical behavior of particle-particle collisions, a new alternative integral formalism has been introduced. The results given by the new formalism are quantitatively and qualitatively different from what the standard theory yields. If interested, readers may confirm or deny them by applying their own theoretical and/or numerical approaches.

More importantly, along with the introduction of the new approach, a set of new concepts and methodologies are proposed, which might turn out to be very significant to the future development of nonequilibrium statistical mechanics. Some of them are:

Ÿ Due to the discontinuity concern, the distribution function in a nonequilibrium approach should be defined as an average in the position-velocity phase space, at least partially.

Ÿ Instead of using differential-integral equations, approaches of completely integral type should be employed.

Ÿ Instead of examining the events in a control volume element, what takes place in an upstream path zone should be investigated.

Ÿ Collisional effects should be studied in both the position space and the velocity space. The energy- momentum conservation law should be fully incorporated.

Acknowledgements

The author is grateful to Drs. M. Berry, O. Penrose, R. Littlejohn, V. Travkin, W. Hoover, Hanying Guo, Tian- rong Zhang, Keying Guan, Xingren Ying for their direct or indirect encouragement. The discussions with them have been pleasant and helpful.

References