Received 3 March 2015; accepted 17 March 2015; published 19 March 2015

ABSTRACT

This paper is addressed to the problem of Galilei invariant basis construction for identical fermions systems. The recently introduced method for spurious state elimination from expansions in harmonic oscillator basis [1] is adopted and applied to bound states of two particles system with Coulomb potential description. Traditional expansions in this case demonstrate the extremely well-known slow convergence, and hence this is the best problem with known exact solutions for the test of the method. Obtained results demonstrate the significant simplification of the problem and fast convergence of expansions. We show that the application of this general method is very efficient in a test case of the energy spectrum calculation problem of two particles with different masses interacting with Coulomb potential.

Keywords:

Harmonic Oscillator Basis, Spurious States, Variational Method, Quantum Systems with Coulomb Potential

1. Introduction

The recent development of parallel-computing facilities has promoted a rapid evolution of the large-scale quantum systems’ calculations. Therefore, there is a chance to check the precision of well-known methods for these systems’ description, as a rule, violating principle of Galilei invariance.

Matter is invariant with respect to translations in space; therefore, the operators of observables and wave- functions of the self-bound system must be translationally invariant. However, this invariance significantly complicates the problem. As a result, the best-known methods for the quantum systems’ description, such as the Shell Model or the Hartree-Fock Self-Consistent Field Method [2] , produce wave-functions, dependent on a set of one-particle radius-vectors, and thus also on the center-of-mass radius-vector of the system. This shortage of mentioned methods is well-known; however, these wave-functions are very attractive because they allow a simple procedure of identical fermions, composing these systems or their subsystems, antisymmetrization. In some cases, such as solid state, where the ion jelly is much heavier than the electrons, this approximation is very good. However, in an atom or molecule due to electrons and nuclei masses ratio, approximately equal to 10⁻⁴, applying the wave-functions dependent on redundant (i.e. center-of-mass of entire system) variable, one cannot be sure about the declared high precision of calculations. Obviously, for nuclei and hadrons the translational invariance appears as an even more significant problem. Common is the statement claiming that the error in this case will be of order 1/A, where A is baryon charge of corresponding nucleus. Obviously, now such precision of atomic nuclei description is unacceptable.

Some methods, developed for few-body systems, are designed to produce translationally invariant wave functions. These are methods based on the Faddeev [3] , Faddeev-Jakubovsky [4] , and functional-differential equations [5] or on the expansions in a large basis of harmonic oscillator functions [6] - [11] . In these approaches the translational invariance of wave function arises from equations written in intrinsic (Jacobi) variables. However, an attempt to apply these methods in order to calculate the atomic nuclei has shown [12] that modern computers are not yet able to solve the problem for systems with larger particle number. Therefore, at the moment there are no possibilities to significantly improve or simplify this formalism. Thus, Galilei invariant basis construction for identical fermions system in straightforward way is a very complex problem.

Therefore, the basis of wave functions written in one-particle degrees off reedom is the best solution for quantum systems, composed of identical fermions, description. The well-known and traditional solution of this problem is Shell Model (SM), based on the fact that wave function is written as a product of one particle functions, antisymmetrized applying fractional parentage coefficients [13] [14] and equipped by quantum numbers that characterize this state. The only problem of SM is violation of translational invariance. Different procedures of projection restoring translational invariance of such function after Schrödinger equation solution are described as in literature [15] - [18] . However, the success of these operations is very problematic. First of all, intrinsic wave function cannot be characterized by any configuration. As it is shown in [1] , the commutator of particle’s angular momentum operator and total momentum of intrinsic wave function operator, excluding a few trivial cases, does not equal zero, and hence wave function with defined one-particle states cannot appear as structural element of intrinsic wave function. Moreover, arbitrary linear combination of Shell Model wave functions is dependent on center-of-mass radius-vector; hence, intrinsic wave function cannot be expressed in this way.

The only choice for the solution of this problem is center of mass state fixation. The center-of-mass Hamiltonian and intrinsic Hamiltonian operators commute, because they are functions of different variables, hence center-of-mass Hamiltonian commutes also with total Hamiltonian, expressed in one-particle variables and both have coinciding sets of eigen functions. The wave function of bound state has to be square integrable, hence square integrable has to also be the center-of-mass wave function. The easiest way for such function constructionis modification of Hamiltonian adding and subtracting some potential, dependent on center-of-mass radius vector. The best choice for this operator is harmonic oscillator potential because this operator, proportional the square of center-of-mass radius vector can be easily transformed to form of operator, dependent on one-particle radius- vectors, as defined in [1] .

Therefore, for Galilei invariant quantum system description one needs the following operations. The first one is the construction of harmonic oscillator shell model functions basis, antisymmetrized in respect of identical fermions, composing system under investigation or it’s subsystem degrees of freedom permutations and equipped by necessary quantum numbers like total number of oscillator quanta, total momentum, parity and so on. Later on, linear combinations of these functions, corresponding the ground state of mentioned above three dimensional center of mass harmonic oscillator Hamiltonian are necessary. As is shown in [1] , this operation in finite subspaces, corresponding given number of total oscillator quanta produces one basic function. This basis, applied for Hamiltonian matrix diagonalization, significantly reduces dimension of corresponding matrix. Finally, the wave function of quantum system, dependent on one particle variables, having compact and usual form, applied for mean values of operators, corresponding system observables, gives results, coinciding with ones, obtainable after Galilei invariant wave function application, because all operators of observables are translationally invariant, i.e. independent on center-of-mass radius-vector.

The standard procedure, applying for quantum system wave function expansion the basis of many particle harmonic oscillator functions, cannot ensure Galilei invariant results of calculations because the basis without mentioned modification contains significant amount of basic functions with excited center of mass, called as spurious states. Well known in such approaches are huge matrices of Hamiltonian and bad convergence of expansions, first of all -due to Gaussian asymptotic of harmonic oscillator functions.

The reduction of basis dimensions after operation, as it follows from [1] and the results presented below, is rather impressive. After the mentioned projection into the non-excited centre-of-mass subspaces, satisfying fixed total oscillator quantum number value, the obtained Hamiltonian matrix reduction allows the successful and easy, i.e. applying traditional method, construction of system wave functions. This basis is very convenient, as onlyin it Talmi transformations [19] [20] allow significant simplification of two or larger number of particles operator’s matrix elements calculations.

The purpose of this paper is to describe and illustrate the application of this method for handling the energy spectrum calculation problem of two particles with different masses interacting with Coulomb potential. Since the treatment of Coulomb potential in the harmonic oscillator basis is known as a hard computational problem, the obtained in this case peculiarities of the method will be valuable for further investigations of many-particle systems.

2. Two Particles System

The Hamiltonian of two particles system, with masses 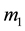and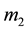, and charges equal and interacting with Coulomb potential in laboratory reference frame can be written as sum of single-particle and two particle operators

(2.1)

where 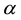is fine structure constant, and 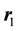the i-th particle radius vector. Let us introduce the more suitable dimensionless coordinates

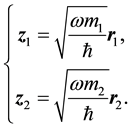(2.2)

Here 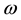is a parameter with dimension of angular frequency. Rewriting Equation (2.1) in terms of dimensionless quantities, one obtains

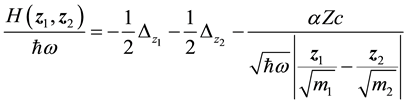(2.3)

The problem under consideration is investigation of spectrum and eigenfunctions of this Hamiltonian expansion in basis of three-dimensional harmonic oscillator functions. The bound angular moment a two-particle har- monic oscillator functions can be expressed in terms of single-particle functions utilizing the angular momentum Clebsch-Gordan coefficients

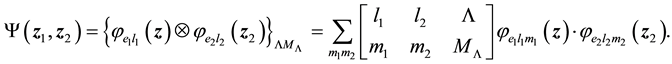(2.4)

Here 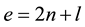is the number of harmonic oscillator quanta, is the principal oscillator quantum number, 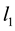, 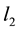are orbital angular moment a and 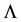is total angular momentum quantum numbers, and are the magnetic quantum numbers of orbital and total angular momentum. Vector coupling of angular momenta is denoted by. The orthogonal and normalized radial harmonic-oscillator wave functions in dimensionless coordinates have the form

(2.5)

where is the Laguerre polynomial, and is the gamma function [21] .

The expectation values of kinetic energy operators of Hamiltonian (2.3) after application of the Wigner-Eckart theorem, may be expressed by reduced matrix element

(2.6)

represented as double-bar matrix element. The reduced matrix element of operator acting only on coordinates of first particle may be expressed in terms of 6j coefficient and the reduced matrix element between the single-particle functions depending only on coordinates of the first particle [22]

(2.7)

Since the considered Hamiltonian is a scalar in angular-momentum space, the tensorial rank of the kinetic energy operator is zero. After application of Equation (2.7), the expression of the reduced matrix element of the first kinetic energy term takes the form

(2.8)

Due to zero value of one of the parameters of the 6j coefficient, it may be significantly simplified [23]

(2.9)

Therefore, the reduced matrix element of the first kinetic energy term may be written as

(2.10)

After these manipulations the matrix element assumes the form

(2.11)

Here we present its abbreviated form as well. The second kinetic energy term of Hamiltonian (2.3) may be evaluated using the formula that expresses the reduced matrix element of operator acting only on coordinates of second particle of the two-particle coupled state in terms of 6j coefficient and the reduced matrix element between the single-particle functions depending only on coordinates of second particle [22]

(2.12)

Then for the matrix element of the second kinetic energy term, between the coupled two-particle harmonic oscillator functions, we find that

(2.13)

The expectation value of the two-particle Coulomb operator from Equation (2.1) can be obtained by expressing them in a single-particle form. This may be accomplished by means of Jacobi coordinates. The orthogonal transformation to the Jacobi coordinates is

(2.14)

at

(2.15)

In these new coordinates the Coulomb potential takes a single-particle form due to relation

(2.16)

where the reduced mass is introduced

(2.17)

The same transformation to Jacobi coordinates should be accomplished for the wave functions. By means of Talmi-Moshinsky brackets the two particle harmonic oscillator functions may be expanded in terms of vector coupled products of the single Jacobi variable functions [20]

(2.18)

Here ε₀ and are oscillator quanta and angular momentum quantum numbers, associated with the center-of- mass motion, and are corresponding quantum numbers of relative motion. The Jacobi coordinate with the zero index is proportional to the center-of-mass coordinate, and Jacobi coordinate with the index equal to one is proportional to their relative coordinate. Thus for the two-particle term of Hamiltonian (2.3) one obtains

(2.19)

The matrix element in Equation (2.19) may be simplified similarly as the kinetic energy terms

(2.20)

Here the integral may be obtained most easily by direct numerical integration. Finally, the matrix element of the first Coulomb term between the coupled two-particle harmonic oscillator functions takes the form

(2.21)

Here, the summation parameters are under restrictions:, , , and. Let us express the matrix elements of Hamiltonian (2.3) in the units of the first eigenvalue of the system of two particles interacting with Coulomb potential. The well-known result in relative coordinates is

(2.22)

The obtained abbreviated form for the Hamiltonian matrix element becomes

(2.23)

Here the dimensionless harmonic oscillator length parameter:

(2.24)

Let us use the formation of the matrix (2.23), its diagonalization, and calculation of the eigenvalues for the Hamiltonian (2.3) as a benchmark. In this case the calculated eigenvalues can be compared directly with well- known spectrum:. The masses of particles are taken as that for proton and electron. However, we would like to point out that the eigenvalues spectrum calculated in the units of the eigenvalue does not depend on the actual masses of the interacting particles.

The dependence of the first five eigenvalues on the dimensionless harmonic oscillator length parameter is displayed in Figure 1. The curves are formed by straight-line segments joining the calculated results. The displayed points are positioned at the values of the varying parameter minimizing the corresponding eigenvalues. Every curve is labeled by their eigenvalue number. The model space is characterized by the total energy oscillator quanta (i.e. the one-particle quantum numbers are under restriction:

). We see that the obtained eigenvalues certainly do not follow the law and spectrum calculated without the projection of the centrum-of-mass is contaminated with nonphysical eigenvalues. Figure 1 shows that every eigenvalue may be minimized at different value of the parameter, at the same time the other eigenvalues will be shifted upwards from their minimal values. It is found that value of the parameter increases for higher eigenvalues. This phenomenon is related to the increase of the spatial extension of harmonic oscillator basis functions with increase of the parameter. Since, the spatial extension of higher eigenfunctions increase as well, the harmonic oscillator basis functions with larger values of parameter is more suitable for their expansion. We should also note that with increasing value of the parameter the number of negative eigenvalues in the calculated spectrum increases rapidly. Indeed, the harmonic oscillator ba-

sis functions with larger values of approximate higher parts of the spectrum. Higher parts of the spectrum contain significantly larger number of eigenstates (e.g. in Hydrogen) and are extremely contaminated with spurious states when calculated in the single particle basis. So, with increasing value of the parameter, the problem becomes more suited for calculation of the higher parts of the spectrum and for this reason we observe the rapid increase of the number of negative eigenvalues for diagonalized Hamiltonian matrices.

The dependence of the ground-state eigenvalue of the Hamiltonian on the size of the basis and the parameter chosen to minimize the ground-state eigenvalue is presented in Table 1. The dimensions of the diagonalized Hamiltonian matrices are presented as well. In general, we observe an overall improvement in the ground- state eigenvalue calculation results with the enlargement of the model space. The obtained results are in line with the well-known fact that the convergence of straight forward variational eigenvalue calculations of many- particle systems with Coulomb interaction in the harmonic oscillator basis is very slow.

3. Spurious States Elimination

For calculation of eigenvalues and eigenfunctions of the two particles with different masses bound by Coulomb potential, we apply the efficient method proposed in [1] . Following this method, at first the projection of eigenfunctions basis to the subspace of non-excited center-of-mass should be performed. In case of the two-particle system, the modified basis, where center-of-mass excitations have been removed before Hamiltonian matrix diagonalization, may be constructed by means of Talmi-Moshinsky brackets:

(2.25)

Here the orthogonal transformation (2.14) to the Jacobi coordinates is applied. The obtained result illustrates the most distinct advantage of the method, i.e. the significant reduction and simplification of modified basis. It should be stressed that unlike the two-particle basis case, the modified basis is strictly decomposed in products of the center-of-mass and relative coordinates terms. So, the spurious states in the modified basis are explicitly separated. The Hamiltonian in the introduced Jacobi coordinates takes the form

(2.26)

Following the method [1] the kinetic energy term depending on the Jacobi coordinate with the zero index which is proportional to the center-of-mass coordinate of two particles should be eliminated. Finally, the Hamiltonian, applying the modified basis without center-of-mass excitations, simplifies and takes the form

(2.27)

Now, it is obvious that due to the applied method the significant simplification of the initial problem is obtained. The problem is reduced to the problem of motion of one particle in the potential with fixed coordinates. The matrix elements of the second kinetic energy term may be easily evaluated

(2.28)

Here we introduce more compact notation for the matrix element of the kinetic energy term depending on the Jacobi coordinate with the index equal to one. The radial harmonic-oscillator wave functions of the form (2.5) may be used for numerical evaluation of the Coulomb matrix elements

(2.29)

Here the more compact notation of Coulomb matrix elements is introduced as well. It should be noted that Coulomb matrix elements may be evaluated analytically in terms of the hypergeometricfunction, which is computationally more efficient especially in the case of large values of quantum numbers

(2.30)

Here widely accepted notations [4] are introduced:

(2.31)

and

(2.32)

The resulting abbreviated form for the Hamiltonian matrix element in the units of the first eigenvalue (2.22) becomes

(2.33)

Let us illustrate the accuracy of calculations by computing the eigenvalues of Hamiltonian (2.30) in the basis of functions (2.25). In Table 2, we present the dependence of the calculated eigenvalues on the parameter chosen to minimize one of the eigenvalues in the obtained spectrum. For example, the first row displays the spectrum obtained when only the first eigenvalue is minimized and the value of parameter for which this eigenvalue is obtained; the second row displays the spectrum, which is calculated with the value of parameter for which the second eigenvalue is minimized, and so on. For comparison, the exact eigenvalues and the differences between exact and calculated eigenvalues are presented as well. We see the same tendencies in dependency of calculated eigenvalueson the value of the parameter as for Hamiltonian (2.23), at the same time the spectrum obtained with Hamiltonian (2.30) is completely free from spurious states.We shall note that in modified basis the dimensions of Hamiltonian matrices are significantly smaller than in the case of two-particle basis. For example, the test case presented in the Table 2 is characterized with maximum value of the principal oscillator quantum number and hence the total energy oscillator quanta. In the two- particle basis dimension of the Hamiltonian matrix constructed for this value of the total energy oscillator quanta will be equal to 2997411, instead of dimension of the Hamiltonian matrix equal to 260 in the modified basis.

4. Conclusions

The purpose of the present work is to demonstrate the efficiency of the spurious state elimination method [1] in case of the two-particle problem and to emphasize the necessity of spurious states elimination vital to the translationally invariant physics of quantum many-particle systems’ calculations. Our overall conclusion is that it is impossible to calculate in single particle basis the spectrum of many-particle system without the separation of spurious center-of-mass solutions except the ground state. That is also impossible in the case of problem with known exact spectrum, since the inherent discrepancy of the exact and calculated spectra is impossible to establish the unambiguous correspondence between the exact and calculated energy levels from calculated spectrum as a function of the dimensionless harmonic oscillator length parameter. Even worse, with increasing the value of parameter, the number of energy levels in the calculated spectrum and the number of candidates to non-spurious states grow rapidly.

The attempt to solve the eigenvalue problem for deuteron in the single particle basis variationally for up to 20 harmonic oscillator quanta using the standard Lawson method [23] for center-of-mass factorization was applied in [24] . Compared with the standard approach, the method applied in this paper has an advantage in producing the significant reduction of the dimension of Hamiltonian matrix due to the preliminary spurious state elimination from expansions. In considered case of the two-particle system, this method simplifies the problem of the interaction between two particles and the relative coordinate case. This leads to a substantial simplification of the calculations. The calculated spectrum of the reduced problem is completely free from spurious states and is computed to high precision. As an example of the relative coordinate problem, the variational method was applied for investigation of Stark effect in neutral hydrogen using a basis set of Laguerre-mesh polynomials of degree 30 [25] . The performed examination of the method [1] shows its good perspectives for calculation of many- particle quantum systems.

Cite this paper

AlgirdasDeveikis,Gintautas P.Kamuntavičius， (2015) New Possibilities of Harmonic Oscillator Basis Application for Quantum System Description. Two Particles with Coulomb Interaction。 Journal of Modern Physics，06，403-413. doi: 10.4236/jmp.2015.64044

References