Journal of Modern Physics
Vol.06 No.01(2015), Article ID:53438,11 pages
10.4236/jmp.2015.61007
An Approach to Plasma Wake Studying
Gennadii V. Gembarzhevskii
Russian Academy of Sciences, The Institute for Problems in Mechanics, Moscow, Russia
Email: gvgemb@ipmnet.ru
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 30 October 2014; accepted 11 November 2014; published 22 November 2014
ABSTRACT
The influence of a glow electrical discharge on the wake behind two cylinders was studied. This effect consists in a redistribution of the power in the velocity pulsation spectrum due to the discharge action on fluid flow. To treat this observation, we need a simple model of intermittent turbulent wake in the vicinity of cylinders. A variant of such model has been developed in the form of two coupled van-der-Pole oscillators representing two interacting von Karman vortex streets behind the cylinders. According to the model, the set of the global wake modes and its concurrence are discussed. Accordingly, a mechanism of the glow discharge effect on the cylinders wake has been proposed.
Keywords:
Turbulentplasma Wake, Alternation, Over-Heating Instability, Reduced-Order Model, Van-der-Pole Oscillators, Vortex Streets Synchronization

1. Introduction
During last century the wake behind cylinders attracted considerable attention and now the research for that is in progress. Such contemporary investigations are of various types, namely, of experimental, numerical, theoretical, and complex ones [1] -[9] . Some recent topic is a flow control over moving body for various aims, such as a delay of laminar regime, or triggering flow separation, heat- and mass-flux modification, etc. Among various types of appropriate actuator for flow control an electrical ones have sufficient advantages, such as the fast response, reliability, low cost [10] [11] . Accordingly, dielectric barrier and corona discharges were intensively studied for such purposes. Among many of them, few examples of flow modification by means of plasma actuators around bluff (cylinders) and smooth bodies (wings) were described in references [12] - [15] .
The problem of our direct interest is in the field of plasma wakes, more exactly, turbulent flows in electrical constant power industrial lasers of kW class, some relevant references to this topic are in papers [16] - [19] . We tried to adopt the technique of flow control by the electrical discharge in the fast-flow CO2-laser where the glow discharge exists ab initio. A promising result has been achieved for this case [20] . In that study the wake from two parallel circular cylinders in the side-by-side arrangement was studied for the mixture composed of 16 Torr nitrogen and 2 Torr helium, see Figure 1. The cross section of the discharge chamber was of 55 ´ 940 mm, the diameter of the quartz cylinders was of 15 mm while the diameter of the copper water-cooled cathode was of 4 mm. The cylinders touched the cathode. This cylinders wake may be treated as a incompressible turbulent flow since the value of the flow Mach number was of  and the value of Reynolds number defined in terms of cylinder diameter
and the value of Reynolds number defined in terms of cylinder diameter  and non-perturb velocity was Re ~ 1000. Mean velocity was measured by means of Prandtl tube. One-point spectra of the wake velocity were measured in 120 mm beneath the axis of one cylinder by means of a transducer of Siddon-Ribner type [21] . Its signal was processed by a PALSE 3560C complex of Bruel & Kjar. Experimental velocity spectra for the wake at non-self-sustained glow discharge and appropriate spectra for the neutral gas flow (that is a reference data) were compared. When the distance between cylinder axes was about
and non-perturb velocity was Re ~ 1000. Mean velocity was measured by means of Prandtl tube. One-point spectra of the wake velocity were measured in 120 mm beneath the axis of one cylinder by means of a transducer of Siddon-Ribner type [21] . Its signal was processed by a PALSE 3560C complex of Bruel & Kjar. Experimental velocity spectra for the wake at non-self-sustained glow discharge and appropriate spectra for the neutral gas flow (that is a reference data) were compared. When the distance between cylinder axes was about 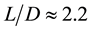 as is in Figure 2, the velocity spectrum with one peak was observed in the case of gas wake. This result was treated as a manifestation of the presence of one global hydrodynamic mode existing in the case of gas wake with above mentioned parameters. On the contrary, for a relevant plasma wake flow the two-peak velocity spectrum was observed and interpreted as a property of intermittent flow of two concurrent global modes. One of global modes of the plasma wake was the same as for neutral gas flow (since its oscillation frequency was the same), whereas another new mode had lower frequency as compared to previous one. When current density at cathode tube was of about
as is in Figure 2, the velocity spectrum with one peak was observed in the case of gas wake. This result was treated as a manifestation of the presence of one global hydrodynamic mode existing in the case of gas wake with above mentioned parameters. On the contrary, for a relevant plasma wake flow the two-peak velocity spectrum was observed and interpreted as a property of intermittent flow of two concurrent global modes. One of global modes of the plasma wake was the same as for neutral gas flow (since its oscillation frequency was the same), whereas another new mode had lower frequency as compared to previous one. When current density at cathode tube was of about 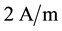 (the case in Figure 2(b)) the dominant part of the energy of coherent oscillations was concentrated in the lower frequency peak. Consequently, this discharge influence appeared to be strong.
(the case in Figure 2(b)) the dominant part of the energy of coherent oscillations was concentrated in the lower frequency peak. Consequently, this discharge influence appeared to be strong.
2. Model of the Wake behind Two Cylinders
For treatment of the discharge effect one has to use some model of the wake. Moreover, when the flow visualization is difficult as it is in our case, even spectral peak classification (of one-point velocity record) requires for some model of the wake. Accordingly our first purpose was developing wake model, no matter appreciable for neutral gas wakes only, but with wide applicability area in Reynolds number variation and in the cylinder spacing alternation. Desirable model has to be the most simple yet leaves room for further extension to such factors as electric discharge influence. Simple wake models are reduced-order models of Landau type, for example [22] . This model is well-studied and justified for low value of supercriticality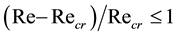 ,
, . In Russia Prof. P. Landa develops similar reduced-order oscillatory models for various physical systems including wakes (with Prof. A. Ginevsky) as well [23] . We used such approach for turbulent wake modeling with van-der- Pole equation as the starting point, accordingly, no immediate limitation on Reynolds number arises for this option. In experiment [20] in the chamber of fast-flow CO2-laser the cylinders of low aspect ratio were used:
. In Russia Prof. P. Landa develops similar reduced-order oscillatory models for various physical systems including wakes (with Prof. A. Ginevsky) as well [23] . We used such approach for turbulent wake modeling with van-der- Pole equation as the starting point, accordingly, no immediate limitation on Reynolds number arises for this option. In experiment [20] in the chamber of fast-flow CO2-laser the cylinders of low aspect ratio were used: . This circumstance allows us neglect the wake dynamics in direction of cylinders axes, according to results [24] . On the author hand, it is desirable to have model appreciable for wide range of interaction intensity of von Karman streets. Then the developed model of the wake from two cylinders with side-by-side arrangement is a set of two dimensionless differential equations for coupled van-der-Pole oscillators representing two interfering Benard-von Karman streets behind cylinders in proximity (how the streets were worked out by the end of the formation zone):
. This circumstance allows us neglect the wake dynamics in direction of cylinders axes, according to results [24] . On the author hand, it is desirable to have model appreciable for wide range of interaction intensity of von Karman streets. Then the developed model of the wake from two cylinders with side-by-side arrangement is a set of two dimensionless differential equations for coupled van-der-Pole oscillators representing two interfering Benard-von Karman streets behind cylinders in proximity (how the streets were worked out by the end of the formation zone):
Figure 1. Scheme of the wake flow in the discharge chamber.
Figure 2. Spectra of the wake velocity pulsations (arbitrary units): for neutral gas flow (a), and for discharge plasma wake (b).
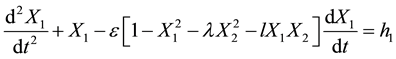 (1)
(1)
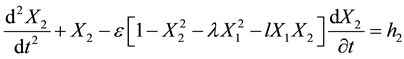 (2)
(2)
Here the oscillator coordinates 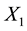 and
and 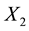 represent the transversal components of the flow velocity in two von Karman streets behind two cylinders respectively. Right-hand sides of the equations describe random forces executed on the zone of street formation by the turbulence of incoming flow. Equation set (1, 2) has three dimensionless parameters. Precisely,
represent the transversal components of the flow velocity in two von Karman streets behind two cylinders respectively. Right-hand sides of the equations describe random forces executed on the zone of street formation by the turbulence of incoming flow. Equation set (1, 2) has three dimensionless parameters. Precisely, 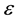 is the native nonlinearity parameter of the partial van-der-Pole oscillator-street,
is the native nonlinearity parameter of the partial van-der-Pole oscillator-street,  and
and 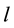 are two parameters of the oscillators cross damping. Here, the peculiarity of this model should be underlined. In an attempt to extend the applicability area of the model, the oscillators coupling form was made nonlinear, accordingly, the term in brackets in set (1, 2) is a square polynomial of general form. Assuming quasi-stationary state of the wake behind the formation zone, the model transforms to a one-dimensional type through the transformation
are two parameters of the oscillators cross damping. Here, the peculiarity of this model should be underlined. In an attempt to extend the applicability area of the model, the oscillators coupling form was made nonlinear, accordingly, the term in brackets in set (1, 2) is a square polynomial of general form. Assuming quasi-stationary state of the wake behind the formation zone, the model transforms to a one-dimensional type through the transformation 



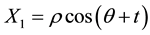

Here 



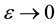



Here, it was introduced the phase difference 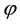

Equations set (5-7) for the case of zero right-hand sides 


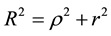
Accordingly, the model of the wake behind the cylinders pair in the side-by-side arrangement takes the final form:



One can see that the developed model (Equations (12-14)) turns out to be relatively simple. Actually, small nonlinearity parameter 
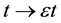



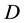
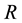

i) Asymmetric mode “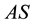
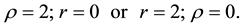
The domain of existence of 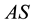

ii) The second one is symmetric mode “

The domain of existence of 

iii) Symmetric mode “

The existence domain of this mode is as follows:
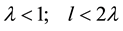
iv) Symmetric mode “
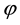
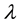

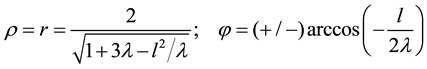
The global mode 
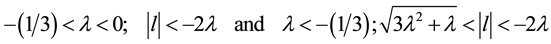
It should be mentioned that the modes 

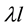
Remark (1): In the area VI in Figure 3: 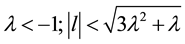
Three modes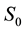
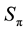
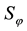


3. Modeling the Intermittent Turbulent Wake
3.1. Intermittent Wake of Weakly Coupled Streets
From the map in Figure 3 one can easily see that the alternating wake may be observed in wide triangle III:

Moreover, these are modes of in-phase 
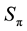
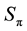
Figure 3. Map of regimes of two-cylinder wake: the mode AS exists in the domain I; S0 in II; S0 and Sπ in III; Sπ in IV; Sφ in V; VI is a nonphysical domain.
phase space. This task may be achieved by taking into consideration the following arguments. The boundary of these domains on 
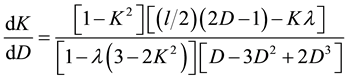
This special trajectory must joint unstable stationary points of set (12 - 14) with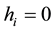

In real time the motion along the boundary is unstable. Accordingly, one has to distinguish between three possibilities when numerical calculating this boundary. In the first case, for the domain of the model parameters


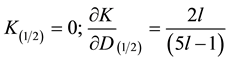

lutions merge at the point
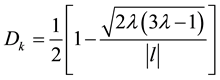
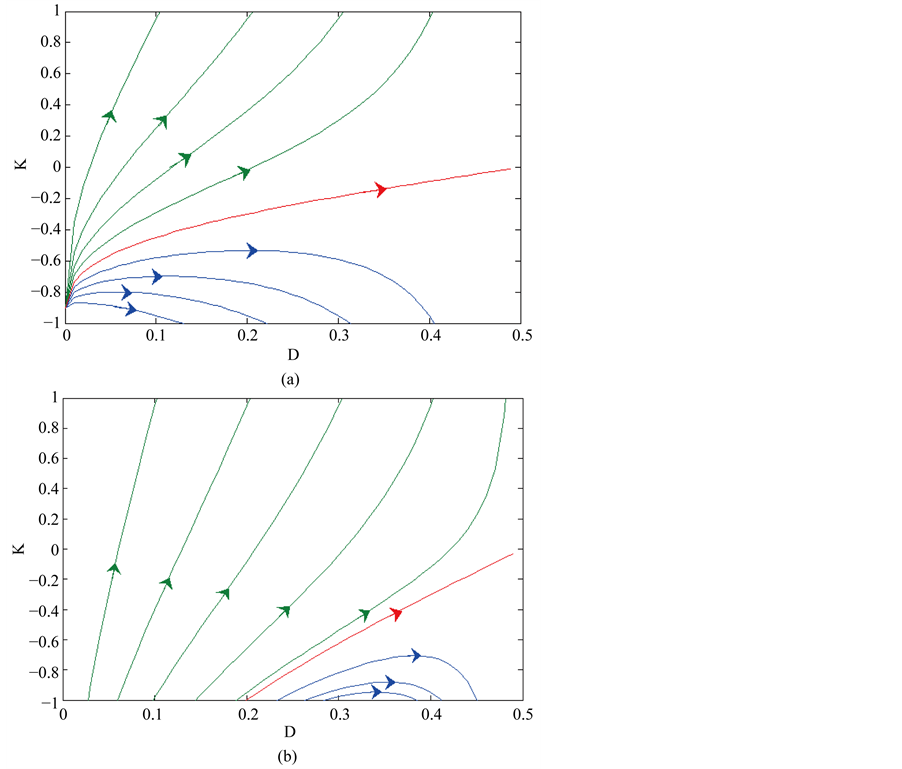
case. Some examples of numerical calculation of boundary curve are presented in Figure 4.
Here some comment may be done. The boundary curve 
tion of its variable D for positive values of its parameter 
tion of D for negative values of parameter 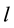
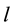


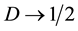
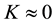


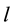
Now we are ready to evaluate the alternation coefficient of the wake within the framework of the model. Let the turbulence intensity of incoming flow be large. This factor is modeled by the right-hand sides of the Equations (1), (2), Equations (5)-(7) and Equations (12)-(14) according to the model developed. Then, for the case of strong interruptions regime, the mean residence time for each compete mode would be proportional to the area of the attraction domains for corresponding mode. Hence, for this case of strong incoming turbulence, the alternation coefficient of the wake may be defined as:

Here this alternation coefficient is defined by the emergence of the mode of anti-phase synchronized streets. (Somebody may prefer the coefficient 

Figure 4. Boundary of the attraction domains of modes in the phase space: (a) for case λ = 0.2; l = 0.2, (b) for case λ = 0.6; l = 0.2.
weakly coupled von Karman streets. In the case of first domain of parameters 

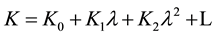
By this way one comes to relevant expansion of the alternation coefficient 


Here the new parameter 





Results of such numerical (dots) and analytical (solid curves) evaluation of the alternation coefficient 
Remark (1): Alternation coefficient is an odd function of parameter 


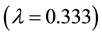
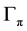
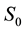

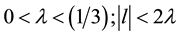
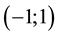


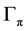


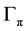


3.2. Intermittent Wake of Strongly Coupled Streets
When considering the case of strongly coupled von Karman streets

Fortunately, for this case, the general solution for the phase trajectory on 

Here C is an arbitrary constant. Figure 6 is the illustration of phase trajectories for the case. Here points 

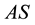
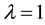

In the case 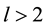

Figure 5. Intermittence coefficient Γπ as a function of the model parameters p = l/2λ and λ. The last parameter monotonically grows from low curve to top curve: λ = 0.01; 0.05; 0.1; 0.2; 0.333, respectively; whereas the first parameter p is positive for all curves.
Figure 6. Oscillators-streets dynamics for the case λ = 1; (a) for case l = 1.8, (b) for case l = 6.
For symmetric case 

These conclusions are easily seen from the form of general solution (34) of dynamic equations illustrated by Figure 6. Here upper line 


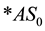
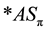






4. Approbation of the Model
The multiplicity of wake modes existing for two cylinders in side-by-side configuration is well known from the visualization experiments and as well as from simulations. The developed model managed to cover four global modes of the cylinders wake. There are modes of in-phase and anti-phase synchronized streets among four of them. It is known that these modes exist in the case of a relatively weak interaction of the von Karman streets formed by each cylinder when the cylinders are not so close to each other (see, for example [3] [29] ). And the intermittent wake regime of these two modes is known for some wake parameters, as well [29] . Our two-di- mensional wake model also brings to a restriction of existence domain of 



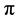


5. Model Application to Plasma Wake Studying
Formally, one has two possibilities when applying the model to cylinders intermittent wake. These are the cases of weekly (3.1) and strongly (3.2) coupled streets as it was discussed above. The variant of weekly interacting streets is not our case as the frequency splitting of the two observed modes was large enough ~30% (see Figure 2) for 




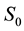

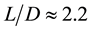
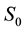
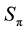



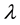

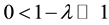


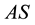
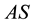




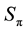
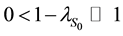
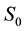

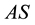



Realization ability of this scenario depends on amount of the plasma heating effect. The redistribution of power in the velocity spectra was observed at relatively low discharge power 
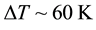




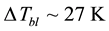





6. Results and Conclusions
At present the study of turbulent plasma wake behind a number of cylinders is in progress. Simple, easily treated, and physically justified model of two cylinders wake in the side-by-side arrangement has been proposed. Actual variant of this two-parametric model covers four global wake modes as well as the intermittent regime. This model works well for the case of weak coupling of the streets, and works worse at strong coupling. Nevertheless, within the framework of advanced model, the observed wake intermittent modes were identified for the pitch ratio value 
Main part of these results was briefly presented at the 26-th Symposium on Plasma Physics and Technology, Prague, June 2014.
Acknowledgements
Discussions with Prof. Eduard V. Teodorovich, numerical calculation by Kirill Yu. Osipenko and electronic circuitry work by Aleksandr A. Sirotin are gratefully acknowledged. This study was supported by The Russian Fund for the Basic Researches, grant 13-01-00742.
References
- Sumner, D. (2010) Journal of Fluids and Structures, 26, 849-899. http://dx.doi.org/10.1016/j.jfluidstructs.2010.07.001
- Alam, Md.M., Zhou, Y. and Wang, X.W. (2011) Journal of Fluid Mechanics, 669, 432-471. http://dx.doi.org/10.1017/S0022112010005288
- Peng, Y.F. (2013) Journal of Modern Physics, 4, 89-95. http://dx.doi.org/10.4236/jmp.2013.45B015
- Bao, Y., Zhou, D. and Tu, J. (2013) Computers & Fluids, 71, 124-145. http://dx.doi.org/10.1016/j.compfluid.2012.10.013
- Verma, A. and Mittal, S. (2011) Physics of Fluids, 23, Article ID: 121701. http://dx.doi.org/10.1063/1.3664869
- Zhao, M. and Cheng, L. (2014) Journal of Fluid Mechanics, 751, 1-37. http://dx.doi.org/10.1017/jfm.2014.268
- Assi, G.R.S., Bearman, P.W. and Meneghini, J.R. (2010) Journal of Fluid Mechanics, 66, 365-401. http://dx.doi.org/10.1017/S0022112010003095
- Song, L. and Wu, S. (2013) Applied Mechanics and Materials, 275-277, 482-485. http://dx.doi.org/10.4028/www.scientificnet/AMM.275-277.482
- Luzzatto-Fegiz, P. and Williamson, C.H.K. (2012) Physics of Fluids, 24, Article ID: 066602. http://dx.doi.org/10.1063/1.4724307
- Choi, H., Jeon, W-P. and Kim, J. (2008) Annual Review of Fluid Mechanics, 40, 113-139. http://dx.doi.org/10.1146/annurev.fluid.39.050905.110149
- Corke, T.C., Enloe, C.L. and Wilkinson, S.P. (2010) Annual Review of Fluid Mechanics, 42, 505-529. http://dx.doi.org/10.1146/annurev-fluid-121108-145550
- Moreau, E. (2007) Journal of Physics D: Applied Physics, 40, 605-636. http://dx.doi.org/10.1088/0022-3727/40/3/S01
- Jukes, T.N. and Choi, K.S. (2009) Physics of Fluids, 21, Article ID: 084103. http://dx.doi.org/10.1063/1.3194307
- Sosa, R., Artana, G., Benard, N. and Moreau, E. (2011) Experiments in Fluids, 51, 853-860. http://dx.doi.org/10.1007/s00348-011-1108-0
- Sidorenko, A.A., Budovskii, A.D., Postnikov, B.V., Zverkov, I.D., Zanin, B.Yu., Kozlov, V.V. and Maslov, A.A. (2010) Technical Physics Letters, 36, 304-307. http://dx.doi.org/10.1134/S106378501004005X
- Raizer, Yu.P. (1991) Gas Discharge Physics. Springer-Verlag, Berlin.
- Panchenko, V.Ya., Zavalov, Yu.N., Galushkin, M.G., Grishaev, R.V., Golubev, V.S. and Dubrov, V.D. (2006) Laser Physics, 16, 40-51. http://dx.doi.org/10.1134/S1054660X0601004X
- Huang, H. and Wang, Y. (2010) Optical Engineering, 49, Article ID: 114201. http://dx.doi.org/10.1117/1.3509163
- Osipov, A.I., Uvarov, A.V. and Vinnichenko, N.A. (2006) Physics of Fluids, 18, Article ID: 105106. http://dx.doi.org/10.1063/1.2364261
- Gembarzhevskii, G.V. (2009) Technical Physics Letters, 35, 241-244. http://dx.doi.org/10.1134/S1063785009030146
- Siddon, T.E. and Ribner, H.S. (1965) AIAA Journal, 3, 747-749. http://dx.doi.org/10.2514/3.2963
- Peschard, I. and Le Gal, P. (1996) Physical Review Letters, 77, 3122-3125. http://dx.doi.org/10.1103/PhysRevLett.77.3122
- Landa, P.S. (1996) Nonlinear Oscillations and Waves in Dynamical Systems. Kluwer Academic Publishers, Dordrecht.
- Albarede, P. and Provansal, M. (1995) Journal of Fluid Mechanics, 291, 191-222. http://dx.doi.org/10.1017/S0022112095002679
- Gembarzhevskii, G.V. (2009) The Effect of Flow Structure Transformation Induced by Electric Discharge and Its Simple Model. Contributed Papers, VI International Conference on Plasma Physics and Plasma Technology, Vol. 1, Minsk, 28 September-2 October 2009, 27-30.
- Nayfeh, A.H. (1981) Introduction to Perturbation Techniques. John Wiley & Sons, Hoboken.
- Gembarzhevskii, G.V. and Lednev, A.K. (2013) Reduced Order Model for Effect of Pulsation Energy Redistribution in Cylinders Wake Induced by Glow Discharge. Proceedings of the 12th Workshop on Magneto-Plasma Aerodynamics, Moscow, 26-28 March 2013, 41-44.
- Pikovsky, A., Rosenblum, M. and Kurths, J. (2002) Synchronization: A Universal Concept in Nonlinear Science. Cambridge University Press, Cambridge.
- Williamson, C.H.K. (1985) Journal of Fluid Mechanics, 159, 1-18. http://dx.doi.org/10.1017/S002211208500307X
- Gembarzhevskii, G.V. (2011) Technical Physics Letters, 37, 19-22. http://dx.doi.org/10.1134/S1063785011010020
- Kim, H.J. and Durbin, P.A. (1988) Journal of Fluid Mechanics, 196, 431-448. http://dx.doi.org/10.1017/S0022112088002769
- Le Gal, P., Chauve, M.P., Lima, R. and Rezende, J. (1990) Physical Review A, 41, 4566-4569.
- Provansal, M., Mathis, C. and Boyer, L. (1987) Journal of Fluid Mechanics, 182, 1-22. http://dx.doi.org/10.1017/S0022112087002222
- Schlichting, H. (1955) Boundary Layer Theory. Pergamon Press Ltd., London.
- Budaev, V.P., Savin, S.P. and Zelenyi, L.M. (2011) Physics-Uspekhi, 54, 875-918. http://dx.doi.org/10.3367/UFNe.0181.201109a.0905