Journal of Modern Physics Vol.06 No.03(2015), Article ID:54203,7
pages
10.4236/jmp.2015.63030
How to Demonstrate the Lorentz Factor: Variable Time v.s. Variable Inertial Mass
Olivier Serret
ESIM Engineer, Cugnaux, France
Email: o.serret@free.fr
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 1 February 2015; accepted 16 February 2015; published 25 February 2015
ABSTRACT
For a century, hypothesis of a variable time is laid down by the Relativity Theory. This hypothesis can explain many Nature observations, experiments and formulas, for example the Lorentz factor demonstration. Because of such good explanations, the hypothesis of a variable time has been validated. Nevertheless, it remains some paradoxes and some predictions which are difficult to measure, as a reversible time or the time variation itself. The purpose of this article is to study another hypothesis. If it gives interesting results, it would mean that this alternative hypothesis can also be validated. The idea in this paper is to replace the variable time by a variable inertial mass. To the difference with the Theory of Relativity (where the inertial mass and the gravitational mass are equal and variable), the gravitational mass is here supposed to be constant. So, starting from the definition of the kinetic energy, it is introduced the Lorentz factor. And then it is demonstrated the value of the Lorentz factor thanks to a variable inertial mass. This variable inertial mass can also explain experiments, like Bertozzi experiment. If this alternative demonstration was validated, it could help to open doors, other physical effects could be explained like the addition of velocities.
Keywords:
Lorentz Factor, Variable Time, Relativity, Light Celerity, Inertial Mass, Mass of Inertia, Gravitational Mass, Bertozzi, Michelson and Morley

1. Introduction
“They’re cheering us both, you because nobody understands you, and me because everybody understands me” would have told Chaplin to Einstein.
To try after all to understand some bases of the Relativity Theory, we can read Einstein’s book: “La relativité” [1] . An important step is the demonstration of the Lorentz factor:
 (1)
(1)
where this Lorentz factor come from, and why is it so important?
Let us have a short historic.
In 1851, trying to prove the existence of aether, Fizeau found a rule to add the
velocity, and gave an important place of the ratio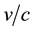 , with
, with
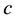 the light celerity in vacuum and
the light celerity in vacuum and
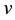 the light velocity in the medium.
the light velocity in the medium.
In 1862, Maxwell introduced the constant
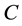 in his equations.
in his equations.
In 1881, Michelson tried to prove the existence of aether, without success.
In 1892, to explain this failure, Lorentz introduce the contraction of the length
from a factor
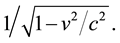
In 1902, Poincaré wrote there was no absolute space and no absolute time.
In 1902, Abraham and Kaufmann announced the apparent mass of electron increase with motion.
In 1904, Lorentz did calculations with a dilatation of time and an increase of mass in motion.
In 1905, Einstein published the first part of the Theory of the Relativity, demonstrating the Lorentz factor, the rule of addition of velocities, and many other physical points.
In 1915, Einstein published in a memory the second part of the Theory of Relativity where the inertial mass was equal to the gravitational mass.
It is because the use of the Lorentz factor can help to explain many experiments and Nature observations that it is so important. And this demonstration of Lorentz factor is based on a variable time.
We will try here to demonstrate the Lorentz factor without using a variable time.
In the historical account of Lorentz factor here before, scientists of the previous century did three kinds of hypotheses:
・ a variation of length with motion;
・ a variation of time with motion;
・ a variation of mass with motion.
In the Theory of Relativity, demonstration of Lorentz factor is based on the first two hypotheses (the variation of mass was an indirect consequence). In present work, we take the hypothesis of a variation of the inertial mass with motion, but with a constant gravitational mass. The originality of this work is we will not use any variation of time or of length, (in the Newtonian mechanics, there is not either variation of time and of length). If this demonstration is acceptable, then it will be shown how to explain some experiments: Bertozzi, Michelson and Morley, Fizeau.
2. Context and Definitions
2.1. The Time
According to the Theory of Relativity, time is variable from one inertial reference frame to another. However, there is no “direct” measure of any such phenomenon. And a reversal of time, an “imaginary” time, a dilatation or a contraction of time―all of them are only explanations of experiments, and not direct measures of these phenomena. And they create a serious difficulty: Relativity Theory has variable time, while Quantum Mechanics has an invariable time; but there is only a single physical world. Two opposite theories on one topic, i.e. time, make an incoherent situation in Physics.
In Newtonian theory, and in modern Quantum Mechanics, time is “universal”, meaning that it is the same in all frames of reference. That hypothesis of a universal time is taken in the present article too.
2.2. The Length
In Newtonian theory, space has three dimensions and these dimensions are constant whatever the reference frame can be. In Relativity theory, the space (called space-time) has four dimensions including time, and these dimensions are variable according to the reference frame. In particular, the length of the space is decreasing with the velocity, i.e. with the kinetic energy. It is always a bit surprising because when calorific energy is added to a body, its length is increasing.
Anyway, in present article, the space is constant as it can be in Newtonian mechanics.
2.3. The Masses
a) The word “mass” is used to describe two different physical effects [2] :
・ One mass measures the ability to generate gravitational attraction; it is a static
mass, called “gravitational mass”, ;
;
・ Another mass measures the resistance to the modification of movement; it is a
dynamic mass, called “inertial mass”,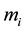 .
.
b) In Newtonian Mechanics,
 (2)
(2)
c) In Relativity Theory [3] ,
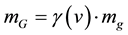 (3)
(3)
with
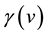 being the Lorentz factor [5] of Equation (1).
being the Lorentz factor [5] of Equation (1).
And
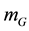 the mass in motion,
the mass in motion,
And
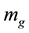 the motionless mass.
the motionless mass.
And it is postulated in Relativity Theory [1] that inertial mass and gravitational mass are equal.
d) The mass hypothesis of this article is:
・ Gravitational mass is the same in all reference frames, as it is in Newton’s mechanics.
・ Inertial mass is variable, growing with the kinetic energy, or the velocity, of
the object. So inertial mass is really different from gravitational mass: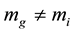 .
.
Let
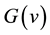 be a function such that
be a function such that
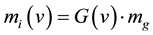 (4)
(4)
with

which means that when the body is motionless,

2.4. The Celerity of Light
In the Theory of Relativity, there are two meanings for the symbol c:
・

・

In this present essay, c is the speed of light, but c is not the constant asymptotic value of the speed v of any massive body. So another variable s is defined here as the asymptotic value of speed v. To further distinguish the two concepts, c is called “celerity” (of light), and s is called (asymptotic) “speed” [4] .
In the Earth frame, the light celerity in vacuum is measured as


2.5. Comparison of Hypotheses
Let us sum up the different hypotheses of the three theories in Chart 1.
Present hypothesis will be called “VIM” for Variable Inertial Mass.
3. Demonstration of the Lorentz Factor
3.1. Definitions and Usual Properties
Some definitions or properties are usual:
Chart 1. Comparison of hypotheses.
The velocity, or speed, is

The impulse, or linear momentum, is

The force, or strength, is

The work done over a length


The kinetic energy is the energy of the body less the energy of the body motionless
(with


3.2. Additional Hypotheses
A so famous equation links the Energy of a body to its Mass:

It is not specified if it is the gravitational mass or the inertial mass because in Relativity Theory, the two masses are equal.
We can note that this equation does not request a variable time or a variable length; it could also be written, using the fact light is an electromagnetic phenomenon:

with

And

In this paper, we have distinguished the values of the inertial mass from the gravitational mass, and the light celerity from the asymptotic speed. So we will do the hypothesis that the Energy of the body is linked to the inertial mass by:

3.3. Demonstration
Let us start with Equation (4):
By definition [cf Equation (12)] the kinetic energy is the energy of a body without its energy motionless:

Due to the equivalence of different forms of energy, some work can be transformed into a variation of kinetic energy:






By definition of the velocity [cf Equation (8)]:




The inertial factor


3.4. Reciprocal Demonstration
Still without using a variable time, let us calculate Lorentz factor and then the Total Energy:
Let us start by an obvious equality:

Introducing






This equation is well-known in Relativity Theory to be the norm of the quadri-vector
(of course with


So, using the symbol of Lorentz factor, previous Equation (30) can be written:

or

with



All these expressions have been demonstrated without using a variable time, only considering a variable inertial mass.
3.5. Application
Then we can calculate the increase of inertial mass in function of speed, as shown in Figure 1.
For example, the fastest man-made object ever built, the spacecraft Helios 2, reached 250,000 km/h [5] , or 70 km/s, or 0.00023 c. At this velocity, its inertial mass increased of 0.01 g out of 270 kg, or 0.000006%, which is still very difficult to detect.
4. Some Experiments Explained without Using a Variable Time
4.1. Experiments v.s. Nature Observations
Figure 1. Inertial mass as a function of speed.
4.2. Bertozzi’s Experiment
The Lorentz factor


we can correlate [see Figure 2] experimental results with the function:

Function which is equivalent to

or

The difference between Bertozzi’s experiment results and the hereafter curve of

4.3. Michelson and Morley’s Experiment
The Michelson and Morley experiment [8] [9] is also given as a proof of the Theory of Relativity. This experiment was done to prove the existence (or not) of aether. If aether exists, the velocity of light along one path should be different than that along a perpendicular path. No evidence of such difference emerged, so, this experiment served to prove that aether did not exist.
Figure 2. Bertozzi’s experiment: velocity increases asymptotically to a limit.
Since the duality wave-particle theory (this theory did not exist in Michelson’s era), it is accepted than the light can spread in vacuum (i.e. without aether). So photons running the same distance with the same velocity can be explained simply within Newton’s mechanics; Michelson and Morley experiment can be explained without a variable time.
4.4. Fizeau’s Experiment
Trying also to prove the existence of aether, Fizeau did the first experiment with light and water in motion [10] . He found a rule to add the velocities which clearly invalid the Newtonian law of velocity addition. If the expression of Fizeau rule is different, the results will be extremely closed to the predictions of the Relativity Theory; so Fizeau experiment has been given by Einstein as a proof of the Theory of Relativity.
Next step in this essay would be to try to demonstrate or to find a law of addition of velocities without using a variable time…
5. Conclusions
The purpose of this article was to demonstrate the Lorentz factor without using a variable time. Whereas Newtonian mechanics and Relativity Theory agree on the equality of the inertial mass with the gravitational mass, it is here taken the hypothesis of their difference. Abraham and Kaufmann, and then Bertozzi, have already in their experiment established the increase of inertial mass with the velocity. The originality of this article is to suppose a constant gravitational mass when inertial mass increases.
The Lorentz factor is introduced with the link between the kinetic energy and the inertial mass. Then some definition and properties of the velocity, the impulse, the strength, the work and the kinetic energy are applied to very small variations by calculus. By this way, Lorentz factor can be demonstrated.
If there is no error in the equations, this would give coherence between the time of the traditional mechanics and the time of the Quantum Mechanics.
Mainly, it would open alternative explanations to experiments and Nature observations. Next step will be to demonstrate the addition of velocities without using a variable time.
References
- Einstein, A. (1979) La Relativité. Édition Payot.
- Serres, M. and Farouki, N. (1997) Le Trésor―Dictionnaire des Sciences. Ed. Flammarion, 554.
- (2014) Laboratoire d’Astrophysique de Marseille, Relativité Restreinte. http://astronomia.fr/6eme_partie/RelativiteRestreinte.php#masse
- Serret, O. (2012) Mass of Inertia and Kinetic Energy. http://gsjournal.net/Science-Journals/Research%20Papers-Relativity%20Theory/Download/4113
- Helios Spacecraft. http://en.wikipedia.org/wiki/Helios_(spacecraft)
- Bertozzi, W. Speed and Kinetic Energy of Relativistic Electrons. http://muj.optol.cz/richterek/data/media/ref_str/bertozzi1964.pdf
- Bertozzi Experiment. http://en.wikipedia.org/wiki/Tests_of_relativistic_energy_and_momentum
- Michelson-Morley Experiment. http://scienceworld.wolfram.com/physics/Michelson-MorleyExperiment.html
- Michelson and Morley. Influence of Motion of the Medium on the Velocity of Light. http://en.wikisource.org/wiki/Influence_of_Motion_of_the_Medium_on_the_Velocity_of_Light
- Fizeau, H. Hypothèses relatives à l’éther lumineux. http://www.orgonelab.org/EtherDrift/Fizeau1851.pdf






