Journal of Modern Physics
Vol.5 No.14(2014), Article
ID:49020,16
pages
DOI:10.4236/jmp.2014.514128
Variational Principle in the Quantum Statistical Theory
Eduard A. Arinshteyn
Tyumen State University, Tyumen, Russia
Email: earin@inbox.ru
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 4 June 2014; revised 2 July 2014; accepted 19 July 2014
ABSTRACT
In the present paper, a generalization of the method of partial summation of the expansion of the thermodynamical potential is proposed. This generalization allows one to obtain the corresponding equations for higher-order correlation matrices, as well as to formulate the variational method for their solution. We show that correlation matrices of equilibrium quantum system satisfy a variational principle for thermodynamic potential which is functional of these matrices that provides a thermodynamic consistency of the theory. This result is similar to a variational principle for correlation functions of classical systems.
Keywords:Generating Functional, Density Matrices, Correlations, Irreducible Part, Variational Method

1. Introduction
A progress of the classical statistical theory of the condensed systems is obliged to use the method of partial density and correlations.
A few papers were devoted to the quantum generalization of this theory. For example F. Bloch and C. De Dominicis have proposed a method of the quantum group expansion, similar and practically identical to the method of the group expansion in the classical statistical physics [1] -[3] . C. D. Lee and C. N. Yang have carried out the partial summation of this expansion [4] that allowed one to analyze the system of particles with short range strong repulsion (gas of hard spheres) taking into account the terms up to second order. A. Isichara has calculated also the first terms in the expansion of partial density matrices by using this method [5] .
But now these works have only historical, but not practical interest. The majority of the papers in the field of modern quantum statistical theory are utilizing the Green function method differing from the above basic method of the classical theory. L. Kadanoff proposed to describe the quantum system properties in a vicinity of a critical point with the help of the Green function method [6] [7] . K. Wilson used a renormalization group method [8] [9] . This method allows also constructing the 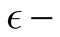 and 1/n-expansions for critical parameter calculations.
and 1/n-expansions for critical parameter calculations.
Two-points (one-particle) Green functions contain essential information regarding the elementary excitation dynamics. However, determining of these functions allowing one to obtain the full information regarding the system properties, requires to determine the higher-order Green functions, in particular, the four-point (binary) ones. Besides, determining of the elementary excitations can be inaccurate in the case of their large density and intensive interaction. The problem of determining of binary correlation remains actual also for the method of density function when analyzing the multi-electron systems [10] .
Technical problems related to the Green function method, are forcing to look for alternative approaches to describe complex quantum systems. One of such approaches in the theory of equilibrium quantum systems is the partial density matrix method being the quantum analogue of the method of partial density functions in classical systems.
This method gives the full information regarding thermodynamic properties of a system, omitting detailed information (compared to the method of Green functions) regarding the elementary excitation dynamics. At the same time, the above loss of the dynamic information allows one to reach the sufficient progress in calculations of system statistical properties in the broad region of parameters and conditions.
The regular method allowing to calculate the expansion of arbitrary accuracy degree, and to produce the equations for partial density matrix which are similar to the integral equations for classical partial distribution functions, is proposed. This method is based on the generating functional method for partial density matrix.
Properties of unary density matrix of an equilibrium quantum system are considered in the paper [11] . In this paper the expansion for generating functional of density matrix is obtained; the partial summation of the complete unary matrix expansion is fulfilled; the variational principle for thermodynamic potential, equivalent to the equation to which this matrix satisfies, is formulated. On the base of the equation for complete unary matrix, the partial summation of the internal lines in the equation for thermodynamic potential and generating function of all density matrices is obtained. The higher-order correlation matrices are presented in this paper only in the view of expansion over unary density.
The development of a method consists of research of all partial density matrices. This generalization allows one to obtain the corresponding equations for higher-order correlation matrices, as well as to formulate the variational method for their solution.
This method is a generalization of a variational principle of the classical theory [12] for the case of quantum systems.
2. The Generating Functional Method
To describe the operators and the matrices determining a many particle system, the method of generating functional is utilized. This method is considered in details in the paper [11] . Let’s list the results and notations of this paper, used below.
The particle creation and annihilation operators in the case of one-particle state, characterized by a set of discrete or continuous quantum numbers , are denoted as
, are denoted as  and
and , as usually. These operators satisfy the standard permutation conditions: the commutative for Bozeand anti-commutative ones for Fermiparticles, respectively.
, as usually. These operators satisfy the standard permutation conditions: the commutative for Bozeand anti-commutative ones for Fermiparticles, respectively.
The generating functional for the matrix elements of any operator
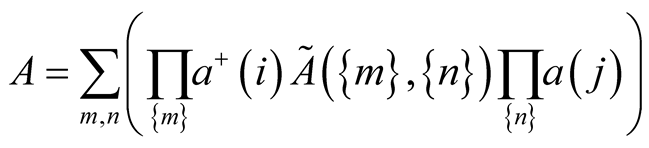 (1)
(1)
in the representation of secondary quantization takes the form
 (2)
(2)
where 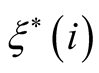 and
and 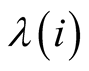 are basic functions depending on the same set of quantum numbers as the operators of creation and annihilation,
are basic functions depending on the same set of quantum numbers as the operators of creation and annihilation, 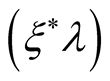 is a scalar product in the Hilbert space of an one-particle state. In the case of Fermi-statistics these functions are the generatrices of the Grassmann-algebra, anti-commutative with each other and with the operators of creation and annihilation of Fermi-particles. The values
is a scalar product in the Hilbert space of an one-particle state. In the case of Fermi-statistics these functions are the generatrices of the Grassmann-algebra, anti-commutative with each other and with the operators of creation and annihilation of Fermi-particles. The values  (a function of a set of quantum numbers) are the factors of the normal expansion. A multiplier
(a function of a set of quantum numbers) are the factors of the normal expansion. A multiplier 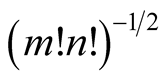 or
or 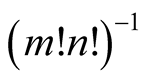 can be extracted sometimes from these factors.
can be extracted sometimes from these factors.
The relations
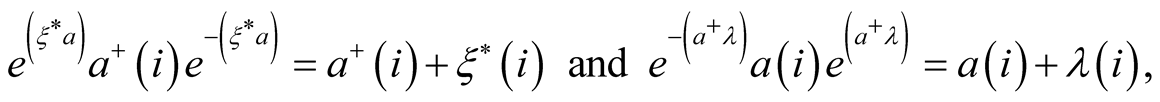
which can be established by the expansion on the functions  and
and , result in
, result in
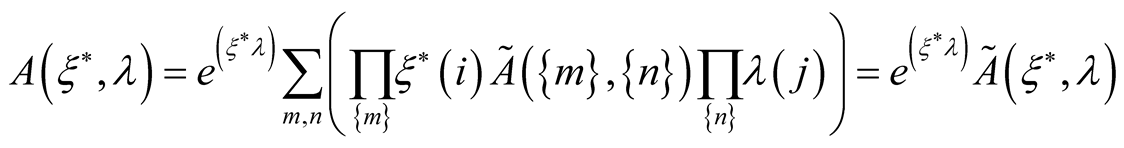 (3)
(3)
so 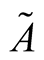 is generating functional of the normal expansion factors.
is generating functional of the normal expansion factors.
By introducing a functional convolution
 (4)
(4)
we present the operator 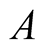 as:
as:
 (5)
(5)
and the spur of the operator as:
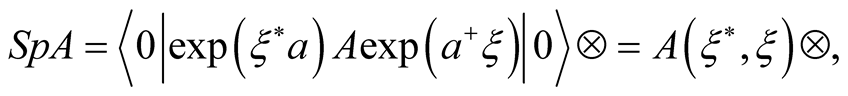 (6)
(6)
the hidden function  in the convolution being transferred cyclically to the right or the function
in the convolution being transferred cyclically to the right or the function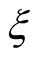 —to the left in the case of Fermi-statistics. Notice that a hidden function is always convoluted with its conjugate.
—to the left in the case of Fermi-statistics. Notice that a hidden function is always convoluted with its conjugate.
The conformity
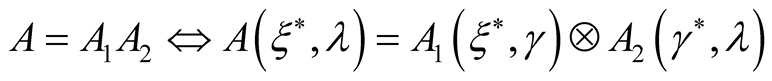 (7)
(7)
follows from the Representation (5).
The generating functional for the irreducible parts of the matrix elements of an operator 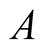 is defined by the relation:
is defined by the relation:
 (8)
(8)
If the functionals in the Expressions (6) and (7) are presented using their irreducible parts, the convolution will be factorized into a product of unconnected parts. The usual calculation of the factors of each type [11] results in the theorem on connected parts for the spur of an operator:
 (9)
(9)
and for a convolution of two functionals
 (10)
(10)
In case of the mixed state what characterized by a statistical operator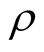 , the average of physical value is equal to
, the average of physical value is equal to
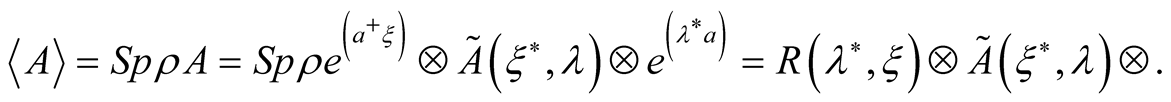 (11)
(11)
The functional
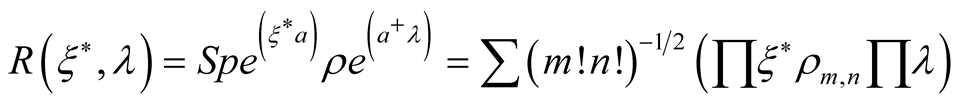 (12)
(12)
is the generating functional for partial density matrices.
Introducing a representation
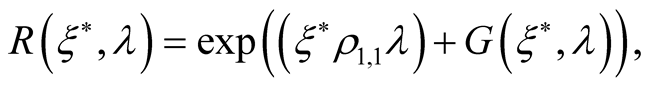 (13)
(13)
where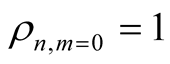 ;
; 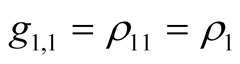 is an unary density matrix, one can define a generating functional
is an unary density matrix, one can define a generating functional  for correlation matrices which are irreducible parts of multiparticle density matrices.
for correlation matrices which are irreducible parts of multiparticle density matrices.
Equilibrium Systems
The density matrix  of system in a statistical equilibrium is diagonal one. In the case of system of the particles with zero spin, all partial densities, and the correlations are the functions. In the case of system of particles with non-zero spin, the component number of the partial density matrices and the correlations equals to total spin. For example, in the case of an electron system, the binary matrix has two components corresponding to the singlet and triplet states. In doing so, a spin density matrix of the total spin
of system in a statistical equilibrium is diagonal one. In the case of system of the particles with zero spin, all partial densities, and the correlations are the functions. In the case of system of particles with non-zero spin, the component number of the partial density matrices and the correlations equals to total spin. For example, in the case of an electron system, the binary matrix has two components corresponding to the singlet and triplet states. In doing so, a spin density matrix of the total spin  has the view
has the view 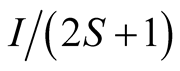 [13] (it is proportional to the unit matrix and has the unit spur
[13] (it is proportional to the unit matrix and has the unit spur ). The physical meaning in this case is the following: the electron pair system contains two subsystems. The spin of the electron pair with opposite-oriented spins is equal to zero, the spin state is anti-symmetric one, and, therefore, the relative orbital state consists of the even spherical harmonics. The spin of electron pair with identical spins is equal to unit, the spin state is symmetric one, and, therefore, relative orbital state consists of the odd spherical harmonics. The electron correlation functions and electron interactions inside of one subsystem and the ones between distinct subsystems are different. Thus, this property of binary correlation function takes into account exchange effects.
). The physical meaning in this case is the following: the electron pair system contains two subsystems. The spin of the electron pair with opposite-oriented spins is equal to zero, the spin state is anti-symmetric one, and, therefore, the relative orbital state consists of the even spherical harmonics. The spin of electron pair with identical spins is equal to unit, the spin state is symmetric one, and, therefore, relative orbital state consists of the odd spherical harmonics. The electron correlation functions and electron interactions inside of one subsystem and the ones between distinct subsystems are different. Thus, this property of binary correlation function takes into account exchange effects.
The statistical operator of equilibrium ideal gas looks like
 (14)
(14)
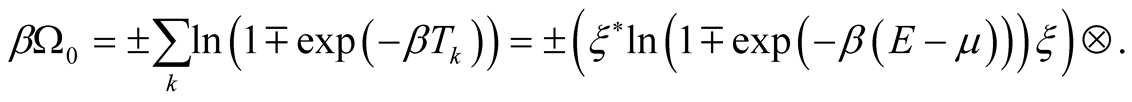
This expression is the decision of a variational task for the functional

at the performance of a condition , where
, where  is an inverse temperature and the upper sign is used in case Bose systems, lower--in case Fermi ones. Thus
is an inverse temperature and the upper sign is used in case Bose systems, lower--in case Fermi ones. Thus
 (15)
(15)
The Gibss distribution is defined by the statistical operator

were 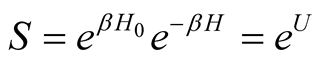 is a Mathubara temperature dispersion operator and operator
is a Mathubara temperature dispersion operator and operator 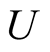 allows to find a classical potential energy analogue.
allows to find a classical potential energy analogue.
Partial density matrices are diagonal:

where  is partial density function,
is partial density function,  or
or .
.
From Bloch equation 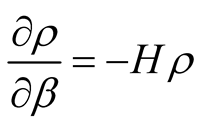 where
where 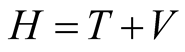 and
and 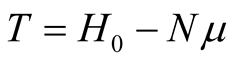 follows
follows

The Mathubara operator is determined for Hamiltonian spectrum limited from below including ones having interactions with strong pushing away on small distances (hard core).
Let’s introduce irreducible parts of the functional :
:
 (16)
(16)
Then
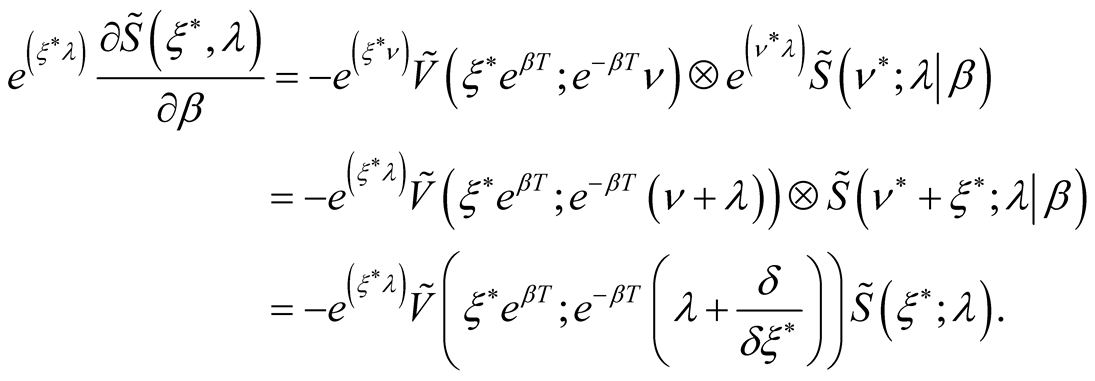 (17)
(17)
As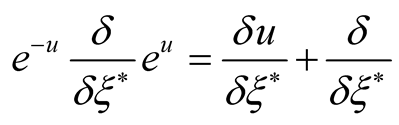 , so
, so
 (18)
(18)
and as  from this follows
from this follows
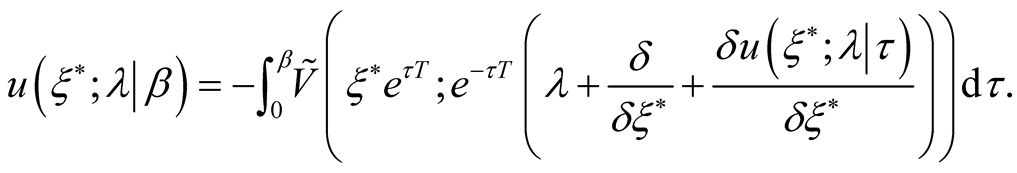 (19)
(19)
If Hamiltonian save particle numbers then

that is that  breaks up into one, two, three, ... -partial diagonal on number of particles irreducible parts having the appropriate identical order on functions
breaks up into one, two, three, ... -partial diagonal on number of particles irreducible parts having the appropriate identical order on functions  and
and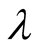 . The two-partial irreducible part coincides with binary nucleus obtained by Jang and Lee by summation of infinite subsequence members of a series of the perturbation theory [4] and also is the decision of a two bodies task
. The two-partial irreducible part coincides with binary nucleus obtained by Jang and Lee by summation of infinite subsequence members of a series of the perturbation theory [4] and also is the decision of a two bodies task
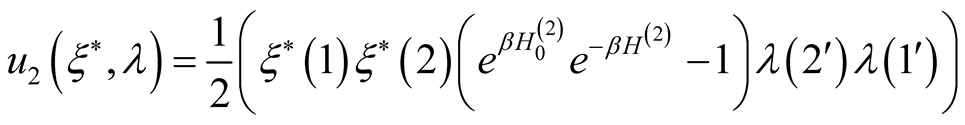 (20)
(20)
Senior irreducible parts require the decision of appropriate  -partial tasks for the determination or can be found by expansion on binary nucleuses consecutively for
-partial tasks for the determination or can be found by expansion on binary nucleuses consecutively for .
.
Generally if Hamiltonian does not save particles numbers for example in photon or phonon cases then functional  contain members of a kind
contain members of a kind  off-diagonal on particles numbers. Let’s notice, that these matrices are some analogue of classical effective potentials but not Mayer functions ones.
off-diagonal on particles numbers. Let’s notice, that these matrices are some analogue of classical effective potentials but not Mayer functions ones.
The statistical sum of interacting particles system looks like:
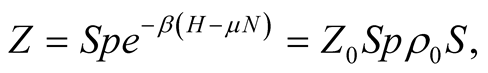 (21)
(21)
From Representation (16) and ratio  we got:
we got:
 (22)
(22)
From this follows
 (23)
(23)
where 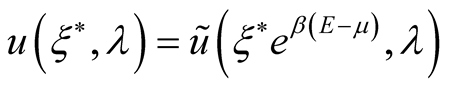 and
and 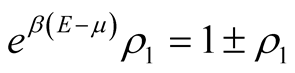 The functional
The functional 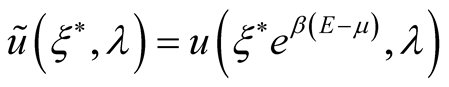 defines irreducible parts of hermitian operator
defines irreducible parts of hermitian operator  as an opposite to the functional
as an opposite to the functional 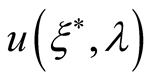 which defined nonhermitian Mathubara one. For example
which defined nonhermitian Mathubara one. For example
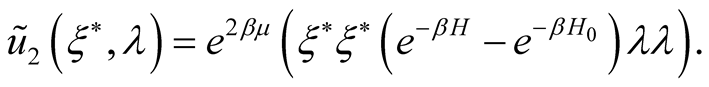
Expansion (23) is quantum generalization of classical one on density degrees. C. D. Lee and C. N. Yang have got two first members by summation of infinite subsequence of a expansion on binary nucleuses [4] .
Similarly we obtain the expansion of partial density matrices, more precisely—generating functional of these matrices:
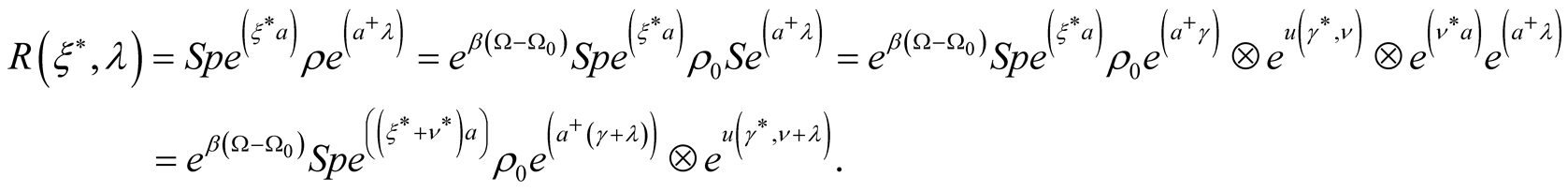 (24)
(24)
This give the expansion:
 (25)
(25)
It is necessary to take into account, that in the scalar product 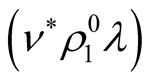 the function
the function  is cyclically transferred to the right at convolution whereas the function
is cyclically transferred to the right at convolution whereas the function 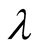 remains at the left. Hence, at obvious performance of cyclic transition on the right there is a multiplier
remains at the left. Hence, at obvious performance of cyclic transition on the right there is a multiplier . In a result we have got
. In a result we have got
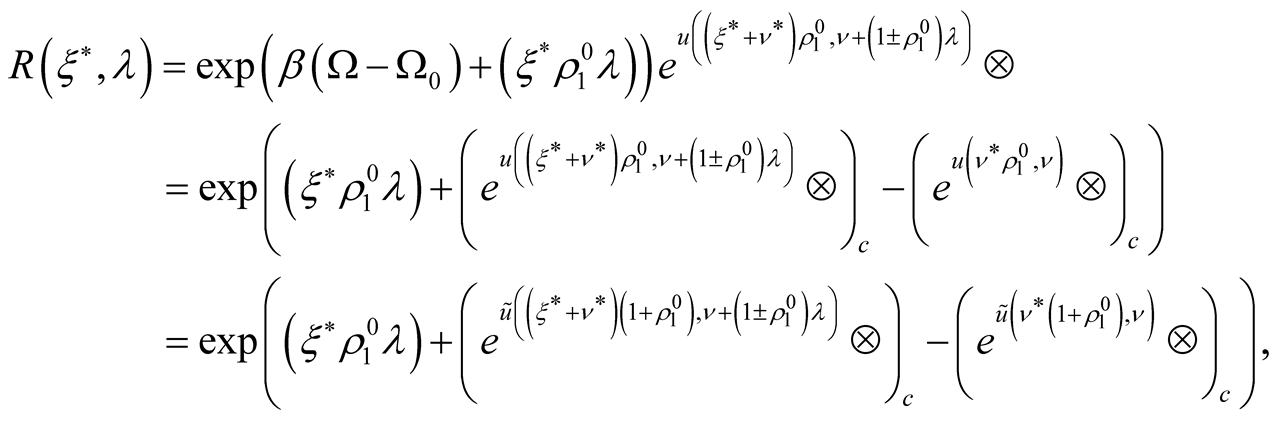 (26)
(26)
where the signs are determined by statistics as usual.
As matrices  are diagonal so correlation matrices
are diagonal so correlation matrices  and irreducible parts
and irreducible parts 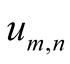 are diagonal too. The off-diagonal matrix elements of the irreducible parts are excluded at averaging.
are diagonal too. The off-diagonal matrix elements of the irreducible parts are excluded at averaging.
The above expansion of all density matrices is a quantum generalization of the expansion of partial distribution functions, and transforms into the last one in the case of the classical limit. A. Isihara has obtained the first terms of the expansion for unary, binary and three-particle density matrices by summation of quantum group expansion [5] .
The method of partial summation in the expansion of the unary density matrix is considered in the paper [11] . The expansion of the thermodynamic potential and of the partial density matrix over the 1-irreducible diagrams is obtained; and determining of the thermodynamic potential and of full unary density matrix or effective single-particle energy is reduced to the unified variational problem. This expansion is a quantum analogue of the virial Mayer expansion over irreducible integrals.
3. Variational Principle
The obtained quantum virial expansion has the finite convergence radius like in the classical case. An enlargement of the region of the applicability of this expansion, and of its partial summation is possible when applying the expansion over correlation matrices in place of virial expansion, as each such a matrix is the sum of infinite number of the terms in the virial expansion. Such a transition appears possible thanks to validity of a variational principle for the thermodynamic potential being a functional of the correlation matrices.
The problem of determining of correlation matrices can be reduced to a variational problem due to the relationship between the statistical sum (thermodynamic potential) 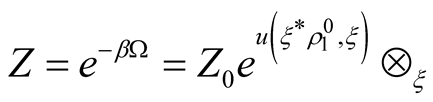 and the generating functional of the partial density matrices.
and the generating functional of the partial density matrices.
The expression for a complete variation of the statistical sum in the dependence from a variation of potentials (including the members of all orders) looks like
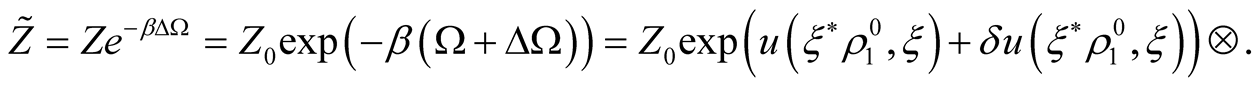
The identity  is valid. Let’s designate on this basis an “internal” convolutions for functionals
is valid. Let’s designate on this basis an “internal” convolutions for functionals  and
and 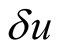 and the convolution between these functionals by different variable. As a result we obtain
and the convolution between these functionals by different variable. As a result we obtain

where


Whence follows
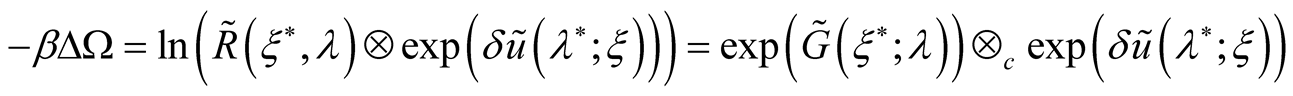 (27)
(27)
Thus we obtain an expansion of a thermodynamic potential complete variation on degrees of potentials variations:

Whence follows
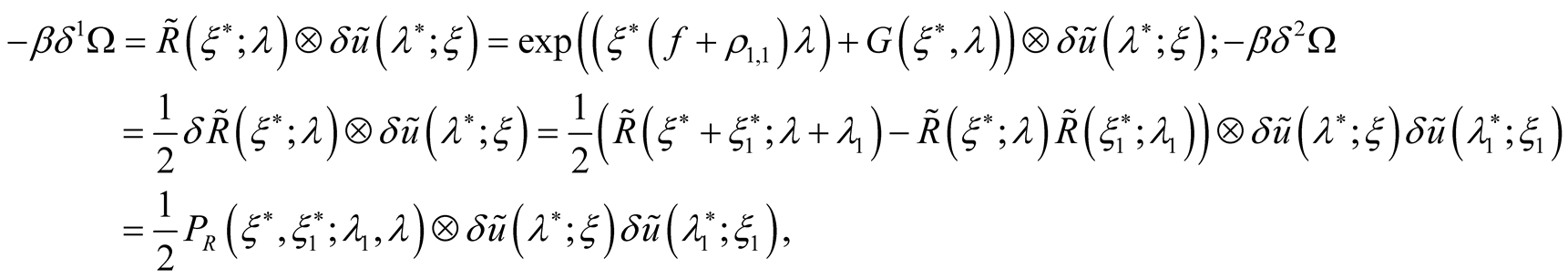 (28)
(28)
which determine a variation  of the functional
of the functional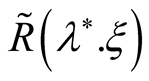 :
:
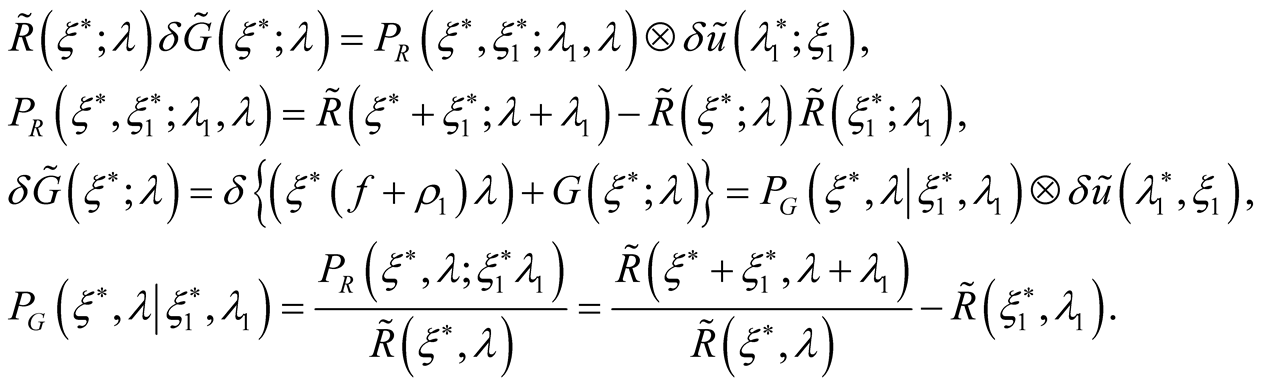 (29)
(29)
The first variation 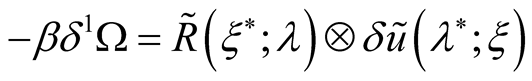 determines all partial density matrices similarly to an appropriate expression of the classical theory depending on effective potentials:
determines all partial density matrices similarly to an appropriate expression of the classical theory depending on effective potentials:  The second variation determine functional derivations of partial density matrices with the respect on effective potentials
The second variation determine functional derivations of partial density matrices with the respect on effective potentials .
.
The further transformations are similar to classical case [12] . The partial summation of virial expansion is carried out by transition to expansion on correlation matrices. The transition to the correlation matrices as independent variables is carried out by Legendre transformation
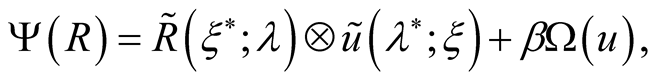
as a result of this the functional 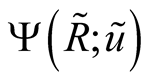 dependents from density matrices (it means
dependents from density matrices (it means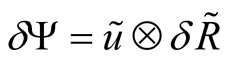 ) under the condition of extremeness
) under the condition of extremeness , determining functionals
, determining functionals 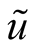 and
and 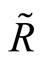 connection. The inverse transformation
connection. The inverse transformation

also looks like a variational task , resulting in the same ratio between functionals
, resulting in the same ratio between functionals  and
and 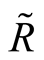 presented in other (inverse) form. It means that the equations, determining partial density matrices depending on interactions, basically are reduced to a variational task for a thermodynamic potential as a functional from these matrices. However such transition requires determination of an obvious kind of dependence
presented in other (inverse) form. It means that the equations, determining partial density matrices depending on interactions, basically are reduced to a variational task for a thermodynamic potential as a functional from these matrices. However such transition requires determination of an obvious kind of dependence 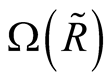 and
and .
.
For the decision of this task it is necessary to invert the linear system (29) and thus to find derivatives of old independent variables 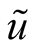 with respect to new ones
with respect to new ones . For this purpose it is required to find functionals (matrices)
. For this purpose it is required to find functionals (matrices)  and
and  inverse to ones (the matrices)
inverse to ones (the matrices)  and
and  from the equations
from the equations
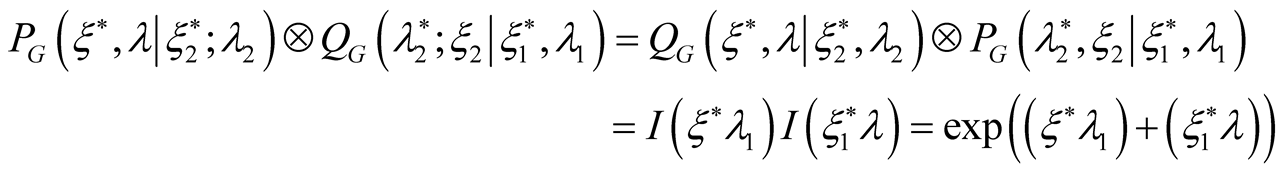 (30)
(30)
This gives a relation

which determines the derivatives of old variables  with respect to new ones.
with respect to new ones.
One can extract a unite functional from the functional :
:

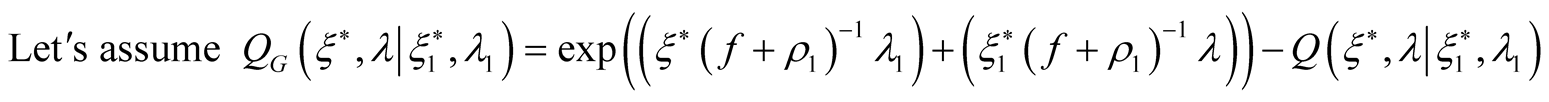
and we have a generalized quantum O-Z ratio

An obvious kind of expression for thermodynamic potential in dependencies on partial density or correlation matrices (and on functional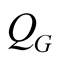 ) we obtain entering in expression for density matrices auxiliary parameter
) we obtain entering in expression for density matrices auxiliary parameter , thus
, thus 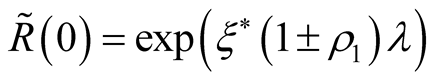 and
and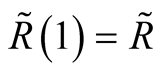 . The simplest way is a replacement
. The simplest way is a replacement
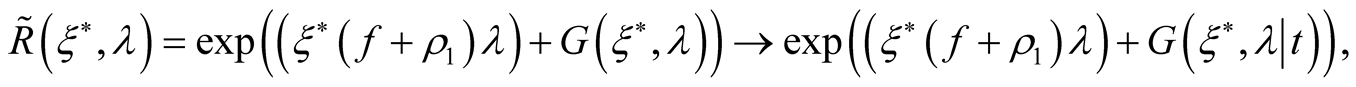
for example 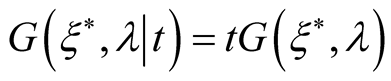 or
or 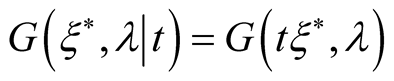
Then we obtain the system of the integral equations for density matrices
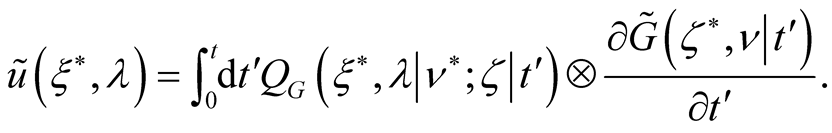 (31)
(31)
This implies to
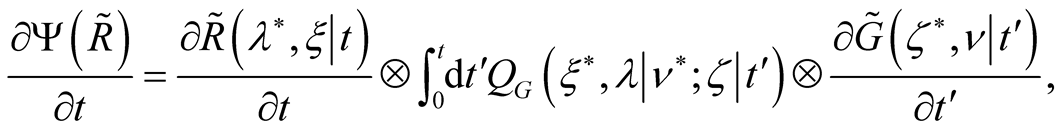

and the functional of the variational task is
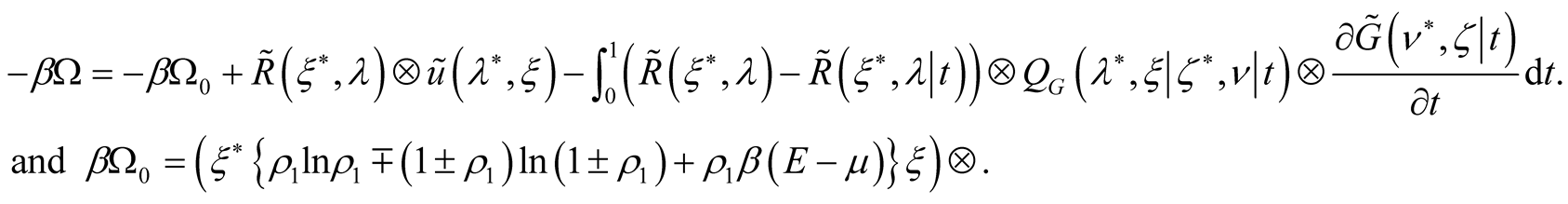 (32)
(32)
Thus, the task of definition of density and correlation matrices is reduced to the variational task for the thermodynamic potential—Function (32) at additional condition (30).
From this task we can pass to an unconditional variational task. At any meaning of an auxiliary parameter we transfer the right side of the Equation (30) to the left, convolute obtained expression with the functional  (uncertain multiplier), integrate on the auxiliary parameter and combine with the Equation (30). So we obtain
(uncertain multiplier), integrate on the auxiliary parameter and combine with the Equation (30). So we obtain
 (33)
(33)
In this expression the three functionals ,
, 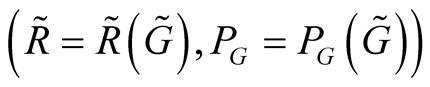 ,
, 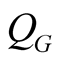 and
and 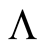 vary independently. Variation on
vary independently. Variation on 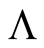 gives the Equation (30), variation on
gives the Equation (30), variation on 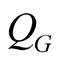 results in the equation
results in the equation

That gives
by convolution with functional 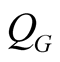 on the basis of the Equation (30).
on the basis of the Equation (30).
This expression substitution in the Expression (32) results in the functional of unconditional variational task for the thermodynamic potential.
 (34)
(34)
Thus, the problem of determining of the thermodynamic functions, and correlation matrices in the quantum system is reduced to an unified variational problem: either conditional or unconditional ones. In the second case, an additional condition determining relationship between functionals 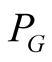 and
and , is a result of the variational principle: the variation of the functional
, is a result of the variational principle: the variation of the functional 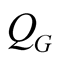 should be equal to zero.
should be equal to zero.
The structure of the obtained functional of the variational problem (more exactly, of the thermodynamic potential of a quantum system) is similar to the one in the case of a classical system. The transition to the new functional variables (such as, the correlation matrices), and determining of equation system of successive approximations do not practically differ from the corresponding procedure in the case of a classical systems [12] .
Like to the classical case, the method of the successive diagonalization for the matrices  and
and , results in equation system of successive approximations for variational functional.
, results in equation system of successive approximations for variational functional.
 (35)
(35)
where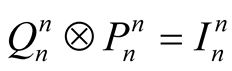 ; and
; and
 (36)
(36)
The matrices orders designations coincide with functions orders ones in the article [7] . It is obvious that 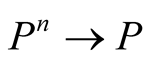 and
and  if
if .
.
4. Potential of Effective Interaction in the Frohlich Model
We shall consider the method of the effective potential calculation on the example of the well known Frohlich model of the two-component electrons and phonons system.
The unperturbed Hamiltonian of the system is

 and
and  are electron creation and annihilation operators,
are electron creation and annihilation operators, 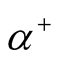 and
and  are longitudinal phonons ones,
are longitudinal phonons ones,  ,
,  an one-electron energy
an one-electron energy  includes an interaction with a field of a lattice, but does not take into account an electron-phonon interaction. The electron-phonon interaction of this model is determined by two vertexes:
includes an interaction with a field of a lattice, but does not take into account an electron-phonon interaction. The electron-phonon interaction of this model is determined by two vertexes:
 (37)
(37)
where 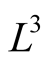 is a volume of the system, an electron spin at dispersion from a state
is a volume of the system, an electron spin at dispersion from a state  in a
in a  one does not change,
one does not change, . In each vertexes the electron quantity and momentum are kept but numbers of phonons changes. The electron momentum and the phonon wave vector are determined is the first Brillouin zone.
. In each vertexes the electron quantity and momentum are kept but numbers of phonons changes. The electron momentum and the phonon wave vector are determined is the first Brillouin zone.
Consequently the functional  is
is
 (38)
(38)
where an  index correlates to electronic (grassman) and
index correlates to electronic (grassman) and 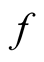 one—to phonon variables. If a spin preserves so
one—to phonon variables. If a spin preserves so
 (39)
(39)
 is a same momentum function.
is a same momentum function.
The Equations (18) and (19) for the irreducible parts  of the functional
of the functional  are nonlinear. Separate out the right part of the Equation (18) the member that doesn’t contain functional
are nonlinear. Separate out the right part of the Equation (18) the member that doesn’t contain functional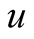 , and linear on
, and linear on  one we receive the equation
one we receive the equation
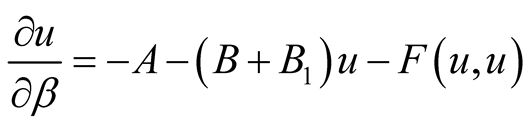 (40)
(40)
where
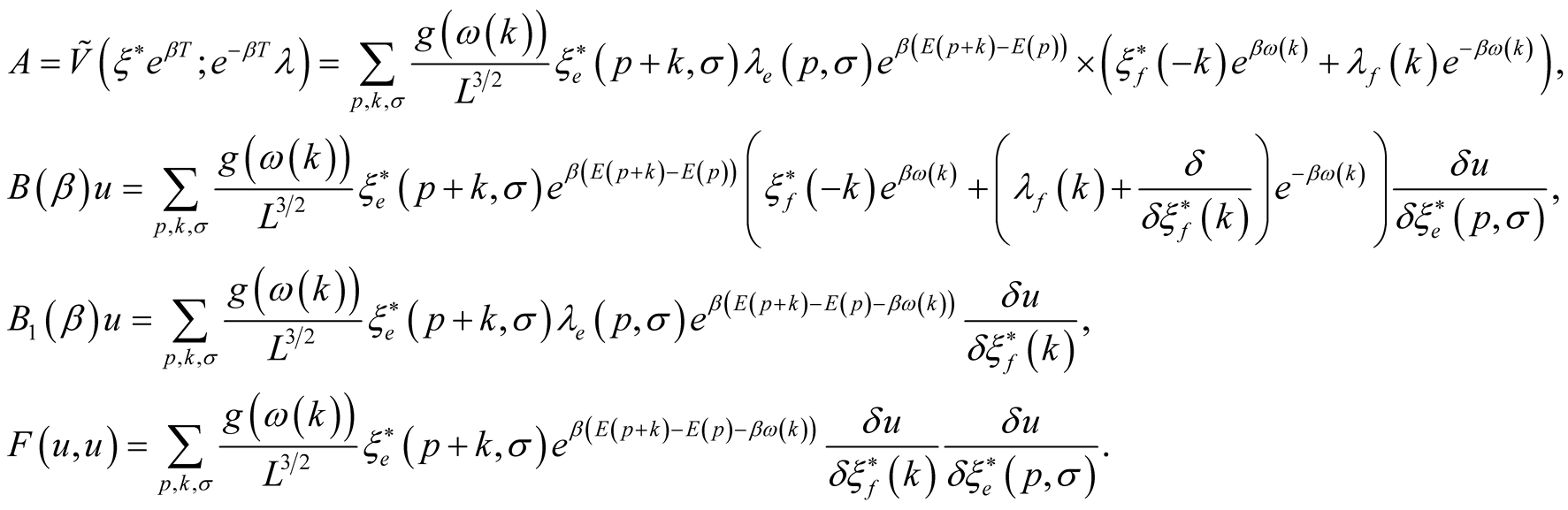
As the interaction doesn’t change the electron number so , where
, where 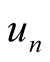 has an identical order
has an identical order  on the functions
on the functions 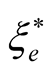 and
and , determining the final and initial electron states, and the Equation (40) determines consistently all
, determining the final and initial electron states, and the Equation (40) determines consistently all . Every
. Every  are qualities of phonon functions
are qualities of phonon functions ,
,  in the final and initial states. The operator
in the final and initial states. The operator 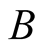 does not change a number of the electronic functions pairs
does not change a number of the electronic functions pairs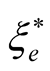 ,
,  (electronic lines), the operator
(electronic lines), the operator 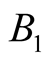 increases the number of such pairs by one. As a result we can find the functionals
increases the number of such pairs by one. As a result we can find the functionals  from a sequence of the equations:
from a sequence of the equations:
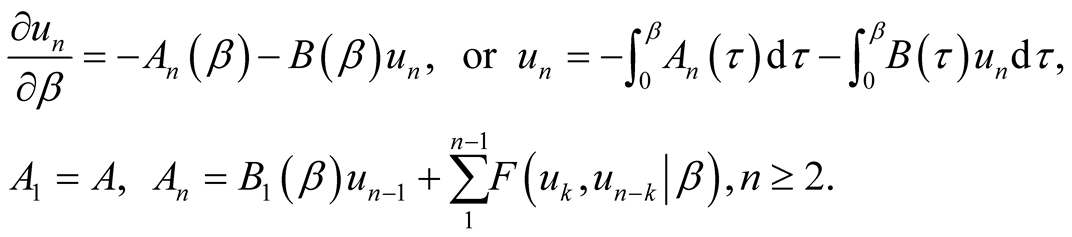
It is possible to present the decision of these equations in the form
 (41)
(41)
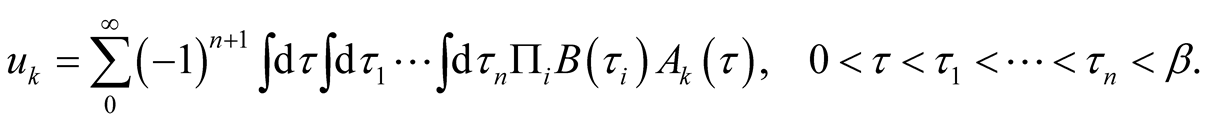 (42)
(42)
The integrals of these expressions are rather cumbersome though are calculated elementary. The general method of these integrals calculation is given in the appendix.
The members  determine an effective electrons interaction,
determine an effective electrons interaction,  ones if
ones if  determine processes of creation, absorption and dispersion of phonons by single electrons and by electron groups, that can represent an interest at the description of any kinetics processes.
determine processes of creation, absorption and dispersion of phonons by single electrons and by electron groups, that can represent an interest at the description of any kinetics processes.
Thus we shall receive the first order members
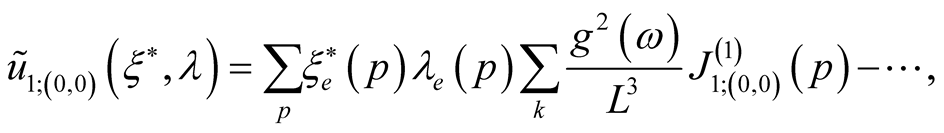

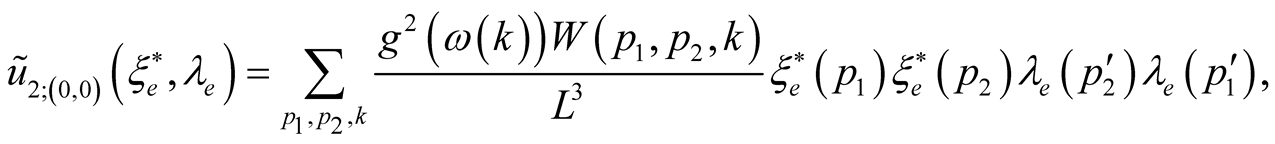

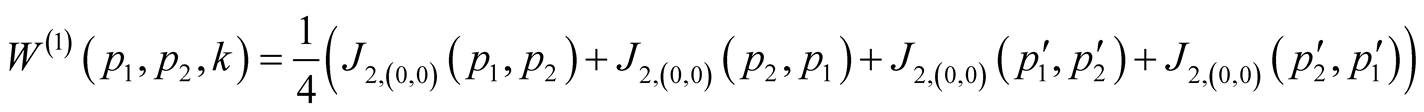


Thus it appears, that

as
 (43)
(43)
so

It means that the effective pair electron interaction is an attraction.
In view of the symmetry of a matrix element 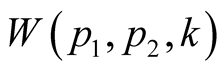 we shall receive
we shall receive
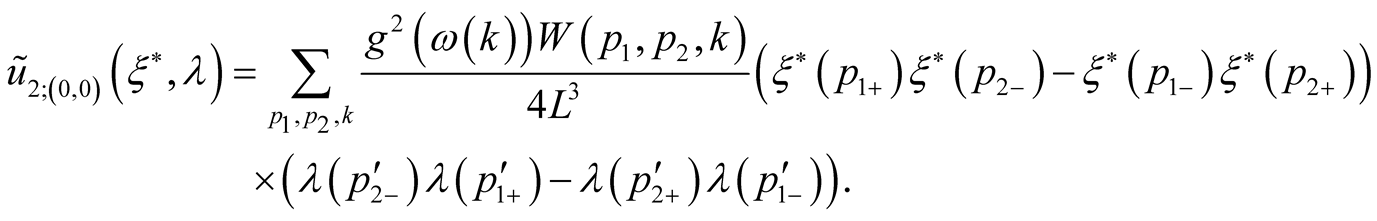 (44)
(44)
From this expression it is visible, that the Frohlich model describes the electron attraction in singlet state with zero spin.
Thus, we have received the effective potential energy of electron interaction by the phonon exchange.

The sum  determines the contribution of this interaction in the thermodynamic potential of system.
determines the contribution of this interaction in the thermodynamic potential of system.
The members 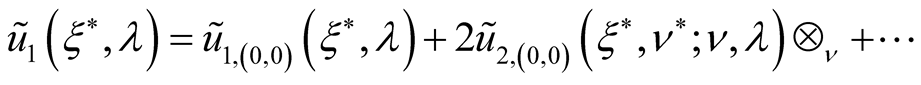 determine an additional one-electron effective energy.
determine an additional one-electron effective energy.
The members  determines the effective interaction of electron pairs with opposite spins.
determines the effective interaction of electron pairs with opposite spins.
The functions 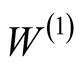 and
and  aren’t small, when
aren’t small, when . In this case, the accounting only of the first terms in the expansion is insufficient. The representation (48) (see Appendix) allows one to fulfill a partial summation of the obtained expansions, but this problem lies out of the framework of present paper. It is obvious, that summation of the expansion of the operator
. In this case, the accounting only of the first terms in the expansion is insufficient. The representation (48) (see Appendix) allows one to fulfill a partial summation of the obtained expansions, but this problem lies out of the framework of present paper. It is obvious, that summation of the expansion of the operator 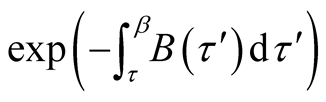 (41) allows one to determine all high-order terms in the expansion of the functional
(41) allows one to determine all high-order terms in the expansion of the functional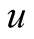 . This summation renormalizes the one-electron energy
. This summation renormalizes the one-electron energy , as well as the vertex
, as well as the vertex , but doesn’t modify the basic properties of the effective electron interaction.
, but doesn’t modify the basic properties of the effective electron interaction.
Thus, the electron-phonon interaction results in the effective electron attraction which acts in a thin energy layer near to the Fermi-surface: 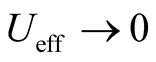 if
if , and effective (active) electron density
, and effective (active) electron density

so the modification of the electron state is impossible because of the Pauli principle.
5. Superconductive Electron Pairs Formation.
Let’s consider application of the offered variational approach on a known not trivial case: superconductive electron pairs formation. This effect can be the result of the attraction of electrons with opposite spins [14] [15] . These pairs are created by electrons of a thin energy layer adjacent to a Fermi-level (Cooper). We shall consider conditions of formation of such pairs.
Some symmetry exists between electron states with opposite momentums and spins: the operators  and
and 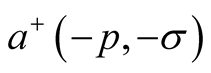 change a charge, momentum and spin of systems equally. The linear combination of these operators works in the same way. This combination is determined by the Bogoljubov transformation [16]
change a charge, momentum and spin of systems equally. The linear combination of these operators works in the same way. This combination is determined by the Bogoljubov transformation [16]
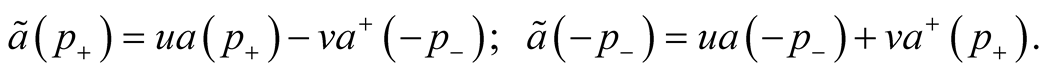
These new operators submit correct anticommutative relations if the conditions  are executed. In particular, it is possible to put
are executed. In particular, it is possible to put
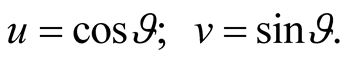
It is evident that ;
; . The inverse transformation has the same form with change of a sign of an angle
. The inverse transformation has the same form with change of a sign of an angle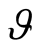 .
.
If 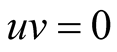 (
(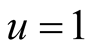 ,
,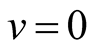 outside of a Fermi-surface and
outside of a Fermi-surface and ,
, 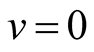 inside this surface) this is the electron distribution on energy in normal conductors. It doesn’t depend on a spin. The electronic system is considered as the electrons and holes system and the symmetry isn’t shown.
inside this surface) this is the electron distribution on energy in normal conductors. It doesn’t depend on a spin. The electronic system is considered as the electrons and holes system and the symmetry isn’t shown.
If the electron interaction depends on a spin it is possible symmetry violation and the stable state will appear at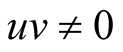 . It is conditions of superconductivity pairs formation. The Frolich model describe such interaction.
. It is conditions of superconductivity pairs formation. The Frolich model describe such interaction.
One can consider the Bogoljubov transformation as a turning of a two-dimensional vector 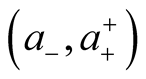 on an angle
on an angle 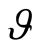 and vector
and vector —on a
—on a 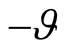 one. Two-dimensional scalar products
one. Two-dimensional scalar products
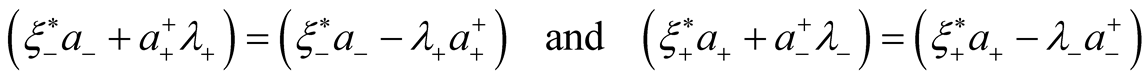
are invariants that determines the turning of the vector  on an angle
on an angle 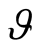 and the vector
and the vector —on a
—on a 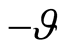 one. Hence
one. Hence
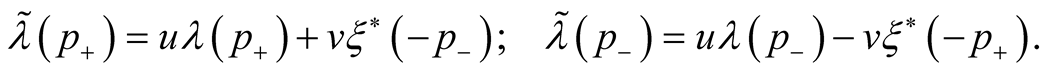

Parameters 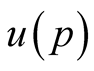 and
and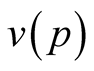 , (or meanings of the angles
, (or meanings of the angles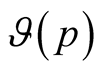 ) follow from the variational principle for the part of the thermodynamic potential which does not contain correlations as the correlations vary independently:
) follow from the variational principle for the part of the thermodynamic potential which does not contain correlations as the correlations vary independently:
 (45)
(45)
Here 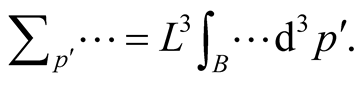 Rather bulky expressions for the certain members of this equation are given in the Appendix.
Rather bulky expressions for the certain members of this equation are given in the Appendix.
Replacement ,
,  reduces this task to well known nonlinear integral equation for energy gap
reduces this task to well known nonlinear integral equation for energy gap 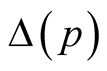
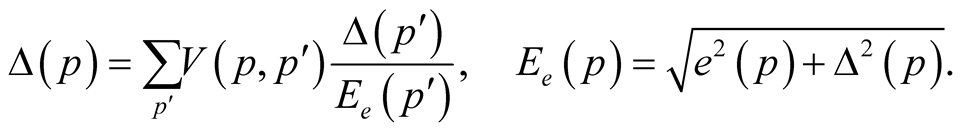 (46)
(46)
The decision  determines appearance of superconductivity. Detailed analysis of this equation is given in the extensive literature on the superconductivity theory [16] .
determines appearance of superconductivity. Detailed analysis of this equation is given in the extensive literature on the superconductivity theory [16] .
6. Conclusions
The difference in the analysis methods in the cases of the classical and quantum systems is caused by two reasons. The first one is related to the quantum concepts of the permutation symmetry and quasi-particles, absent in the case of classical systems. More critical dissimilarity between these cases is the difference in the interactions between classical particles and quantum quasi-particles that is reflected in the Hamiltonian functions. As a result, many problems for the systems of one class are of no importance for the ones of the other class, and opposite ones. Nevertheless, the analogy between the methods, utilized for the classical and quantum theory, is kept. This analogy reflects also the situation where the Gibbs distribution is true in the both cases (classical and quantum ones), and this fact can be of high importance.
The important common property of classical and quantum systems is the applicability of the variational principle. This principle establishes that all essential parameters of both classical, and quantum systems (such as correlations, and order parameters) are being determined by the requirement of the minimum of the thermodynamic potential. The transition method from the description of a system state by utilizing of the dynamic variables (coordinates, and momentums) to the description by utilizing of new ones (correlation functions) is the same one, namely, Legendre transformation.
One of the advantages of the variational method is the opportunity to utilize the models based on the some or other physical reasons, and determining of model parameters by direct methods. Such an approach in the statistical physics isn’t a new one. It is enough to refer the Landau theory for the second order phase transitions. At the same time, it is a hard problem to demonstrate all possibilities of the variational principle within the framework of a sole paper, and this task requires the further work.
The doubtless advantage of a method consists of an opportunity of more correct determination of the correlations and research of the effects, connected to them.
References
- Bloch, F. and De Dominicis, C. (1958) Nuclear Physics, 7, 495; (1952), 10, 509.
- Balian, C., Bloch, F. and De Dominicis, C. (1963) Nuclear Physics, 25, 529; (1961), 27, 294.
- Bloch, F. (1965) Studys in Statistical Physics, III, 3-21.
- Lee, C.D. and Yang, C.N. (1959) Physical Review, 113, 1165; (1959), 116, 25.
- Isichara, A. (1968) Progress of Theoretical and Experimental Physics, 44, 1; (1969), Physical Review, 172, 166.
- Kadanoff, L.P. and Baym, G. (1962) Quantum Statistical Mechanics. New York.
- Kadanoff, L.P. (1975) Physical Review Letters, 34, 1005-1021. http://dx.doi.org/10.1103/PhysRevLett.34.1005
- Wilson, K.G. (1971) Physical Review D, 3, 1818. http://dx.doi.org/10.1103/PhysRevD.3.1818
- Wilson, K.G. (1973) Physical Review D, 7, 2911. http://dx.doi.org/10.1103/PhysRevD.7.2911
- Kohn, W. (1999) Reviews of Modern Physics, 71, 59-77. http://dx.doi.org/10.1103/RevModPhys.71.S59
- Arinshtein, E.A. (2002) Theoretical and Mathematical Physics, 130, 45-53. http://dx.doi.org/10.1023/A:1013876314504
- Arinshteyn, E.A. (2011) Journal of Statistical Physics, 144, 831-845. http://dx.doi.org/10.1007/s10955-011-0275-y
- Blum, K. (2010) Density Matrix Theory and Applications. Springer, Berlin.
- Ziman, J.M. (1972) Principles of the Theory of Solids. Cambridge University Press, Cambridge. http://dx.doi.org/10.1017/CBO9781139644075
- Schrifer, J.R. (1964) Theory of Superconductiviry. Benjamin, New York.
- Bogoljubov, N.N. (1958) Il Nuovo Cimento, 7, 794-805. http://dx.doi.org/10.1007/BF02745585
Appendix
A1. Integrals
It is possible to interpret all members of the functional 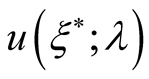 expansion in the terms of the diagram techniques. All diagrams contain continuous electronic lines directed on the imaginary time axis from
expansion in the terms of the diagram techniques. All diagrams contain continuous electronic lines directed on the imaginary time axis from 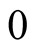 (function
(function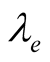 ) up to
) up to 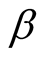 (function
(function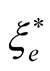 ), changing a momentum in each vertex. There aren’t any electronic lines having a return direction and internal ones. Phonon line has opening and end at
), changing a momentum in each vertex. There aren’t any electronic lines having a return direction and internal ones. Phonon line has opening and end at  (function
(function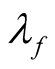 ) and
) and  (function
(function ), or in vertexes of the diagram at imaginary times
), or in vertexes of the diagram at imaginary times ;
;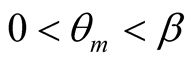 . Each of
. Each of  vertexes of the diagram include a multiplier
vertexes of the diagram include a multiplier

where ,
,  are energies determined by all entering and all leaving lines,
are energies determined by all entering and all leaving lines,  is performed and momentum keeps in vertex. The integration made on imaginary time meanings of all vertexes.
is performed and momentum keeps in vertex. The integration made on imaginary time meanings of all vertexes.
It is more convenient to calculate functional  and pass to integration on lengths of segments of imaginary axis connecting vertexes:
and pass to integration on lengths of segments of imaginary axis connecting vertexes:

Each segment 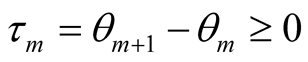 of the imaginary time axis brings in a multiplier
of the imaginary time axis brings in a multiplier  where
where  is the sum of energies of all lines located on this segment, thus
is the sum of energies of all lines located on this segment, thus . Integration on all
. Integration on all  variable
variable 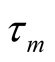 will be carried out under an additional condition
will be carried out under an additional condition .
.
Integrals of a kind  under condition
under condition 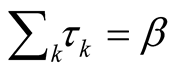 at all
at all  will be transformed generally as follows:
will be transformed generally as follows:
 (47)
(47)
(The integration contour on 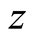 is closed in the upper half-plain.)
is closed in the upper half-plain.)
So
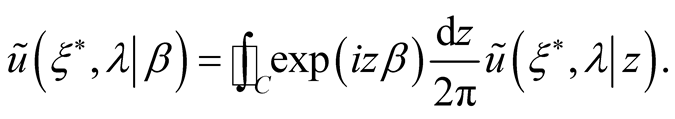 (48)
(48)
Functional  contains products of fractions of the form
contains products of fractions of the form .
.
If some 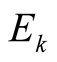 coincide for example
coincide for example 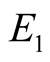 and
and 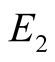 are we shall receive
are we shall receive
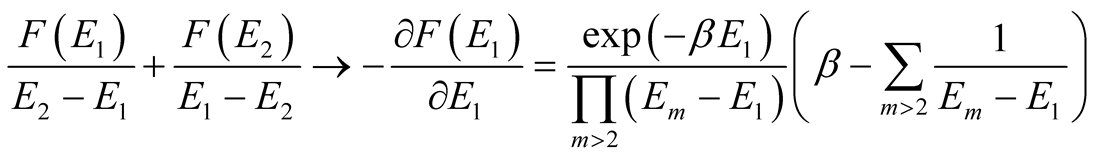
directly or calculating a residue of the second order pole. Calculation are similar if more poles coincide.
A2. Equation Members
For brevity we shall enter the designations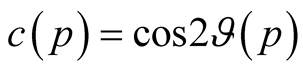 ,
, 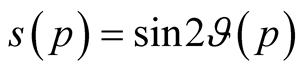

We shall present two first members of the functional 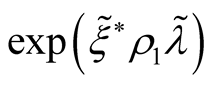 dispersion:
dispersion:


Then

Let as open expression for convolutions in last member:

A variational task functional contains also the member
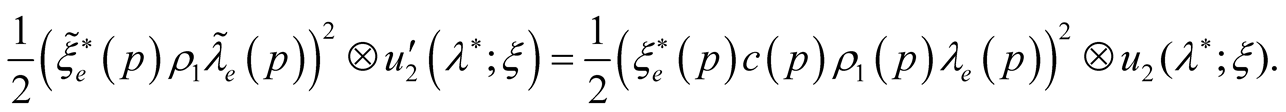
We shall show that it can be neglected. We have

and

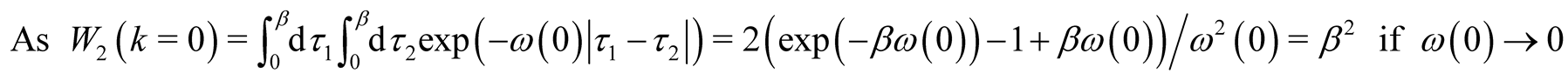
hence this member describes additional thermodynamic potential change (at fluctuations of zero frequency) and it can be neglected believing that .
.

