ABSTRACT

When a theory, as the general relativity, linked to special relativity, is foundation of a scientific paradigm, through normal science and academy, scientifics, professionals, professors, students and journals of that scientific community, the paradigm, it self-sustains and reproduces. Thus, the research is obligated and limited to apply the model existent of the paradigm to formulate problems and solve them, without searching new discoveries. This self-protection of the paradigm causes it to end its cycle of life, only after a long time, until that arise unresolved anomalies, some presents since origin, that they finally cause its change by other new paradigm. In this work, we study the most important anomalies that are part of the foundations of general relativity with the goal of promoting the call period of transition that is previous to scientific revolution. We use critical analysis method for rereading the general relativity, from the perspective of the history of science and philosophy of science. We find, the structural and complex anomaly of general relativity based on metaphysical spacetime that produces the metaphysics replaces physics. Also, two internal anomalies their direct consequences. These are: matter curves metaphysical spacetime, and metaphysical spacetime determines the geodesic motion of physical matter. We conclude that general relativity has no valid physical concept of spacetime, therefore of gravity. For these reasons, a new paradigm is needed.

Keywords:Relativity, Spacetime, Gravity, Physics, Metaphysics, Paradigm, Scientific Revolution

1. Introduction

Science is divided into factual and formal science. The first seeks the objective knowledge, i.e. knowledge of reality. The last studies the ideal entities that are created by thought.

The scientists of a particular factual science only can do its scientific practice through a set of recognized theories. These theories form its basis that must be conserved, “often eliminating novelties which undermine it” (Bernath and Vidal, 2007) [1] . Research does not discover the unknown, but rather “a strenuous and devoted attempt to force nature into the conceptual boxes supplied by professional education” that is based on these theories (Kunt, 1996) [2] .

Theories imply a systematic ordering of concepts, principles and laws about the object of inquiry of a particular factual science and are mainly of two kinds. One is concerned with understanding, which is descriptive and analytical, and the other is with explanation and prediction, transcending the facts. A theory is a conceptual unit of facts, assumptions and hypotheses. This unit shows how facts are subordinated to general principles or laws. A scientific theory must be consistent with the facts and verified by experiments or observations. Theories focus on one selected aspect of the object according to the goals of a particular factual science (Bernath and Vidal, 2007) [1] .

A set of theories are the foundation of the normal science that “means research firmly based upon one or more past scientific achievements, achievements that some particular scientific communities acknowledge for a time as supplying the foundation for its further practice”. These achievements are called paradigms. A paradigm is essential to scientific inquiry—“no natural history can be interpreted in the absence of at least some implicit bodies of intertwined theoretical and methodological belief that permits selection, evaluation, and criticism” (Kunt, 1996) [2] .

Paradigms have a cycle of life. They emerge from pre-paradigmatic theories in competition. “To be accepted as a paradigm, a theory must seem to be better than its competitors, but it need not, and in fact never does, explain all the facts with which it can be confronted” (Kunt, 1996) [2] . When a new paradigm is adopted by the scientists of a particular science the previous paradigm and/or the other pre-paradigms disappear. The paradigm transforms groups into a profession or, at least, a discipline. And from this, the formation of specialised journals, foundation of professional bodies and a claim to a special place in academe follow (Pajares, 2012) [3] . The paradigm becomes the normal science that through the scientific inquiry it actualizes and increases. But, no effort is made to discover anomalies. When anomalies pop up, they are usually discarded or ignored. Anomalies are usually not even noticed and no effort is made to invent a new theory (and there’s no tolerance for those who try) (Pajares, 2012) [3] . Research results during a long time are the refinement of the vocabulary and concepts, development new technologies, the construction of complex equipment, and the realization of highly precise experiments and sophisticated methodological observation. This professionalisation leads to immense restriction of the scientist’s vision, rigid science, resistance to paradigm change, and a detail of information and precision of the observation-theory match that can be achieved in no other way. New and refined methods and instruments result in greater precision and understanding of the paradigm (Pajares, 2012) [3] . But while the governed paradigm-based research is “an attempt to force nature into the pre-formed and relatively inflexible box that the paradigm supplies” (Kunt, 1996) [2] , and through normal science, the paradigm is self-perpetual. Paradoxically, with the cumulative development during a long time of the paradigm, researchers can recognise that something has gone wrong. Consequently, anomalies appear. There are three ways: through discovery—novelty of fact; by invention—novelty of theory; or by reunderstanding theory. Consequently, anomalies appear. Discovery begins with the awareness of anomaly—the recognition that nature has violated the paradigm-induced expectations that govern normal science. The recognition of anomalies results in crisis that is a necessary condition for the emergence of novel theory and for paradigm change (Pajares, 2012) [3] . When crisis scientists confronted with anomalies or took a different attitude toward existing paradigms and therefore the nature, their research changes. The proliferation of articulations in competition, the disposal for rehearse it all, the explicit discontent, the recourse to philosophy and the debate on the foundations, are symptoms of a transition of the normal investigation to non-ordinary (Kunt, 1996) [2] . Theoretical alternatives are made, which initially can be speculative theories. Crisis is the essential tension implicit in scientific research. In responding to this crisis, scientists generally do not renounce the paradigm that has led them into crisis. Rather, they devise usually numerous articulations and ad hoc modifications of their theory in order to eliminate any apparent conflict. All crises are closed in one of three ways. (1) Normal science proves able to handle the crisis-provoking problem and all return to “normal.” (2) The problem resists and is labelled, but it is perceived as resulting from the field’s failure to possess the necessary tools with which to solve it, and so scientists set it aside for a future generation with more developed tools. (3) A new candidate for paradigm emerges, and a battle over its acceptance ensues (Pajares, 2012) [3] . Once it has achieved the status of paradigm, a paradigm is declared invalid only if an alternate candidate is available to take its place. Because there is no such thing as research in the absence of a paradigm, to reject one paradigm without simultaneously substituting another is to reject science itself. Transition from a paradigm in crisis to a new one from which a new tradition of normal science emerges is not a cumulative process. It is a reconstruction of the field from new fundamentals. This reconstruction changes some of the field’s foundational theoretical generalisations. It changes methods and applications. It alters the rules (Pajares, 2012) [3] . The result is a scientific revolution that is a non-cumulative developmental episode in which an older paradigm is replaced in whole or in part by an incompatible new one (Pajares, 2012) [3] , i.e., a profound change (Bachelard, 2010) [4] . The paradigm change is complete when the paradigm has been adjusted so that the anomalous become the expected. The result is that the scientist is able “to see nature in a different way” (Kunt, 1996) [2] . The scientific progress occurs only through scientific revolutions. Successive transition from one paradigm to another vía of a revolution is the usual pattern of development of a mature science (Kunt, 1996) [2] .

In the science of physics, according to mechanic, since the epoch of Aristotle’s pre-paradigm, there have been the revolutions of Galilei-Newton and Einstein. “The mechanics of Isaac Newton in the 17th century, the special relativity and the general relativity in the twentieth century, were paradigms to represent and understand the universe” (Jaoude, 2013) [5] . In Aristotle’s physics, the motion was caused by force, “there was absolute time, absolute space and an absolute rest frame, provided by earth” (Ashtekar, 2006) [6] .

Newton introduced the classical mechanics paradigm applied to the motion in the macroscopic world. This paradigm is based on principle of least action, determinism and law of inertia of Galilei. The inertial motion is not caused by force but by absence of force. The gravitational motion is caused by force. The “time was sill represented by a 1-dimensional continuum and was absolute, the same for all observers. All simultaneous events constituted the 3-dimensional spatial continuum. But there was no absolute rest frame. Thanks to the lessons learned from Copernicus, earth was removed from its hitherto privileged status. Galilean relativity was made mathematically precise and all inertial observers were put on the same physical footing” (Ashtekar, 2006) [6] , according to Galilei’s transformation.

Einstein introduced the relativistic mechanics as a new paradigm which generalizes the principle of inertial motion to all motion, including the gravitational motion. “Einstein revolutionized the notions of space and time, first through special relativity and then, a decade later, through general relativity” (Ashtekar, 2006) [6] . “Modify fixed concepts (inertial mass, gravitational mass and gravity) in order to fit a series of new experimental facts into a coherent world ruled by an “improved” paradigm: the relative mechanics paradigm” (Bass, 2002) [7] . “General relativity due to the numerous experiments made, especially after 1960, all with results impressively accurate to favour of this theory, to its conceptual integration with its antecedent the special relativity and the numerous theories derived in physics, astronomy and cosmology truly the relativity is the current physics paradigm” (Guillen, 2013) [8] . “A new, better model emerged and with it new kinematics, was called special relativity”. Time lost is absolute standing. Only the 4-dimensional space-time continuum had an absolute meaning. Space-time distances between events are well defined but time intervals or spatial distances between them depend on the state of motion of the observer, i.e., of the choice of a reference frame” (Ashtekar, 2006) [6] . In general, relativity of the action of a free particle is proportional to the length traveled by the particle along a geodesic’ space and time fusing to form a 4-dimensional continuum. The geometry of this continuum is curved and the amount of curvature in a region encodes the strength of the gravitational field there. Space-time is not an inert entity. It acts on matter and can be acted upon”. “This is a profound paradigm shift. Since all physical systems reside in space and time” (Ashtekar, 2006) [6] , the action of a free particle is proportional to the length traveled by the particle along a geodesic. Thus, classical mechanics is extended to particles traveling at speeds close to c, including electromagnetism in spacial relativity and gravity, in general relativity, beyond the reach of Galilei’s relativity.

Mainly the differences, between the Newton’s paradigm and the relativistic paradigm, in the special relativity are the discoveries reached, with subsequent scientific development to Newton, in laws of motion in the inertial systems; while, in the general relativity, the geometrization of gravity, a force, is in the case de Newton. The mechanic laws, of Galilei-Newton, are apply only to the inertial systems, without including the privileged inertial system of Lorentz, i.e. only systems in that electromagnetic laws are valid, while in the special relativity the laws of the nature are valid in all the inertial systems. Therefore, it includes Lorentz’s system, and also the law of the maximun limit of speed and speed constant of light in vacuum, and for this reason between inertial systems, to calculate the change of coordinates, it uses the transformation of Lorentz, while in Newton, it uses the transformation of Galilei, since it does not include such effects of the speed of light, that in the special relativity implies, the relativity of time and space, while in Newton, the time and space are absolute. On the other hand, in general relativity is generalized by the inertial motion of the plane space, to the curved spacetime. Thus Einstein identifies the functions g_uv with the gravitational field and this field with gravity and, since the functions g_uv express geometric relations between events, then he geometrizes gravity, i.e. consequence of the method based on the principle of equivalence between the inertial system, the accelerated system and the gravitatory system applied in the differential tensorial geometry used by Einstein.

Relativistic mechanics coexists practically since its foundation with, its main external anomaly, quantum mechanics, is applied in the scale of the microscopic world, in the context of classical mechanic, quantizing the action on the order of the Planck constant, that is, its elemental unit, and responding to Schrödinger’s wave function. Quantum mechanics is governed by the wave-particle duality of energy and matter and Eisenberg’s uncertainty principle. Relativistic mechanics with the relativistic quantum mechanics has succeeded in developing quantum mechanics applied with the special relativity, but not with general relativity. Thus, the relativistic physics lost determinism and quantum theory lost the action quantized. But, relativistic quantum mechanics is only an approximation to relativistic quantum field theory in which particles are interpreted as field quanta and of course this theory can describe creation and annihilation of particles, where its amount changes (Messiah, 1981) [9] . On the other hand, the result of applying general relativity into quantum theory is the quantum gravity, a critical external anomaly in relativistic physics. While general relativity is a geometric theory on gravity of the inertial motion in an elliptically curved spacetime in change, quantum gravity is a physical theory on gravity, of the interaction forces between the virtual graviton and all other quants, included the same virtual graviton. “Today scientists describe the universe in terms of two basic partial theories―the general theory of relativity and quantum mechanics”. “Unfortunately, however, these two theories are known to be inconsistent with each other―they both cannot be correct. One of the major endeavors in physics today”, is the search for a new theory that will incorporates them both―a quantum theory of gravity” (Hawking, 2001) [10] .

Relativistic mechanics has other anomalies yet more profound anomalies, since those are one structural anomaly and internal anomalies, from its conception. Here, in this paper, we analyze the structural anomaly and two internal anomalies with the goal of proposing the change of this paradigm.

2. Relativistic Paradigm without Epistemological Break

The fundamental component of relativistic paradigm, i.e. general relativity is an application of Galilean’s relativistic theory on the inertial motion in euclidean spacetime plane, to riemannian spacetime, elliptically curved. This is the conclusion of the author, through reread the general relativity theory since the perspective of the history of the science and the philosophy of the science.

The unique geometry known in the time of Galilei was Euclid’s geometry, from year 300 BC, that studies the geometric properties of plane space, i.e., with a curvature equal to 0, where the sum of the angles of a triangle is equal to 180 grades, based in five axioms, considered as weak the fifth, on the parallel lines: for a point outside a line, only it can draw a line parallel to the given line. Euclidean geometry initially restricted to a space, of two orthogonal dimensions, compound by infinite points and lines, that is represented in a cartesian coordinates system, where a point is determined by real numbers x₁, x₂ was applied to three orthogonal dimensions x₁, x₂, x₃ and generalized to a space n-dimensional Rⁿ metric (η_μν), where metric allows one to define and compute the length of straight lines on the Rⁿ. Thus, a space is a geometric object, used to determine and to measures the shape, size, angle, distance and relative position, direction and sense of objects or events.

Previous to formulation of law of the inertia, Galilei did three experiments inside of a euclidean space R³. Two experiments were done on a body of shape pyramidal, therefore, with an inclined surface and the third experiment on the surface of a plane body. In the first experiment established that a sphere was moving uniformly accelerated when descended and in the second experiment animated with an initial speed, when ascended the sphere was decelerated uniformly. Galilei induced that on plane, the sphere would be in rest when its initial speed equal 0, or with rectilinear uniforme motion whether its initial speed greater than 0. However, when Galilei realized its third experiment on plane, animated with an initial speed, the sphere was decelerated uniformly. Then, Galilei discovered that was due to the friction force between the surface of plane and sphere. Course, whether it eliminates this friction, sphere would move rectilinearly with uniform speed. Through this inductive experimental method Galilei formulated the inertia principle: The vis insita, or innate force of matter, is a power of resisting by which everybody, as much as in it lies, endeavours to preserve its present state, whether it be of rest or of moving uniformly forward in a straight line (Newton, 1846) [11] . Thus, Galileo refuted conception of Aristotle on motion, since motion is not caused by force as he said, but by absence of force. Aristotle believed that bodies would move only while it is pushing or pulling them, i.e., moved by a mover. “Everything that is in motion must be moved by something”. “The mover too is moved, as has been said—every mover, that is, which is capable of motion, and whose immobility is rest—when a thing is subject to motion its immobility is rest. To act on the movable as such is just to move it. But this it does by contact, so that at the same time it is also acted on. Hence we can define motion as the fulfillment of the movable qua movable, the cause of the attribute being contact with what can move so that the mover is also acted on. Now since wherever there is a movement, its motion always acts upon something, is always in something, and always extends to something (by “is always in something” I mean that it occupies a time: and by “extends to something” I mean that it involves the traversing of a certain amount of distance: for at any moment when a thing is causing motion, it also has caused motion, so that there must always be a certain amount of distance that has been traversed and a certain amount of time that has been occupied)”. “Can never be motion of mover and moved, because there cannot be motion of motion” (Aristotle, 1930) [12] .

The rectilinear uniform motion arises of a geometric property of plane space, i.e. the plane space tells matter how to move, exactly the plane space says to matter move it rectilinearly, but it does not cause motion, i.e., change from rest into motion. Since, whether a body has a initial speed is because was caused by action of a previous force that was applied to it; a force that acted by contact, at exact moment that such force communicated to body a determined speed, i.e., the effect of an instantaneous action applied by contact; when that force ceased the speed is maintained by inertia; however, whether exists a friction force on body is need a mover to maintain motion, therefore, in that sense, Aristotle is correct. Surely, the force does not cause motion, but force is cause of change of speed, for example, it is need a force to animate a body, initially with speed equal to 0, i.e. in rest, for that it moves with a speed greater than 0. Also, the inertial force that arises when the inertial motion is altered or is ended is reaction force to a action force that was applied to a body in inertial motion, that can put it out its rectilinear way, in any case, accelerate it. Understand correctly true difference between thought on motion of Aristotle and Galilei is source frequently of lethal mistake. Rigorously, the principle of inertia of Galilei establishes that a body maintains its state of rest or motion while a force does not act, and in the arena of a plane space, its geometric property it determines that a body it moves rectilinearly in the direction and sense of the force that put out body of rest; thus is need a force to initiate body motion and a mover to maintain to body moving when on it acts a force of reaction, as in form approximated Aristotle said.

Galilei established, through their experiments, the principle of relativity, which declares the motion is relative because always is necessary refer the mobile body, inside a space system coordinates, called inertial frame of reference, to other where there is an observer. Thus, there are an infinite number of inertial frames. Only in this arena is possible determine that a body is moving, since, whether a body is traveling at uniform speed there is not any experiment able to determine whether the body is moving or in rest. Therefore, the speed and the states of rest or motion are relative (However, the author, of this work, has proved the absolute motion (Guillen, Sept 2013)) [13] . To determine the motion is used the transformation of Galileo that expresses the coordinates of an inertial frame of reference, i.e., at R³, of a body or, at R⁴ metric (η_μν) of an event, respect to the coordinates of other inertial frame, doing possible in this last inertial frame establish whether the body or event is in relative state of motion or spatial rest, also measure its relative speed. This transformation has the property of that the laws of motion are the same, in all the inertial frames, property known as principle of invariance.

In summary, the theory of Galilei is a mechanic physics theory, whose bodies and events occurs inside plane space of geometry of Euclides, governed by principles of inertia, invariance, rectilinear uniform motion, trajectory as a geometric property of a plane space and galilean transformation.

In the decade of 1830, it discovered two options to Euclid’s geometry, consequence of the affine geometry that studies parallel lines, and it enabled change the fifth postulate, resulting the called non-Euclidean geometries. These are:

• Hyperbolic geometry, with curvature negative, where the sum of the angles of a triangle is less than 180 grades, generated mainly by Friedrich Gauss, Nikolái Lobachevski and János Bolyai, through change the fifth postulate of Euclid’s geometry by: given a line l and a point P not on l, then there are two distinct lines through P that are parallel to l (Ross, 1990) [14] .

• Elliptical geometry, with curvature positive, where the sum of the angles of a triangle is greater than 180 grades, generated by Friedrich Gauss for sphere in two dimensions, and generalized for sphere in n-dimensions by Bernhard Riemann, through change the fifth postulate of the Euclid’s geometry by: given a line l and a point p outside l, there exists no line parallel to l passing through p.

• Here, we will update the Galilei’s physics applied to elliptical geometry, i.e., the Galilei’s mechanic at the curved positively Riemann’s space in 4 dimensions. Thus:

• Principle of inertia: all body in rest or in geodesic motion will stay in such state, while body is free of force, inside of an inertial frame.

• The trajectory of the motion of a body will be uniformly positive curved and it arises of property geometric of the space.

• Principles of relativity and invariance are conserved although generalized to all frames. According to the generalized invariance the laws of physics are expressed in same form in all coordinate systems; intrinsic property of the tensors that are independent of any chosen coordinate system.

As it observes Galilei’s physics when is applied to elliptical geometry, coincides in the essential with general relativity. Too, whether in Newton’s physics the gravitational motion is explained by the geodesic motion, Galilei-Newton’s physics it geometrizes. Since this perspective general relativity is resulted of the development of the relativity of Galilei. In particular, the generalization of the principle of inertia of the plane space to the positively curved space (Guillen, 2006; Petkov, 2012) [15] [16] .

In the elliptical geometry the straight line is equivalent to the geodesic that is defined as a curve such that a point moving along the curve with the velocity of constant magnitude (i.e. the velocity can change its direction but not its magnitude) has the acceleration vector perpendicular to the given surface, i.e. the acceleration component tangent to the given surface is zero (Pokorny, 2012) [17] . General relativity incorporates a number of basic principles that correlate spacetime structure with physical objects and processes. Among them is geodesic principle: free massive point particles traverse timelike geodesics. One can think of it as a relativistic version of Newton’s first law of motion (Malament, 2009) [18] . By the geodesic hypothesis in general relativity, the assumption that the worldline of a free particle is a timelike geodesic in spacetime is a natural generalization of Newton’s first law, that is, a mere extension of Galileo’s law of inertia to curved spacetime. This means that in general relativity a particle, whose worldline is geodesic, is a free particle which moves by inertia (Petkov, 2012) [16] .

In consequence, with relativistic paradigm, based in general relativity, is there is a new paradigm? yes, in sense of Kunt but without the epistemologic rupture of Althusser, which implies irreversibility in the paradigm shift, because it no longer supports backtracking, it is established a new notion, without return point (Gassmann, 2013) [19] , emergence of unprecedented concepts of a new scientific problem (Balibar, 2004) [20] . Since, in general relativity whether there is reversibility, with respect to Galilei-Newton’s paradigm, as we have analized, i.e., in Galilei’s mechanic potentially resides general relativity. Then, in the relativist paradigm does not exist epistemologic rupture. However, often it believes otherwise.

3. Estructural Anomaly

In Galilei-Newton, the science of the physics works its object of study: the matter and energy and their relations through of the process of production of a factual science. Thus, through theoretical and experimental tools transforms the model that is its object of work, by scientific praxis whose peculiarity is that unlike an economic production is not to achieve the material form previously exists and pursued in a specific production of goods or services, but to test hypotheses, making methodologically observations and experiments for produce an new knowledge or improving an existing one (Althusser, 1967) [21] in the cumulative process of normal science, inside of the current paradigm.

In the Galilei-Newton’s physics is used a scene to locate its object of study; these are the inertial frames defined by coordinates. They are geometric objects that its study corresponds to the formal science of the geometry. The inertial frame leads to structural anomaly of Galilei-Newton’s paradigm due to that is not only the frame of the mechanic, also determines the trajectory of motion and thus it is strongly linked to spacetime, a concept no defined yet by physics, but by metaphysics (Guillen, Dec 2013) [8] . This anomaly is preserved when the inertial frame of the plane spacetime is generalized to the positively curved spacetime. In consequence, via general relativity, the relativistic paradigm reproduces anomaly of the inertial frame formulated as geodesic frame. In addition, critically aggravates this structural anomaly, when gravity is defined as the positive curvature of spacetime, resulting from the geodesic frame, in Galilei-Newton a physical phenomenon. The intrinsic geometry of positively curved spacetime M₄ υ g_uv, since, has not a constant metric tensor between two events (Euclides’s spacetime, whether), therefore, the shortest curve is a geodesic, that is equivalent to the straight line of a Euclidean coordinate system.

General relativity is based conceptually in the equivalence between inertial mass and gravitational mass, that Galilei discovered, and that was proved in the Eötvös experiment, and in two thinking experiments that were realized in the called Einstein’s box, in Minkowski’s spacetime, of the special relativity, that is a pseudo-euclidean space R^4, with the property that speed of a massive particle or a body must be less than speed of electromagnetic wave in the vacuum c, this is an intrinsec geometric property of the interval(s) between two events, this interval can be: space-like whether s² > 0, time-like whether s² < 0 and light-like whether s² = 0; surely, the only interval possible for a massive particle or a body is space-like. In the first experiment the Einstein’s box is in free fallen, but for an interior observer all happen as if its frame is an inertial frame of Galilei, although restricted to little speeds while to an exterior observer is a gravitational frame, this experiment was tested in artificial satellites orbiting the Earth, the result is the principle of equivalence between an inertial frame and a gravitational frame. In the second experiment the Einstein’s box is uniformly accelerated according value g, in the orthogonal direction to soil and in up sense, but for an interior observer all happen as whether its frame is a gravitational frame while to an exterior observer is an accelerated uniformly frame, in addition, the exterior observer discovers that light traces a positively curved trajectory that the interior observer explains as effect of its curved spacetime, the result is the principle of equivalence between an uniformly accelerated frame and a gravitational frame. To Einstein as gravitational frame is equivalent to inertial frame and equivalent to uniformly accelerated frame, also uniformly accelerated frame equivalent to positively curved spacetime then gravity is caused by positively curved spacetime since the uniform acceleration suffered by the bodies submitted to the action of gravity arises of this last equivalence: if plane spacetime is curved by acceleration then curved spacetime produces acceleration. Thus, Einstein told, to Newton: all the reference frames are equivalents. And like Galilei told on motion, to Aristotle;  Einstein told, to Newton: gravity is not a force but accelerated uniformly motion caused by positively curved spacetime, based in the wrong interpretation of Galilei’s principle.

In general relativity, the phenomenon of gravity is removed from the physics and it is put in arena of geometry. The tensor of order 4 (M₄), geometric object represented the positively curved spacetime, metric (g_uv), this metric allows one to define and compute the length of positively curved lines on M₄, it becomes the model same of gravity, since gravity is the same frame where the physical phenomenon occurs. Thus, the theory on gravity is presented in the intrinsic language and logic of the formal science of the mathematic, in the complex scene of differential geometry that uses the techniques of the linear and multilinear algebra, differential calculus and integral calculus of tensors of order 4. A mathematic whose variables are geometric objects in 4 dimensions, very difficult understand and operate, whose concepts replace to the concepts of the physical theory and they block the intellectual access to the anomalies of a physical theory geometrized. Such mathematical concepts are very obscure concepts as the curvature tensor of a Riemann manifold that “is a little monster of multilinear algebra whose complete geometrical meaning remains obscure” (Gromov, 1994) [22] .

4. From Galilei, Einstein Arrived to General Relativity

Surely, the discovery of non euclid’s geometries does not drive necessarily to the geometrization of the physics as happened with general relativity, because the application of a physics theory to an inertial frame, itself is an mathematical exercise, which only is important always that it can use in the description of a physical phenomenon. Hyperbolical geometry or elliptical geometry applied  to Galilei’s mechanic only changes the inertial trajectory of the motion of a body in a negatively curved line, or in a positively curved line. The election of any of two options only is relevant whether exist in the nature, a inertial motion corresponding that necessarily it will must test. In effect, gravitational motion traces a curved positively trajectory, which does possible explain, this trajectory using elliptical geometry applied to the gravitational motion. This does not mean, that the gravitational motion has as cause the elliptical geometry of the spacetime, similarly that the Euclid’s plane geometry of the spacetime is not cause of motion of a body that need a force to leave its state of rest, but, whether that a body in inertial motion traces a rectilinear trajectory at a plane space or a geodesic at a curved spacetime.

Einstein did not the previous reflections. He elaborated general relativity using the principle of equivalence between an accelerated system and a gravitational system. As bridge, he used the principle of equivalence between an inertial system, and a gravitational system, based in the equivalence between inertial mass and gravitational mass, experimentally established.

Thus, Einstein applied the double principle of equivalence and he established that inside of an infinitesimal lapse of the spacetime, since in it its variation of gravity can be considered null, a inertial frame is equivalent to a gravitational frame as also an accelerated uniformly frame is equivalent to a gravitational frame.

Einstein considered the simple case of a transformation from an inertial frame of special relativity to a frame in uniform rectilinear acceleration. In the accelerated frame of reference a homogeneous inertial field arises. Because of the key empirical fact of the equality of inertial and gravitational mass, Einstein was able to identify this field as a gravitational field (Norton, 1993) [23] .

From the principle of equivalence, the inertial frame, the accelerated uniform frame and the gravitational frame are equivalents, i.e., kinematics produces inertia, acceleration or gravity according the coordinates of a particular observer, therefore inertia, acceleration and gravity are relative kinematics phenomena depending of the system of coordinates of the observer, absolutely a accident geometric of the spacetime, relative to the configuration geometric of spacetime of a particular observer. The change from the inertial frame to gravitational frame or vice versa, or from the accelerated frame to the gravitational frame or vice versa, is a simple question of change of coordinates, i.e., technically, a geometric manipulation of spacetime.

Einstein started with the invariant interval of Minkowski in differential form

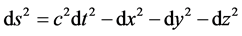(1)

where (x, y, z, t) are the space and time coordinates of an inertial frame of reference in a Minkowski spacetime. Transforming to arbitrary coordinates x_u for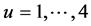, becomes

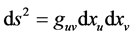(2)

where the magnitudes g₁₁, etc., have values which vary with the position in the continuum.

Einstein employed his principle of equivalence to interpret the matrix of quantities g_uv that had arisen with the introduction of arbitrary coordinates. In the special case of the principle, the transformation from (1) to (2) is from an inertial coordinate system to a uniformly accelerated coordinate system. In that case, the matrix of coefficients g_uv reduces to that of (1), except that c now is a function of the coordinates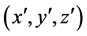. That is, (2) becomes

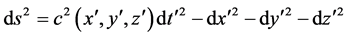(3)

According to the principle of equivalence, the presence of a gravitational field was the only difference between the spacetime of (3) and that of special relativity (1). Therefore Einstein interpreted the coordinate dependent c of (3) as representing a gravitational field and, more generally, the g_uv of (2) as representing a gravitational field (Norton, 1993) [23] .

From principle of equivalence, inertia and gravity are identical in essence. From this and from the results of the special theory of relativity, it follows necessarily that the symmetric fundamental tensor (g_uv) determines the metric properties of space, the inertial relations of bodies in it, as well as gravitational effects (Norton, 1993) [23] .

As the gravitational field is a simple consequence of a new expression of Minkowski coordinates and these a new expression of cartesian coordinates, the gravitational field does not imply energy-momentum.

However, out of limit, of the infinitesimal lapse, the gravitational field has the full properties of a curve geometry, from the Gaussian coordinate system according (2), that is a logical generalization of the cartesian frame. Thus, the spacetime continuum of the general theory of relativity is not a Euclidean continuum. We start off on a consideration of a Galilean domain, i.e. a domain in which there is no gravitational field relative to the Galilean reference-body K. The behaviour of measuring -rods and clocks with reference to K is known from the special theory of relativity, likewise the behaviour of isolated material points; the latter move uniformly and in straight lines. Now let us refer this domain to a random Gauss coordinate system or to a mollusc as reference-body K1. Then with respect to K1 there is a gravitational field G. We learn the behaviour of measuring-rods and clocks and also of freely-moving material points with reference to K1 simply by mathematical transformation. We interpret this behaviour as he behaviour of measuring-rods, clocks and material points under the influence of the gravitational field G. Here upon we introduce a hypothesis: that the influence of the gravitational field on measuring rods, clocks and freely-moving material points continues to take place according to the same laws, even in the case where the prevailing gravitational field is not derivable from the Galileian special case, simply by means of a transformation of coordinates. According to the general principle of relativity, the space-time continuum cannot be regarded as a Euclidean one. We refer the four dimensional spacetime continuum in an arbitrary manner to Gauss coordinates (Einstein, 1920) [24] .

The gravitational field is at best a geometric not a physical field (Minkowski, 2012 [25] . We denote everything but the gravitational field as matter. Our use the word therefore includes not only matter in the ordinary sense, but the electromagnetic field as well (Einstein, 1997) [26] . When gravitational phenomena are adequately modelled by the spacetime curvature it is evident that the gravitational field is not something physically real, that is, it is not a physical entity. It is a geometric field (Petkov, 2012) [16] . We have seen how Einstein defined the gravitational field to be identical to the so-called metric tensor g_uv used by Riemann to describe the geometry of a curved space. Einstein’s minimalist adoption of g_uv as the embodiment of the gravitational field was significant and has far-reaching ramifications (Odenwald, 2009) [27] . This complete reduction to kinematics yields a purely geometric field of gravitation (composed of metric, curvature, geodesic lines) and a theory which is fully consistent with the original guiding principle of equivalence (Dalton, 1997) [28] .

Thus, Einstein geometrized the phenomenon of gravity, since he does not only explain the trajectory of the gravitational motion, but also, the gravitational acceleration and the atraction between particles and in general between the bodies by the geodesic motion, in the positively curved spacetime, an metaphysical entity. General relativity as geometric phenomenon, and as phenomenon of the metaphysic spacetime, structurally is based in a critical and complex anomaly, partially inherited of Galileo-Newton and completed by Einstein.

5. Internal Anomalies

In general relativity, the matter-energy acts on spacetime and spacetime acts on matter-energy, in particular: matter tells space-time how to bend and space-time tells matter how to move (Wheeler, 1990) [29] . This symmetric relation between spacetime and matter puts in relation to two entities that are contraries, since while matter-energy is an physical entity, spacetime is a geometrical entity, according to super substantivalism, the best conception on it, a metaphysical entity (Grant, 2013) [30] . In addition, Einstein pushed physics to abyss of metaphysics when he explained the phenomenon of gravity as the consequence of the curvature of spacetime (Guillen, Dec 2013) [8] . In terms of the current relativistic paradigm in this work, we have conceptualized both, i.e. the metaphysical spacetime and the metaphysical phenomenon of the gravity as the critical complex structural anomaly, that produces the internal two anomalies, of this paradigm, that are analized in this work. These anomalies arise of the processes concerning to:

• Matter-energy curves spacetime. General relativity defines and determines such process, only operationally, through of the Einstein’s field equations:

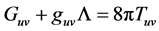
where G_uv is Einstein tensor formed from the second derivatives of the metric tensor, metric tensor g_uv that describes spacetime curvature, Λ is the cosmological constant and T_uv the distribution of mass-energy.

But, it is a mystery as a physical entity, matter-energy, can curve a metaphysical entity, spacetime, also with positive curvature, although it could be with negative curvature.

• Curvature of spacetime puts in accelerated motion, to a body in rest. General relativity only operationally determines this process through of the geodesic equation (Einstein, 1922) [31] :

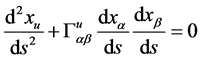
But, it is a mystery as a metaphysical entity, spacetime, can put at accelerated motion to a physical entity, matter-energy, yet worst that spacetime, that lacks of energy-momentum (Logunov, 1989) [32] , can put at accelerated motion, to a body in rest (Van Flandern, 2004) [33] .

In the special relativity, the particles or bodies always are in motion, although they can be in rest, respect to space; in such case, to put them in motion is need apply a force. In the general relativity the particles and bodies always are accelerating, yet when they are in rest, because Einstein established the equivalence between positively curved spacetime and accelerated spacetime. Thus, if a spacetime is positively curved, then the motion of particles or bodies is accelerating. But, the Earth is positively curved, its geodesics converge at the north and south poles, however, particles on geodesics are not observed that they are accelerating. Although, it says that Earth is not spacetime.  Will be that Earth has not spacetime?

6. Conclusions

The result, of this work, is that the current relativistic paradigm is the development of the classical paradigm, without epistemological break, when conserving the Newton’s spacetime as a geometric container, with a real existence, of matter-energy, however, now as dynamic actor. Also, generalizing the principle of inertia of Galilei of the plane space, to positively curved spacetime, and by this via, it geometrizes physics, when it is explained the phenomenon of gravity as the effect of the positive curvature of the spacetime and in summary, our conclusions are:

• The general relativity structurally is based on the complex anomaly of the metaphysical spacetime and the replacement of physics by metaphysics due to that gravity is a metaphysical phenomenon.

• The general relativity presents a first internal anomaly by no given conceptual explanation as physical matter-energy curve metaphysical spacetime.

• The general relativity presents other second internal anomaly by no given conceptual explanation as the curvature. A simple geometric property of metaphysical spacetime can put in accelerated motion, to the physical particles and physical bodies, yet in rest.

Due to the previous anomalies, it is necessary to have a new paradigm.

References