Journal of Modern Physics
Vol.4 No.12(2013), Article ID:40915,7 pages DOI:10.4236/jmp.2013.412197
Atom-Field Entanglement inside a Cylindrical Nanotube
Department of Physics, Taibah University, Medina, KSA
Email: alawfi99@hotmail.com
Copyright © 2013 S. Al-Awfi. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received October 5, 2013; revised November 3, 2013; accepted November 28, 2013
Keywords: Atomic Inversion; Maximal Entangled States; Degree of Entanglement
ABSTRACT
This work presents the entanglement between an electromagnetic field and two-level atom situated inside a quantum optical system. Our optical model is based on cylindrical tube with a hole diameter of the order of nanoscale which leads to that only the lowest order mode can exist. Numbers of the statistical features of effective Hamiltonian such as the temporal evolution of the atomic inversion and the von Neumann entropy are evaluated. We have evaluated the atomic inversion and we demonstrate that the atom stills in maximal entangled state when the radius of tube a is large. We have used the von Neumann entropy to measure the degree of that entanglement. The results illustrate that the effect of the radius of tube a changes the quasi-period of the field entropy and therefore the entanglement process.
1. Introduction
Entanglement process is one of the most mystifying properties of quantum optics. It is the key constituent for a lot of experiments in quantum communication and information processes [1-3]. Particularly for future applications similar to quantum networks or the quantum repeater, it is required to achieve entanglement as well between separated quantum processors. Because entanglement between different quantum particles such as atoms and photons forms the interface between atomic quantum memories and photonic quantum communication channels, lastly allowing the distribution of quantum information over arbitrary distances [4-7].
This work explains the generation and confirmation of an entangled state between a single neutral atom and a single quantize cavity-mode at a wavelength suitable for long distance information transport [8,9]. For this objective, we store a single atom in an optical dipole trap within cylindrical nanotube. Recently, advances in nanofabrication technology as well as in the production of intense tunable lasers, have refreshed activity in atom optics in nanoscale region. Both have led to significant progress in the control of neutral atoms using laser light [10,11]. The manipulating atoms through cylindrical tube become an important sub-field of nanoscale studies. Because it can occur easily and efficiently in a manner similar to the propagation of light in the fiber optics. This has been a target of extensive theoretical and experimental studies [12-14].
In this work, we examine the entanglement between an electromagnetic field and atom situated inside a cylindrical nanotube. We concentrate here on cylindrical tubes with a circular cross section which are more common in practice and they have featured more prominently in recent applications than other systems [15-17]. However, as far as we know, the entanglement between atom and electromagnetic field inside cylindrical tubes in such a practical system has not previously been investigated. It is the primary purpose of this paper to examine the essential ingredients of the theory leading to the description of entanglement between atom and electromagnetic field inside cylindrical nanotube. Such a study should provide the initial steps towards a more comprehensive understanding of the nature of entanglement process within confinement systems in general.
The paper is organized as follows. In Section 2, we introduce the effective Hamiltonian for an atom coupled to the quantized field within a cylindrical nanotube. By using the evolution operator, the expression of the wave function at any time  is obtained in Section 3. Section 4 is devoted to a discussion of the atomic inversion and we show that it exhibits collapses and revivals for short time intervals. In Section 5, we write the mathematical form for the quantum field entropy and we use numerical computations to examine the effect of the radius of the tube on the evolution of the field entropy and hence entanglement between the atom and the field. Finally, Section 6 contains the conclusions.
is obtained in Section 3. Section 4 is devoted to a discussion of the atomic inversion and we show that it exhibits collapses and revivals for short time intervals. In Section 5, we write the mathematical form for the quantum field entropy and we use numerical computations to examine the effect of the radius of the tube on the evolution of the field entropy and hence entanglement between the atom and the field. Finally, Section 6 contains the conclusions.
2. Effective Hamiltonian
The cylindrical tube is depicted in Figure 1. As shown in this figure,  is the radius, the tube is infinite in length and the longitudinal spatial variation is along the
is the radius, the tube is infinite in length and the longitudinal spatial variation is along the , coincident with the straight line
, coincident with the straight line . The walls of the tube are perfectly conducting excluding all electromagnetic fields from their interior. The standard electromagnetic boundary conditions apply such that the tangential components of the electric field vector and the magnetic field vector must vanish at every point on the cylinder surface. The optical system consists of an atom of mass
. The walls of the tube are perfectly conducting excluding all electromagnetic fields from their interior. The standard electromagnetic boundary conditions apply such that the tangential components of the electric field vector and the magnetic field vector must vanish at every point on the cylinder surface. The optical system consists of an atom of mass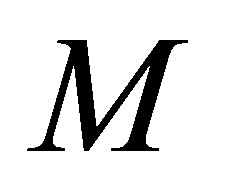 , characterized by its electric dipole moment
, characterized by its electric dipole moment , of oscillation frequency
, of oscillation frequency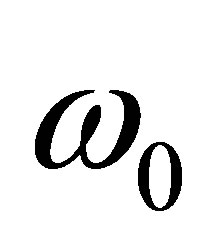 , interacting with the electromagnetic field. The effective Hamiltonian can be written as:
, interacting with the electromagnetic field. The effective Hamiltonian can be written as:
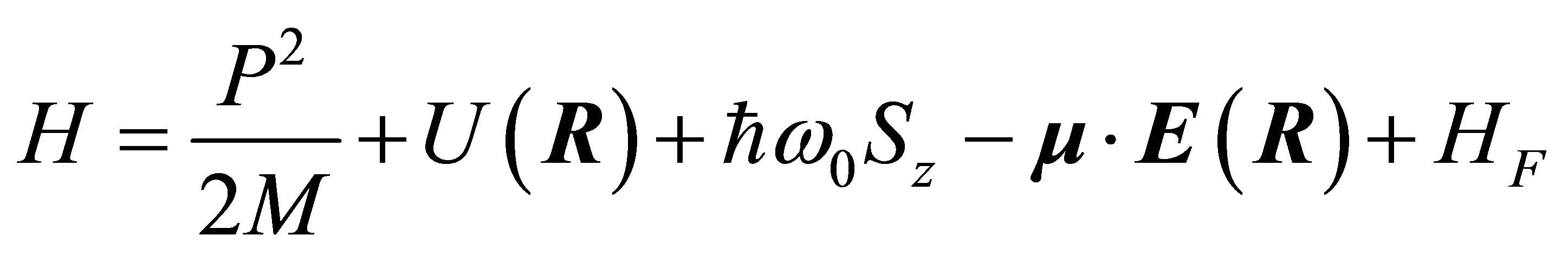 (1)
(1)
where  and
and  are the momentum and position vectors of the atomic centre of mass, which is assumed to be subject to a general potential
are the momentum and position vectors of the atomic centre of mass, which is assumed to be subject to a general potential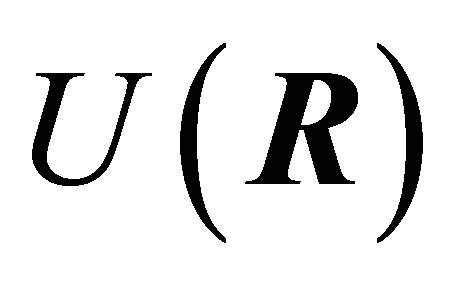 . In the two-level approximation the internal motion of the atom involves only two states:
. In the two-level approximation the internal motion of the atom involves only two states:  of energy
of energy 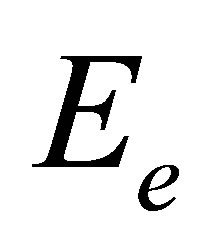 and
and  of energy
of energy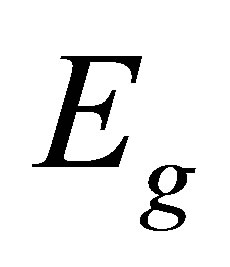 , such that
, such that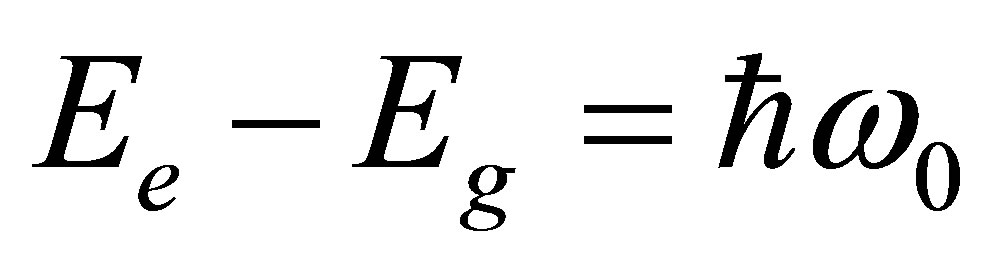 . The operators
. The operators  and
and  are the lowering and raising operators for the internal atomic states such that
are the lowering and raising operators for the internal atomic states such that ; where the operators
; where the operators ,
,  and
and  are the Pulli operators which satisfying the following commutation relations
are the Pulli operators which satisfying the following commutation relations
 (2)
(2)
Finally, 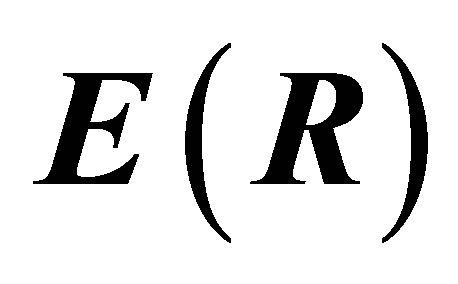 is the electric field operator and
is the electric field operator and  is the electromagnetic field Hamiltonian. The quantized fields inside cylindrical tube are well known [14] and can be written in terms of s-polarized and p-polarized modes satisfying the electromagnetic boundary conditions at the cylindrical walls. We write for
is the electromagnetic field Hamiltonian. The quantized fields inside cylindrical tube are well known [14] and can be written in terms of s-polarized and p-polarized modes satisfying the electromagnetic boundary conditions at the cylindrical walls. We write for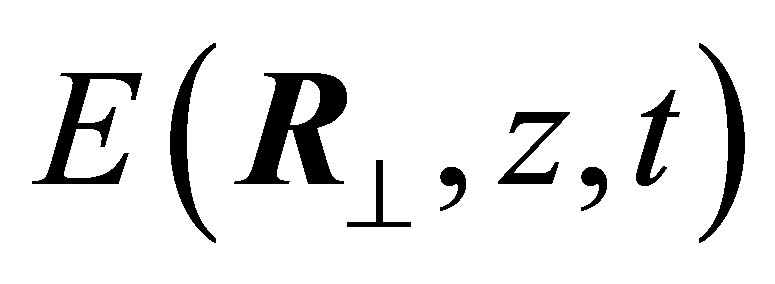 :
:
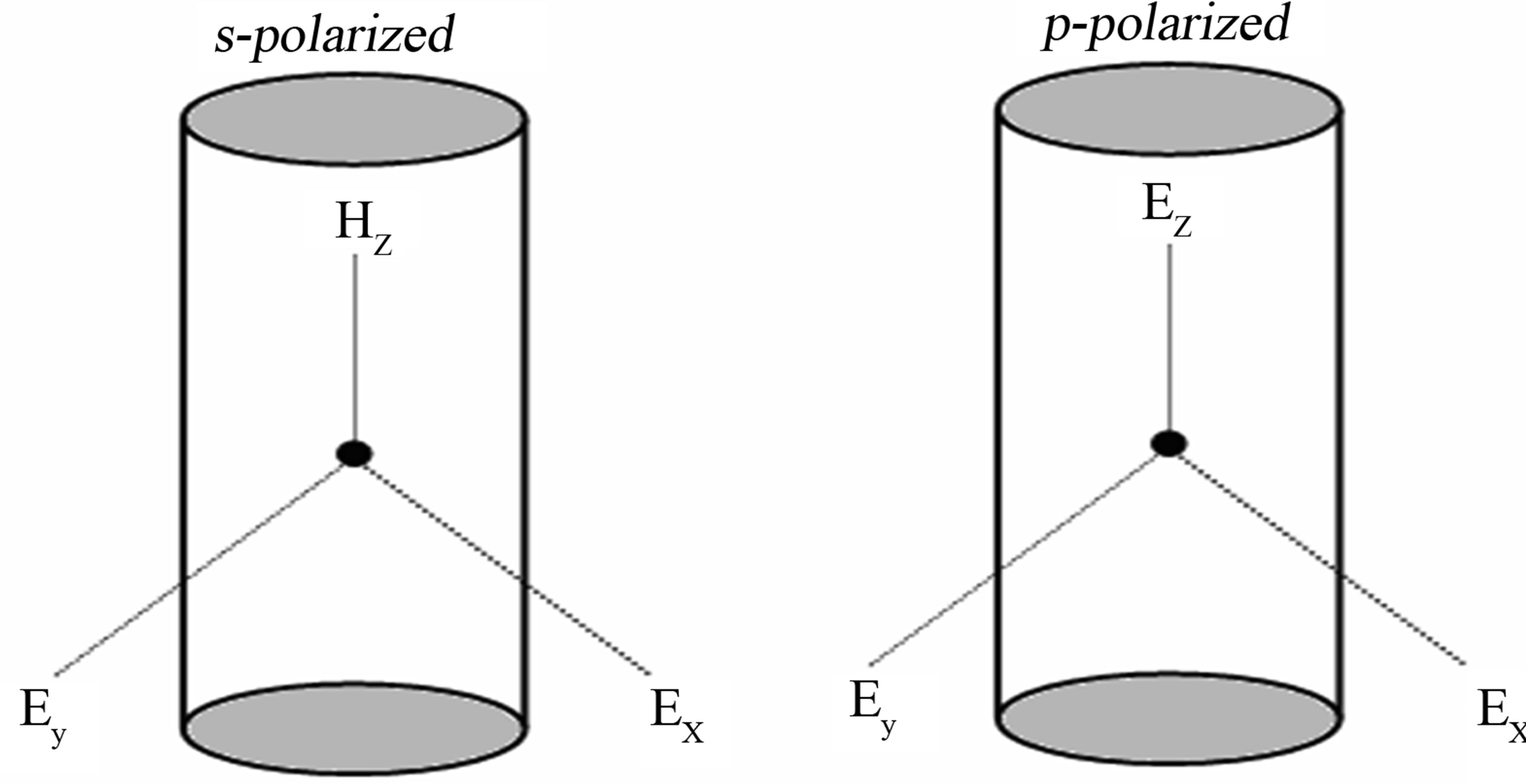
Figure 1. Schematic drawing of the cylindrical tube.
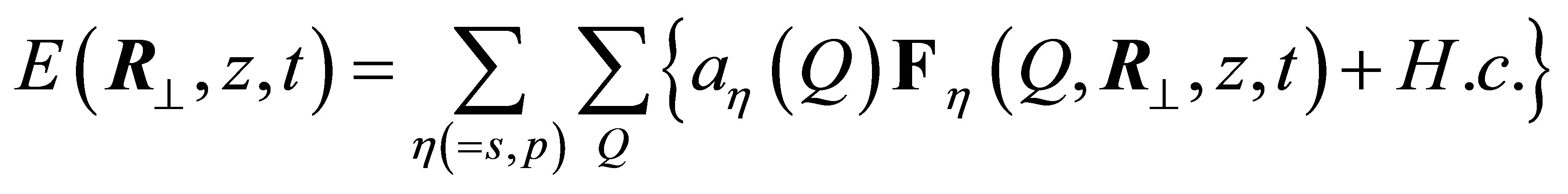 (3)
(3)
where  stands for “Hermitian conjugate”,
stands for “Hermitian conjugate”,  which is a two-dimensional (transverse) position vector and factor
which is a two-dimensional (transverse) position vector and factor  refers to the three mode variables
refers to the three mode variables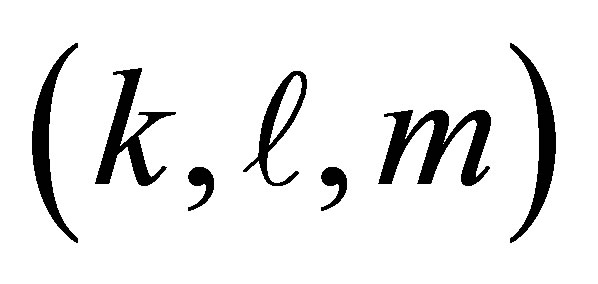 .
.  is the boson operator for the field mode of polarization
is the boson operator for the field mode of polarization , characterized by the integer quantum numbers
, characterized by the integer quantum numbers 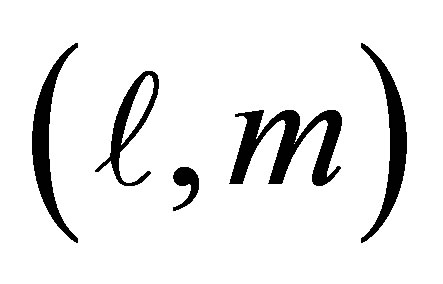 and the longitudinal parallel weave vector
and the longitudinal parallel weave vector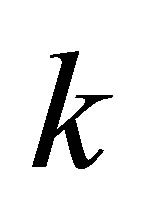 . The relevant commutation relation is:
. The relevant commutation relation is:
 (4)
(4)
where  is given by
is given by
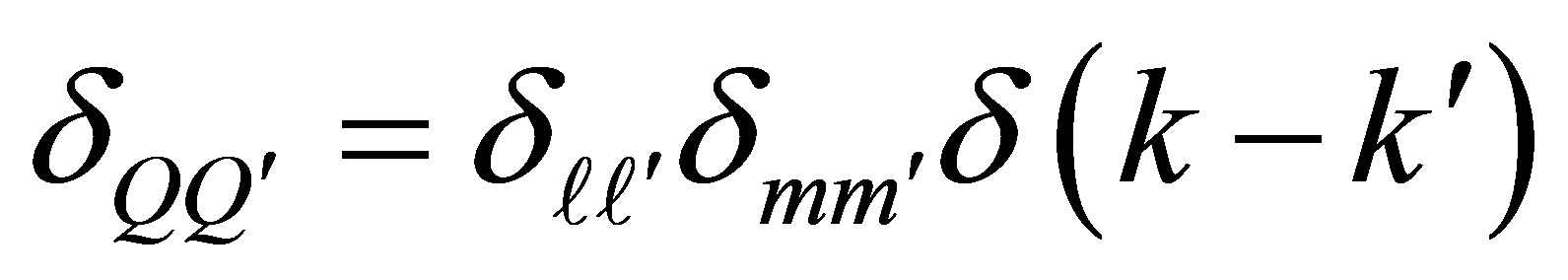 (5)
(5)
Finally,  are the mode functions satisfy electromagnetic boundary conditions at the cylinder walls, these can be written as
are the mode functions satisfy electromagnetic boundary conditions at the cylinder walls, these can be written as
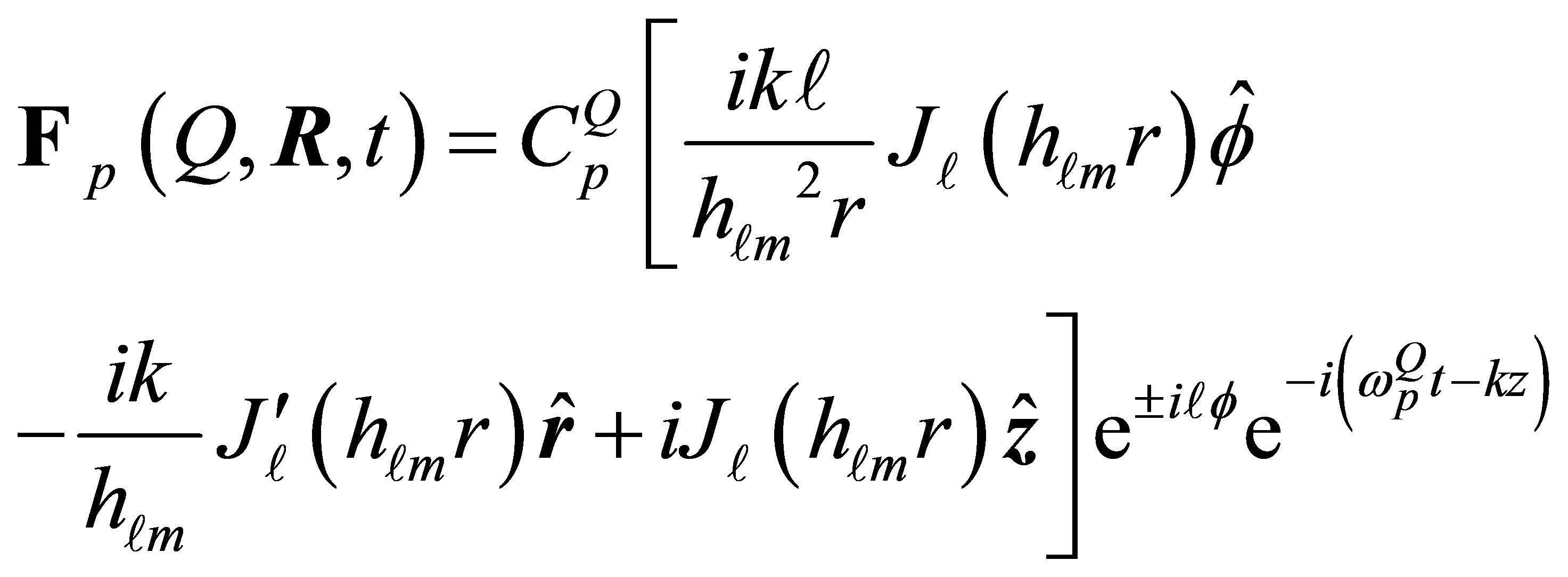 (6)
(6)
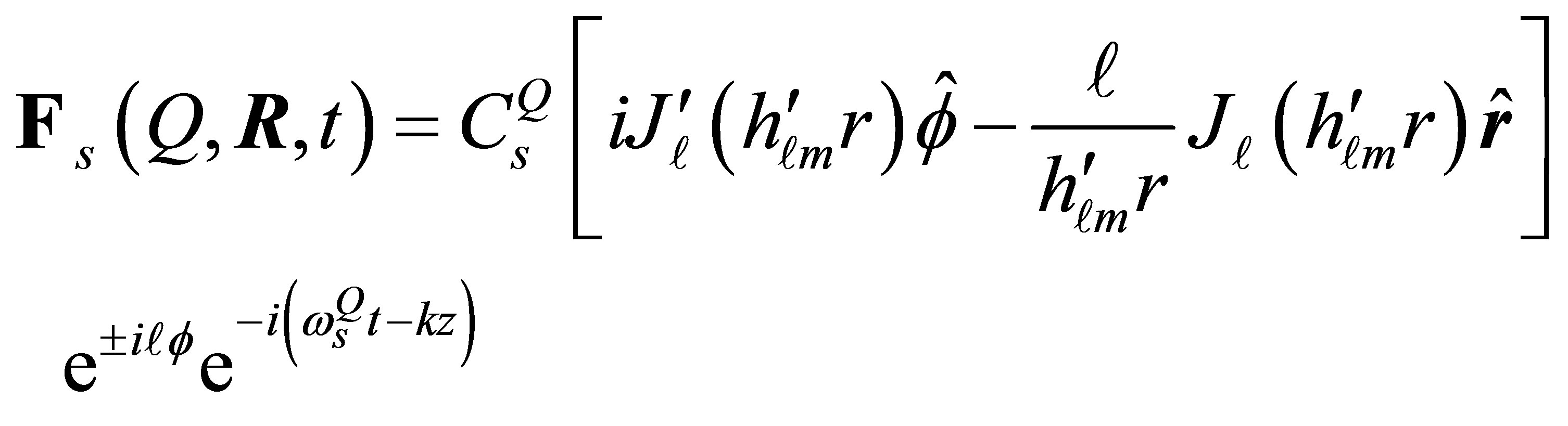 (7)
(7)
where 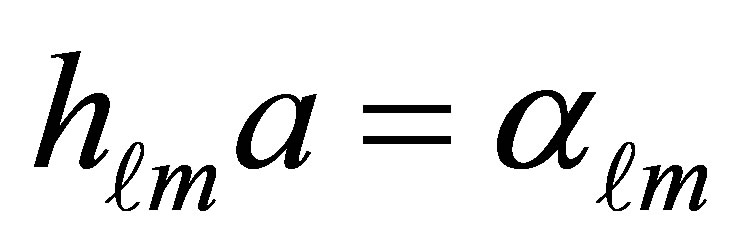 and
and 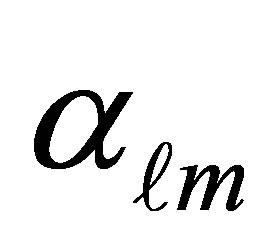 are the roots of the Bessel’s function of the first kind
are the roots of the Bessel’s function of the first kind  while
while  and
and  are the roots of first derivative of Bessel’s function
are the roots of first derivative of Bessel’s function . As well as,
. As well as, 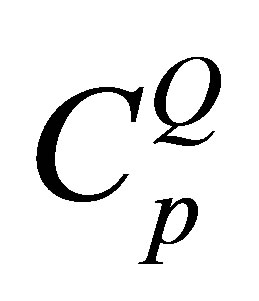 and
and 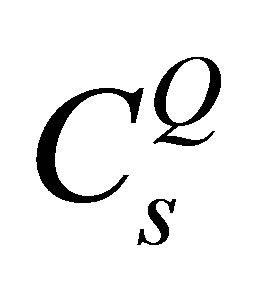 are the normalization factors given respectively by:
are the normalization factors given respectively by:
 (8)
(8)
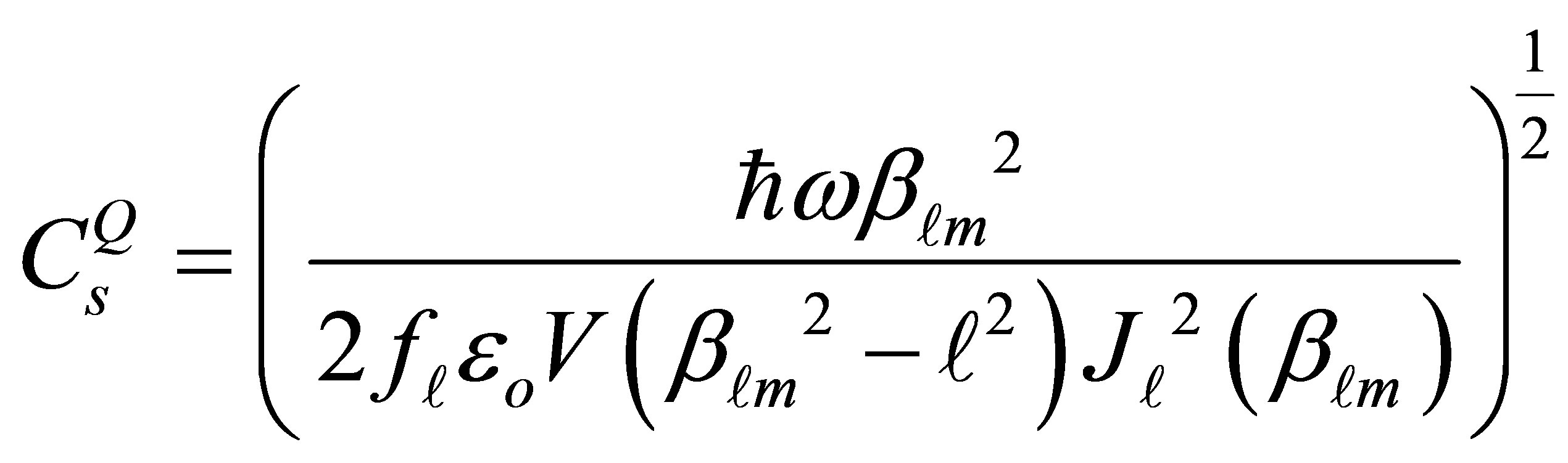 (9)
(9)
where 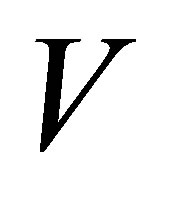 is the quantize volume of the tube,
is the quantize volume of the tube, 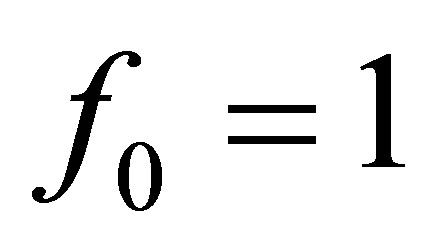 and
and  for
for . Finally, in Equations (7) and (8)
. Finally, in Equations (7) and (8)  and
and , these are the dispersion relation the two polarized modes frequency, they can be written as
, these are the dispersion relation the two polarized modes frequency, they can be written as
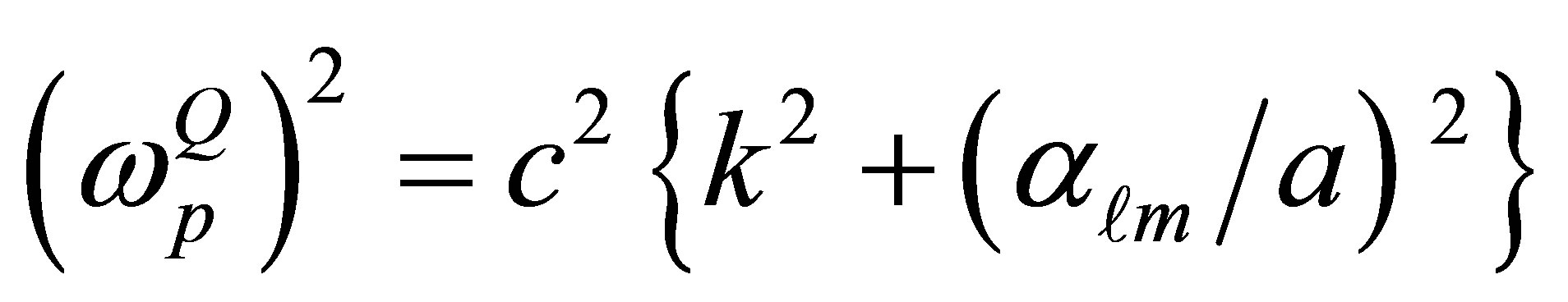 (10)
(10)
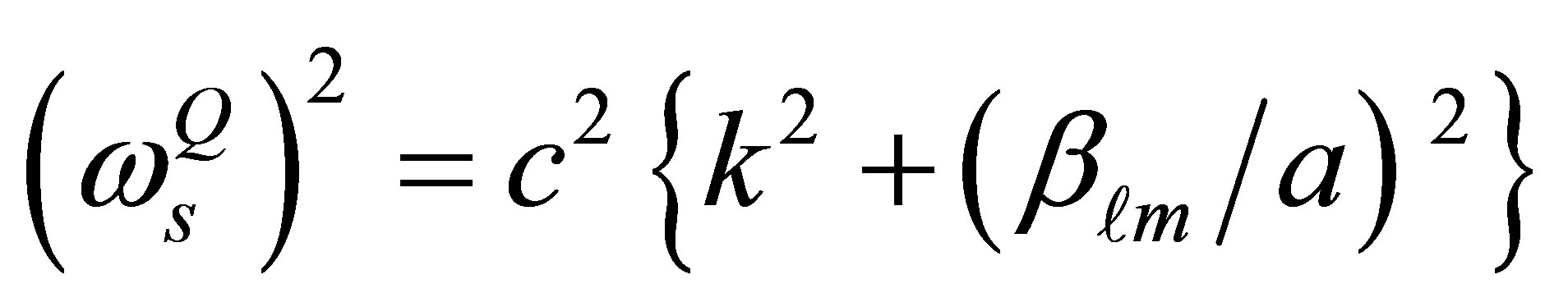 (11)
(11)
The number of propagation modes within the cylindrical tube can be determined by
 (12)
(12)
The optical system we are concerned with, is a cylindrical tube of diameter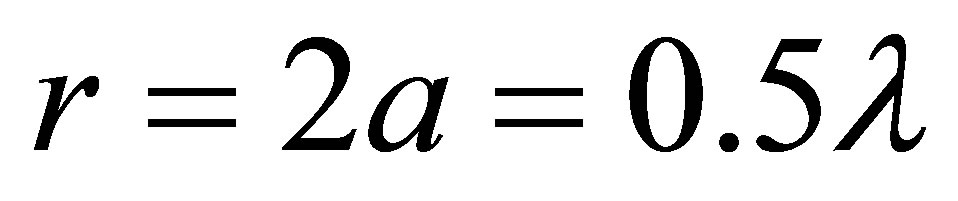 , which is an exact single mode operation system that allows propagation of only one mode. This mode is known as the fundamental mode (the lowest order mode) that is the s-polarized mode with
, which is an exact single mode operation system that allows propagation of only one mode. This mode is known as the fundamental mode (the lowest order mode) that is the s-polarized mode with 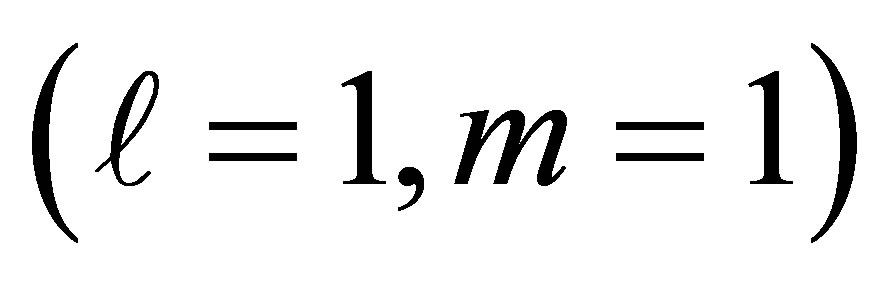 and consequently the Equation (7) will be reduce to
and consequently the Equation (7) will be reduce to
 (13)
(13)
where 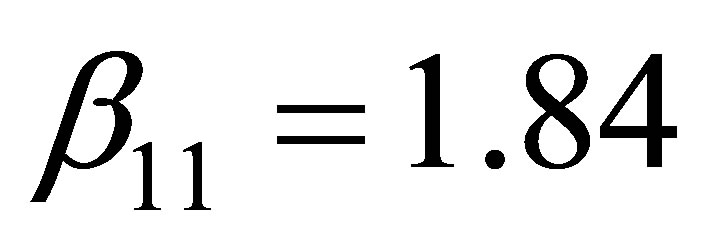 which is the smallest root of all the Bessel function derivatives. On the other hand,
which is the smallest root of all the Bessel function derivatives. On the other hand, 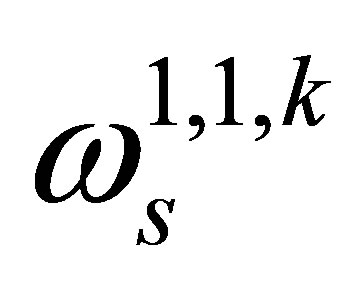 is the mode frequency given by
is the mode frequency given by
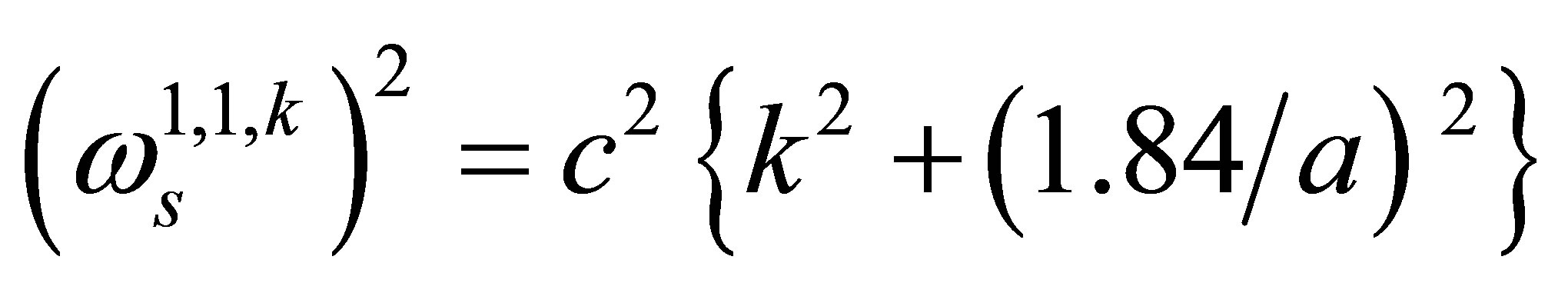 (14)
(14)
Thus cut-off frequency and cut-off wavelength 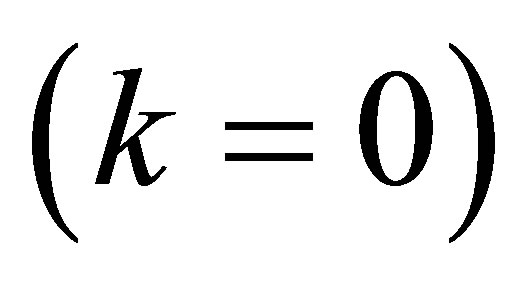 of this lowest mode, are
of this lowest mode, are
 (15)
(15)
3. The Wave Function
In this section we use the effective Hamiltonian for a two-level atom coupled to the quantized field inside cylindrical nanotube in Equation (1) to study the dynamics situation of this optical system. For simplicity we rewrite the effective Hamiltonian as follows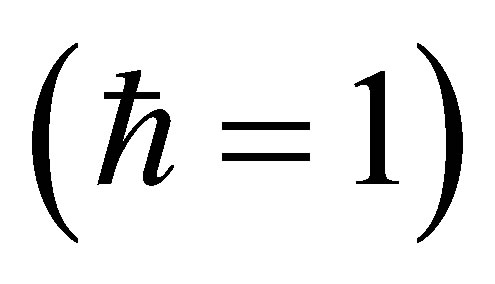 :
:
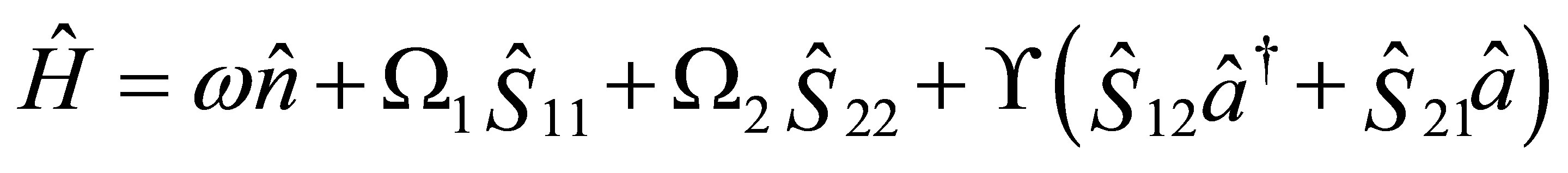 (16)
(16)
where we have taken the Raman-Nath approximation for the atomic Hamiltonian which leads to neglect the kinetic energy term. On the other hand the interaction Hamiltonian part was given in the standard interaction Hamiltonian for a two-level atom interacting with the field in the dipole approximation and the rotating-wave approximation. By introducing the following operators:
 (17)
(17)
 (18)
(18)
with
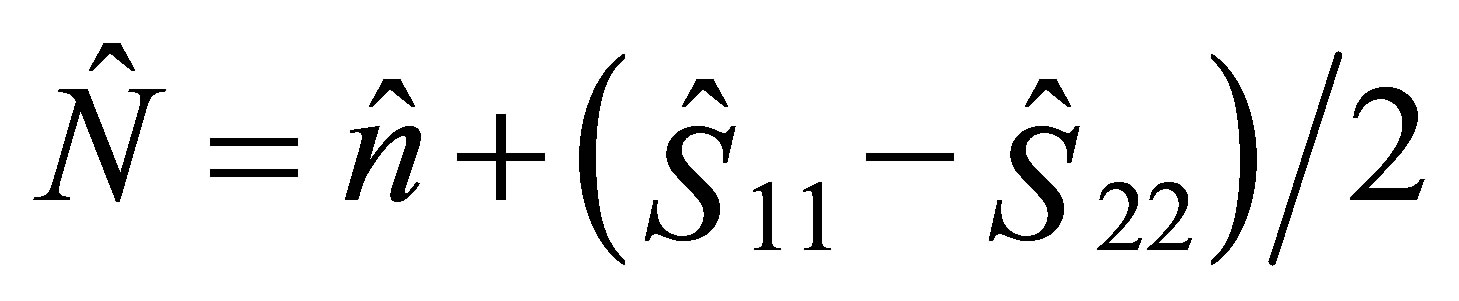 (19)
(19)
where  is the detuning parameter. It is easy to show that
is the detuning parameter. It is easy to show that  and
and  commute with each other and therefore they are constants of motion. In this case, the Hamiltonian (16) can be cast in the following form:
commute with each other and therefore they are constants of motion. In this case, the Hamiltonian (16) can be cast in the following form:
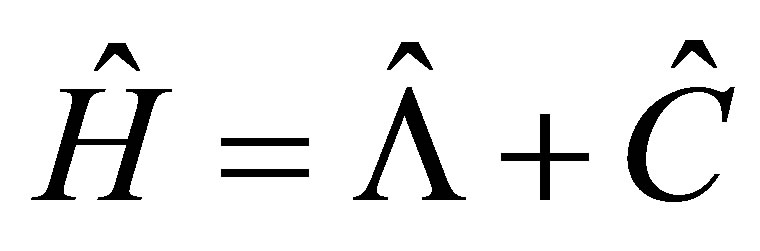 (20)
(20)
At the moment let us consider the atomic coherent state 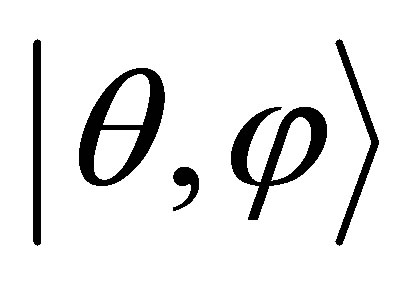 which acquires both excited state
which acquires both excited state 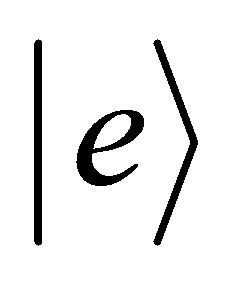 and ground state
and ground state 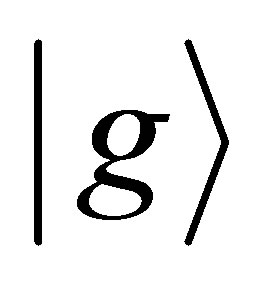 for the two-level atom in the following form:
for the two-level atom in the following form:
 (21)
(21)
In the above equation  is the relative phase of the two atomic levels. To obtain the excited state we have to take
is the relative phase of the two atomic levels. To obtain the excited state we have to take  while to make the wave function describe the particle in the ground state we have to let
while to make the wave function describe the particle in the ground state we have to let . Consequently, if we consider the field to be initially in coherent state
. Consequently, if we consider the field to be initially in coherent state 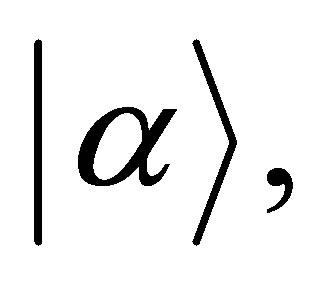 then the initial state of the field takes the form:
then the initial state of the field takes the form:
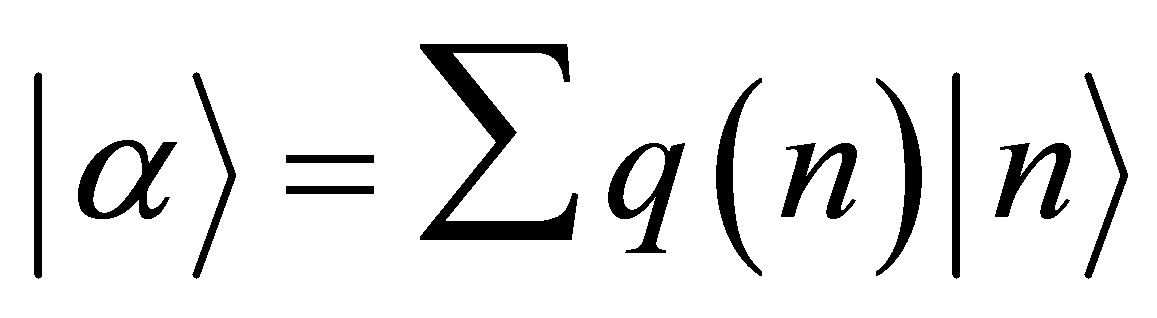 (22)
(22)
where 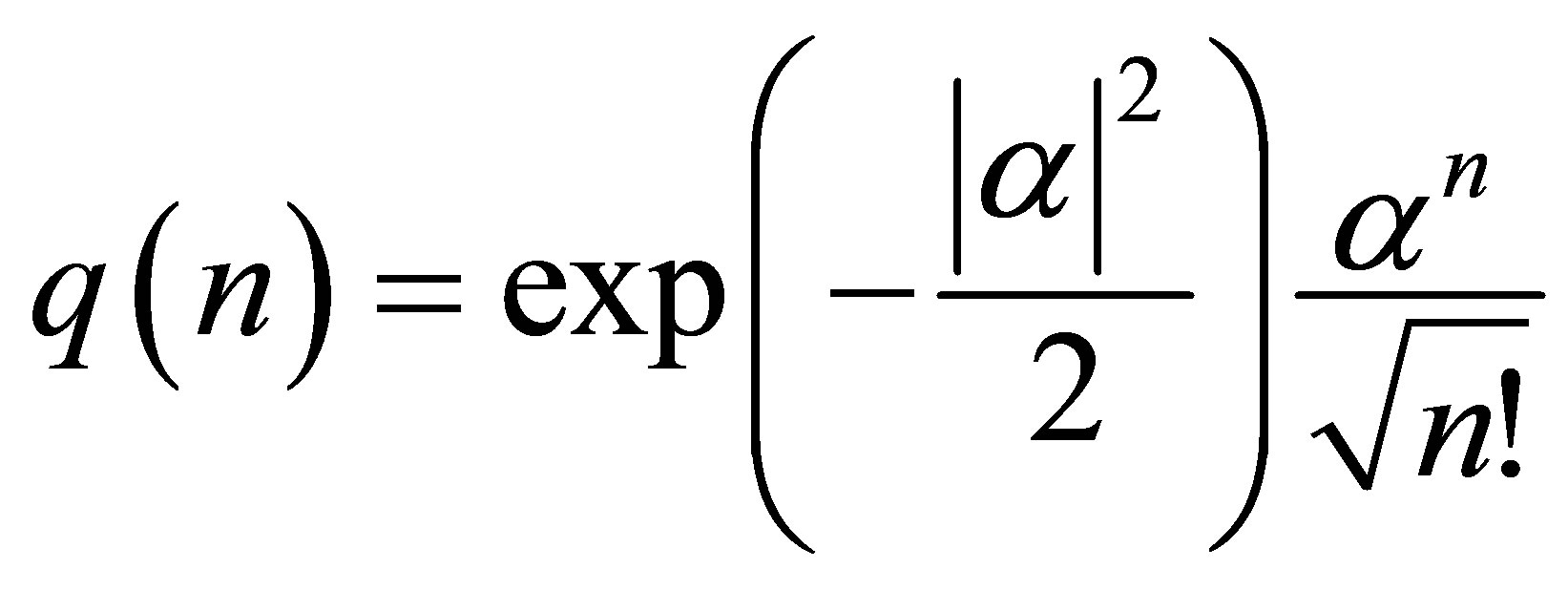 is the amplitude of states
is the amplitude of states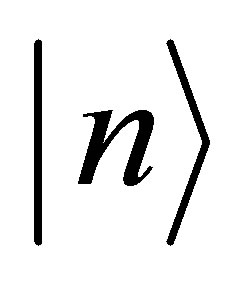 , and
, and 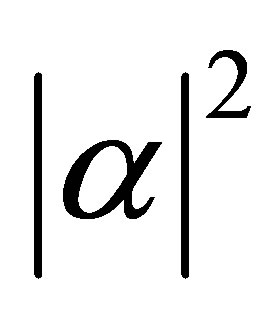 is the initial mean value of the operator
is the initial mean value of the operator  with
with 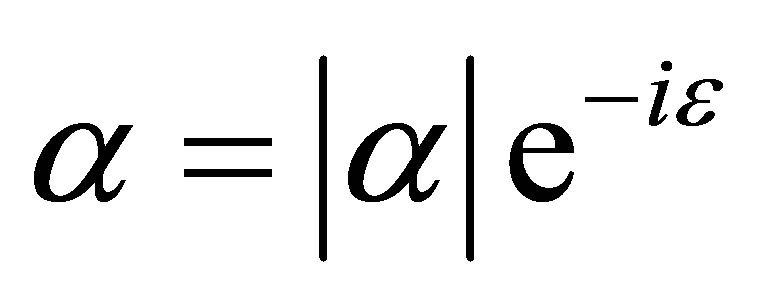 where
where 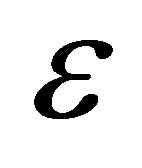 is the phase of coherent state. Assuming that at time
is the phase of coherent state. Assuming that at time  the system is in a pure state, thus the wave function is given by
the system is in a pure state, thus the wave function is given by . Thus, the wave function for the system at any time
. Thus, the wave function for the system at any time 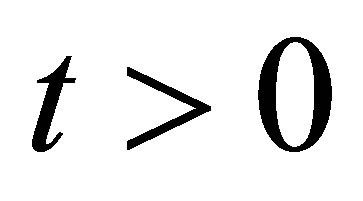 takes the form.
takes the form. , where
, where  is the evolution operator. It is given by
is the evolution operator. It is given by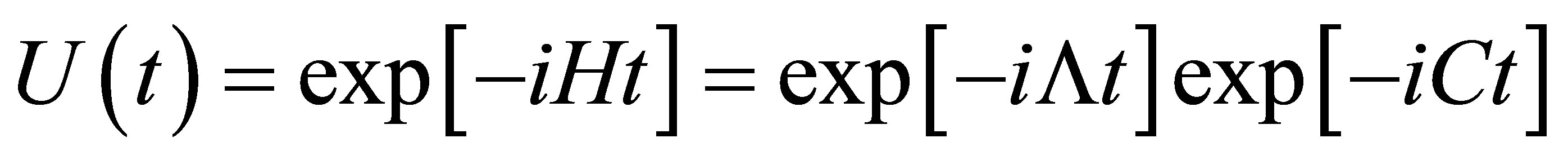 . After straightforward calculations we find that:
. After straightforward calculations we find that:
 (23)
(23)
where
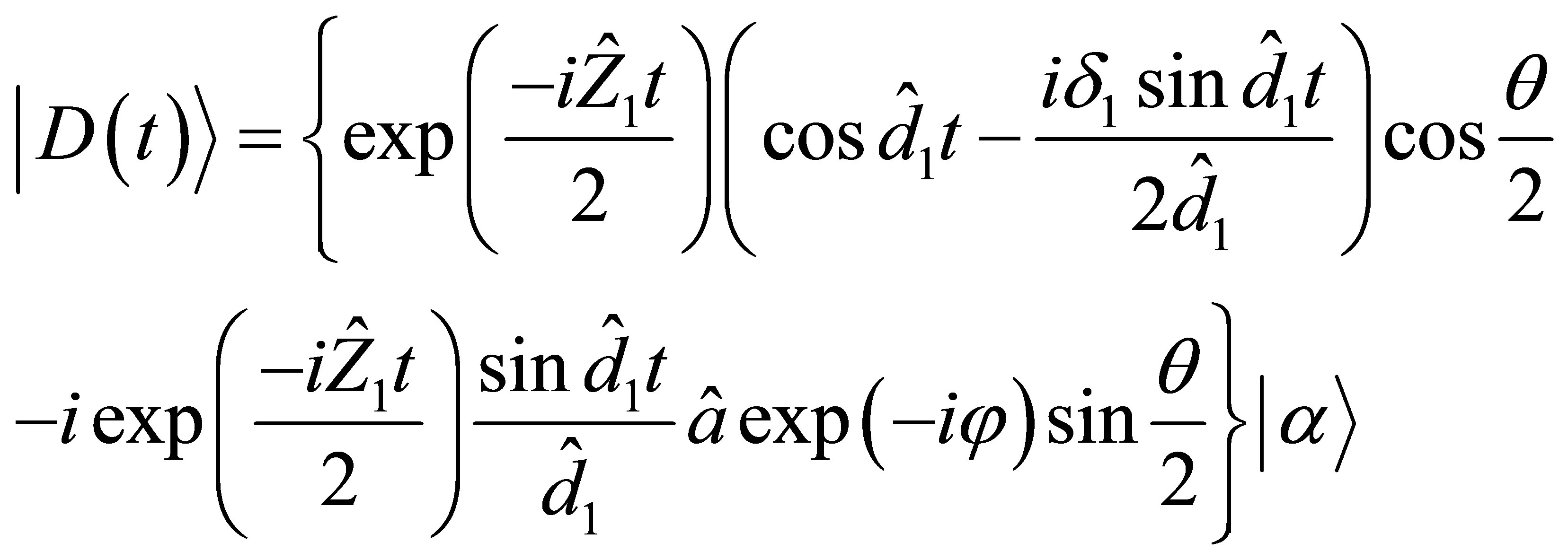 (24)
(24)
and
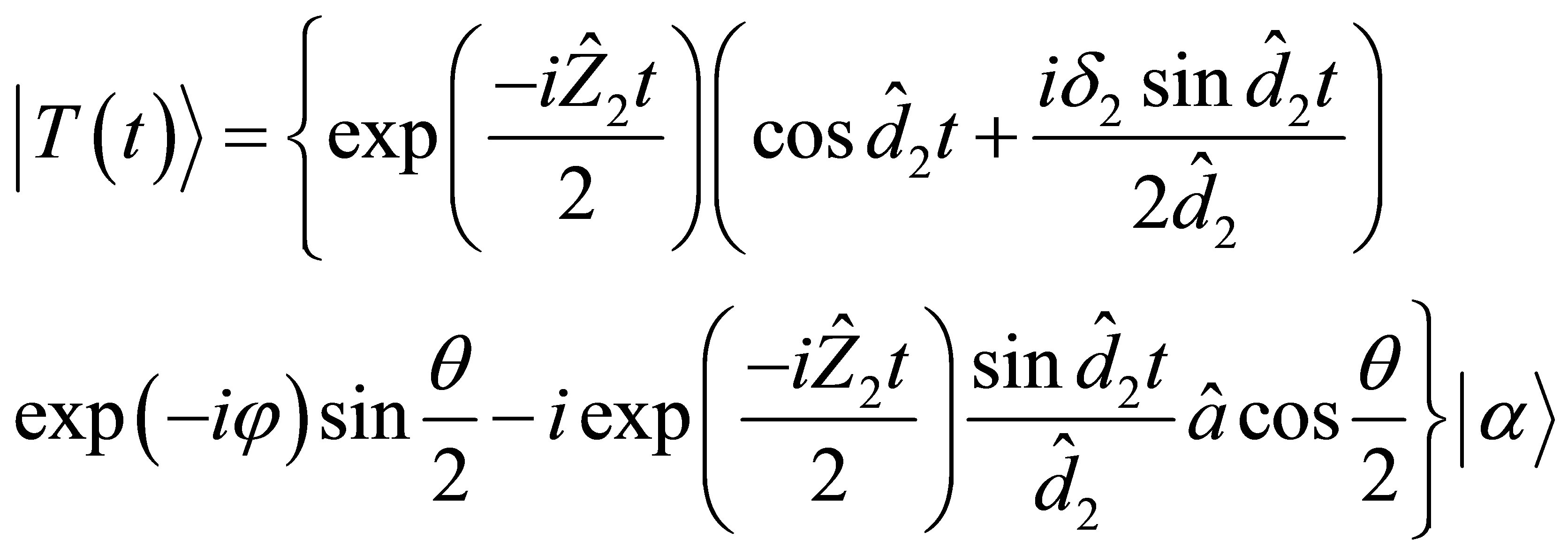 (25)
(25)
with
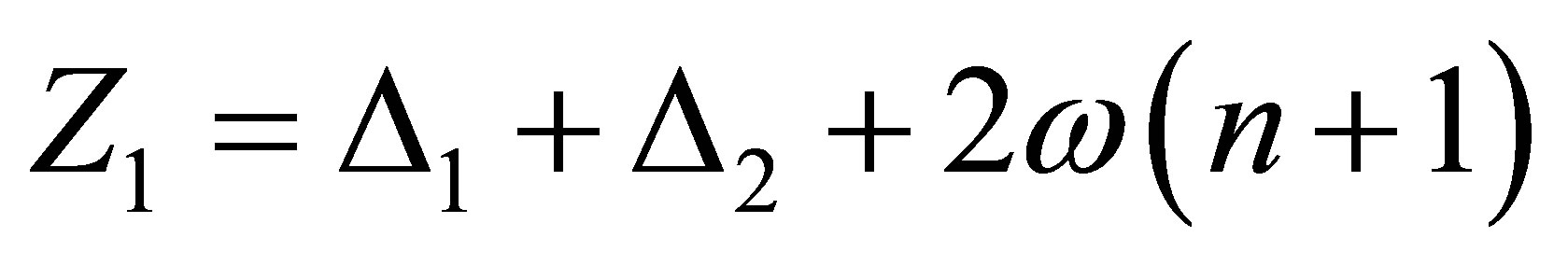 (26)
(26)
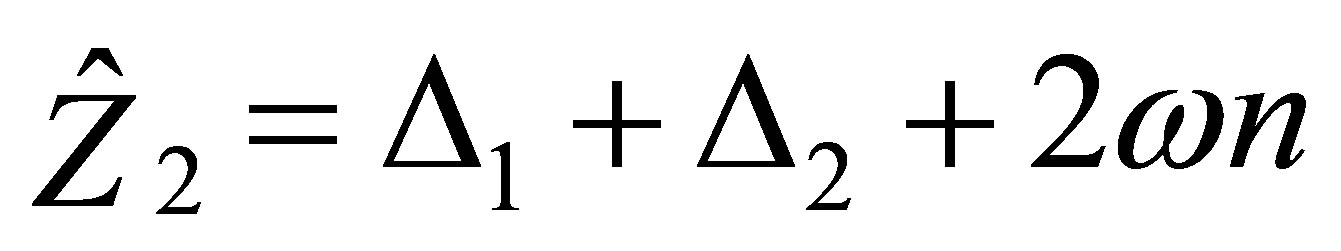 (27)
(27)
where
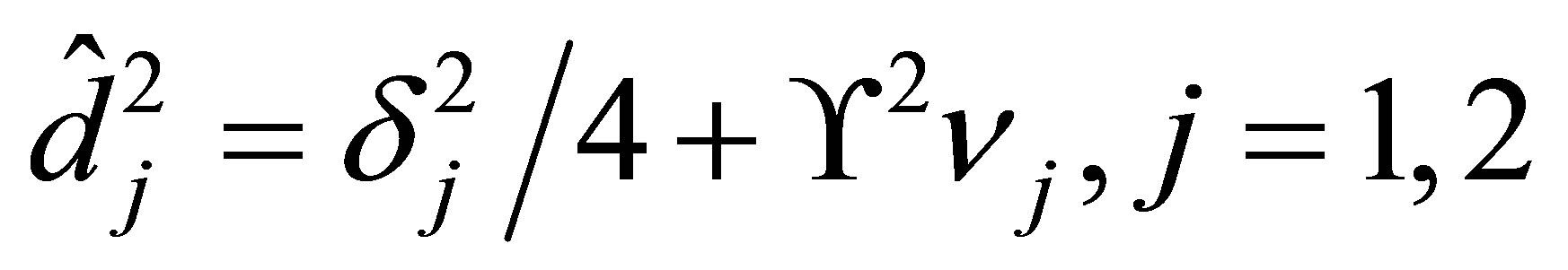 (28)
(28)
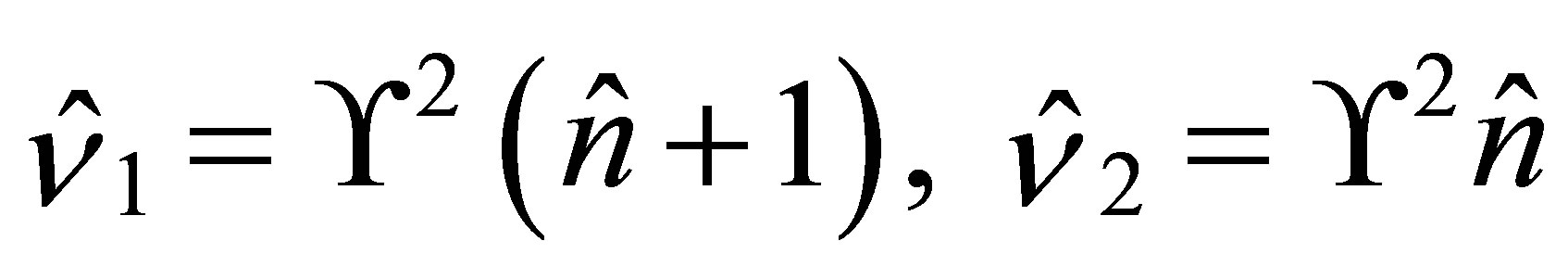 (29)
(29)
The reduced density matrix for the field is given by  , such that:
, such that:
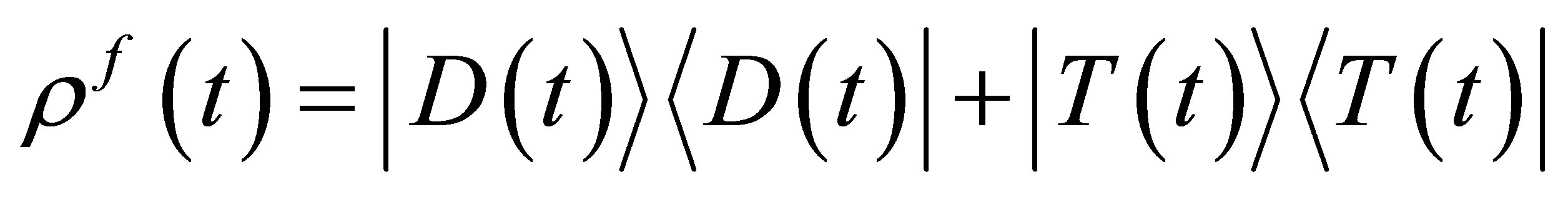 (30)
(30)
where  and
and  are given by Equations (24) and (25) respectively. Once the wave function is computed, we can calculate any expectation value related to the atom or the field which is done in the next sections.
are given by Equations (24) and (25) respectively. Once the wave function is computed, we can calculate any expectation value related to the atom or the field which is done in the next sections.
4. Atomic Inversion
The atomic inversion is defined as the difference between the probabilities of fining the atom in the excited state and in the ground state. Not only we use the atomic inversion to observe the atom in excited or ground state but also observe that the atom reach to maximal state. The maximal state defined as the probabilities of fining the atom in excited state and ground state are equal. If we assume the atom starts in its excited state, we can show that the atomic inversion 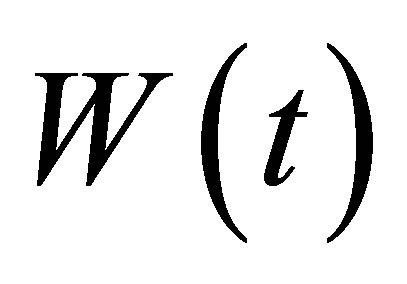 take the following form:
take the following form:
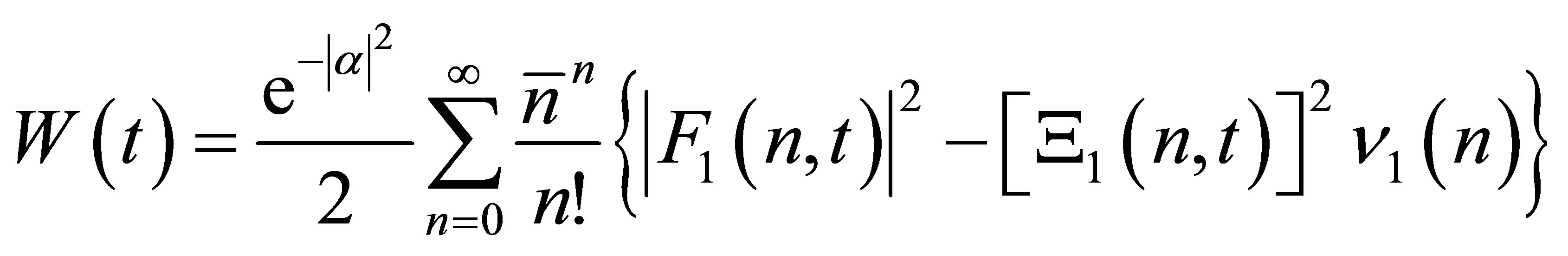 (31)
(31)
where
 (32)
(32)
 (33)
(33)
We note that the expectation value for  can be obtained directly from the constant of motion
can be obtained directly from the constant of motion 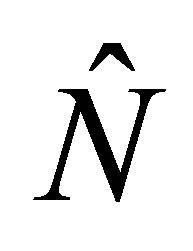 of Equation (19). Then we find collapse and revivals comparable to the coherent state (JCM). The revival time can be estimated as in refs. [6,7] to be the time revival in four photons. It is estimated as
of Equation (19). Then we find collapse and revivals comparable to the coherent state (JCM). The revival time can be estimated as in refs. [6,7] to be the time revival in four photons. It is estimated as 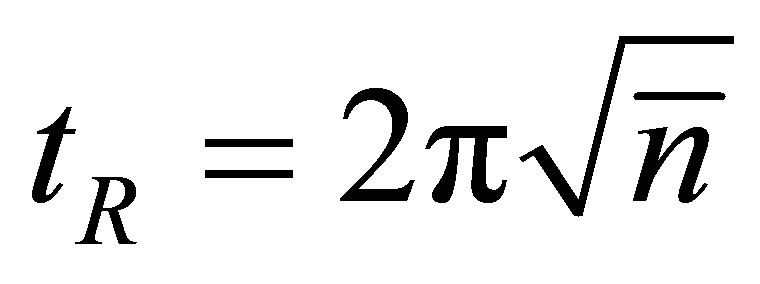 for the coherent input. In our numerical investigations we plot the atomic inversion against time
for the coherent input. In our numerical investigations we plot the atomic inversion against time  taking into consideration the atom initially in the excited state and the field is prepared in a coherent state with
taking into consideration the atom initially in the excited state and the field is prepared in a coherent state with .
.
In Figure 2, we consider the sodium atom case with wavelength transition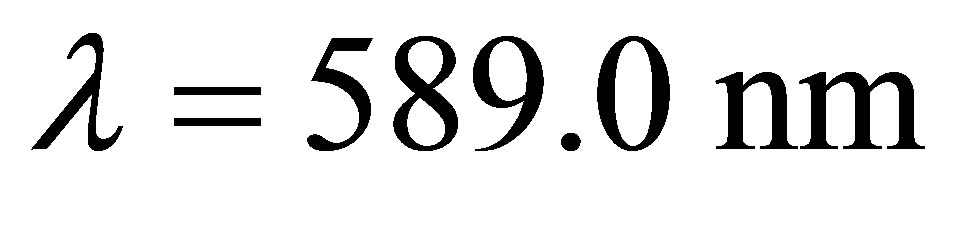 , which means that the maximum value of the cylinder radius is
, which means that the maximum value of the cylinder radius is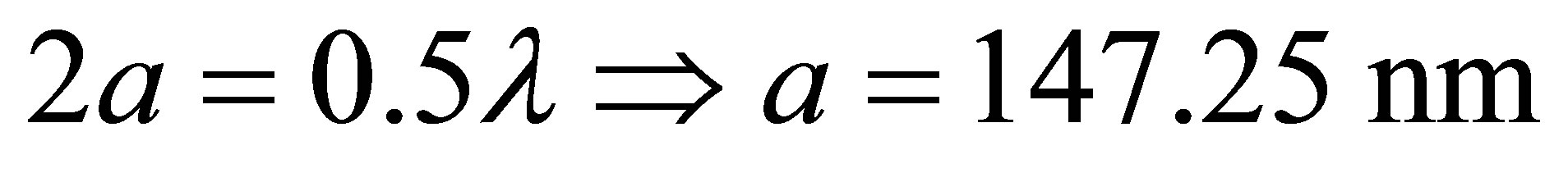 . We see that the flip from the upper to lower state occurring partially and collapse and revivals phenomenon of the atomic inversion is apparent. The revival at
. We see that the flip from the upper to lower state occurring partially and collapse and revivals phenomenon of the atomic inversion is apparent. The revival at  which is in compliance with the estimated value. We note that the inversion oscillates around the value
which is in compliance with the estimated value. We note that the inversion oscillates around the value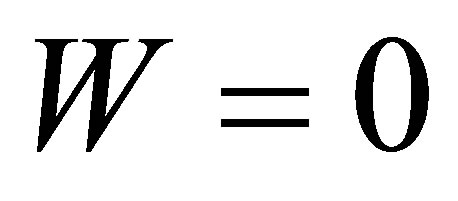 .
.
The maximal state occurring at the collapses time and periodically as shown in Figure 2. While in Figure 3, we take another example, the rubidium atom with wavelength transition 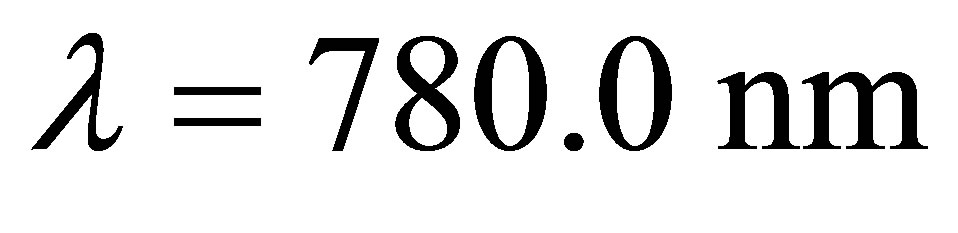 (which means that the cylinder radius will be
(which means that the cylinder radius will be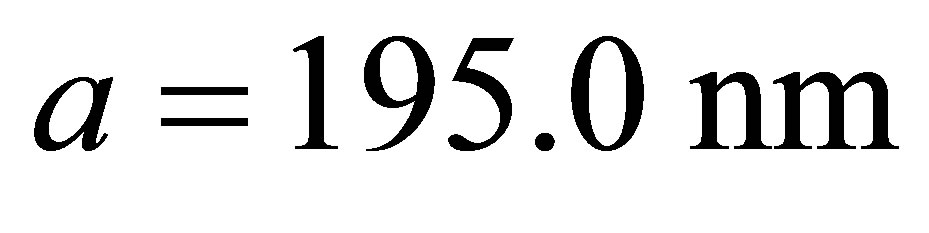 ). It’s clear that after
). It’s clear that after

Figure 2. The evolution of the atomic inversion with the intensity of the initial coherent field equal to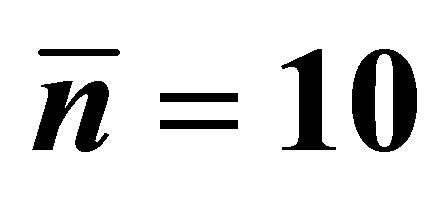 ,
, 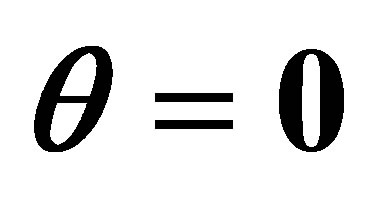 and
and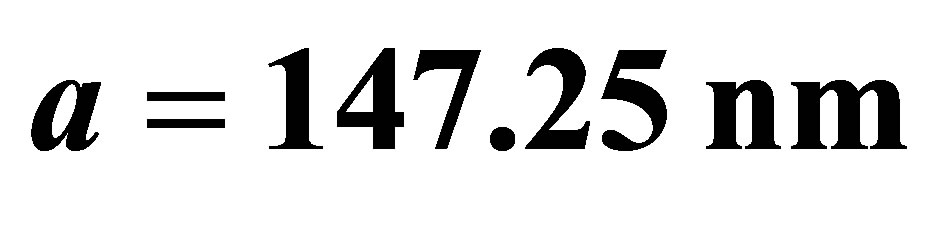 .
.
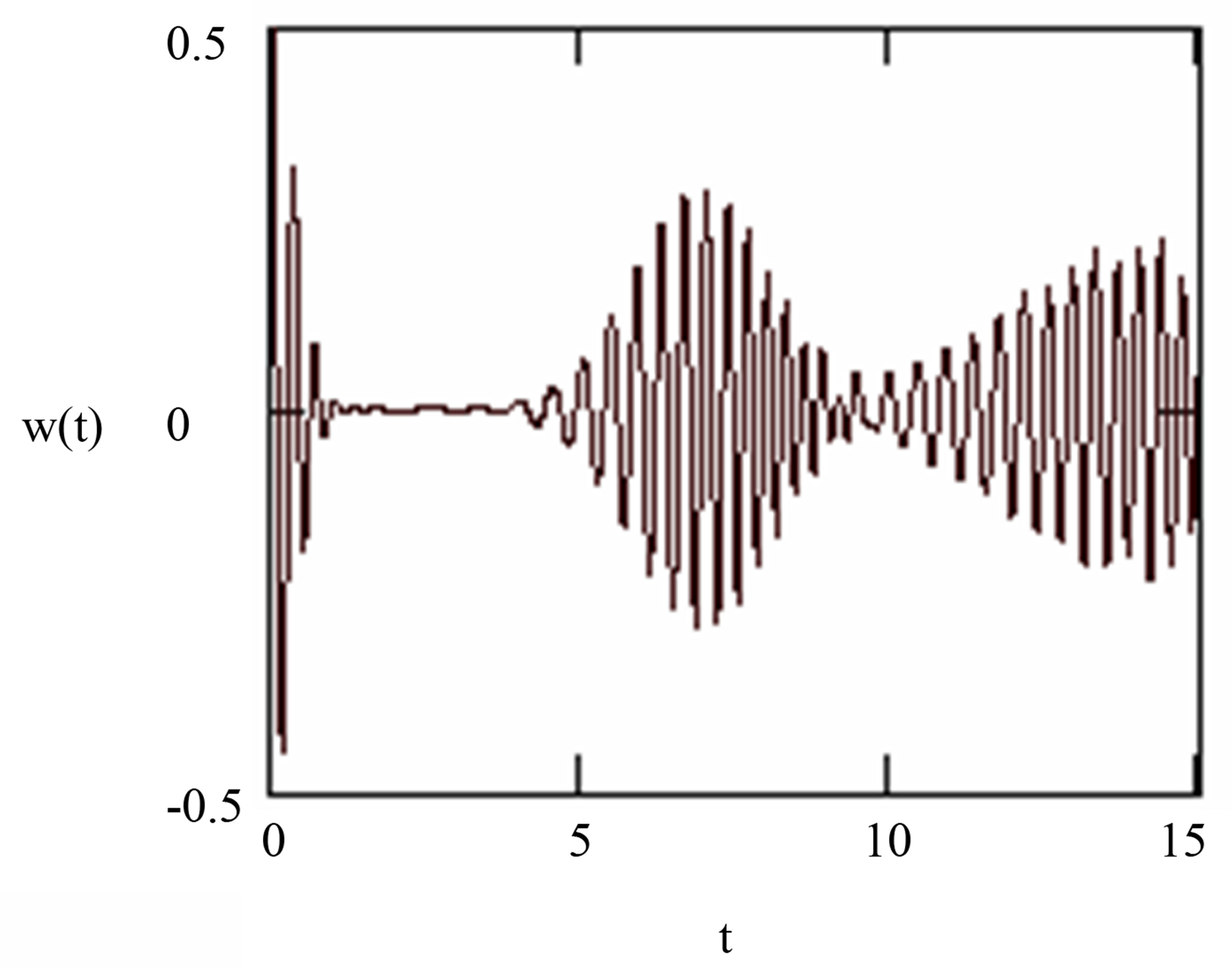
Figure 3. The evolution of the atomic inversion with the intensity of the initial coherent field equal to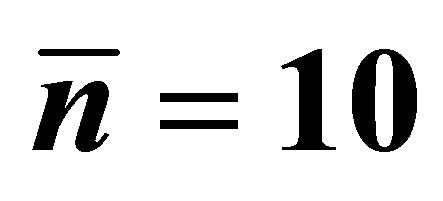 ,
,  and
and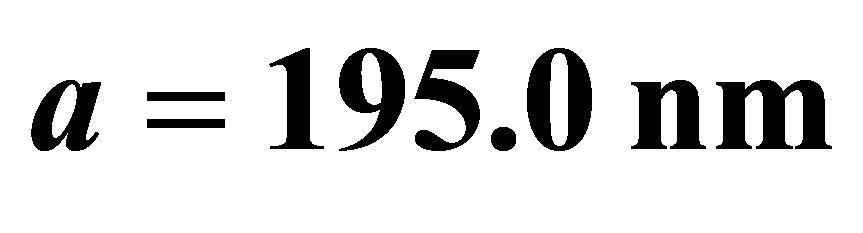 .
.
increasing of the parameter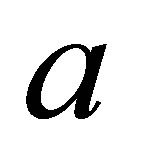 , the time of maximal state occurring increases. It is noted that the parameter
, the time of maximal state occurring increases. It is noted that the parameter 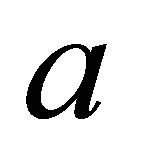 increases the collapses and revivals to occur at long intervals. In general the behavior of the function is changed markedly, however it shows an increase the time of the collapses (the atom reach to maximal state).
increases the collapses and revivals to occur at long intervals. In general the behavior of the function is changed markedly, however it shows an increase the time of the collapses (the atom reach to maximal state).
5. Quantum Field Entropy
In this section, we use the field entropy as a measure of the degree of entanglement between the field and the atom of the system under consideration. The quantum dynamics described by the Hamiltonian (16) leads to an entanglement between the quantum field and the atom, which will be quantified by the field entropy. A suitable diagnostic tool is the entropy [18,19]
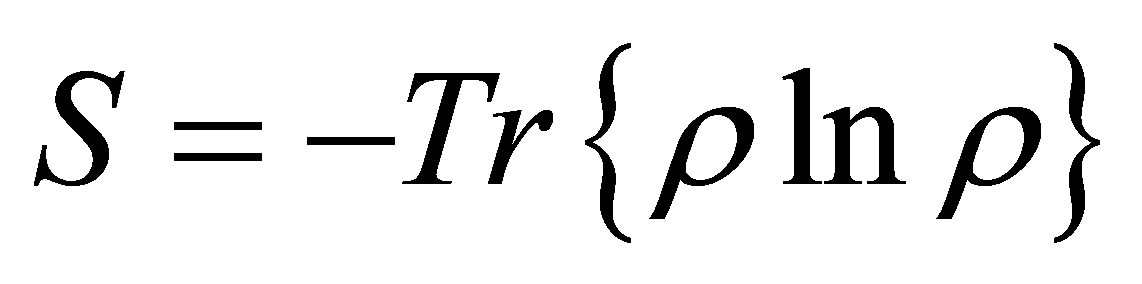 (34)
(34)
where  is the density operator for a given quantum system and we have set Boltzmann’s constant
is the density operator for a given quantum system and we have set Boltzmann’s constant . If the atom is in a pure state, then in a suitable bases the density matrix is diagonal and has a single unit element. For this case
. If the atom is in a pure state, then in a suitable bases the density matrix is diagonal and has a single unit element. For this case , while if
, while if 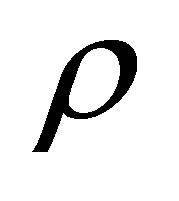 describes a mixed state, then
describes a mixed state, then . Since the initial state is a pure state, then
. Since the initial state is a pure state, then , either
, either 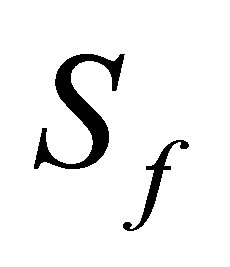 the field entropy or
the field entropy or 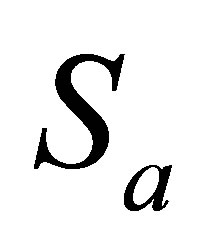 the atomic entropy is used to measure the amount of entanglement between the two subsystems. When
the atomic entropy is used to measure the amount of entanglement between the two subsystems. When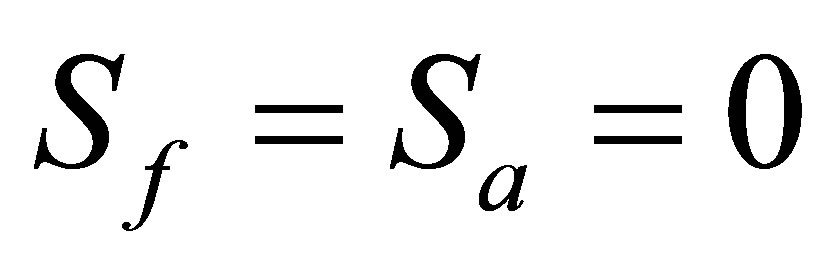 , the system is disentangled or separable and both the field and atomic subsystems are in pure states. The entropies of the particle and the field, are defined through the corresponding reduced density operators by:
, the system is disentangled or separable and both the field and atomic subsystems are in pure states. The entropies of the particle and the field, are defined through the corresponding reduced density operators by:
 (35)
(35)
provided we treat both separately. Since the trace is invariant under a similarity transformation, then we can go to a basis in which the density matrix of the field is diagonal and then express the field entropy 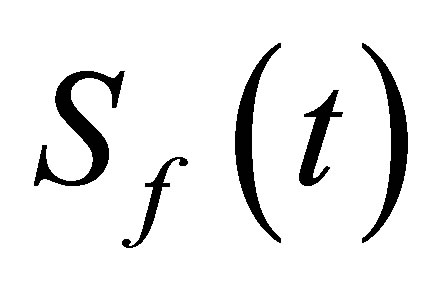 in terms of the eigenvalue
in terms of the eigenvalue 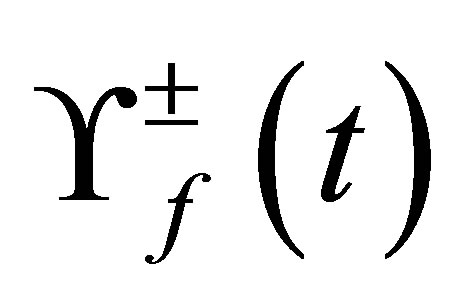 for the reduced field density operator. A general method to calculate the various field eigenstates in a simple way has been developed [20]. By applying this method, we can obtain the eigenvalues for the reduced density operator thus:
for the reduced field density operator. A general method to calculate the various field eigenstates in a simple way has been developed [20]. By applying this method, we can obtain the eigenvalues for the reduced density operator thus:
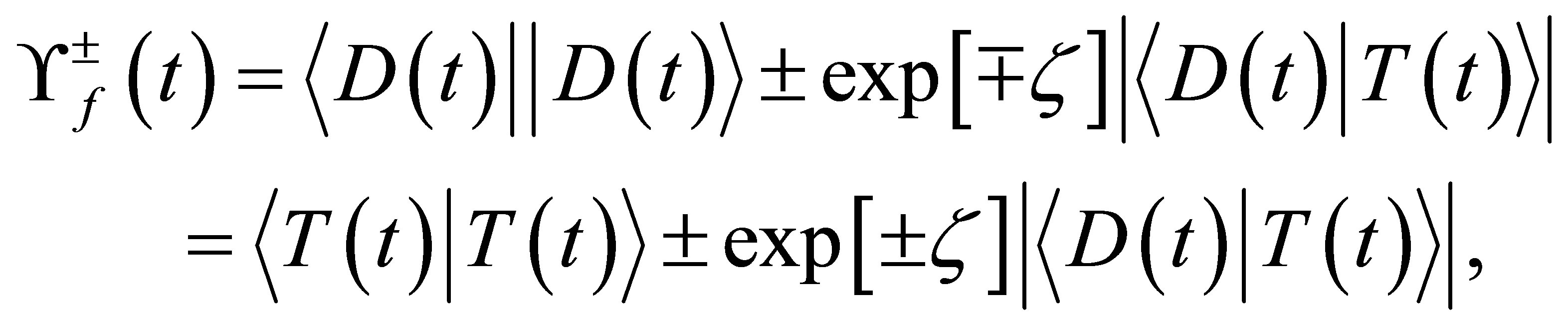 (36)
(36)
where
 (37)
(37)
The field entropy 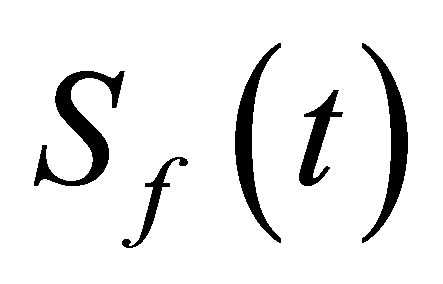 may be expressed in terms of the eigenvalues
may be expressed in terms of the eigenvalues 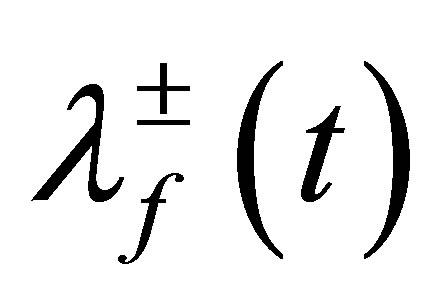 for the reduced field density operator as:
for the reduced field density operator as:
 (38)
(38)
Now we turn our attention to examine numerically the dynamics of the field entropy we use the same initial parameters of the earlier figures. By using the same initial parameters of the earlier figures. We observe that when  (for the sodium atom) the entropy is dynamically reduced to the minimum values at
(for the sodium atom) the entropy is dynamically reduced to the minimum values at  and the tube field can not reach to the pure state. It is note that the entanglement increased at the atom papered in maximal state. In Figures 2 and 3 the maximal states are occurring at the collapses and the maximum degree of entanglement occurring at same time see Figure 4. For the second case when
and the tube field can not reach to the pure state. It is note that the entanglement increased at the atom papered in maximal state. In Figures 2 and 3 the maximal states are occurring at the collapses and the maximum degree of entanglement occurring at same time see Figure 4. For the second case when  (for the rubidium atom), which is observed in Figure 5, we see that the entropy is stable (do not oscillated) at long time compared with the previous case. This meaning that the time of maximal state increase by the parameter
(for the rubidium atom), which is observed in Figure 5, we see that the entropy is stable (do not oscillated) at long time compared with the previous case. This meaning that the time of maximal state increase by the parameter  increases.
increases.
It is important to note that the atoms confined trans-

Figure 4. The time evolution of the field entropy for the same initial condition and parameter of Figure 2.

Figure 5. The time evolution of the field entropy for the same initial condition and parameter of Figure 3.
versely within the tube are prone to a diffusive increase of the atomic momentum in longitudinal direction (wavevector 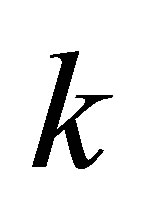 has one continuous degrees of freedom along z-direction) which will minimize the entanglement process. Definitely, this is better than the case of two-plates system that have two continuous degrees of freedom [8,9]. Subsequently, to avoid completely this problem, we can take a quantum size of an empty closed cylindrical resonator [21].
has one continuous degrees of freedom along z-direction) which will minimize the entanglement process. Definitely, this is better than the case of two-plates system that have two continuous degrees of freedom [8,9]. Subsequently, to avoid completely this problem, we can take a quantum size of an empty closed cylindrical resonator [21].
Over and above, by assuming inner walls to be a perfect conducting and so exclude all electromagnetic fields from their interior. In this situation, the standard electromagnetic boundary conditions apply such that the tangential components of the electric field vector and the magnetic field vector must vanish at every point on the inner walls. Consequently, the energy injected during a very short time can remain stored inside tube for a very long time in comparison with the period, which means a very high quality factor Q. Furthermore to this intrinsic property, the closed resonator, in general, is a very significant for the theory of an optical confinement of individual atoms by the mechanical forces associated with single photons. This kind of confinement represents elementary quantum systems that are well isolated from the environment. Recently, many experimental studies are concerned with the open geometries as suitable of interaction environment for atom optics [15]. These geometries have clear advantages when it comes to loading the confine and, possible, further manipulating the atoms (e.g. cooling, trapping, mode selecting), but they suffer from the problem that it is relativity easy for atoms to escape. While close geometries confine atom in all directions and a particular mode can be excited from a tiny hole at an appropriate location in the outer surfaces. This hole may connect directly with the laser source or by a tube which a commonly method for coupling mode to a close geometries. This is the main reason why two-dimensional tubes system cannot, in general, be employed as an efficient entanglement environments.
6. Conclusions
In this paper, we have examined in detail the properties of the entanglement between an atom and the electromagnetic field inside cylindrical nanotube. The tube modes are first quantized, allowing the effective Hamiltonian to be evaluated for an electric dipole located at an arbitrary point. We have shown that in the limit of small tube radius, especially when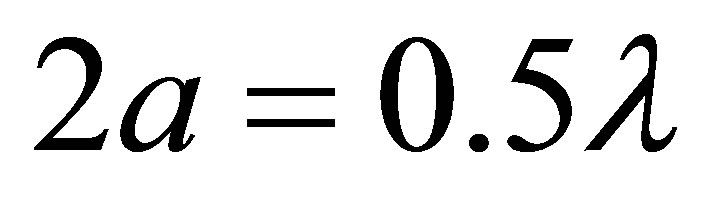 , only the fundamental mode s-polarized mode with
, only the fundamental mode s-polarized mode with 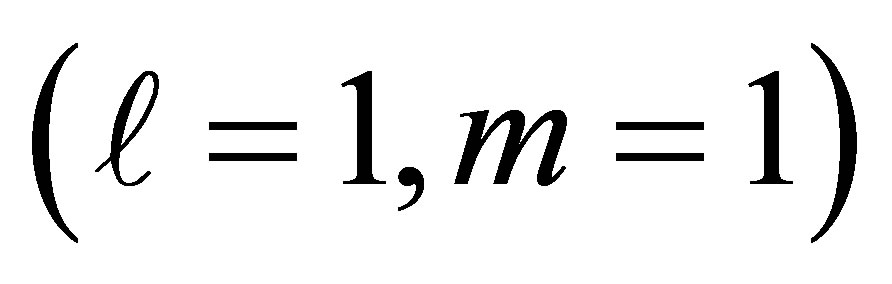 is allowed to propagate within the tube. Therefore, the system became an exact single mode operation and thus the atom only interacts with a single mode.
is allowed to propagate within the tube. Therefore, the system became an exact single mode operation and thus the atom only interacts with a single mode.
We have explored the temporal evolution of the atomic inversion and the von Neumann entropy. These processes have been depending on the radius of the tube. For the atomic inversion, we have shown that the atom stay in maximal entangled state when the radius of the tube is large. The degree of this entanglement has been measured by the von Neumann entropy.
In addition, this work shows that the general feature explored here is the entanglement between atom and the position independent mode with  inside nanotube system is different on the entanglement between atom and the position dependent higher modes inside the same system. In fact, the above considerations of the entanglement process of the position independent mode have now paved the way for considering the entanglement process of the position dependent mode that could be given more efficient entanglement process. An obvious line of extension of this work should consider cylindrical tube with walls made of dielectrics characterized by dispersive dielectric functions which could also exhibit loss. A theory focusing on such features can, additionally, accommodate the first type of tube namely, the evanescent mode tubes which can now have the new feature of submicron dimensions. Although the decay emission of atoms in dialectic tubes has been fully investigated [17], the entanglement process in this structure has not been reported before. Work along these lines is now in progress and the results will be reported in due course.
inside nanotube system is different on the entanglement between atom and the position dependent higher modes inside the same system. In fact, the above considerations of the entanglement process of the position independent mode have now paved the way for considering the entanglement process of the position dependent mode that could be given more efficient entanglement process. An obvious line of extension of this work should consider cylindrical tube with walls made of dielectrics characterized by dispersive dielectric functions which could also exhibit loss. A theory focusing on such features can, additionally, accommodate the first type of tube namely, the evanescent mode tubes which can now have the new feature of submicron dimensions. Although the decay emission of atoms in dialectic tubes has been fully investigated [17], the entanglement process in this structure has not been reported before. Work along these lines is now in progress and the results will be reported in due course.
7. Acknowledgements
The author wish to express their gratitude to Dr. E. Khalil for useful discussion and for prepare of these works.
REFERENCES
- M. Nielsen and I. Chuang, “Quantum Computation and Information,” Cambridge University Press, Cambridge, 2000.
- P. G. Kwiat, K. Mattle, H. Weinfurter, A. Zeilinger, A. V. Sergienko and Y. Shih, Physical Review Letters, Vol. 75, 1995, pp. 4337-4342. http://dx.doi.org/10.1103/PhysRevLett.75.4337
- B. Kraus and J. I. Cirac, Physical Review Letters, Vol. 92, 2004, pp. 013602-013608. http://dx.doi.org/10.1103/PhysRevLett.92.013602
- S. Sorensen and K. Molmer, Physical Review Letters, Vol. 90, 2003, pp. 127903-127908. http://dx.doi.org/10.1103/PhysRevLett.90.127903
- C. Marr, A. Beige and G. Rempe, Physical Review A, Vol. 68, 2003, pp. 033817- 033822. http://dx.doi.org/10.1103/PhysRevA.68.033817
- K. Molmer, Optics Communications, Vol. 179, 2000, pp. 429-435.
- J. I. Cirac, P. Zoller, H. J. Kimble and H. Mabuchi, Physical Review Letters, Vol. 78, 1997, pp. 3221-3226. http://dx.doi.org/10.1103/PhysRevLett.78.3221
- S. A. Al-Awfi and E. M. Khalil, International Review of Physics, Vol. 3, 2008, pp. 147-153.
- E. M. Khalil, Journal of Modern Physics, Vol. 2, 2011, pp. 724-729. http://dx.doi.org/10.4236/jmp.2011.27085
- S. Marksteiner, C. M. Savage, P. Zoller and S. L. Rolston, Physical Review A, Vol. 50, 1994, pp. 2680-2690. http://dx.doi.org/10.1103/PhysRevA.50.2680
- M. A. Ol’Shanii, Y. B. Ovchinnkov and V. S. Letokhov, Optics Communication, Vol. 98, 1993, pp. 77-79. http://dx.doi.org/10.1016/0030-4018(93)90761-S
- M. J. Renn, E. A. Donley, E. A. Cornell, C. E. Wieman and D. Z. Anderson, Physical Review A, Vol. 53, 1996, pp. R648-R651. http://dx.doi.org/10.1103/PhysRevA.53.R648
- S. Al-Awfi and M. Babiker, Physical Review A, Vol. 61, 2000, Article ID: 033401. http://dx.doi.org/10.1103/PhysRevA.61.033401
- S. Al-Awfi and M. Babiker, Physical Review A, Vol. 58, 1998, pp. 4768-4778. http://dx.doi.org/10.1103/PhysRevA.58.4768
- J. P. Dowling and J. Gea-Banacloche, Advances in Atomic, Molecular, and Optical Physics, Vol. 37, 1996, pp. 1-94. http://dx.doi.org/10.1016/S1049-250X(08)60098-1
- H. Nha and W. Jhe, Physical Review A, Vol. 56, 1997, pp. 2213-2219. http://dx.doi.org/10.1103/PhysRevA.56.2213
- S. Al-Awfi, Indian Journal of Physics, Vol. 8, 2013, pp. 819-825. http://dx.doi.org/10.1007/s12648-013-0289-1
- M. M. A. Ahmed, E. M. Khalil and A.-S. F. Obada, Optics Communications, Vol. 254, 2005, pp. 76-84. http://dx.doi.org/10.1016/j.optcom.2005.05.016
- A.-S. F. Obada, M. M. A. Ahmed and E. M. Khalil, Journal of Modern Optics, Vol. 53, 2006, pp. 1149-1155. http://dx.doi.org/10.1080/09500340600551440
- E. Hinds, Advances in Atomic, Molecular, and Optical Physics, Vol. 2, 1993, pp. 1-56.
- S. Al-Awfi, S. Bougouffa and M. Bawa’aneh, International Journal of Nanomanufacturing, Vol. 4, 2009, pp. 92-98. http://dx.doi.org/10.1504/IJNM.2009.028115

