Journal of Modern Physics
Vol.4 No.9(2013), Article ID:36940,5 pages DOI:10.4236/jmp.2013.49161
A Phenomenological Model for the Electromagnetic Origin of Mass in Particles, and Its Quantitative Application to the Electron, the Muon, the Proton, and the Neutron
Departamento de Física, Universidade Federal de Santa Catarina, Florianópolis, Brazil
Email: osvaldo.neto@ufsc.br
Copyright © 2013 Osvaldo F. Schilling. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received July 2, 2013; revised August 6, 2013; accepted August 26, 2013
Keywords: Mass; Particle Physics; Particles Models; Particle Radius; Flux Quantization
ABSTRACT
A simple phenomenological model is developed, which indicates the existence of a direct link between the concept of rest mass of a particle and magnetodynamic energies associated to the formation of the particle. The model is based upon the principles of quantization and conservation of flux, well known for their application in superconductivity. The charge of particles is considered as forming vortices of superconducting currents, which we postulate are created by electromagnetic fluctuations from vacuum (or related processes). A new quantization rule gathers the size, the magnetic moment, and the rest mass of the particle and associates these quantities to the integer number of flux quanta that should be stored in the vortices corresponding to each particle. The model is applied to the electron, the muon, the proton, and the neutron. Quantitative consistency with available experimental data for these subatomic particles is obtained.
1. Introduction
The field of Particle Physics is deservedly considered one of the most demanding within all the different branches of Theoretical Science. Group Theory and Quantum Field Theory in all its mathematical complexity are used to deal with processes of particles scattering, of creation and destruction of particles, among many other problems inherent to this area of research. What we intend to show in this paper is that some of the most important properties of subatomic particles like the electron, the proton, and the neutron, can definitely be gathered and analyzed without Field Theoretical methods, and still produce new information about a dramatically important issue, i.e., the origin of mass itself. The inextricable association between mass and a magnetic moment for those particles results from this analysis, which reveals also a quantitative link between mass and magnetodynamic energy.
Of course such analysis can by no means rely upon classical physics methods and models. Particles exist in a femtometer-scale environment dominated by quantum mechanics and relativity theory, and thus quantum mechanics is the tool to be used. Therefore, although the analysis to be proposed is essentially phenomenological, since measured properties and data for the particles are used throughout, a fundamental piece of quantum mechanical result is inserted into the model at a key spot, turning it quantitatively consistent with the expected physical behavior of the systems under consideration.
The exposition of this model thus starts in Section 2 with the discussion of the concept of mass for classical oscillating systems in general, and then specializes in the case of the superconductor electromechanical oscillator (SEO) [1-3]. The SEO will be taken as the basis for the analysis of the subatomic particles. The relation between mass and magnetodynamic energies for the SEO is described, and shown to depend on the magnetic flux associated with the supercurrents flowing round the oscillating loop of the SEO. In Section 3, the results of the previous section are extrapolated to apply to the subatomic particles, and arguments are presented in support to this approach. This corresponds to starting with a large-scale model of a “particle” and then shrinking it to the femtometer scale, while keeping the validity of the Physics of the system for this further application. Important experimentally measurable parameters for the electron, the muon, the proton, and the neutron are shown to be gathered together in a single formula, a new quantization rule dictated by the requirements of flux quantization.
2. The Concept of Mass for “Ideal” Mechanical and Electromechanical Oscillating Systems
In a recent publication [1] the concept of mass as a quantity describable in terms of stored energy has been discussed in detail, for the case of idealized linear springload oscillating systems. If the spring-load system is initially fully at rest with no stored energy, the imposition of a constant force F at t = 0 leads to the following relation between the mass of the load m and the stored energy E:
 (1)
(1)
where vm is the maximum speed of the oscillating load [1]. Equation (1) is the result of the following important property: mass can be defined in terms of energy when the object oscillates in full dynamic equilibrium with the force fields around it. For instance, in the case of the ideal linear spring-load system with F the weight of the load, one would have in action the gravitational field and the spring elasticity field. The source for E is the work done upon the system by F along the range of oscillation, which is kept stored in view of the restitution effect of the spring [1]. The definition of mass in Equation (1) includes this restitution effect. Energy in this resonating state would continuously shift between the gravitational potential, kinetic and elastic kinds of energy, and mass would then be described in terms of the total energy stored in this resonance. The discussion in [1] then concentrates on a system which follows a similar behavior, the superconductor electromechanical oscillator-SEO (see Figure 1). Such system has been analyzed in detail in
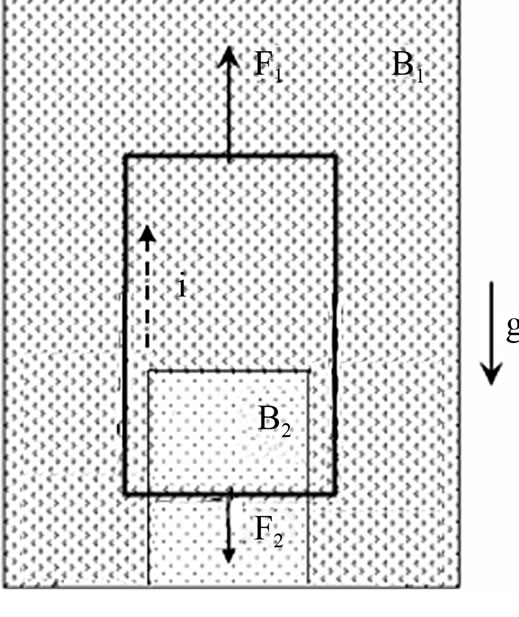
Figure 1. The SEO [1-3]. A type-II superconductor loop levitates under the effect of two magnetic fields B1 and B2 greater than its lower critical field (B1 > B2 in the figure and the fields point into the page). F1 and F2 are the opposing vertical Lorentz forces that the fields impose upon the current i induced in the loop when it is initially released and moves under the effect of gravity g. The loop reaches dynamic equilibrium with the force fields around it.
recent years [1-4] in view of its extreme stability, and applications have been devised. It has been shown in [2,4] that this system when hanging upright under certain experimental conditions should display a Q on the order of 107 or much greater depending on vacuum conditions, very low temperatures and absence of inductive coupling with nearby metallic parts. The movement of the rectangular loop is perfectly analogous to that for a linear spring-load system. In particular, Equation (1) applies to the motion. It can readily be shown from the simultaneous solution of Newton’s and Faraday’s Laws applied to the motion of the loop that E in Equation (1) can be written purely in magnetodynamic terms [1]:
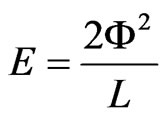 (2)
(2)
In this equation Φ = Li is the flux due to the average superconducting current i that flows around the loop, and L is the selfinductance of the loop. The loop levitates while performing micrometer-range one-dimensional oscillations under the effect of its own weight and the restoring magnetic forces. Once again, the object is in full equilibrium with the surrounding fields, and thus its mass can be expressed in terms of the energy of this resonance. Furthermore, the energy is of magnetodynamic character. The work done upon the loop by the external force (the loop weight in this case) generates motion against the external magnetic fields, and a supercurrent is induced in the loop associated with the transformation of the work into magnetodynamic energy, which is stored due to the flux conservation property of superconductors.
The foregoing analysis is the basis for the model that follows. Note that a redefinition of mass in terms of energy has been introduced. The redefinition is valid provided the system reaches dynamic equilibrium with the force fields around it. We judge that such redefinition might be extended from large-scale objects like the SEO loop, down to the femtometer-scale of particles. The key for such extension would be the respect to quantum mechanical conditions which would dictate the Physics at the femtometer-scale dimensions. This clearly reminds us of the Correspondence Principle proposed in the 1920s by the Copenhagen School of Bohr, Born, Heisenberg, and others, according to which classical physics results should be obtained from quantum mechanics in the limit of large quantum numbers. As we argue below, such extension from large to small quantum numbers is also found in this analysis.
3. Extension to Particle Physics
One starts by wondering if a similar interpretation for mass might be applied to some other physical system. For instance, if currents are induced spontaneously due to electromagnetic fluctuations, forming stable loops or vortices in the femtometer-size scale, in equilibrium with the surrounding fields (in which conditions such vortices might become stable is not clear, but a criterion will be proposed below). In the superconductor oscillator case, the external force in the presence of the external magnetic fields triggers the motion of the loop and an induced supercurrent is generated, which traps energy and makes the loop reach dynamic equilibrium with the fields. In a microscopic scale such effects would take place due to fluctuations in electric and magnetic forces creating and then acting upon the stabilized vortices of charge. In the case the currents are resistanceless a magnetic energy would be trapped and the vortices would oscillate under some restoring force due to the fields around. The discussion in Section 2 suggests that the quantity mass might again be defined for such vortices in a way analogous to the large-scale superconducting loop. What follows is the result of an extrapolation of the analysis of the Physics of the SEO, and its comparison with the known properties of subatomic particles, like the proton, the neutron, and also the electron and the muon. These particles would be considered as localized vortices with trapped energy, in equilibrium with the surrounding fields.
3.1. A Phenomenological Quantization Rule and Its Application to the Electron
In the case of a subatomic particle created by a vacuum fluctuation (or similar process) through the induction and stabilization of a vortex of supercurrent, Equation (2) describes the total trapped energy. Such value of energy is therefore identified as the rest energy of the particle, and provides a definition for the particle’s rest mass m:
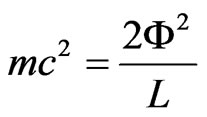 (3)
(3)
Such particle would be in dynamic equilibrium with the fields around it. Let’s start with the case of the “primordial” particle, the electron. One may explore the following property, first demonstrated by London [5] and later corrected by Josephson [6], that is, flux inside an open area bound by a superconductor region occurs in units n of the flux quantum Φ0 = h/(2e) in SI units. In the case of the electron one may pick n = 1, a single flux quantum. This might provide a criterion for a vortex reaching stabilization: that at least a single flux quantum be trapped. We then take Φ = nΦ0. This should apply also to large quantum numbers n, i.e., to the macroscopic loop of the SEO. Therefore, this model is based upon the hypothesis of flux quantization. No assumptions are made about the form and actual charge distributions in the particles.
The application of Equation (3) requires the value of L. The selfinductance L cannot be reliably obtained in this case by direct calculation from a current distribution since such distribution is unknown. The following approach is adopted: L must be based upon its definition as the ratio (Flux/current), with Flux an integer number of flux quanta, and the current being that “effective” current i that flowing round a circle of radius R will produce the particle’s measured magnetic moment μ. Note that R is actually the size of the region where the magnetic flux is confined, and is not in principle expected to represent the size of the region where mass is concentrated. With this definition for L and adopting Equation (3), two measurable parameters are inserted in this phenomenological model, i.e., the mass of the particle, and its magnetic moment. The soundness of this model can therefore be readily evaluated. Therefore we define:
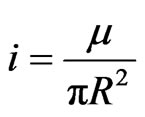 (4)
(4)
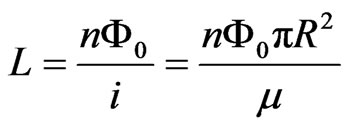 (5)
(5)
From Equation (3) one immediately obtains the following relation between the rest mass, the magnetic moment, and the radius, in terms of constants of Nature:
 (6)
(6)
which can be written as the following quantization rule:
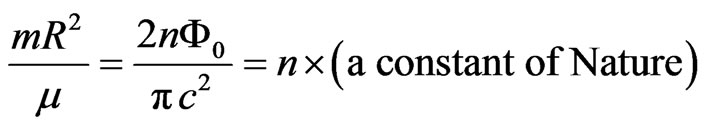 (7)
(7)
The constant in Equation (7) is 1.462 × 10−32 in SI units.
In the case of the electron, take m = 9.11 × 10−31 kg, μ = 9.274 × 10−24 J/T, n = 1, and Φ0 = 2.07 × 10−15 Wb. One obtains R = 3.86 × 10−13 m. In [7], this exact value is mentioned for a QED calculation of the size of a bound electron, and coincides with its Compton wavelength divided by 2π. According to the present model such size might be considered as a magnetic radius for the particle. The size of the region where mass should be concentrated is obtained from scattering experiments and is recognized as much smaller, in the 10−3 fm range [7]. Such result can be understood on the grounds that although magnetic energy is spread over a wide region occupied by flux (µ R3), the kind of experiment that produces very small dimensions may be probing the very short range of vibrations of the entire vortex, like in scattering processes related to resistivity in metals, and such small amplitude is associated with the actual “location” of mass.
3.2. Application of the Model to the Muon, to the Proton, and to the Neutron
The muon is considered as a massive electron (both are leptons), and even the muonic hydrogen atom has become an experimental tool in the study of the proton structure [8]. We have carried out a calculation of the muon magnetic radius, in the same spirit of the previous calculation for the electron. In this case, m = 1.88 × 10−28 kg, and the absolute value for its magnetic moment is μ = 4.49 × 10−26 J/T. The decay process of a muon results in an electron, a neutrino, and an antineutrino. If the total flux associated with the neutrino-antiparticle pair is taken as zero, and if one takes for the muon the same number n = 1 adopted for the electron, the number of flux quanta is conserved in the decay. Therefore, from Equation (7) the model’s magnetic radius of the muon is 1.9 fm, which is about twice as large as the proton’s measured radius [8]. This result coincides with the Compton wavelength for the muon divided by 2π like in the electron calculation. Similar to the electron, the muon should have its mass concentrated in a much smaller region [9].
The proton and the neutron are baryons. They are analyzed together in view of their similar structures based on an assembly of subparticles (which would be upand down-quarks). For the proton we take Equation (7) with m = 1.67 × 10−27 kg, and μ = 1.41 × 10−26 J/T. If one assumes R = 0.86 fm, close to the particle radius 0.84 fm recently obtained experimentally [8] (we are admitting that this radius represents the size of the region occupied by mass in this case, as well as the region occupied by flux), one obtains exactly n = 6. Such n > 1 might be regarded as a consequence of the proton being built from an assembly of subparticles. The neutron can be analyzed in a similar way. The mass of a neutron is only 0.14% greater than the proton’s, and the absolute value for μ-(neutron) = 9.66 × 10−27 J/T. However, the size of the neutron has not been accurately determined. If we assume 0.84 fm for the neutron, Equation (7) yields n » 8. This is a reasonable result in view of the decay pattern of the neutron, which produces an electron, a proton, and a neutrino. Since the model is based upon the hypotheses of flux quantization and conservation, if one takes n = 1 for the neutrino (another lepton), the absolute values of n obtained for the proton and the neutron would make the number of flux quanta to be conserved in this decay process.
The uncertainty in the value for R (even for the proton) turns the exact match with theory rather accidental, but values between 1 and » 10 obtained for n lay within the correct expected range. Furthermore, n greater than 1 should be expected in view of the known internal structure of the proton and the neutron. The model therefore gives quite reasonable results for a whole set of stable and unstable particles, for which important experimental data are available, on the grounds of the simple hypotheses of flux quantization and conservation, and that mass results from trapped magnetodynamic energies.
4. Analysis and Conclusions
In this paper, the description of mass previously developed in terms of energy for an idealized linear springload system [1] was extended to provide a model for the origin of mass for the main subatomic particles. Particles are considered as vortices of resistanceless currents, in dynamic equilibrium with the surrounding fields. Following the results obtained for the large-scale superconducting loop of the SEO, femtometer-scale vortices should be able to store flux down to the limit of individual quanta. The hypotheses of flux quantization and conservation have been explored through the whole discussion. By imposing such criterion to the electron with a single flux quantum trapped by the particle, we arrive at the same magnetic radius obtained by QED calculations. The model can be applied to the muon, to the proton, and the neutron as well. A calculation of the magnetic radius of the muon is presented. In order to match the measured radius for the proton, we need a greater number of flux quanta trapped in the particle creation event. The same applies to the neutron. This can be tentatively understood by considering the internal structures of the proton and neutron, comprising subparticles of different charges and polarities.
This simple phenomenological model, based upon the hyphotesis of particles formed by vortices containing integer numbers of flux quanta, has also been able to associate with each other in a quantitative way a set of parameters for each particle, in the form of a new quantization rule. Mass and magnetic moment appear together in this quantization rule, which therefore associates these two quantities.
To sum up, according to this model what is called the “mass” of a particle is the result of magnetodynamic energy confined in vortex form in a region of space, in equilibrium with the fields around, and with the amount of flux trapped obeying the flux quantization conditions. However, the magnetic and kinetic parts of the total energy are apparently associated with different length scales in space, which reflects into the different experimentdependent “radii” for the electron discussed in detail in [7] and analyzed here in Section 3.1.
It is hoped that strict theoretical treatments of this same problem will eventually produce results consistent with this phenomenological approach.
REFERENCES
- O. F. Schilling, Journal of Electromagnetic Analysis and Applications, Vol. 5, 2013, pp. 91-95. doi:10.4236/jemaa.2013.53015
- O. F. Schilling, Brazilian Journal of Physics, Vol. 37, 2007, pp. 425-428. doi:10.1590/S0103-97332007000300013
- O. F. Schilling, Superconductor Science and Technology, Vol. 17, 2004, pp. L17-L20. doi:10.1088/0953-2048/17/3/L01
- M. Cirio, G. K. Brennen and J. Twamley, Physical Review Letters, Vol. 109, 2012, Article ID: 147206. doi:10.1103/PhysRevLett.109.147206
- F. London, “Superfluids,” Vol. 1, Wiley, New York, 1950.
- M. Tinkham, “Introduction to Superconductivity,” Krieger, Malabar, 1980.
- M. H. MacGregor, “The Enigmatic Electron,” Kluwer, Dordrecht, 1992.
- A. Antognini, et al., Science, Vol. 339, 2013, pp. 417- 420. doi:10.1126/science.1230016
- K. Nagamine, “Introductory Muon Science,” Cambridge UP, Cambridge, 2003. doi:10.1017/CBO9780511470776
Note Added in Proof
The objective of this NOTE is to justify theoretically the numbers n = 6 and n = 8 of flux quanta obtained in the fit of the model to the data for the proton and the neutron, respectively. Following the assumptions taken that particles are vortices of supercurrents, the theory of charged superfluids as presented by London [5] should be applicable in this case. One of the properties of such superfluid is that any of its elements should display vorticity in the presence of magnetic fields( resulting here from electromagnetic fluctuations from vacuum). That is, the rotational of the velocity vector is finite and directly proportional to the local magnetic field [5]. It can readily be demonstrated that as a result, an element of this fluid containing one electronic charge and characterized by an angular momentum component of Ñ/2 ( spin-1/2) should enclose an amount of magnetic flux equal to one flux quantum Φ0. Therefore, this justifies the assumption that n = 1 for the electron and for the muon. If the same calculations are carried out for particles with 2/3 and 1/3 of the electronic charge, i.e., for up and down-quarks that form the proton and the neutron, one obtains that these quarks should respectively be associated with 3/2 flux quanta, and 3 flux quanta. Assuming that the assemblage of these quarks forming the proton or the neutron conserves the total magnetic flux, from the known composition of these subatomic particles one immediately obtains that the proton should be associated with 2 × (3/2) + 3 = 6 flux quanta, and the neutron with 2 × 3 + (3/2) = 7.5 flux quanta. The agreement with the required n for the proton is obtained, while the value n = 8 makes theory agree with experiment for the neutron, for the realistic values for R assumed for both particles. The number 8 is consistent with the fact that only integer numbers of flux quanta should actually be observable. Therefore, the analysis presented in this NOTE substantially reinforces the conclusions of this work, by providing a firmer theoretical basis for the model, as well as successfully including the internal structures of the proton and the neutron in the calculations.

